基于Modelica的交流伺服控制系统建模与仿真

胡锦涛，陈 路，杨 浩，张宝坤，鲍丙瑞

（苏州同元软控信息技术有限公司，江苏 苏州 215123）

0 引言

随着电机制造技术、微电子技术、工业实践的迅速发展，以交流电机为控制对象的交流伺服系统已广泛应用于航空航天、电动汽车、工业机器人等高精度领域［1］。在交流伺服电机中，永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）省去了励磁线圈、滑环和电刷，具有转动惯量小、响应速度快、功率密度高等优点，已成为伺服系统的主流机型［2-5］。现代机电产品已呈现出机、电、液、热、控等不同领域子系统相结合的复杂特性，进行整体设计和分析时，不同领域的子系统间呈现出较强的耦合性，采用传统单领域仿真分析工具无法满足复杂系统的整体设计与分析，将多个单领域仿真工具联合使用也无法从根本上满足多领域耦合复杂系统的设计与分析需求。此外，实际工程中通常以采购配套交流伺服驱动产品为主，并未考虑系统自身进行建模，将不利于产品的计算机设计分析和数字化统一验证［6-7］。

在复杂系统建模时，不同领域内的元件可用相同形式的代数方程、微分方程等进行描述。以此为基础，多领域统一建模仿真技术将机、电、液、热、控等不同领域的模型封装为一个系统模型，以满足生产过程中多领域耦合仿真的需求［8-9］。Modelica 语言作为一种开放的、面向对象的、基于方程的多领域统一建模语言［10］，通过微分代数方程描述组件间的关系，无需对连接关系和求解序列进行解耦和推导，可显著提升设计效率［11-13］。MWORKS 作为一个基于Modelica 的多领域建模与仿真平台，由苏州同元软控信息技术有限公司设计与开发，在国内汽车、能源、航空、航天等领域内得到广泛应用［14-16］。

本文以交流伺服控制系统的主流机型—永磁同步电机为研究对象，在MWORKS 平台上建立基于Modelica 的PMSM 伺服控制系统仿真模型，为数控机床、风电变桨、雷达天线等系统的多领域建模与仿真、伺服驱动产品的数字化验证提供了一种新思路。

1 控制原理

1.1 数学模型

考虑到PMSM 伺服控制系统在三相静止坐标系下的数学模型存在非线性、强耦合、高阶等特点，不利于模型分析和求解，为了简化分析，忽略不计空间谐波、电机铁芯饱和损耗、涡流和磁滞损耗、齿槽、换相和电枢反应的影响，且三相定子绕组严格对称，在空间互差120°电角度。

此外，为了进一步简化PMSM 的数学模型，使其更便于控制，在两相同步旋转坐标系下建立PMSM 数学模型。其中，式（1）、式（2）为电压方程；式（3）为磁链方程；式（4）为转矩方程；式（5）为机械运动方程［17-18］。

在该坐标系下，电机模型得到有效简化和解耦合，便于设计PMSM 伺服控制器。其中，ud、uq分别为定子d 轴、q轴电压；id、iq分别为定子d 轴、q 轴电流；ψd、ψq分别为定子d轴、q轴磁链；Ld、Lq分别为定子绕组d轴、q轴电感；R为定子电阻；p为微分算子；np为极对数；J为转动惯量；ψf为永磁体磁链；Te、TL分别为电磁转矩和负载转矩；we、wm分别为电角速度和机械角速度；B为系统阻尼系数。

1.2 伺服控制

本文在PMSM 伺服控制系统设计方面，采用目前应用较为成熟的三环控制结构，基本环节包括电流控制系统、速度控制系统和位置控制系统，具体控制原理如图1所示。

Fig.1 Principle of PMSM servo control system图1 PMSM伺服控制系统原理

图1 由内至外依次为电流环、速度环和位置环［19-20］。其中，由于电流环与被控对象最近，其调节器参数对系统影响较大；速度环作为PMSM 伺服控制系统的重要组成部分，具有响应速度快、控制精度高和调速范围广等特点；位置环处于最外层，具有良好的定位跟踪精度和速度响应能力。具体实现过程中，经电流传感器测得三相定子电流，通过坐标变换后作为内层电流环的反馈信号输入，在基于转子磁场定向坐标系下，定子电流矢量被分解为励磁分量和转矩分量，二者相互垂直实现磁链和转矩的解耦控制。

位置传感器和速度计算模块分别测得PMSM 转子的位置信号和转速信号，作为位置环、速度环的反馈信号输入。位置环的输出信号由速度环处理，速度环的输出信号由电流环处理。电流环输出的两相旋转坐标系定子电压Ud、Uq经Park 逆变换后得到Uα、Uβ，然后通过空间矢量脉宽调制技术（Space Vector Pulse Width Modulation，SVPWM）对三相逆变器功率管的开关时序与脉宽大小进行控制，从而实现PMSM 的高精度伺服控制过程。

2 多领域统一建模

MWORKS 作为一个基于Modelica 的多领域统一建模仿真平台，在国内汽车、能源、航空、航天等领域已得到广泛应用［21-22］。平台中的可视化建模、物理单位推导与检查、多工程领域系统建模等功能，在基于Modelica 语言的工程建模解决方案的设计与验证过程中起着重要作用［23］。

根据PMSM 伺服系统的控制原理，本文借助多领域建模仿真平台—MWORKS，对系统进行基于Modelica 语言的多领域统一建模与仿真，整体架构如图2所示。

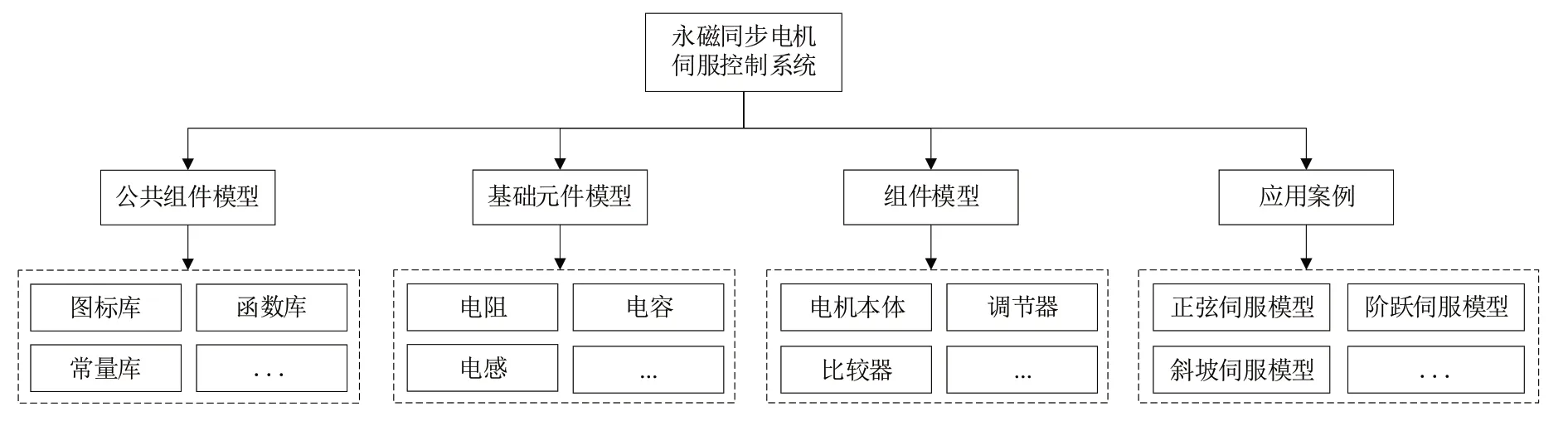
Fig.2 PMSM servo system model architecture图2 PMSM伺服系统模型架构

2.1 PMSM本体

在PMSM 伺服控制系统中，PMSM 本体作为控制对象，在MWORKS 平台中对其进行Modelica 建模。通过输入三相交流电，经过坐标变换、气隙模型中的机电转换等过程后输出机械能，电机本体模型图标与内部结构如图3所示。

Fig.3 PMSM body module图3 PMSM本体模块

2.2 逆变器

在设计逆变器时，本文采用三相全桥逆变器结构，如图4 所示。实际工作过程中，直流侧接入直流电源后，在系统三环控制作用下，上游SVPWM 模块输出一定占空比的开关信号至逆变器中，以有效控制各路开关的通断逻辑，从而控制三相逆变器模块输出目标电压矢量。

Fig.4 Inverter module图4 逆变器模块

2.3 SVPWM调制

在PMSM 伺服系统控制器中，采用SVPWM 技术对逆变器输出的电压矢量进行控制，以圆形旋转磁场为目标，最大限度追踪PMSM 的磁链轨迹，以达到转矩的最佳控制效果［24-25］，SVPWM 模块内部结构如图5所示。

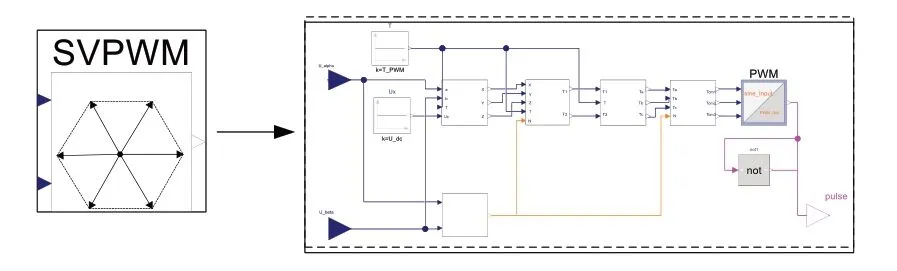
Fig.5 SVPWM module图5 SVPWM模块

在实际设计时，三相逆变器中的6 个功率管对应8 种开关状态，每一种状态对应一个基本的空间电压矢量，即为U0（000）、U1（001）、U2（010）、U3（011）、U4（100）、U5（101）、U6（110）和U7（111）。其中，U0（000）、U7（111）为两个零矢量。

为了使三相逆变器输出的实际磁通接近圆形，可将SVPWM 的8 个基本电压矢量划分为6 个扇区，如图6所示。

Fig.6 Voltage space-vector图6 电压空间矢量

2.3.1 扇区判断

在应用SVPWM 技术时，首先需要确定合成的电压矢量Us 所在的扇区，根据Uα、Uβ和扇区的关系可作如下变换：

式中：Uα、Uβ为电压矢量的α 轴、β 轴分量；Ua、Ub、Uc为中间变量。

通过判断中间变量极性，可得当前需要合成的电压矢量Us所在的扇区。令：

设N=A+2B+4C，通过N 值可快速确定扇区位置，对应关系如表1所示。

Table 1 Correspondence between sectors and N values表1 扇区与N值对应关系

2.3.2 电压矢量作用时间计算

设相邻空间电压矢量的作用时间分别为T1、T2，为了便于计算引入X、Y、Z中间变量，计算公式为：

式中：Udc为三相逆变器的直流侧电压；Uα、Uβ分别为电压矢量的α 轴、β 轴分量；T为PWM 调制周期。

不同扇区T1、T2与X、Y、Z的对应关系如表2所示。

Table 2 Time of voltage vector action表2 电压矢量作用时间

2.3.3 电压矢量切换点计算

根据确定的扇区和计算的电压矢量作用时间，将其转化为三相逆变器中各个开关管的切换时刻，引入3 个时间变量Ta、Tb、Tc，具体计算公式为：

设不同扇区内电压矢量切换点依次为Taon、Tbon、Tcon，与Ta、Tb、Tc的对应关系如表3 所示。最后，利用周期为T、幅值为T/2 的等腰三角波与各个切换点的位置信号进行比较，得到三相逆变器中各开关管的实际控制信号。

Table 3 Sector and voltage vector switching point表3 扇区与电压矢量切换点

3 仿真与验证

在MWORKS 平台搭建基于Modelica 的PMSM 伺服控制系统仿真模型，如图7 所示。电机的主要参数为额定电压38 V，额定频率50 Hz，定子电阻1.05 Ω，极对数1，d轴电感0.7 mH，q 轴电感为0.7 mH，漏感0.01 mH。为了满足工业场景中的跟踪控制需求，PMSM 伺服控制系统需要满足各类工况中目标转速或位置跟随性能。

Fig.7 Modelica model of PMSM servo control system图7 PMSM伺服控制系统Modelica模型

3.1 位置环仿真

PMSM 伺服控制常用于雷达天线、风电变桨、飞行器姿态调整等高精度位置控制的场景中，为此本文在MWORKS 平台中对系统模型进行了3 种典型工况的位置控制测试，仿真结果如图8—图10 所示。通过模拟恒值信号、分段斜坡信号和正弦信号的变化过程，证明了PMSM伺服系统的跟随效果好，误差均小于0.5%，能满足工业场景的应用需求。

Fig.8 Result of position loop following in condition 1图8 工况1位置环跟随结果

Fig.9 Result of position loop following in condition 2图9 工况2位置环跟随结果

Fig.10 Result of position loop following in condition 3图10 工况3位置环跟随结果

3.2 速度环仿真

除了工业场景中的位置控制外，转速控制需求较为常见，例如医疗设备、压缩机、飞机发动机等系统。在MWORKS 平台中对系统模型进行3 种典型工况的速度控制测试，仿真结果如图11—图13 所示。通过模拟恒值信号、分段斜坡信号和正弦信号的变化过程，证明了PMSM伺服系统的跟随效果好，误差均小于0.5%，能满足工业场景的应用需求。

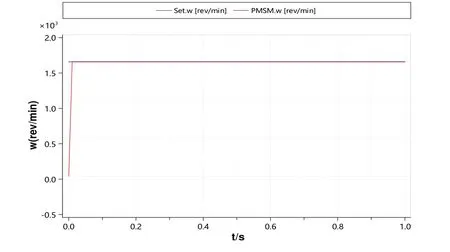
Fig.11 Result of speed loop following in condition 1图11 工况1速度环跟随结果

Fig.12 Result of speed loop following in Condition 2图12 工况2速度环跟随结果

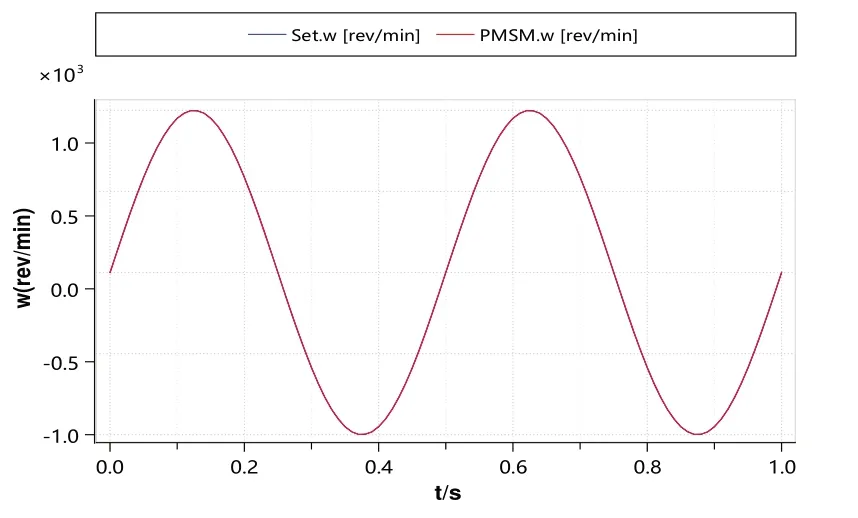
Fig.13 Result of speed loop following in condition 3图13 工况3速度环跟随结果

4 结语

本文通过分析PMSM 伺服控制系统的基本组成和工作原理，借助多领域建模仿真平台MWORKS 构建了基于Modelica 的PMSM 伺服系统仿真模型，并测试了位置控制、速度控制的多种典型工况。

结果表明，基于Modelica 的PMSM 伺服控制系统模型动态特性好，跟随误差均小于0.5%，能较好地模拟实际工况应用过程，可为后续雷达跟踪、飞行器姿态控制、数控机床等系统仿真提供建模基础，也可为机械、电气、液压、控制等多专业融合复杂系统的仿真建模与伺服驱动产品的数字化验证提供参考。