加载系统迭代学习控制器设计与控制算法研究

李沛辙，白国振

（上海理工大学 机械工程学院，上海 200082）

0 引言

随着科学技术的大力发展，国防军工、汽车制造、航空航天等领域，对于某些重要零件的性能要求越来越严格，可以模拟真实工作环境的加载系统应用也越来越广泛［1-2］。加载系统在工程上通常被称为负载模拟器，是指在实验室等非真实环境下对被测零件进行模拟性负载测试的实验设备［3］。加载系统分为多种，主要包括磁粉加载系统、电液伺服加载系统、气动加载系统、电动伺服加载系统［4-5］等。

根据近年来研究论文可以看出，电动伺服加载是现阶段研究的重点，但电动伺服加载的控制难度很高［6-8］。为了更好地对电动伺服系统进行控制，学者们提出了多种控制算法，主要有滑模算法以及PID（Proportion Integration Differentiation）控制算法。随着智能控制和计算机技术的发展，智能控制算法与传统算法结合应用的场合越来越多［9］。

人类自出生以来对世界的认知就是通过反复学习来完成的，学习在认知过程起到十分重要的作用。根据这一学习方法，工程控制领域诞生了智能控制的分支——学习控制。日本学者Uchiyama［10］最先提出了迭代学习控制理论，经过众多学者的研究，迭代学习在理论和应用上都有了新的进展和突破［11-12］。近些年学者开始将迭代学习与其他算法进行结合，例如黄文文等［13］设计了一种学习增益在线自适应调节的P 型迭代学习控制策略，加快了超声波电机转速控制的收敛速度，但是在自适应的调整方面还是依据实测数据给出，不具备自适应算法的普适应；何焯毅［14］将迭代学习算法应用于永磁同步电机中，并且通过实验证明了迭代学习算法对永磁同步电机控制的有效性，但是缺乏与其他算法的结合，迭代学习的次数较多；殷春武［15］将滑模控制和迭代学习做了有效结合，增强了迭代学习控制器的鲁棒性，但是对数学模型要求较高，失去了迭代学习不依赖数学模型的优点。

本文从改善电动伺服加载效果的目的入手，结合电动伺服加载系统的周期性特点，设计了一种基于模糊控制的迭代学习控制器，能够在保留迭代学习优越控制效果的同时大大减少迭代次数，弥补迭代学习算法学习迭代次数多的缺点，使其更快地达到所指定的扭矩曲线。同时，其不依赖系统自身的参数，实现效果好。本文的创新性在于将模糊控制与迭代学习控制器结合，能够自适应调整学习律的增益，能够加快收敛速度，减少收敛次数，并且很好地应用于电动伺服加载系统中，取得了较好的扭矩曲线跟踪效果，并且保留了迭代学习控制器不依赖数学模型这一优点。

1 迭代学习控制器

1.1 迭代学习概论

迭代学习控制的原理为：在期望轨迹周期时间段［0，T］中，期望轨迹yd(t)已知。通过迭代学习寻找合适的离散化输入控制u(t)，使得系统输出y(t)在区间［0，T］上对期望轨迹的跟踪达到较好的控制效果。迭代学习关键在于通过迭代的方法寻找合适的输入，将输出的误差用于构建输入控制信号的学习律，经过迭代，生成收敛于u(t)的函数序列{uk(t)}。学习律的形式如（1）、（2）所示：

式中：k=0，1，2，3…为迭代次数。

迭代学习算法的流程图如图1所示。

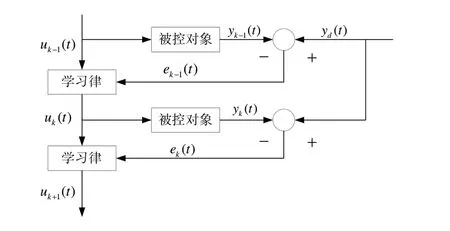
Fig.1 Algorithm flow chart of iterative learning图1 迭代学习算法流程

迭代学习的学习律可以采用PID 控制、神经网络、自抗扰控制等控制理论，从而实现迭代学习与其他控制方法的融合，更好地推动控制理论的发展。

1.2 迭代学习控制的特点

迭代学习在具有重复性被控对象的控制系统中应用较为广泛，其并不依赖于被控系统数学模型的建立，可以简化或者省略被控系统的参数辨识估计等复杂繁琐的计算。

迭代学习控制是在时间轴t和离散轴k两个轴同时进行的，t和k轴具有完全的相关性，可以说k就是t的离散形式。

假设非线性系统如（3）、（4）所示：

式中：k为迭代循环次数。迭代学习特性如下：①迭代学习控制最终目的是得到期望的输出，并不依赖数学模型；②被控系统的期望输出具有周期性，每次时间间隔为周期T；③被控系统期望输出yd(t)是给定的已知量，且为关于时间t的函数；④被控系统每次迭代运行的输出yd(t)可测量，误差信号可求得；⑤被控系统的结构不变；⑥被控系统迭代时初始状态应在期望轨迹上；⑦被控系统控制量uk+1(t)的递进规律满足式（5）。

迭代学习控制适用于满足以上要求的系统，经过有限次迭代可以达到较好的控制效果。

1.3 迭代学习控制器设计

电动伺服加载系统是由负载电机和加载电机经过连接件连接的被动加载系统。对于电动伺服加载系统而言，一般给定一个周期性的控制信号，对测试部件进行扭矩疲劳测试实验，所以迭代学习控制在电动伺服加载系统中较为适用。

加载系统的控制结构框图如图2所示。

Fig.2 Control structure block diagram of loading system图2 加载系统的控制结构框图

由加载系统的结构可知，控制算法主要由加载电机的扭矩控制。为了实现更好的控制效果，设计PD 形学习律的迭代学习控制器，迭代公式如式（6）、（7）所示：

式中，KP，KD为比例微分系数；ek为输出误差；N为一个周期内的总序列数。

在实际的实验中发现，在迭代到一定程度时，输出的轨迹已经实现了对输入控制的跟随，但此时迭代学习依旧在进行迭代，对下一次的控制进行修正，最终迭代学习会产生发散问题，导致迭代学习控制的失效。此时控制失效与学习律PD 值没有关系，PD 值的大小只与达到发散的时间点长短有关，控制失效的状态表现为扭矩的发散，发散情况如图3所示。

Fig.3 Divergence of loading torque based on iterative learning algorithm图3 迭代学习算法加载扭矩的发散

迭代学习的数学推导证明迭代学习算法是收敛的，但是控制系统的滞后现象导致了收敛条件的破坏。为了解决这一问题，引入均方根误差，解决了无限次迭代产生的超调发散现象。均方根误差的计算公式如式（8）所示：

迭代学习的一个重要指标是迭代次数，在输出轨迹稳定不发散的前提下，为更好地优化迭代学习控制器的性能，设计了改进的迭代学习控制器。

2 改进迭代学习控制器

为了减少迭代次数，需要一种合适的算法来优化迭代学习控制器。模糊控制算法一般根据专家经验对控制对象进行处理，不依赖于控制系统的数学模型，能有效地对控制输出作出合理的响应。模糊控制具有自适应功能，能够根据反馈调节输出参数，具有速度快、稳定性好的优点［16-18］，所以本文将模糊控制与迭代学习相结合，设计了二维模糊控制器对迭代学习的学习律参数进行优化。

模糊控制是通过设定的模糊规则来进行控制量的在线规划与调整。除了单一的模糊控制以外，模糊控制常与PID控制结合，模糊PID控制器也被应用于扭矩加载系统中，能够通过模糊控制在线调试PID 的比例、积分、微分参数，使得力矩跟踪的响应速度得到明显提高，也对非线性和不确定因素起到了更好的控制效果。但是模糊控制PID 也有缺点，其控制精度较低，对稳态误差的消除效果较差。本文采用模糊控制与迭代学习相结合的形式，既优化了模糊控制精度低的问题，又改善了迭代学习迭代速度慢的问题。

模糊控制系统将被控对象的输出值与系统给定的输入值进行对比得到误差信号，将误差信号作为模糊控制器的输入值，输入值经过隶属度函数进行模糊化处理，隶属度函数主要有高斯型、三角型、S 型等。根据模糊规则进行模糊关系的推理，最后再进行模糊输出。将控制量施加到被控对象上，实现模糊控制。

模糊控制器的结构主要包括论域的设计、输入变量的模糊化、模糊规则的设计和模糊输出。

本文设计的模糊控制器为二维，选取误差e和误差变化率ec两个输入。因为迭代学习的参数并非实时变化，所以本文采取误差以及误差变化率在周期内绝对值的平均值作为模糊控制器的输入参数，如式（9）、（10）所示。

模糊输出的方法采用重心法来进行反模糊，迭代次数的多少主要与学习律的KP值有关，所以取ΔKp为模糊输出变量，此时模糊控制后的学习律输出参数为式（11）。

在每次周期性输出结束时进行PD 学习律参数KP的自动调整。图4为模糊控制原理框图。

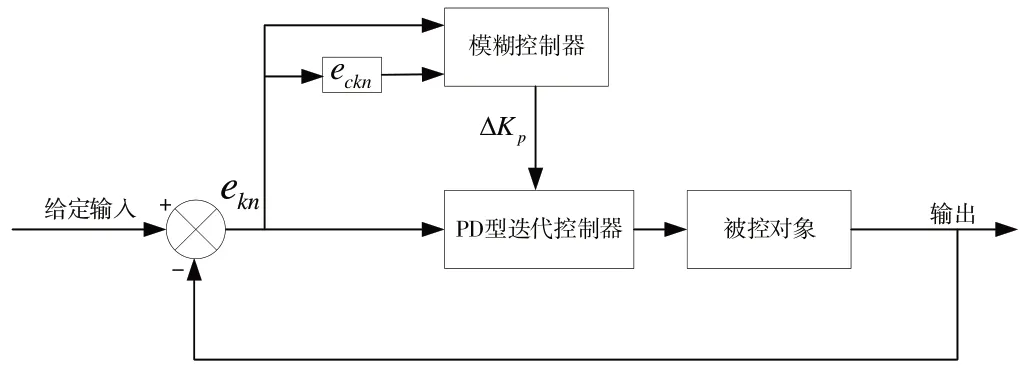
Fig.4 Principle block diagram of fuzzy control图4 模糊控制原理框图

输入变量和输出变量分为7 部分，分别为NB、NM、NS、ZO、PS、PM、PB。ekn的取值范围为［-0.5，0.5］，eckn的取值范围为［-0.005，0.005］，ΔKp的取值范围为［-10，10］。本文选取三角隶属度函数。

针对电动伺服加载系统对响应要求高，且迭代学习算法迭代速度慢的特点，设计可以在误差较大时加快迭代速度、减少迭代次数的模糊规则。最终ΔKp的模糊控制规则见表1。

Table 1 Fuzzy control rule of ΔKp表1 ΔKp的模糊控制规则

加入模糊控制后，在迭代学习的初期误差较大时，模糊控制会增加学习律的KP值，以加快响应，减少迭代次数。同时在误差较小时减少KP的值，防止产生超调，使加载系统的扭矩控制精度更高。

3 实验平台搭建与实验验证

3.1 实验平台搭建

本试验台的搭建目的是完成高精度的扭矩跟随，并且对本文提出的改进迭代学习控制器进行验证。图5 为加载实验台框架，图6 为实验平台控制系统结构。整个实验台包括控制部分、执行部分、测量部分、连接部分。

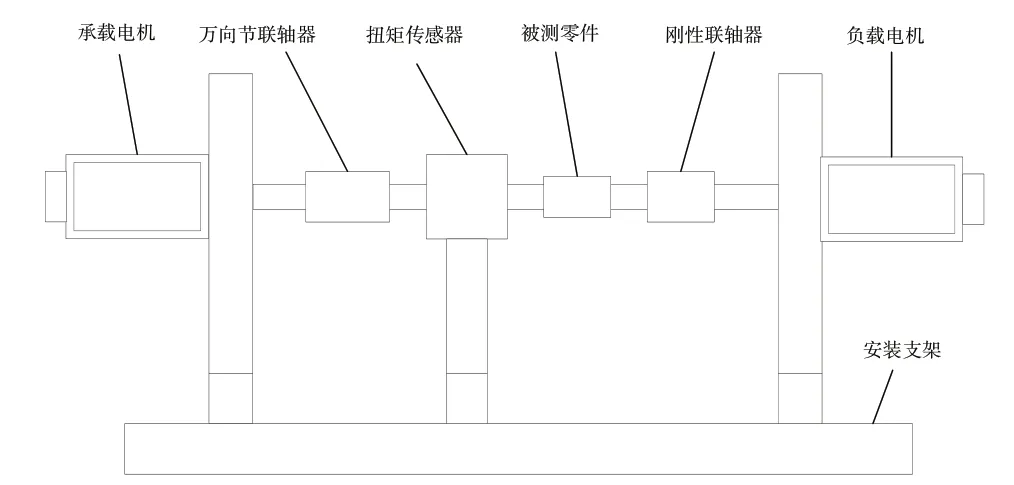
Fig.5 Loading test bench frame图5 加载实验台框架

3.1.1 控制部分

工控机是加载平台的信息处理部分，负责系统的整体运动控制、信号采集和图形化数据。选用倍福公司的C6920-0040，此工控机结构紧凑，实时性较高，能够进行毫秒级运算和控制。数字IO 采用倍福公司的E-BUS 耦合器和EtherCATI/O 端子模块，耦合器功能为连接EtherCAT 和EtherCATI/O 端子模块，通过以太网进行数据通信。软件层面采用倍福公司的Twincat3 软件平台，使用ST 语言进行高级语言编程，实现算法。

3.1.2 执行部分

根据实验台的要求，执行部分主要由加载端电机和驱动端电机构成。位置电机为松下伺服电机，其型号为MSMF012L1U2M，对应的驱动器型号为MSMF012L1U2M。其响应频率高，适用于高精度、高频率的工作环境。通过以太网与控制器进行通讯，实现电机的运动控制。加载电机为三菱伺服电机，其型号为HG-KR43J，对应的驱动器型号为MR-J4-40A。负载电机自带高分辨率编码器，可以实现高精度、高速度转动。负载电机通过倍福模块进行连接，根据模拟量进行扭矩控制。

3.1.3 测量部分

本试验台采用扭矩加载试验台。在试验过程中，由于电机长时间高速运转，常规的接触式扭矩传感器无法满足试验要求，因此本文选用DYN-200号传感器。

3.1.4 连接部分

联轴器是加载系统中必不可少的连接件，能够进行扭矩的传递，还能起到减震和缓冲的作用。为了得到更好的试验台性能，选取刚性联轴器和万向节联轴器，刚性联轴器的刚度大，对扭矩的传递响应比较迅速，传递精度也更好；万向节联轴器的传递精度高，并且具有克服偏心的作用，能够很好地弥补安装时造成的同轴度误差。

加载实验平台实物为图7所示。

Fig.7 Loading test bench图7 加载实验平台

3.2 实验验证

在倍福工控机上采用ST 语言实现控制算法，利用Twincat3 的scope 功能对输出扭矩进行波形输出，以验证本文控制算法的性能。图8—图10 和图11 分别是普通PID、模糊PID、迭代学习和改进迭代学习控制器输出的扭矩曲线。

Fig.8 General PID control output curve图8 普通PID控制输出曲线

判断一个加载系统好坏的评价指标主要由扭矩加载的幅值误差和相位误差两部分组成。幅值误差是指扭矩给定值和扭矩输出值的误差，本文采用峰值误差来近似幅值误差；相位误差是指扭矩给定值的相位和扭矩输出值的相位之间的误差。从图8 可以看出普通PID 加载的幅值误差和相位误差均较大，精度较低，达不到高精度的加载要求。图9 的模糊PID 加载相比于普通PID 加载能够有效缩小幅值误差和相位误差。由图10 可以看出在经过6 次迭代学习以后，加载的幅值误差和相位误差均远远小于模糊PID 加载。图11 可以看出经过3 次迭代学习以后，加载的幅值误差和相位误差更小。

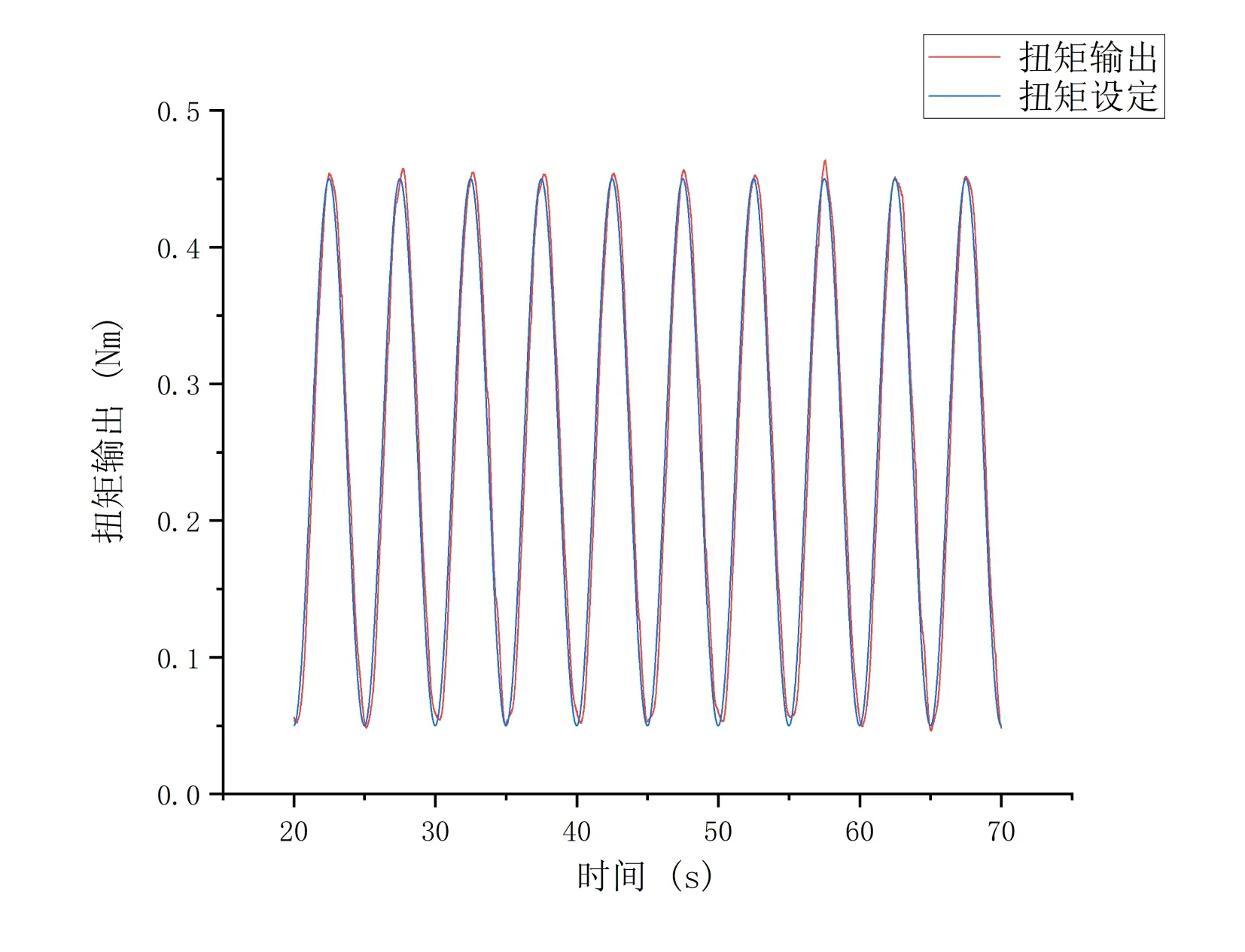
Fig.9 Fuzzy PID control output curve图9 模糊PID控制输出曲线

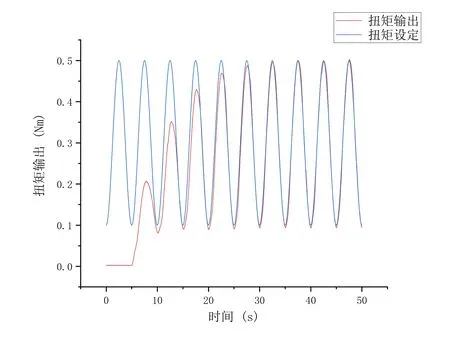
Fig.10 Iterative learning control output curve图10 迭代学习控制输出曲线

Fig.11 Improved iterative learning control output curve图11 改进迭代学习控制输出曲线

表2 为4 种控制算法的性能比较结果。一般的工程误差适用条件为5%，其中普通PID 加载的幅值误差和相位误差均超过了工程适用条件，分别为7.25%和6.06%。模糊PID 加载相较普通PID 加载有了很大改善，幅值误差为2%，相位误差为3.02%，已经可以满足一般的工程需要。迭代学习加载经过6 次迭代后，幅值误差为1%，相位误差为1.28%。而模糊迭代学习加载经过3 次迭代后，幅值误差为0.5%，相位误差为1.26%。

Table 2 Performance comparison of 4 control algorithms表2 4种控制算法的性能比较

根据实验结果可以看出，ST 语言可以很好地对算法进行实现。通过实验台的加载，普通迭代学习控制器在第6次迭代才达到一个较好的输出曲线，而本文设计的基于模糊控制的迭代学习控制器在第3 次迭代时已经达到了一个较好的输出曲线。通过与普通PID 和模糊PID 控制器对比得出结论，基于模糊控制的迭代学习加载跟踪精度最高，在有限次迭代学习后能够很好地跟踪输入曲线，具有跟踪效果好的优点，能够很好地解决电动伺服加载系统加载的扭矩跟随问题，并且基于模糊控制的迭代学习控制器还具有模糊控制自适应的特点，能够用更少的迭代次数更快地获取所需要的跟随扭矩曲线。

4 结语

本文以电动伺服加载系统控制出发，选择迭代学习控制器为优化对象。迭代学习的优点是跟踪轨迹良好，并且不依赖控制系统的数学模型，能够方便地实现算法，具有计算量小控制效果好的优点，但是迭代学习的迭代次数一般较多，响应较慢。迭代次数一般与学习律的取值有关，所以针对迭代学习迭代时间慢的问题，本文设计了一种基于模糊控制的迭代学习控制器，能够极大地减少迭代学习控制器的迭代次数，取得了较好的扭矩跟随效果，具有较高的工程实用价值。

本控制算法虽然不依赖数学模型，但是在一些基本参数上仍需要根据实际控制对象进行微调。未来研究将以自动寻找最优参数为重点，尝试自动根据反馈数据找到合适的学习律参数，实现整个控制器的自动化设置。