S-E-MBR：一种基于E-MBR码的分布式存储系统扩容方法

黎 聪，唐 聃

（1.成都信息工程大学 软件工程学院；2.四川省信息化应用支撑软件工程技术研究中心，四川 成都 610225）

0 引言

随着人工智能、物联网、云计算等计算机技术的逐渐成熟，数据量级呈爆炸式膨胀［1］。分布式存储系统因其底层硬件结构和文件系统可以灵活扩展而被人们青睐，常用于解决大数据难题。然而，更多的存储设备为系统带来了更大的数据丢失风险。为保证数据的可靠性与可用性，分布式存储系统需要构建相应的容错策略［2-3］。普通集群使用多副本技术构建容错策略，其实现过程简单，但集群空间消耗大［4-5］。而纠删码技术通过特定算法计算冗余块进行容错，虽然编译码计算复杂度较高，但其存储利用率和灵活性高，被越来越多的分布式系统使用［6］。例如，分布式文件系统Ceph 就引入了Jerasure 库、ISA-L 库（Intelligent Storage Acceleration Library）等纠删码编码和解码库［7］。但一些经典纠删码，如RS 码（Reed-Solomon Codes），在数据修复过程中译码所需数据量往往是丢失量的数倍，会占用大量网络传输带宽和磁盘I/O（Input/Output）资源，造成集群资源的浪费［8］。E-MBR 码（Exact Minimum Bandwidth Regeneration Codes）在一定程度上解决了该问题，其通过引入网络编码的概念，在节点修复时选取较多节点参与修复过程，且参与修复的节点首先对本节点内的数据进行线性组合后再上传，极大减少了修复失效节点的带宽消耗［9］。

由于电子商务、Web 服务和金融等行业的特殊性，需要对数据进行实时访问，使得数据中心必须为用户提供7×24h 的高质量响应服务，然而数据迁移量和扩容时间等因素均会影响扩容效率，造成响应延时［10］。因此，如何使用更短的时间、更少的传输数据量完成扩容成为难点所在，也受到了越来越多科研人员的关注。目前，许多研究在特定的RAID-6（Redundant Arrays of Independent Disks）编码上实现了扩容［11-15］。例如，文献［11］对数据迁移和奇偶校验数据更新过程进行了优化，减少了扩容时间，但只适用于离线场景且平均响应时间未减少；文献［12］通过将旧硬盘中的部分数据块迁移到新硬盘中实现了最小成本的数据迁移，但未说明响应时间变化和适用场景；文献［13］改变了数据迁移方式，使得数据块只在同一行奇偶链中移动，从而达到了数据迁移最小值，但其同样未说明响应时间变化，且只适用于离线场景。文献［16-19］在再生码［9，20］的基础上实现了扩容，其中文献［16-18］均证明了最小扩容带宽，但文献［16］只有在功能性修复的情况下可以达到，文献［17］需要扩容前后重构节点数相等（k=k'）时才能达到，而文献［18］的方法复杂度较高，实现困难；文献［19］提出两种扩容方法，但其实现方法存在特殊性，未能达到最小扩容带宽下限。此外，文献［21］提出的Round-Robin（RR）扩容方法是公认数据布局最优的方法，该方法适用范围广，但其扩容时几乎需要迁移所有数据块，因此数据迁移量和扩容开销最大，扩容时间较长；文献［22］基于RS 码提出转置数据布局，实现了Scale-RS 扩容方法，该方法达到了数据迁移量的下限，从读取并行性和写入吞吐量方面提高了存储集群的I/O 性能，但未能达到校验更新的开销下限。

目前国内外扩容方法分数据迁移与校验更新两步完成，大多数不适用或未说明是否适用于在线场景，且部分扩容方法未能达到最优下限，或只有在特殊参数条件下才能达到，限制了扩容方法在在线场景中的应用。随着再生码在分布式场景中的广泛使用，以及在线场景存在的必要性不断增加，不可避免地需要使用在线扩容方法缓解存储和计算压力，提高分布式存储系统性能。为此，本文提出一种基于E-MBR 码的扩容方法S-E-MBR，可满足在线扩容场景需求，解决了使用E-MBR 码作为容错策略的分布式存储系统的存储瓶颈问题。

1 S-E-MBR扩容方法

S-E-MBR 方法结合了E-MBR 码的构造特点与在线更新时数据从外部输入的特点，使用增量更新［23］和RS 码生成矩阵动态扩张［24］的思想，省去了数据迁移过程，从而能最大程度地减少扩容时的开销。

1.1 E-MBR码构造

记E-MBR 码的总节点数、重构节点数、单节点修复所需节点数和扩容节点数分别为n、k、d和s，底层RS 码总编码块和原始数据块分别为θ和B。图1（彩图扫OSID 码可见，下同）为E-MBR 码(n=4，k=2，d=3)的构造示意图，代表总节点数使用基于范德蒙矩阵的RS 码(θ=d(d+1)/2=6，B=kd-k(k-1)/2=5) 对原有原始数据块vi(1 ≤i≤5)进行编码，得到编码块vi(1 ≤i≤6)。其中，vi(1 ≤i≤5)为数据块，v6为校验块或冗余块。将编码块与图1 中的θ=6 条边一一对应，对于每个存储节点，只存储与其相连的d=3条边所对应的编码块，则编码完成。

Fig.1 Schematic diagram of E-MBR codes（n=4，k=3，d=2）encoding process图1 E-MBR码(n=4，k=2，d=3)构造示意图

1.2 增量更新

在E-MBR 码中，底层使用基于范德蒙矩阵的RS 码对原始数据块进行编码，其生成矩阵的动态扩展机制能够快速实现校验更新。记q为(n，k)RS 码扩容的节点数，当其扩容时，容错数r=n-k不发生变化，其生成矩阵变化表示为：

在RS 码扩容时，生成矩阵由k×k阶单位矩阵Ik与r×k阶的范德蒙矩阵Vr，k扩容为(k+s) × (k+s)单位矩阵Ik+s与r× (k+q)范德蒙矩阵Vr，k+q。采用pi(1 ≤i≤r)表示原始校验块，di(1 ≤i≤k) 表示原始数据块，(k+1 ≤i≤k+q)表示新增数据块，则扩容后的新校验块(1 ≤i≤r)可由式（2）得到，校验更新完成。

1.3 S-E-MBR扩容方法详细设计

S-E-MBR 扩容方法分为数据填充与校验更新两步完成。填充数据来源于外部输入。由于S-E-MBR 扩容时不需要将条带分组，只需以(n，k，d，s)一个条带扩容过程为例进行说明，其余条带操作均相同。

1.3.1 数据填充

记M为n×θ的矩阵，代表全连通无向图的关联矩阵，其中(i，j)=1 表 示Vj需 要放置在nodei。关联矩阵M的构造方式为递增式扩张，即每次扩容1 个节点，经过s次扩容即可得到最终需要的(n+s，k+s，d+s)E-MBR 码的关联矩阵M'。根据M'进行数据填充，对于同一节点的数据可以使用聚合式发送，能够最大程度地减少其I/O 次数。

定理1：扩容前M每行有且仅有d个1存在，扩容s个节点后M'每行有且仅有d+s个1存在。

证明：记θ'为扩容后对应的参数，扩容前后容错数r=d-k=d'-k'不发生改变，因此扩容后θ'=d'(d'+1)/2。首先可以得到扩容前M每行有且仅有d个1 存在。若s=1，可以得到M'需要新增的部分为(n+1) × (θ'-θ)，记为Q。由于Q由n× (θ'-θ)的单位矩阵与1 × (θ'-θ)的1矩阵构成，其每行有且仅有1 个1，每次扩容1个节点时，其每行也只增加1 个1。当s＞1 时，只需重复上述过程s次，增加s个1，因此M'每行有且仅有d+s个1存在，证毕。

定理2：扩容前后M'每列有且仅有2个1存在。

证明：扩容前M每列有且仅有2 个1 存在，若s=1，新增部分Q由n× (θ'-θ)的单位矩阵与1 × (θ'-θ)的1 矩阵构成，每列有且仅有2 个1，不影响扩容前的M。因此，当重复上述过程，经过s次扩容后，M'依然每行有且仅有2个1存在，证毕。

以上定理的证明表明扩容前后E-MBR 码本身的构造特点未发生改变，即扩容方法并不会对编码过程产生影响，这是扩容方法应遵循的标准。

下面以S-E-MBR 扩容方法一次性扩容2 个节点为例进行说明。图2 为(n=5，k=3，d=4)时的关联矩阵示意图，方框分别表示从(n=3，k=1，d=2)开始，每增加一个节点，M的增加部分Q。虚线部分表示每次进行聚合发送的部分，首先将得到的新增数据分为新增数据块vi(4 ≤i≤10)；然后将{v4，v7}、{v5，v8}、{v6，v9}分别聚合发送到原始节 点nodei(1 ≤i≤3) 中；最后将{v4，v5，v6，v10} 与{v7，v8，v9，v10}分别聚合发送至新增节点nodei(4 ≤i≤5)中即可完成数据填充。

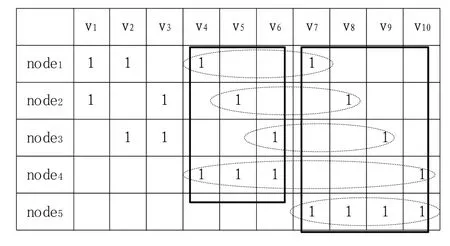
Fig.2 Schematic diagram of correlation matrix when n=5，k=3，d=4图2 参数为n=5，k=3，d=4时的关联矩阵示意图

1.3.2 校验更新

校验更新阶段同样采用“1.2”小节直接增量更新的方法，首先直接计算出更新所需增量块，然后将其发送至校验块进行更新即可。同样以(n=3，k=1，d=2，s=2)为例，扩容前E-MBR 码使用(n=3，k=2)RS 作为底层编码方法，因此{v1，v2}为数据块，v3为校验块。扩容后E-MBR需要使用(n=10，k=9)RS 码作为编码方法，因此q=7，校验块由式（3）得到。只需要将增量Δv3分别发送至校验块v3即可完成更新。至此，一个条带的扩容过程完成。

1.4 S-E-MBR扩容方法示例

由于“1.3”小节已经对扩容2 个节点的情况进行了说明，为证明S-E-MBR 扩容方法的普适性，以下对扩容1 个节点的详细过程进行举例说明。为便于描述，记四元组(n，k，d，s)表示E-MBR 码从参数(n，k，d)扩容到参数(n+s，k+s，d+s)。图3为使用S-E-MBR 方法从参数(n=4，k=2，d=3)扩容到(n=5，k=3，d=4)时的示意图。

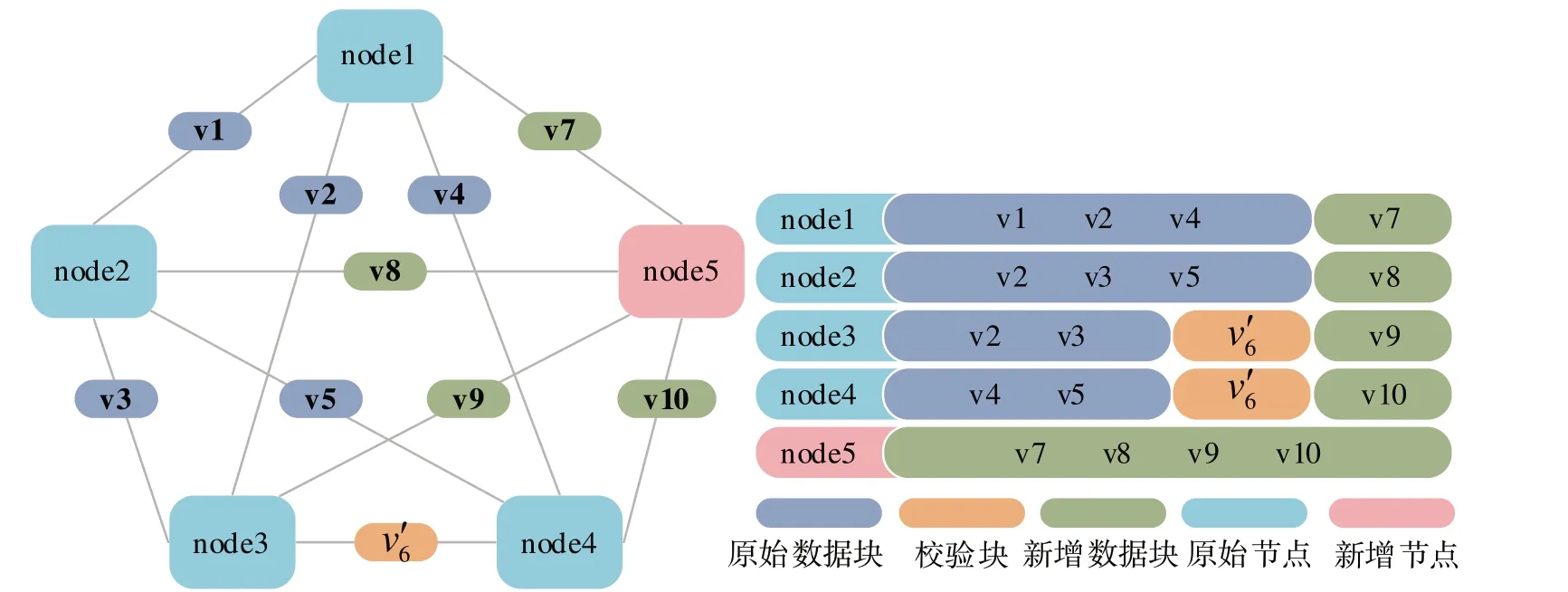
Fig.3 Schematic diagram of expanding one node using S-E-MBR method图3 S-E-MBR方法扩容1个节点示意图

使用S-E-MBR 方法扩容1 个节点分数据填充与校验更新两步完成，过程如下：

（1）数据填充。填充过程可以分为原始节点填充与新增节点填充两种。在原始节点nodei(1 ≤i≤4)中，只需要将新增数据块vi(7 ≤i≤10)分别发送到对应节点即可；在新增节点node5中，则需要先将新增数据块vi(7 ≤i≤10)打包，然后再放入到新增节点node5中。

（2）校验更新。当E-MBR 码从(n=4，k=2，d=3)扩容到(n=5，k=3，d=4)时，RS 码需要从(n=6，k=5)扩展到(n=10，k=9)，此时q=4，根据RS 码增量更新过程，校验块v'6可由式（4）计算得到，然后只需将增量块△v6发送到校验块中即可完成更新。

2 指标分析

从数据迁移量、I/O 开销两个影响扩容方法性能的关键指标方面对S-E-MBR、RR 与Scale-RS 3 种扩容方法进行比较，分析S-E-MBR 扩容方法的优缺点。比较时均假设在同一条带中进行。

2.1 数据迁移量分析

数据迁移量指完成一次扩容需要跨节点迁移的数据块数量。S-E-MBR、RR、Scale-RS 和Optimal 的数据迁移量如表1 所示，表中n'=n+s，d'=d+s，B'=k'd'-k'(k'-1)/2，分别表示扩容后的相应参数。

Table 1 The number of data blocks migrated by S-E-MBR，RR，Scale-RS，and Optimal in a same stripe表1 S-E-MBR、RR、Scale-RS和Optimal完成一次扩容迁移的数据块数量

在线扩容场景下，数据填充的最优情况为直接将得到的数据拆分为Vi(nd＜i＜=n'd')，然后将其填充至节点nodei(1 ≤i≤n') 对应位置，此时消耗的传输量为n'd'-nd。校验更新的最优情况为直接对2(θ-B)个校验块进行更新，此时消耗的传输量为2(θ-B)。可见在线扩容场景下，S-E-MBR 的数据迁移量与Optimal 一致，达到了理论最优传输量，这也是设计本文方法的目的。然而，RR 与Scale-RS 扩容方法未考虑在线场景与E-MBR 码的特点，迁移量较大，且RR 与Scale-RS 校验更新时只能采用重新编码得到冗余块后再进行更新，因此校验更新阶段的数据迁移量也较大。图4 为［n=4，k=2，d=3］、［n=5，k=2，d=4］、［n=5，k=3，d=4］参数下S-E-MBR、RR 和Scale-RS 方法分别扩容s=1 与s=2 个节点的数据迁移量示意图。当s=1 时，S-E-MBR 方法与RR、Scale-RS 相比迁移数据块数量减少了57%～74%；当s=2 时，S-E-MBR 方法与RR、Scale-RS 相比，迁移数据块数量减少了42%～50%。可见S-E-MBR 在数据块迁移量方面有明显优势。

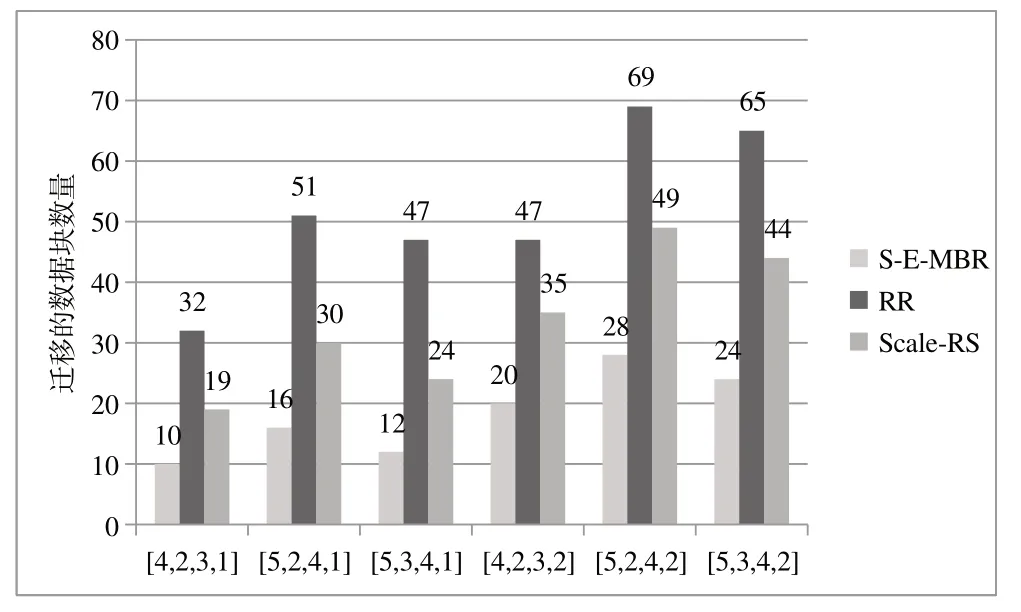
Fig.4 The number of data blocks that need to be migrated to expand the capacity of 1 and 2 nodes of S-E-MBR，RR，and Scale-RS scaling methods图4 S-E-MBR、RR和Scale-RS方法分别扩容1个和2个节点需要迁移的数据块数量

2.2 I/O开销分析

I/O 开销指完成一次扩容所有存储节点执行数据输入和输出的次数。S-E-MBR、RR、Scale-RS 的I/O 开销如表2所示。

Table 2 Input and output times of S-E-MBR，RR，and Scale-RS表2 S-E-MBR、RR和Scale-RS I/O 开销

I/O 开销与数据迁移息息相关，RR、Sclae-RS 方法的数据迁移次数较多，导致存储节点需要频繁读取，因而 I/O 次数较多。而S-E-MBR 方法利用聚合发送的方式，同一节点中只需要发送1 次数据，最大程度地减少了I/O 开销。图5 为S-E-MBR、RR 和Scale-RS 方法在参数为［n=4，k=2，d=3］、［n=5，k=2，d=4］、［n=5，k=3，d=4］时分别扩容s=1 与s=2 个节点的I/O 开 销。当s=1 时，S-E-MBR 方法与RR、Scale-RS 相比，I/O 次数减少了79%～89%；当s=2 时，S-E-MBR 方法与RR、Scale-RS 相比，迁移数据块数量减少了60%～79%。可见S-E-MBR 在I/O 开销上也有明显优势。

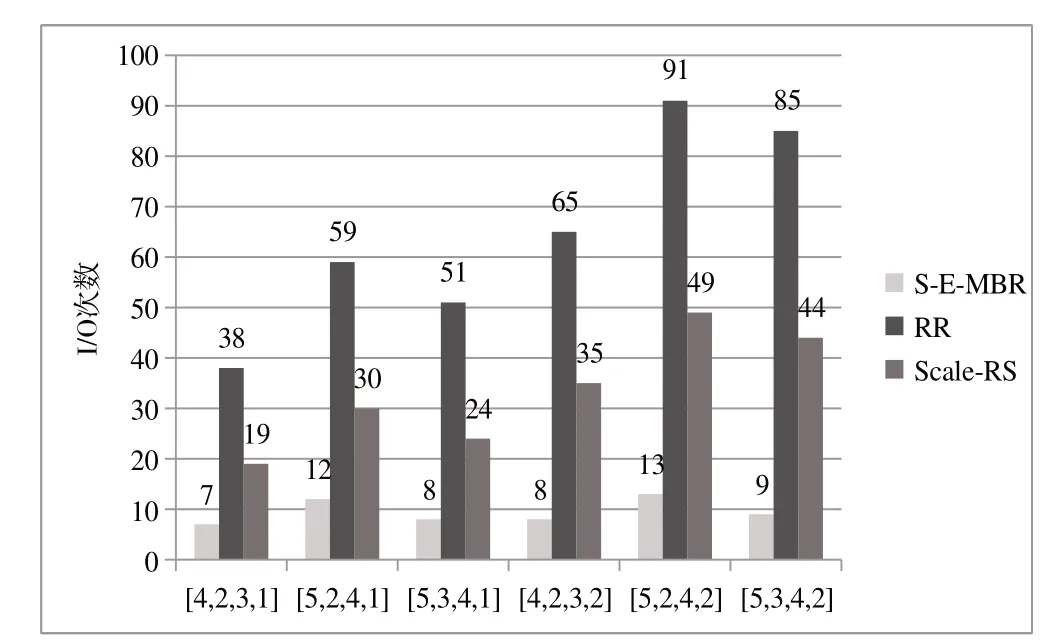
Fig.5 I/O overhead of S-E-MBR，RR and Scale-RS methods when scaling 1 and 2 nodes respectively图5 S-E-MBR、RR和Scale-RS方法分别扩容1个和2个节点时的I/O开销

3 实验评估

3.1 实验环境

在真实的分布式场景下测试S-E-MBR、RR、Scale-RS方法各方面的性能表现。实验平台基于Ceph 分布式存储系统搭建，主要分为客户端、Ceph Monitor、OSD（Object Storage Daemon）等。客户端主要用于提供用户操作集群的平台；Ceph Monitor 负责监控整个集群的健康状况、维护集群map 等；OSD 为对象存储设备，是存储用户数据并响应客户端操作请求的唯一组件。

实验测试平台包含23 个节点，分别为1 个客户端、2 个Ceph Monitor 节点和20 个OSD 存储节点。所有节点硬件配置相同，均为CPU 酷睿i5-5200U、8 GB 内存、128 GB 硬盘、1GBps 以太网卡，且均装载操作系统CentOS8、运行环境Python3.6、分布式存储系统Ceph15。

图6 为实验平台结构示意图。Ceph 中客户端可通过联系Monitor 获取集群map，并通过Ceph CRUSH 确定数据存储的OSD 位置，通过直接联系该OSD 来存取数据。所有实验操作均通过客户端调用扩容算法实现，并采用Ceph直接对OSD 中的数据进行读写操作。

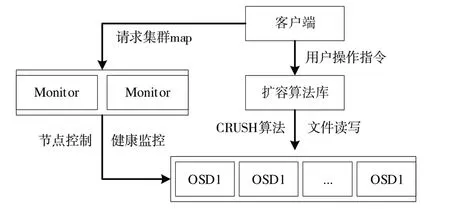
Fig.6 Schematic diagram of the experimental platform structure图6 实验平台结构示意图

3.2 实验设计与评价指标

为保证公平性，在每次实验开始前清除节点中的所有数据，然后以(n=10，k=8，d=9)E-MBR 码作为基础编码，以2M 的分块大小对50 G 数据进行编码，作为集群初始存储数据量。

选择数据传输量、扩容时间和客户端响应时间3 个指标对各方法性能进行评价与比较。在本文实验中，数据传输量被定义为整个扩容过程中涉及节点间传输的数据量之和，其直接反映了扩容过程中网络传输带宽的占用情况，也一定程度上反映了各个磁盘I/O 资源的占用情况，是评价扩容方法的重要指标；扩容时间被定义为从发出扩容指令开始到扩容结束所花费的总时间，其在一定程度上反映了算法实现的复杂度，也是衡量扩容方法效率的重要指标；客户端响应时间被定义为从客户端发出指令到服务器作出反馈的响应时间，其是扩容时用户最直观的感受。

3.3 数据传输量

图7 为在线输入数据为50 G 时，S-E-MBR、RR、Scale-RS 方法分别扩容2、4、6、8 个节点时的传输数据量比较结果，反映了扩容节点数s对扩容方法性能的影响大小。可以看出，在扩容节点数相同时，S-E-MBR 方法的数据传输量 比RR 和Scale-RS 方法分别减少52.7%～77.9% 和41.3%～50.4%。随着扩容节点数的增多，S-E-MBR 方法的数据传输量减少程度呈现下降趋势，说明该方法在小规模扩容时更具优势。

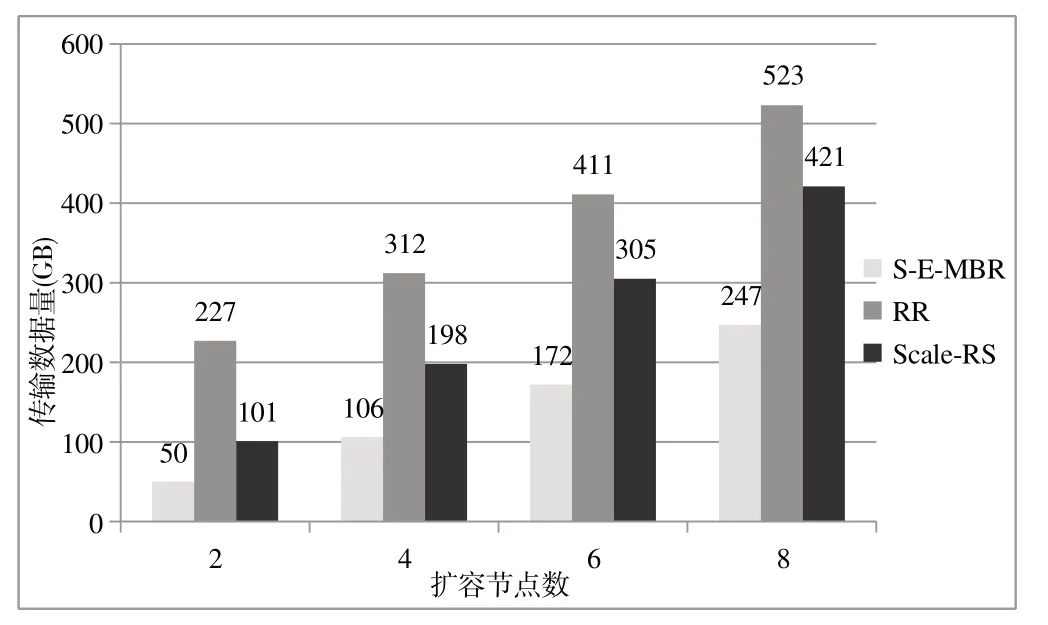
Fig.7 Data transmission volume comparison of S-E-MBR，RR and Scale-RS methods under different expansion nodes图7 不同扩容节点下S-E-MBR、RR和Scale-RS方法数据传输量比较

图8 为在线输入数据量分别为6 G、12 G、24 G、48 G，扩容1 个节点时S-E-MBR、RR、Scale-RS 方法的数据传输量比较。可以看出，在不同在线输入数据量下，S-E-MBR方法的数据传输量比RR 和Scale-RS 方法减少86.3%～86.8%，说明在线输入数据量大小对S-E-MBR 方法的数据传输量产生的影响较小，该方法稳定性较好。

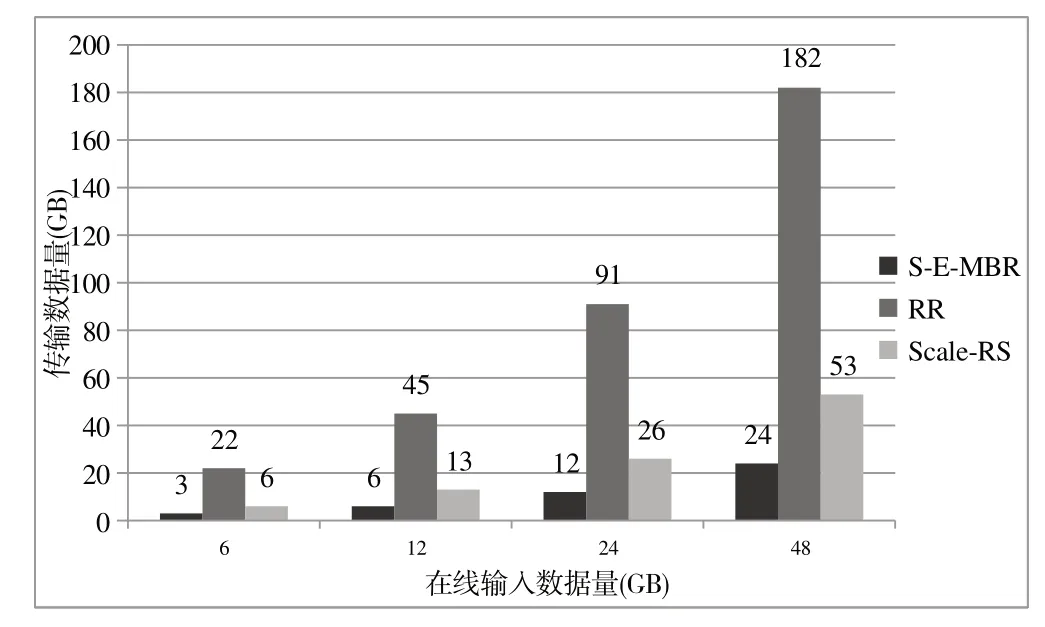
Fig.8 Data transmission volume comparison of S-E-MBR，RR，and Scale-RS methods under different online input data volumes图8 不同在线输入数据量下S-E-MBR、RR和Scale-RS方法数据传输量比较

3.4 扩容时间

图9 为在线输入数据量分别为6 G、12 G、24 G、48 G，扩容节点数为1 时，S-E-MBR、RR、Scale-RS 方法的扩容时间比较。可以看出，在不同在线输入数据量下，S-EMBR 方法的扩容时间相较RR 和Scale-RS 方法分别减少72.3%～75.4%和50.6%～53.5%，说明该方法在扩容时间方面有较小起伏。图10 为各方法扩容时间的平均值，可以看出S-E-MBR 方法的平均扩容时间相较RR 和Scale-RS方法分别减少了74.0%与58.2%，该方法在扩容时间方面具有明显优势。

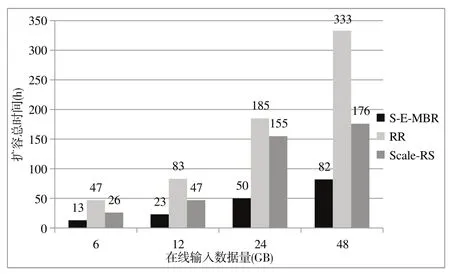
Fig.9 Expansion time comparison of S-E-MBR，RR，and Scale-RS methods under different online input data volumes图9 不同在线输入数据量下S-E-MBR、RR和Scale-RS方法扩容时间比较

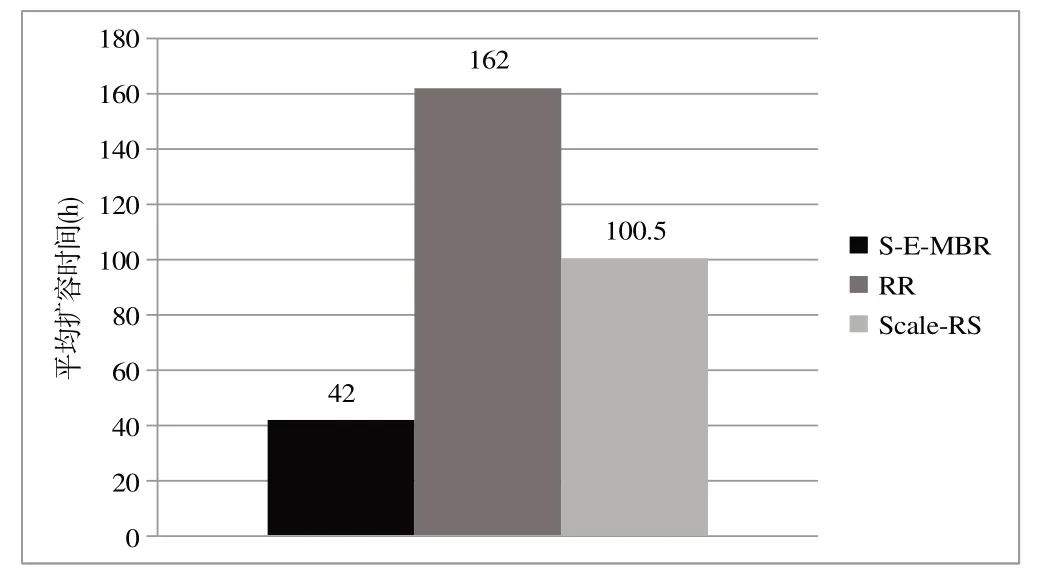
Fig.10 Comparison of average scaling time between S-E-MBR，RR，and Scale-RS methods图10 S-E-MBR、RR和Scale-RS方法平均扩容时间比较

3.5 客户端响应时间

图11 为S-E-MBR、RR、Scale-RS 方法以及无扩容操作的客户端平均响应时间比较，可以看出3 种扩容方法均在一定程度上降低了集群的响应速度，但执行S-E-MBR方法时集群的响应速度更快，与RR、Scale-RS 相比，其响应速度分别提升了39.2%和17.1%，说明S-E-MBR 方法更适合不宕机的在线扩容场景。

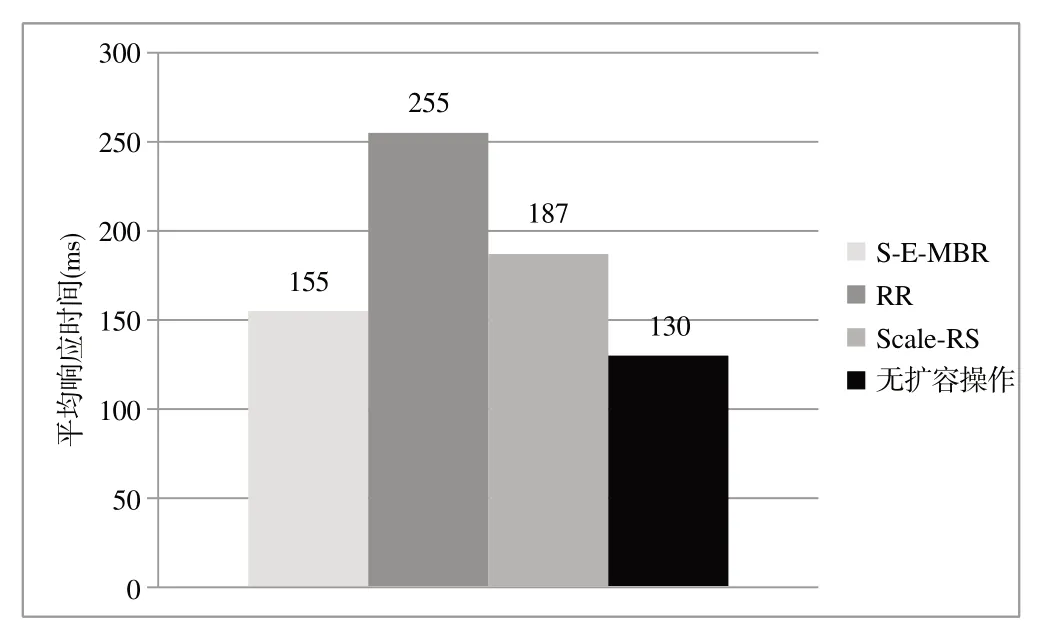
Fig.11 Comparison of client response time for S-E-MBR，RR，and Scale-RS methods图11 S-E-MBR、RR和Scale-RS方法客户端响应时间比较

4 结语

可以灵活扩充存储容量是分布式存储系统解决大数据难题的优势。在以E-MBR 码为基础构建安全策略的分布式存储中，扩容不仅是存储容量的增加，还意味着数据的重新分配与校验数据的更新。

本文充分利用E-MBR 底层RS 码的更新优势与在线扩容场景的特点，提出一种适用于E-MBR 码的分布式存储集群扩容方法S-E-MBR，其实现过程相较离线扩容更简单高效，在数据迁移与校验更新时均能达到最优情况，有效减少了需要消耗的网络带宽以及磁盘I/O 资源占用，缩短了扩容时间。在以Ceph 为基础搭建的分布式测试集群中进行比较实验，结果表明S-E-MBR 方法相较RR 与Scale-RS 方法扩容时的数据传输量减少了52.7%～77.9%和41.3%～50.4%，扩容总时间减少了72.3%～75.4% 和50.6%～53.5%。虽然S-E-MBR 扩容时会在一定程度上降低系统响应速度，但与RR 与Scale-RS 扩容方法相比，其响应速度分别提升了39.2%和17.1%，适合于需要在线扩容的场景。目前，S-E-MBR 方法仅适用于E-MBR 码需要增加节点的情况，节点数减少的情况将作为未来研究方向，以期提出更为通用、高效的在线扩容方法。