具有平带的一维十字型晶格中重返局域化现象*

陆展鹏 徐志浩2)†

1) (山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2) (山西大学极端光学协同创新中心,太原 030006)

1 引言

安德森局域化(Anderson localization)是凝聚态物理中重要概念,指的是在介质中引入无序会阻碍物质波的传播,即粒子波函数只分布在空间的一小段区域中,而无法向四周扩散,遍布整个系统.该现象于1958 年由Anderson 首次提出[1],并已在各类实验平台上得到了验证,包括冷原子[2,3]、微波腔[4,5]和光子晶体[6]等.安德森局域化对于理解无序系统中粒子的输运性质具有重要意义.根据单参数标度理论预测,在维度D≤2 的系统中,任意微弱的随机无序将导致系统的局域化[7].然而,在准周期系统中,该理论失效,即低维准晶体系可能出现金属-绝缘体转变.一维Aubry-André (AA)模型[8–11]作为一个范式已在冷原子[3]和光子晶体[12,13]等实验平台中实现,其特点是当准周期无序强度超过某一临界值时,所有本征态都会经历从扩展态到局域态的转变.这一临界值由其自对偶特性决定.而通过破坏AA 模型的自对偶性,可以实现扩展态和局域态共存的情况.两者由一临界能量分割开来,被称为迁移率边[14,15].此外,准周期系统还具有许多独特的性质,其中包括局域转变伴随拓扑相变[12],扩展态、局域态和临界态之间的多种局域化转变[16–21]以及一维Aubry-André-Fibonacci 模型中出现的瀑布型退局域化转变[21,22]等.

普遍认知中,无序系统发生局域化转变之后,系统的本征态会随着无序强度的增加一直处于局域态.然而,文献[23]研究表明,在一维二聚化模型中引入对角交错准周期势调制,系统会发生重返局域化现象.这意味着系统会随着无序强度的增强发生2 次局域化转变,即系统发生第1 次局域化转变后,如果继续增加无序强度并超过某个临界值,一些局域态重新变成退局域化态,而随着无序强度的进一步增加,系统再次进入完全局域相区.这2次局域化转变会经过2 个中间相区域,同时伴随着迁移率边的出现[24–31],并且系统中存在4 个转变点.最近非厄米系统中也发现了重返局域化及多次重返局域化的现象,并且重返局域化现象可以通过波包动力学进行探测[32–36].

一维平带晶格是一种具有平移不变性的紧束缚晶格,其能谱含有不依赖于动量的能带[37],因此电子的动能就被完全冻结了,弱相互作用能在量子相变中起主导作用.通常平带系统被认为是一个理想的探索强关联物理的平台[38].最近,在一维平带系统研究中呈现了一些奇特的局域化性质,引起了人们的关注.比如非传统局域化长度的标度行为[37],局域态与临界态之间的转变[39,40],存在解析的迁移率边[41–43]等.平带上电子的实空间波函数是严格局域化的,被称为紧凑局域态[37].而平带系统可以通过紧凑局域态所占据的原胞的个数U来区分.而一维十字型晶格就是U=1 的经典平带模型,即紧凑局域态只占据在一个原胞中.作为平带模型的范式,人们已经在其基础上做了大量的研究.如平带态寿命[44]、螺旋量子输运[45]等.本文研究了具有准周期调制的一维十字型平带晶格.发现经过局域规范变换,系统清晰地展现了双频调制的特点,进一步通过数值计算证实了重返局域化的存在.当系统恢复成单频率调制时,通过解析和数值手段证明了,系统存在解析的迁移率边,但不存在重返局域化.这一结果为平带系统中研究重返局域化现象提供了参考.

2 理论模型

如图1 所示,本文考虑一个由L个原胞(2L格点)构成的一维十字型晶格,其中绿色虚线表示由A 和B 两种子格组成的一个原胞,黑色虚线代表胞内跃迁,黑色实线代表胞间跃迁.在紧束缚近似下,系统的哈密顿量可以表示为

图1 一维十字型晶格示意图.绿色虚线代表一个原胞.t 代表胞内跃迁强度,J 代表胞间跃迁强度Fig.1.Schematic diagram of the cross-stitch lattice.Each unit cell with two sublattices (A and B) is shown in the green dotted box.t and J are the intracell and intercell hopping amplitudes.

其中Hf和Hε分别为跃迁部分和在位势部分.Hf的具体形式为

这里t代表胞内跃迁强度;J代表胞间跃迁强度(J被设定为能量量纲代表在第n个原胞的 A(B) 子格上粒子的产生算符;cn,A(cn,B)代表在第n个原胞的 A(B) 子格上粒子的湮灭算符.Hε为在位势部分,其具体形式为

这里εn和 -εn是分别加在第n个原胞A 和B 子格上的在位势,εn=∆+2λcos(2πβn) ,其中∆为一个常数势,λ 为准周期势强度,β 是一个无理数.

此时系统的本征方程可以写成

将(4)式写到旋转后的基矢下,等式变为

如果εn=0 ,则(7)式中第2 个等式化简成:Efn=tfn,则关于fn的本征方程中本征能量为常数t,即平带.且fn只有在第n个原胞上才有取值,在其他原胞上全部为0,这也就证实了fn对应的本征态,即紧凑局域态.如果εn≠0,将(7)式中2 个等式结合并消除fn可得

(8)式中 4∆λcos(2πβn) 和 4λ2cos2(2πβn) 提供了两种不同频率的准周期调制.最近有文章猜测多频率调制可诱导重返局域化现象的出现[24,29,46].为了验证这一猜测,本文通过数值方法来讨论此模式的局域化特性.注意当∆≠0 时,将恢复成单频率调制,此时系统存在解析的迁移率边[42],此时系统中不存在重返局域化.

为了研究系统的局域化性质,引入逆参与率(inverse participation ratio,IPR)、归一化参与率(normalized participation ratio,NPR)、分形维度(fractal dimension)等序参量,相关定义如下.

对于第i个本征态,逆参与率(IPR)和归一化参与率(NPR)的定义分别为[23,47–50]

当L→∞时,如果本征态是局域态,则 IPRi为有限值,NPRi趋于0;如果本征态是扩展态,则 IPRi趋于0,NPRi为有限值.进一步地,可以定义平均逆参与率( MIPR)和平均归一化参与率( MNPR)分别为[23]

MIPR 和 MNPR 可以描述整个系统所有本征态的局域化转变.当系统处于完全扩展相时,MIPR的值趋于0,MNPR 为有限值;当系统处于完全局域相时,MIPR 为有限值,MNPR 的值趋于0;而如果系统处于中间相,即系统存在迁移率边,此时 MIPR 和 MNPR 都为有限值.利用 MIPR 和MNPR可以定义η=lg(MIPR×MNPR),η 可以把具有迁移率边的中间相从完全扩展和局域相中清晰区分出来,即L→∞时,如果系统处于中间相,η 的值大于 -lg(2L) ;而系统处于完全扩展或局域相时,η 的值小于 -lg(2L)[23].

为了更精确表征系统的局域化转变,可以计算每个本征态的分形维度.对于第i个本征态,分形维度Γi的定义为[50]

在热力学极限条件下,Γi→1 对应本征态为扩展态;Γi→0 对应本征态为局域态.

本文计算中考虑t=1,β=(黄金分割比),选定合适尺寸,写出格点表象下哈密顿量(1)式对应的矩阵形式,通过精确对角化法,数值计算出上述序参量从而分析出系统的局域化特性.

3 结果分析与讨论

3.1 双频率调制

对于重返局域化现象的研究受到越来越多的关注,但其出现的机理仍然存在争议.最近,有研究者在研究单带和光腔系统的过程中发现,多频率调制可能是出现重返局域化现象的关键因素[24,29,46].从(8)式可知,对具有平带的一维十字型准周期调制的晶格,进行局域转动后,系统中清晰地展现出两种不同的准周期调制频率,这两种不同的调制提供了两种不同的周期标度.那么此系统是否也存在着由双频率调制导致的重返局域化现象呢? 为了证明系统中重返局域化现象的存在,下面展示了不同序参量的数值计算结果.

以∆≠1.68 作为一个具体例子,图2(a)展示了 MIPR 和 MNPR 随着无序强度λ 的变化情况.在图2(a)中,随着λ 的增加,存在两个 MIPR 和MNPR对应值都不为0 的区间(阴影部分).当λ<0.27时,MIPR 值为0,而 MNPR 为有限值,表明此时系统处于完全扩展相.当 0.27<λ<2.01 时,MIPR 和MNPR都保持有限值,表明系统处于中间相.当2.01<λ<2.48 时,MIPR 为有限值,而 MNPR 的值为0,表明系统进入到完全局域相.不同于通常情况,继续增加无序强度,系统会一直处于局域相,局域化程度会越来越高.在 2.48<λ<2.83 区间,MIPR 和 MNPR 又重新 恢复成 都为有限值的情况,表明此时系统又再次进入中间相.当λ>2.83 ,MIPR为有限值,而 MNPR 的值为零,系统再次进入完全局域相.为了研究尺寸效应,图2(a)插图展示了不同尺寸下,MNPR 随着无序强度λ 的变化.可以看到,不同尺寸下,当 2.48<λ<2.83 时,MNPR 确实变为了有限值,说明系统确实进入到了存在迁移率边的中间相内.并且从插图可以看到,在第2 个中间相,即出现重返现象的区间中,随着无序强度λ 增加,MNPR 值的变化不是规律的,在λ=2.6和2.72 处出现2 个峰值,表明此时系统中产生了较多的非局域态.图2(a)中以∆≠1.68 作为一个具体例子,研究了系统的局域化特性.发现随着无序强度λ 的增加,系统发生2 次局域化转变,存在4 个局域化转变点.这一转变过程展示了典型的重返局域化现象[23].

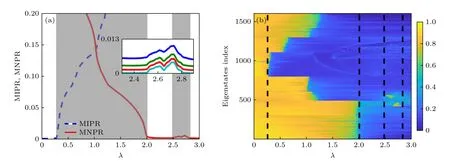
图2 当 ∆≠1.68 ,L=800 时,(a) MIPR (蓝色虚线)和 MNPR (红色实线)随着无序强度λ 的变化,灰色区域表示具有迁移率边的中间相区;插图显示当 L=300 (蓝色实线),500 (深绿色实线),800 (红色实线)和1500 (湖蓝色实线)时,MNPR 随无序强度λ 的变化.(b)分形维度 Γi 随着本征态指标(eigenstates index)和无序强度λ 的变化.系统存在4 个局域化转变点:λ=0.27,2.01,2.48 和2.83 (黑色虚线表示).图中的颜色条代表分形维度 Γi 的大小Fig.2.(a) MIPR (blue dashed line) and MNPR (red solid line) as a function of the disorder strength λ.The shaded regions represent the intermediate regimes with the mobility edges.The inset shows the MNPR as a function of the disorder strength λ for L=300,500,800,and 1500,which are marked by blue,bottle green,red and lake blue lines,respectively.(b) The fractal dimensionΓi associated with the eigenstate indices as a function of λ.The colorbar indicates the magnitude of Γi .There exist four localization transition points λ=0.27,2.01,2.48,and 2.83,which marked by the black lines.Other parameters: ∆≠1.68 and L=800 .

图2(b)绘制了∆≠1.68 时,分形维度Γi随着本征态指标和无序强度λ 的变化曲线,其中,4 条黑色虚线从左到右分别对应着图2(a)中的4 个局域化转变点.从图2(b)可以直观地看出,λ<0.27时,所有态的Γi值都趋于1,系统处于完全扩展相.0.27<λ<2.01 和 2.48<λ<2.83 时,部分态的Γi值趋于 0,部分态的Γi值趋于1,系统处于2 种态并存的中间相区.在 2.01<λ<2.48 和λ>2.83 的区间内,所有态的Γi都趋于0,系统处于完全局域相.可以看出,随着无序强度λ 的增加,系统经历了2 次局域化的过程,系统存在4 个局域化转变点,分别为λ=0.27,2.01,2.48 和2.83.并且发现,第二个中间相( 2.48<λ<2.83 )内,在λ=2.6 和2.72 附近,第470—550 个能级之间出现了2 个Γi值趋于1 的小型黄色区域,说明系统中有较多的非局域态.这与图2(a)插图中的2 个峰值对应.图2(b)研究了分形维度Γi值随着无序强度λ 的变化,发现系统确实发生2 次局域化转变,且存在2 个中间相区.这与图2(a)中的结果对应.该过程更加清晰地描述了重返局域化现象的出现.

为了进一步验证重返局域化现象是否真实存在,分别在扩展区、局域区和中间相区,研究MNPR的标度变化.图3(a)给出了λ=0.1 ,∆≠1.68 时,MNPR 随尺寸L变化的情况,可以看出当L→∞时,MNPR 趋近为一个有限值,约为0.48.当λ=2.32,∆≠1.68 时,如图3(b)所示,MNPR→0,表明此时系统中所有的本征态都为局域态.当λ处于中间相区时,以λ=2.72 ,∆≠1.68 为例,如图3(c)所 示,L→∞时,MNPR 随 着L增 加线 性衰减,并趋近于一个有限值,约为 0.004,远小于扩展相区的值,表明此时系统中既存在扩展态又存在局域态,即存在迁移率边.图3(a)—(c)分别在扩展相、局域相和中间相中选取λ=0.1,2.32 和2.72三个参数点,研究其对应的 MNPR 的标度行为.发现它们具有不同的局域特点.该结果与图2(a)的结果相符合,通过有限尺寸分析说明重返局域化在系统中稳定存在.

图3 (a) λ=0.1 ,(b) λ=2.32 ,(c) λ=2.72 时,MNPR 随 1/L 变化.这里,∆≠1.68Fig.3. MNPR as a function of 1/L for (a) λ=0.1 ,(b) λ=2.32 and (c) λ=2.72 ,respectively.Here,∆≠1.68 .

参数η 可以把中间相从扩展和局域相中清晰地区分出来.图4 给出了∆-λ参数平面内,以η 的大小为填充颜色的局域化相图.其中,绿色区域代表了完全局域相或完全扩展相,红蓝色区域代表了具有迁移率边的中间相.可以看到当∆大约处于(1.6,1.9)参数范围时,随着无序强度λ 的增大,系统经历第1 次局域转变到达完全局域相后,又重新回到中间相,最终经历第2 次局域转变到达完全局域相,此时体系中存在重返局域化现象.

图4 ∆-λ 参数平面内的局域化相图,其中绿色区域表示完全扩展或局域相,红蓝色区域表示具有迁移率边的中间相.颜色条代表序参量η 的大小.这里L=800Fig.4.Localization Phase diagram in the ∆-λ plane,where the green regions denote the full extended or localized phase and the red and blue regions represent the intermediate phase the mobility edges.The colorbar represents values of η.Here,L=800 .

3.2 单频率调制

上述结果分析了当参数∆≠0 时,双频率调制下,系统中的重返局域化现象.当参数∆≠0 时,(8)式可以化简为下面的形式:

从(12)式可知,系统中只存在 4λ2cos2(2πβn) 这一种准周期调制,系统回归到单频率调制情况.其中

结合(12)式和(13)式,化简可得

从(15)式的结果可以看出,此时系统的局域化转变点和能量有依赖关系.(15)式即为迁移率边的表达式.

图5 给出了不同能量本征态的分形维度Γi随着无序强度λ 的变化情况.从图5 可以看出,解析结果和数值结果相符合,2 条红色实线以内本征态对应的分形维度Γi值趋于0,对应于局域态.而2 条红色实线以外的本征态对应的分形维度Γi值趋于1,对应于扩展态.可以发现,当系统恢复到单频率调制的情况,系统中存在解析的迁移率边,但不存在重返局域化现象.从上述结果中发现,如果系统只存在一种准周期频率,则保留了能量依赖的自对偶性,导致系统存在解析的迁移率边,且只存在一次局域化转变,类似于参考文献[14,15,42].但是如果系统中存在2 种准周期频率,则破坏了这种与能量依赖的自对偶性,而且这2 种准周期频率提供了2 种不同的能量标度,这2 种不同的能量标度存在竞争,正是这2 种不同的能量标度的竞争导致了系统中重返局域化现象的发生.

图5 分形维度 Γi 随着调制强度λ 和本征能量E 的变化.其中红色实线代表迁移率边的表达式(15).图中的颜色条代表 分形维度 Γi 的大小.其他参数为: L=800 ,t=1Fig.5.The Γi of the eigenstates as a function of he disorder strength λ and the eigen energy E.The red solid line represents the analytical expression (15) of the mobility edge. The colorbar represents the values of Γi . Here,L=800 and t=1 .

4 总结

本文研究了具有平带的一维十字型准周期调制的晶格.发现当参数∆≠0 时,系统存在两种不同的准周期调制频率,然后通过数值分析,证明了重返局域化现象 的存在,并且得到 了∆-λ参 数空间的局域化相图.而当参数∆≠0 时,系统只存在一种准周期调制频率,通过解析和数值手段证明了,系统存在解析迁移率边,但不存在重返局域化现象.该工作为平带系统中研究重返局域化现象提供了参考,也为重返局域化的研究提供了新的角度.