面向异构效用的移动群智感知多目标任务分配

傅彦铭 陆盛林 祁康恒 许励强 陈嘉元

摘 要：当前移动群智感知（MCS）任务分配往往只考虑工人或平台单方面的效用，并且效用的构成也不够全面。因此基于工人信誉指数和任务熟练指数，设计了工人和平台两方面的异构效用机制，并提出一种双种群竞争的多目标进化算法（DCMEA）来获得最优的工人和平台异构效用。该算法首先通过随机贪婪初始化种群，然后使用二元竞标赛算法将种群划分为胜者种群和败者种群，并针对每个种群采用不同的进化策略。最后，通过修复算子使进化过程中的无效个体满足约束条件。在真实场景的数据集上进行实验表明，与基线算法相比，DCMEA收敛速度更快，能够找到精度更优、稳定性更好的任务分配解集，同时在更为复杂的场景中依然能够保持其性能。

关键词：移动群智感知；多任务分配；多目标优化；双种群竞争进化；信誉指数；任务熟练指数

中图分类号：TP393.01   文献标志码：A   文章编号：1001-3695（2024）01-023-0159-06

doi：10.19734/j.issn.1001-3695.2023.04.0186

Multi-objective task assignment towards heterogeneous utilities in mobile crowdsensing

Abstract：Most of the existing MCS task allocation methods often only consider the unilateral utility of workers or platforms，and the composition of utility is not comprehensive enough.Therefore，this paper designed a heterogeneous utility mechanism for both workers and platforms based on the worker reputation index and task proficiency index.It proposed a dual-population competitive multi-objective evolutionary algorithm （DCMEA） to obtain the optimal worker and platform heterogeneous utilities.The algorithm firstly initialized the population using a stochastic greedy algorithm，then divided the population into a winner population and a loser population using a binary bidding tournament algorithm，and employed different evolutionary strategies for each population.Finally，this paper proposed the repair operator to make the invalid individuals in the evolution process satisfy the constraint.Experiments on real-world datasets show that DCMEA converges faster than the baseline algorithm，and can find more accurate and stable task allocation solution sets，while maintaining its performance in more complex scenarios.

Key words：mobile crowdsensing；multi-task allocation；multi-objective optimization；competitive evolution of two populations；reputation index；task proficiency index

0 引言

移動群智感知（MCS）来源于“众包”，通过参与者持有移动设备相互合作完成众多的任务，是一种新的感知范式［1，2］。移动互联网、5G等技术的发展使任何具有微型传感器的移动设备（如智能手机和平板电脑）携带者都可以成为MCS中的数据源。由于在收集感知数据方面具有高效性和扩展性，MCS在不同的领域中具有广泛应用，例如：环境监测［3］、交通规划［4］、公共安全［5］、医疗保健［6］。MCS包含任务发布、任务分配、任务执行和数据收集四个阶段。其中，任务分配是MCS的核心问题［7］。

从给每个工人分配的任务数角度，MCS任务分配可以分为单任务分配和多任务分配。单任务分配是每次只给可用工人分配单项任务。文献［8］提出了一种冲突感知参与者招募机制，能够有效提高平台效用，同时保证在完成感知任务时无冲突。文献［9］提出一种强大的隐私保护MCS方案，支持基于地理信息和移动用户信用点的精确任务分配。然而，随着MCS任务数量的增加，任务之间相互关联，在有限的资源下，单任务分配会使工人完成任务的效率变低，MCS平台无法获得较好的整体效用。因此，多任务分配给一个工人同时分配多个任务来优化平台的整体效用。文献［10，11］采用多任务分配方案，在任务共享有限的激励预算时，使系统的整体效用最大化。文献［12］提出了一个具有时间约束和平台效用最大化的多任务分配问题，并设计了两种遗传算法来求解该问题。文献［13］提出了一种以最大化平均感知质量为目标的综合空间覆盖和感知精度的多任务分配方法，并引入改进的遗传算法求解。

上述任务分配只考虑优化一个目标［14，15］，属于单目标优化问题，而在分配过程中往往需要同时考虑优化多个目标，以获得符合多方利益的任务分配方案。文献［16］设计了一种基于粒子群优化的多目标任务分配算法，最大化感知质量和预算的比值，同时最小化响应时间。文献［17］对单任务分配提出了一种改进的进化算法，通过平衡因子来选择用户，最大化参与者的总回报和感知质量。文献［18］同时考虑了最大化感知质量和最小化激励支付，通过帕累托最优粒子群算法解决多目标多任务分配。文献［19］建立了一种基于变速多任务分配的多目标优化模型，并提出了一种三阶段多目标洗牌蛙跳算法解决该模型。然而，在这些多目标分配模型中只考虑了工人的异质性，例如工人的执行意愿、信誉度、旅行速度等因素，而忽略了任务的异质性。在实际分配中，不同类型的任务需要的感知数据并不相同，因此平台需要匹配合适的工人以提高效用。

本文综合考虑了工人和任务的异质性，引入工人信誉指数和任务熟练指数，提出了一种优化工人和平台两方面异构效用的MCS多任务双目标优化任务分配方案。结合问题的特点，设计了一种双种群竞争的多目标进化算法（DCMEA）来求解该问题。此外，在真实场景数据集上验证了DCMEA求解本文的MCS任务分配方案能够获得优于对比算法的精度和稳定性。

1 异构效用MCS多目标任务分配模型

1.1 模型描述

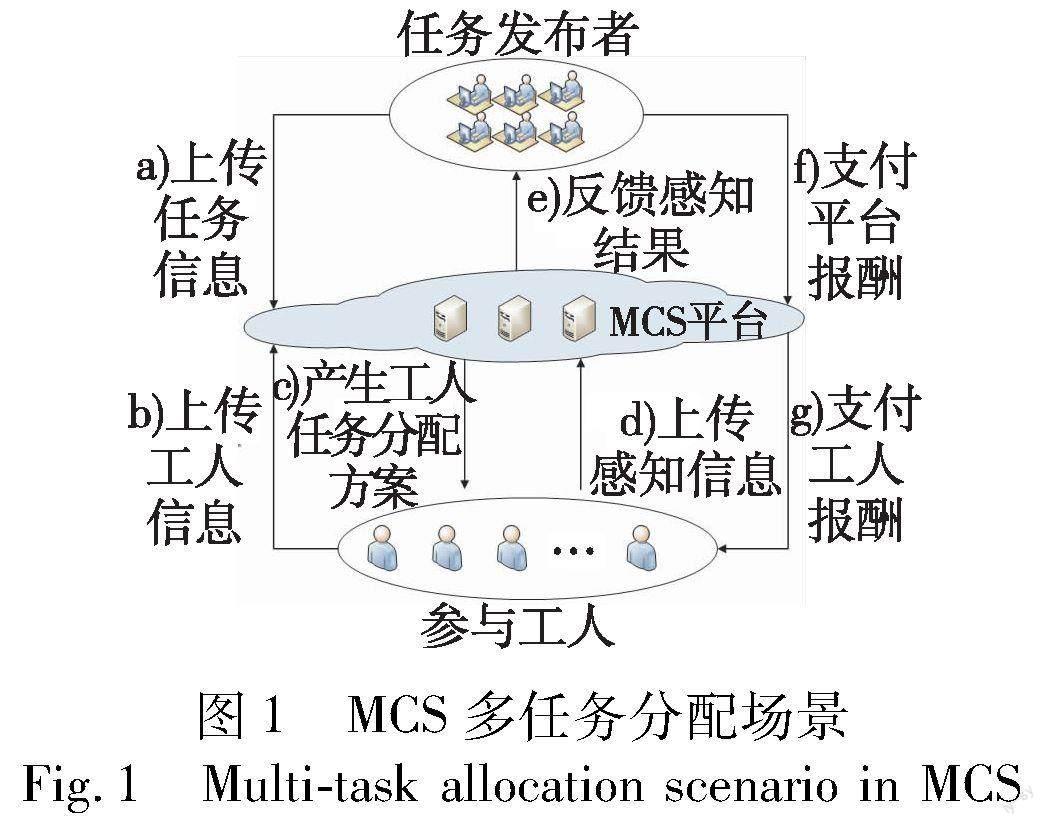
MCS包括一个中心平台、多个任务发布者及参与工人，其工作流程可用图1描述。首先，发布者将任务需求上传到平台，平台在获得任务信息后使用相关的任务分配算法将任务分配给工人。接着，工人完成任务后，将任务完成的结果或感知数据上传到平台。最后，平台收到感知数据后将结果反馈给任务发布者，并获得相应报酬，同时给工人支付报酬。

若在MCS任务分配中有m名工人参与，W={w1，…，wi，…，wm}。工人wi包含以下信息：wi={lati， lngi，wnummaxi，Ri}。其中lati，lngi表示工人的经纬度坐标；wnummaxi表示工人的最大完成任务数，工人不能重复完成相同的任务；Ri为工人的信誉值，表示工人历史完成任务的质量和性价比［20］。其中Ls≤Ri≤Lm，Lm为最大信誉值，Ls为最小信誉值。

任务发布者发布了n个任务T={t1，…，tj，…，tn}，任务tj包含以下信息：tj={latj，lngj，tnummaxj，bj，wrj，Skj}。其中：latj和lngj表示任务的经纬度坐标；tnummaxj表示任务最多可以由多少名不同工人完成；bj为工人每次完成任务tj平台所获得的报酬。wrj为完成任务tj工人获得的固定报酬。Skj={sk1j，…，skij，…，skmj}，skij表示工人wi对任务tj的熟练度，其中-1≤skij≤1，skij值越大说明工人对任务越熟悉。

wtij表示一个任务分配，若平台将任务tj分配给了工人wi，则wtij=1，否则wtij=0。当wtij=1时，工人在完成任务后，分别产生相应的工人异构效用uwij和平台异构效用upij。当wtij=0时，uwij和upij的值为0。

1.2 异构效用机制

为了充分考虑MCS中工人和任务的异质性，从工人信誉和工人对任务的熟练程度两个角度出发，定义了工人信誉指数和任务熟练指数两个指标。

1）工人信誉指数 工人wi的信誉指数Hi用来描述工人信誉的良好程度。指数越高，其完成任务的质量越高，反之亦然。Hi可用式（1）计算［20］。

2）任务熟练指数

任务熟练指数Tij用来描述工人wi对任务tj的熟悉程度。任务熟练指数越高，工人对任务越熟悉，完成任务的质量越高且感知的数据也越准确。Tij可以用Gompertz函数来计算，如式（2）。Gompertz函数描述了事物的发生、发展和成熟三个阶段，并已应用于任务分配建模中［21］。

本文设计了异构效用机制。工人在完成一个任务后会有一个固定的奖励报酬RF，并通过信誉指数和任务熟练指数产生一个奖励指数ηij，獎励报酬和奖励指数相乘得到工人完成任务后获得的激励报酬。将激励报酬加入到工人效用和平台效用中，更全面地反映了不同任务分配间的效用差异。

3）工人异构效用

工人wi完成任务tj所产生的工人异构效用由式（3）计算。由固定报酬wrj、激励报酬ηij×RF和花费crij三部分组成。

uwij=wrj+ηij×RF-crij（3）

其中：ηij为奖励指数，由信誉指数Hi和任务熟练指数Tij计算，如式（4）所示。

crij=p×dsij为工人到任务地点的旅行消耗，其中p为每米花费系数，dsij由Haversine formula计算得出：

4）平台异构效用

工人wi完成任务tj产生的平台异构效用upij由式（6）计算。由平台报酬bj、固定报酬wrj和激励报酬ηij×RF组成。

upij=bj-wrj-ηij×RF（6）

1.3 基于异构效用的多目标任务分配模型

基于异构效用的多目标任务分配即要寻找最优任务分配方案，使得完成任务能够获得最大化的工人效用和平台效用。该问题可以表示为如下的约束双目标优化模型。

其中：式（7）（8）分别表示最大化工人和平台获得的异构效用；式（9）～（11）为任务分配的约束，分别表示每个工人wi完成的任务数不能超过wnummaxi、任务tj分配给不同工人的数量不能超过tnummaxj，wtij的取值为0或1表示同一个任务最多只能分配给同一工人一次。

2 异构效用MCS多目标任务分配模型求解

MCS多任务分配的解集空间较大，是一个NP-hard问题，无法在多项式时间内求解，因此考虑使用启发式算法来解决。进化算法已应用于MCS任务分配领域［12，13，17］，其特性也适合于本文的多任务分配问题。本文根据问题的特点设计了双种群竞争的多目标进化算法（DCMEA）来求解模型，如算法1所示。

算法1根据工人集W和任务集T的信息，对个体进行序列编码，并采用随机加权贪婪策略生成初始化种群SP。接着，通过二元锦标赛算法将SP划分为勝者种群WP和败者种群LP。对这两个种群执行不同的交叉和变异操作，使WP注重局部搜索、LP注重全局搜索，实现竞争进化。之后，设计了修复算子对不满足约束的无效解修复，以保留无效解中的有用信息。最后，将SP、WP和LP种群合并，根据任务分配解的UW和UP值，采用精英保留策略生成下一代种群SP。循环执行上述双种群进化过程，直至最大迭代次数，得到最优的MCS任务分配方案集。

算法1 DCMEA

输入：工人集W；任务集T；种群大小N；最大迭代次数times。

输出：迭代后任务分配解集。

根据算法2初始化任务分配解集种群SP

for i=1：times do

根据算法3将种群SP划分为胜者种群WP和败者种群LP，并更新WP和LP使其朝着不同方向进化

根据算法4修复WP和LP中更新后产生的无效解

合并SP、WP、LP生成新的种群NewP

采用精英保留策略在NewP中选取前N个解生成子代种群NP

SP=NP

i=i+1

end for

return SP

2.1 个体编码方式

通常MCS任务分配会采用0-1编码的方式，用大小为m×n的数组表示种群个体［13］。行标为工人，列标为任务。数组元素为1表示分配给工人对应的任务，否则为0。随着任务和用户数量的增加，0-1编码会使矩阵包含大量元素“0”，变得稀疏。本文采用基于工人路径的序列编码，用一维数组表示一个可行的任务分配方案（种群个体Ci），如图2所示。Ci由m个片段组成，每个片段的大小不超过工人可完成的最大任务数wnummaxi。每个片段中的数字表示任务的编号，工人根据编号按序完成任务，若没有分配任务则用0表示。

2.2 随机加权贪婪初始化

用随机化的方式初始化种群容易生成无效解，也缺乏较优的解来引导种群朝优化的方向搜索。在多目标问题的求解中，线性加权法是一种常用的方法。对多个目标函数加权重，将多目标问题转换为单目标问题，本文的两个优化目标可以转换为

U=ε×UP+（1-ε）×UW（12）

算法2 随机加权贪婪初始化

输入：任务集合T，工人集合W。

输出：初始种群SP

while i≤N do

生成没有任务序号的个体Ci

创建候选工人集CWW

创建候选任务集CTT

随机生成加权权重ε

repeat

从CW中随机选择一名工人wr

while j≤wnummaxr do

从CT中贪婪地选择U值最大的任务ts

将任务ts的序号添加到Ci中wr的片段中

tnummaxs=tnummaxs-1

if tnummaxs≤0 do

CTCT-{ts}

end if

j=j+1

end while

CWCW-{wr}

until CW= or CT=

SP=SPU{Ci}

end while

return SP

上述初始化算法具有以下优势：a）基于实际问题约束的初始化方法可以避免生成无效初始解；b）基于贪婪策略的线性加权法获得的解作为种群的初始化解可以引导种群朝优化方向进化；c）通过随机生成加权权重ε和工人的任务分配顺序，可以保证初始种群的多样性。

2.3 双种群竞争进化

用二元锦标赛算法将种群划分为胜者种群和败者种群，并对两个种群采用不同的更新策略，使两个种群沿着不同方向进化。因此在进化过程中能够增加种群的多样性和随机性，使得算法能够跳出局部最优，提升算法的收敛精度和速度。

1）二元锦标赛划分种群

首先对种群的个体进行非支配排序、计算拥挤度距离。之后随机选择两个个体，根据Pareto排序等级进行比较，等级高的为胜者，低的为败者。若Pareto等级相同，进行拥挤度距离比较，拥挤度距离大的为胜者，小的为败者。在进行N次比较后，将前N/2次比较的胜者构成WP种群，后N/2次比较的败者构成LP种群。

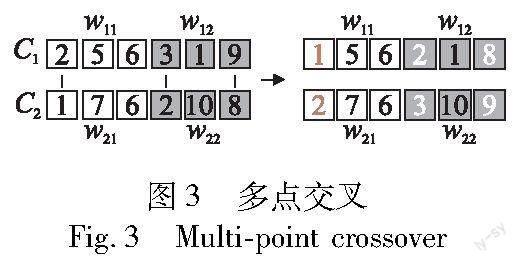
2）胜者种群进化策略 WP种群在进化时注重局部搜索。首先采用多点交叉策略，选择种群中C1和C2两个个体，生成3～5个交叉点，交换C1和C2交叉点上的元素。如图3所示，假设C1和C2有两个工人，每个工人有三个任务，在个体C1和C2上生成三个交叉点，由竖线表示。将交叉点上的任务（2，1），（3，2），（9，8）交换后生成新的个体。

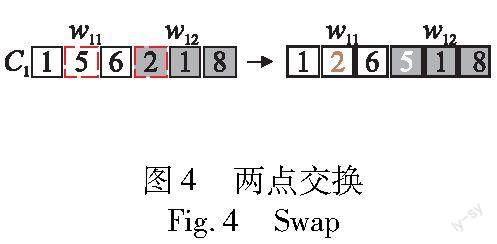
多点交叉后对新产生的个体采用两点交换操作，在新个体上随机生成两个变异点，交换两点上的任务生成新的个体。如图4所示，将个体C1中虚线方框的任务（5，2）交换后生成新的个体。

胜者种群利用小范围内的交叉变异操作，保留原有个体的优秀属性，侧重于在局部范围内搜索更优解。

3）败者种群进化策略

LP种群进化时注重全局搜索。选择种群中个体C1和C2，采用顺序交叉策略生成两个新个体。如图5所示，在个体C1和C2上生成两个交叉点，由虚线表示。两条虚线间的任务，即C1中的任务（5，6，3），C2中的任务（7，6，2）固定不变。在C1中去掉在C2固定部分（7，6，2）中出现的任务得到替换序列（5，3，1，9）。用该序列顺序替换C2可变部分（1，10，8），更新C2得到（5，7，6，2，3，1）。在C2中去掉在C1固定部分（5，6，3）中出现的任务得到替换序列（1，7，2，10，8）。用该序列顺序替换C1可变部分（2，1，9），更新C1得到（1，5，6，3，7，2）。

顺序交叉后对新生成的个体采用Scramble变异的策略，在新个体上随机生成3～5个变异点，将元素按新的顺序随机重新排列生成新的个體。如图6所示，将个体C1中虚线方框内的任务（5，3，7）随机排序生成（3，7，5），交换任务后生成新的个体。

顺序交叉和Scramble变异增大了个体中元素的改变幅度，扩大了种群的搜索空间，有利于生成新的优秀个体。

双种群竞争进化如算法3所示。由于选择的概率导致双种群中存在少量的相同解。在进化过程中，优势解局部搜索，劣势解全局搜索，相同解则同时朝着两个方向进化。种群沿着多个方向进化，增强了种群的多样性和随机性，能够提高算法的寻优能力。

算法3 双种群竞争进化

输入：种群SP。

输出：进化后新种群WP、LP。

对SP采用二元锦标赛算法生成胜者种群WP和败者种群LP

for i=1：（N/4」） do

在WP中选择个体Cwi，Cw（i+N/4」）

采用多点交叉生成两个新个体替换原有个体

在LP中选择个体Cli，Cl（i+N/4」）

采用顺序交叉生成两个新个体替换原有个体

i=i+1

end for

for j=1：（N/2） do

对WP中个体Cwj采用两点交换生成新个体替换原有个体

对LP中个体Clj采用Scramble变异生成新个体替换原有个体

j=j+1

end for

return WP，LP

2.4 修复算子

由于实际问题约束的特殊性，在进化过程中可能会产生无效的任务分配解。本文结合任务分配模型设计了修复算子，将无效解修复成有效解，并保留其中有用的信息。图7展示了个体C1的修复过程。假设个体C1有三个工人，每个工人有三个任务，2号任务的最大分配数为2。首先将个体C1中工人w11中的2号任务替换成小于最大分配数的3号任务，使任务2不超过最大分配数。接着检查每个工人是否有重复任务，并将工人w13中的5号任务替换成小于最大分配数的4号任务。

算法4是修复算子，首先统计个体中每个任务已分配的个数，计算每个任务剩余可分配的数量avnumj。接着将avnumj>0的任务替换掉avnumj<0的任务，使每个任务的avnumj≥0。最后对每个工人进行检查，用avnumj>0的任务替换片段中重复任务。

算法4 修复算子

输入：无效任务分配解Cinv。

输出：有效任务分配解Cv。

统计无效解Cinv中每个任务tj分配给工人的个数

将最大分配数减去已分配数，计算出每个任务tj剩余可分配数avnumj

找出avnumj<0的任务tinv

按序号用 avnumj>0的任务tv替换解中的任务tinv

更新每个任务tj的avnumj，使所有的avnumj≥0

对每个工人wi的任务分配片段进行检查，并记录有重复分配的任务

按序号选择avnumj>0的任务替换掉重复任务

return Cv

3 实验分析

实验在Windows 10操作系统、Intel Core i5-10200H 2.40 GHz CPU、16.0 GB内存的机器上运行，用MATLAB R2020b编写算法。本文选取三种多目标进化算法，分别为MOEADUR［22］、GFMMOEA［23］、DEAGNG［24］，来验证DCMEA算法的性能。其中MOEADUR和DEAGNG是基于分解的多目标进化算法，类似算法已经应用于MCS任务分配领域中［17］，GFMMOEA是近年来提出的较为先进的多目标进化算法。算法参数按照原文献设置，并添加了修复算子处理约束。

3.1 实验数据集及参数设置

实验采用Foursquare数据集［25］中纽约市9：00～12：00的签到数据进行任务分配的测试。Foursquare数据集包含了大约十个月从纽约市和东京市收集的签到记录，每次签到都包含以下记录：user ID、venue ID 、venue category ID、venue category name、latitude、longitude、timezone offset in minutes、UTC time。由于纽约市中签到地点存在较明显的冷热区，由此截取了经纬度范围为［-74.02，-73.92］、［40.68，40.8］，约15 km×10 km的长方形区域，并将数据集中签到记录的经纬度视为MCS中任务集的地点，为每个任务生成随机不同的tnummaxj数及skij值。此外选取不同ID工人初始签到的地点作为工人的初始时间地点进行任务分配测试，根据文献［20］随机生成信誉值Ri，同时将Gompertz函数的参数分别设为a=e/2、b=-1、c=-1，使工人信誉指数和任务熟练指数取值范围相近。为探寻在不同规模下算法的性能，选取了三组不同数量的工人任务实例集进行模拟，分别为data1：m=10，n=50；data2：m=20，n=100；data3：m=30，n=150。具体实验参数的值和范围见表1。

3.2 实验结果分析

1）解集分布

图8展示了DCMEA与对比算法在三个实例集上获得的MCS任务分配解集所对应的UW和UP值分布。结果显示，DCMEA明显优于对比算法，能够获得更高的求解精度。DCMEA的UW和UP值分布也更加均匀和广泛，因此能够为平台提供更加多元化的MCS任务分配方案。

2）IGD和HV指标

算法在实例上独立运行30次，得到反向世代距离（IGD）［26］和超体积（HV）［27］的平均值和标准差，如表2、3所示。表中括号的数字为标准差。IGD评价指标可以综合评价算法的收敛性和多样性，IGD指标越小，算法的收敛性和多样性越好。HV指标表示所获得的非支配解集在目标空间上的覆盖范围，HV值越大，说明算法的解集覆盖面越宽、分布越均匀，越接近真实Pareto前沿。

表2中，DCMEA的IGD平均值和标准差均优于其他四种对比算法，表明DCMEA求解任务分配模型能够获得优于对比算法的精度，同时在30次运行中得到的任务分配结果波动不大，因此具有更好的稳定性。从数据集data1到data3，随着实例复杂性增加，DCMEA的IGD值与其他算法的IGD差值越大。说明DCMEA随着实例复杂增加能够获取比其他算法更优的任务分配解集。表3显示DCMEA的HV平均值均优于对比算法，说明DCMEA得到的任务分配解集精度更高，且具有更好的多样性。同样，DCMEA随着实例复杂增加能够获取比其他算法更优的任务分配解集。

3）运行时间

算法在实例上独立运行30次，得到运行时间的平均值和标准差，如表4所示。DCMEA在较为复杂的实例data2和data3上运行时间为最短，在data1上的运行时间只比DEAGNG略长。说明DCMEA总体上运行时间短于对比算法，在解决复杂问题上更能显示其优势。

4）IGD和HV收敛曲线

图9、10展示了算法在data1上迭代5万次的IGD、HV的收敛曲线。DCMEA的收敛曲线在IGD上快速下降，并到达其他曲线下面，最终达到最小值。DCMEA的收敛曲线在HV上快速上升，并到达其他曲线上面，最终达到最大值。说明DCMEA的收敛速度明显快于对比算法，在迭代早期能较快地找到优秀的任务分配解集，且在迭代后期也不易陷入局部最优，最终收敛精度也优于其他算法。

上述实验验证了DCMEA在求解异构效用MCS任务分配问题具有优于对比算法的收敛精度、收敛速度和解的多样性。DCMEA表现更优的主要原因与算法设计所采用的技术有关。首先引入随机加权贪婪初始化策略，生成优势解来初始化种群，从而能够引导种群朝着最优解的方向进化。此外，随机的权重和任务分配顺序保证了初始种群的多样性。双种群竞争机制把种群划分为两个子种群，每个子种群根据不同的策略更新种群个体。能够在进化过程中保持种群的多样性，使得种群不易陷入局部最优，增加了种群的收敛性精度和速度。最后，算法中所设计的修复算子使无效解满足实际问题的约束条件，保留了其中的有用信息，进一步提升了种群的收敛性和多样性。

3.3 策略有效性分析

DCMEA结合本章MCS任务分配模型的特点，在进化算法的基础上设计了随机加权贪婪初始化、双种群竞争搜索以及修复算子等策略。其中修复算子使个体能够满足约束条件，随机加权贪婪初始化、双种群竞争搜索增强了算法的求解性能。为验证随机加权贪婪初始化策略和双种群竞争搜索策略对算法性能提升的有效性，将DCMEA中初始化策略改为随机初始化得到DCMEAR算法，同时将DCMEA改为在单种群上采用顺序交叉和两点交换得到SMEA算法，并与DCMEA进行对比。

1）解集分布

图11展示了在三个不同数据实例集上DCMEAR、SMEA和DCMEA获得的MCS任务分配解集所对应的UW和UP值分布。

结果显示，DCMEA在迭代过程中可以找到更加优越的解集。SMEA的解集分布差于另外两种算法，说明双种群竞争进化策略有效地改进了传统进化算法种群单一、容易陷入局部最优的问题。DCMEAR获得解集的UW和UP值随着数据实例集的增大越来越差，这表明随着任务分配的复杂度的逐渐增加，较好的初始解能够引导种群的搜索，增加算法的寻优性能。

2）IGD和HV指标

表5、6展示了三种算法IGD、HV指标的平均值和标准差，每个算法运行30次，优异的值加粗显示。可以看出，DCMEA的IGD、HV值优于其他对比算法，进一步表明DCMEA的改进策略有效地提升了求解任务分配模型的精度和性能。

3.4 模型有效性分析

本文综合考虑了工人的信誉异质性和不同工人对任务所需数据的熟练程度对任务分配的影响，结合信誉指数和任务熟练指数设计了异构效用机制。为说明异构效用机制对任务分配的影响，将本文模型与只考虑工人信誉和只考虑任务熟练程度的两种模型进行对比。图12展示了在data1上不同模型采用DCMEA算法生成的任务分配方案集的平均工人收益和平台收益。由图可知，本文模型能够找到UW和UP平均值更为均衡的方案，同时UW与UP值的和也略高于其他模型，验证了本文异构效用机制的有效性。

4 结束语

本文引入了信誉指数和任务熟练指数来描述工人和任务的异质性，构建了最大化工人异构效用和最大化平台异构效用的MCS多目标异构效用任务分配模型。为了求解该模型，通过引入随机贪婪初始化、双种群竞争进化、修复算子等技术设计了一种双种群竞争的多目标进化算法DCMEA。通过在解集分布、IGD和HV指標、运行时间上的实验，证明DCMEA能够在求解异构效用MCS多目标任务分配问题中获得良好的收敛精度、速度和稳定性，并且在复杂的环境中依然能够获得较好的任务分配结果。在后面的工作中，可以考虑在任务分配中对工人的位置进行隐私保护，减少工人参与任务的顾虑、激发积极性，从而可以招募到更多优质的工人。

参考文献：

［1］Guo Bin，Wang Zhu，Yu Zhiwen，et al.Mobile crowd sensing and computing：the review of an emerging human-powered sensing paradigm［J］.ACM Computing Surveys，2015，48（1）：1-31.

［2］Liu Yutong，Kong Linghe，Chen Guihai.Data-oriented mobile crowdsensing：a comprehensive survey［J］.IEEE Communications Surveys & Tutorials，2019，21（3）：2849-2885.

［3］Sun Wen，Li Qiang，Tham C K.Wireless deployed and participatory sensing system for environmental monitoring［C］//Proc of the 11th Annual IEEE International Conference on Sensing，Communication，and Networking.Piscataway，NJ：IEEE Press，2014：158-160.

［4］Coric V，Gruteser M.Crowdsensing maps of on-street parking spaces ［C］//Proc of IEEE International Conference on Distributed Computing in Sensor Systems.Piscataway，NJ：IEEE Press，2013：115-122.

［5］Guo Bin，Chen Huihui，Yu Zhiwen，et al.FlierMeet：a mobile crowdsensing system for cross-space public information reposting，tagging，and sharing［J］.IEEE Trans on Mobile Computing，2015，14（10）：2020-2033.

［6］Alemdar H，Ersoy C.Wireless sensor networks for healthcare：a survey［J］.Computer Networks，2010，54（15）：2688-2710.

［7］Capponi A，Fiandrino C，Kantarci B，et al.A survey on mobile crowdsensing systems：challenges，solutions and opportunities［J］.IEEE Communications Surveys & Tutorials，2019，21（3）：2419-2465.

［8］Zhang Lichen，Ding Yu，Wang Xiaoming，et al.Conflict-aware participant recruitment for mobile crowdsensing［J］.IEEE Trans on Computational Social Systems，2020，7（1）：192-204.

［9］Ni Jianbing，Zhang Kuan，Xia Qi，et al.Enabling strong privacy pre-servation and accurate task allocation for mobile crowdsensing［J］.IEEE Trans on Mobile Computing，2020，19（6）：1317-1331.

［10］Song Zheng，Liu Chiharold，Wu Jie，et al.QoI-aware multitask-oriented dynamic participant selection with budget constraints［J］.IEEE Trans on Vehicular Technology，2014，63（9）：4618-4632.

［11］Wang Jiangtao，Wang Yasha，Zhang Daqing，et al.Fine-grained multi-task allocation for participatory sensing with a shared budget［J］.IEEE Internet of Things Journal，2016，3（6）：1395-1405.

［12］Li Xin，Zhang Xinglin.Multi-task allocation under time constraints in mobile crowdsensing［J］.IEEE Trans on Mobile Computing，2021，20（4）：1494-1510.

［13］Ji Jianjiao，Guo Yinan，Gong Dunwei，et al.Evolutionary multi-task allocation for mobile crowdsensing with limited resource［J］.Swarm and Evolutionary Computation，2021，63：100872.

［14］蔣伟进，张婉清，陈萍萍，等.基于IWOA群智感知中数量敏感的任务分配方法［J］.电子学报，2022，50（10）：2489-2502.（Jiang Weijin，Zhang Wanqing，Chen Pingping，et al.Quantity sensitive task allocation method based on IWOA in group intelligence perception［J］.Acta Electronica Sinica，2022，50（10）：2489-2502.）

［15］杨桂松，吴笑天，高丽，等.面向单任务质量保障的移动群智感知任务分配［J］.计算机工程，2022，48（9）：45-54.（Yang Guisong，Wu Xiaotian，Gao Li，et al.Task allocation towards individual task quality assurance in mobile crowd sensing［J］.Computer Enginee-ring，2022，48（9）：45-54.）

［16］Estrada R，Mizouni R，Otrok H，et al.A crowd-sensing framework for allocation of time-constrained and location-based tasks［J］.IEEE Trans on Services Computing，2020，13（5）：769-785.

［17］Ji Jianjiao，Guo Yinan，Gong Dunwei，et al.MOEA/D-based participant selection method for crowdsensing with social awareness［J］.Applied Soft Computing，2019，87：105981.

［18］Li Mingchu，Gao Yuan，Wang Mingliang，et al.Multi-objective optimization for multi-task allocation in mobile crowd sensing［J］.Procedia Computer Science，2019，155：360-368.（下轉第169页）

（上接第164页）

［19］Shen Xiaoning，Chen Qingzhou，Pan Hongli，et al.Variable speed multi-task allocation for mobile crowdsensing based on a multi-objective shuffled frog leaping algorithm［J］.Applied Soft Computing，2022，127：109330.

［20］Ren Ju，Zhang Yaoxue，Zhang Kuan，et al.SACRM：social aware crowdsourcing with reputation management in mobile sensing［J］.Computer Communications，2015，65：55-65

［21］Wu Shengnan，Wang Yingjie，Tong Xiangrong.Multi-objective task assignment for maximizing social welfare in spatio-temporal crowdsour-cing［J］.China Communications，2021，18（11）：11-15.

［22］De Farias L R C，Araújo A F R.A decomposition-based many-objective evolutionary algorithm updating weights when required［J］.Swarm and Evolutionary Computation，2022，68：100980.

［23］Tian Ye，Zhang Xingyi，Cheng Ran，et al.Guiding evolutionary multi-objective optimization with generic front modeling［J］.IEEE Trans on Cybernetics，2020，50（3）：1106-1119.

［24］Liu Yiping，Ishibuchi H，Masuyama N，et al.Adapting reference vectors and scalarizing functions by growing neural gas to handle irregular pareto fronts［J］.IEEE Trans on Evolutionary Computation，2020，24（3）：439-453.

［25］Yang Dingqi，Zhang Daqing，Zheng V W，et al.Modeling user activity preference by leveraging user spatial temporal characteristics in LBSNs［J］.IEEE Trans on Systems，Man，and Cybernetics：Systems，2015，45（1）：129-142.

［26］Bosman P，Thierens D.The balance between proximity and diversity in multi-objective evolutionary algorithms［J］.IEEE Trans on Evolutionary Computation，2003，7（2）：174-188.

［27］Zitzler E，Thiele L.Multi-objective evolutionary algorithms：a comparative case study and the strength pareto approach［J］.IEEE Trans on Evolutionary Computation，1999，3（4）：257-271.