一种基于荧光信息导航的聚类算法

王跃飞 曾世杰 于曦 刘兴蕊 李越

摘 要：聚类是无监督机器学习算法的一个分支，它在信息时代具有广泛的应用。然而，在多样化的聚类算法研究中，常存在密度计算需要指定固定的近邻数、需要提前指定簇数目、需要多次迭代完成信息叠加更新等问题，这些问题会让模型丢失部分数据特征，也会加大计算量，从而使得模型的时间复杂度较高。为了解决这些问题，受萤火虫发光和光信息传递、交流的启发，提出了一种萤光信息导航聚类算法（firefly luminescent information navigation clustering algorithm，FLINCA）。该方法由腐草生萤和聚萤成树两大模块构成，首先将数据点视作萤火虫，并采用自适应近邻数的方式确定萤火虫亮度，通过亮度完成萤火虫初步聚类，然后再根据萤火虫树进行簇融合，完成最终聚类。实验证明，与12种不同的算法进行对比，FLINCA在4个聚类benchmark数据集和3个多维真实数据集上表现出较好的聚类效果。这说明基于萤火虫发光和光信息传递的FLINCA算法在聚类问题中具有广泛的应用价值，能够有效解决传统聚类算法中存在的问题，提高聚类结果的准确率。

关键词：无监督聚类； 仿生学； 萤火虫算法

中图分类号：TP301.6   文献标志码：A   文章编号：1001-3695（2024）01-018-0116-10

doi：10.19734/j.issn.1001-3695.2023.05.0185

Firefly luminescent information navigation clustering algorithm

Abstract：Clustering is a branch of unsupervised machine learning algorithms that has widespread applications in the information age. However， diverse research on clustering algorithms often faces issues such as it need to specify a fixed number of neighbors for density calculation， the requirement of predefining the number of clusters， and the necessity for multiple iterations to update information aggregation. These problems can lead to the loss of data features and increase computational complexity， resulting in higher time complexity of the models. To address these challenges， this paper inspired by the luminescence and light information transmission of fireflies and proposed a clustering algorithm called FLINCA. FLINCA consisted of two main modules， such as growing fireflies and merging fireflies trees. Firstly， it treated data points as fireflies， and determined their brightness using an adaptive number of neighbors to achieve preliminary clustering. Then， it performed cluster fusion based on the firefly trees， resulting in the final clustering outcome. Experimental results demonstrate that FLINCA exhibits favorable clustering performance on four benchmark clustering datasets and three real-world multidimensional datasets compared to twelve different algorithms. This confirms the extensive applicability of FLINCA， which is based on firefly luminescence and light information transmission， in addressing the limitations of traditional clustering algorithms and improving clustering accuracy.

Key words：unsupervised clustering; bionics; firefly algorithm

0 引言

近年來，随着数据的大规模增加，机器学习大量应用于人们的生活中，其中聚类作为无监督算法，它能在不需要标签的情况下，将一组数据对象按照相似性或距离的度量值划分为不同的组，使得同一组内的数据对象相似性较高，而不同组之间的相似性较低。作为机器学习领域的核心研究问题之一，它在自然科学和社会科学领域有大量的聚类应用［1～4］，如文本分析［5］、基因组学分析［6］、MRI图像分析［7］、遥感图像［8］。随着机器学习技术的发展，在各种思想的启发下，聚类演化出不同的算法策略，形成了多种高效算法，丰富了机器学习的技术框架，提高了数据挖掘的学习效率。因此，大量的学者对聚类技术进行了长期的研究，诞生了不同的数据特征捕捉方法和不同的学习策略。

在数据特征捕捉上，近年来有很多出色的无监督算法从不同角度对点关系进行了分析。文献［9］提出了一种TWO-NN的新型数据集内在维度估计方法，该方法只需计算样本与第一个近邻和第二个近邻的距离差，可以减少曲率、密度变化的影响，以及降低由此产生的计算成本。文献［10］提出了一种PAk方法来计算化学分子体系的自由能，在该方法中每个样本可以获得自己的自适应近邻数，从而能够更好地分析数据密度关系。文献［11］则分析了聚类簇中孤立点的关系，提出了ODIC-DBSCAN算法，解决了当聚类后簇的数目低于实际数目，或孤立点被伪装在簇内的情况下，簇内孤立点的判定则会更加困难的问题。

在对应的学习策略中，主流的聚类算法可以分为基于消息传递聚类、分区聚类、分层聚类和密度聚类的方法。在基于消息传递聚类的聚类算法中，具有代表性的有affinity propagation算法［12］。该算法利用了图模型中的信息传递原理，将聚类过程视为一种消息传递过程。在该过程中，每个数据点将信息传递给其他数据点，以便更好地确定它们之间的相似性，从而完成聚类。在分区聚类中，具有代表性的有K-means++和mini-batch K-means算法［13，14］。K-means++算法利用一种新的种子点选择方法，即按照概率分布选择种子点，以便更好地初始化聚类中心，并在随后的聚类迭代中取得更快的收敛速度和更优的聚类结果。mini-batch K-means则将数据集划分为多个子集，从而提升算法在大规模数据集上的聚类速度。在分层聚类中，具有代表性的有agglomerative clustering和BIRCH算法［15，16］。这类算法往往通过自底向上或自上向下的方式进行簇融合或者簇分裂，从而完成聚类。在密度聚类中，具有代表性的有DBSCAN和OPTICS算法［17，18］。其中DBSCAN算法将簇定义为一组在高密度区域内紧密相连的点，通过密度完成聚类，并且能够自动消除噪声和孤立点。而OPTICS算法通过定义可达距离来评估每个数据点的密度，通过基于这个距离的排序，可以在不知道聚类数量的情况下发现聚类结构。由这些方法衍生出来的算法大大丰富了聚类的多样性，提高了聚类效果。

此外，还有很多基于仿生学的聚类方法如基于粒子群、蚁群等［19～22］。在基于仿生学的聚类算法中，firefly algorithm（FA）是基于萤火虫集群的优化算法［23］，它根据萤火虫的亮度、吸引度实现目标优化，因此需要一定数据进行预训练得到簇中心，然后将数据分配到指定的簇上。类似的还有，Xie等人［24］通过矩阵替代吸引力系数，提出了用于解决初始化參数敏感的IIEFA（inward intensified exploration firefly algorithm）模型和解决局部最优的CIEFA（compound intensified exploration firefly algorithm）模型。具体而言，该方法首先使用改进的萤火虫算法确定聚类中心的初始值，并使用K-means算法进行进一步的优化。改进的萤火虫算法使用自适应参数来调整初始萤火虫位置和发光强度，以避免陷入局部最优解。此外，该方法还利用了改进的局部搜索策略，从而可以更加有效地搜索最优解。此外，Banu等人［25］提出了fuzzy firefly clustering（FFC）算法，该方法结合模糊萤火虫聚类和改进的遗传算法，以更准确地分析肿瘤数据，并从中提取有用的信息。这些受仿生学启发的思想都极大地丰富了聚类算法，并给其应用带来了启发。

整体而言，虽然目前的聚类算法都在生活中具有广泛的应用，但它们往往有共同的不足之处，这也属于目前聚类研究需要迫切解决的问题：a）部分聚类算法在计算点密度时，往往需要指定近邻数目，固定的近邻数目可以较好地捕捉局部特征，但难以捕获全局特征;b）有些聚类算法在聚类前需要事先指定聚类的数量，而在实际应用中往往很难提前知道簇的数目，因此参数的选择对聚类结果有一定的限制;c）基于仿生学的聚类算法往往需要通过多次迭代实现信息素的更新，从而得到稳定的聚类结果，然而，这种迭代往往会消耗大量的运行时间，并且聚类结果不一定收敛。

即使上述问题较为棘手，但通过仿生学可以为解决这类问题提供较好的启发。因此，考虑到自然界中萤火虫具有集群生活的习性，本文提供了以下研究动机：

a）萤火虫发光：萤火虫具有生物发光的能力，并且萤火虫族群中第一个发光的萤火虫通常被称为“引领萤火虫”。它能通过自身发光来引导其他成员在特定的时间和空间内发光，帮助其他成员在同步发光的过程中保持一定的节奏和规律，在萤火虫族群中起到了引导和协调的作用。此外，萤火虫的亮度一般只与自身相关，每只萤火虫具有不同的亮度。该启发在聚类中可以被应用为计算不同点的密度时，需要采用不同的近邻数，后续实验也证明这样计算的密度更能体现集群智慧，具有更好的聚类效果。

b）发光频率：萤火虫可以通过发光信号来识别自己的同种群体，并区分其他物种或者其他族群，用于传递信息的萤火虫一般被称为“信使萤火虫”。这有助于萤火虫族群在复杂的环境中识别和选择合适的伴侣进行繁殖。因此在聚类算法中可以参考发光频率完成聚类，如果点与点之间的发光频率接近，则说明很可能属于同一个簇，这样聚类不需要提前指定簇数目。此外，由于萤火虫的发光频率是固定的，在初始化时便能确定每一只萤火虫的发光频率，所以该算法不需要迭代累加信息素，从而减少了运行时间。

为了填补上述聚类算法的局限性，本文提出了一种新型基于仿生学的萤火虫聚类算法——萤光信息导航聚类算法（firefly luminescent information navigation clustering algorithm，FLINCA）。

1 算法模型

1.1 模型总览

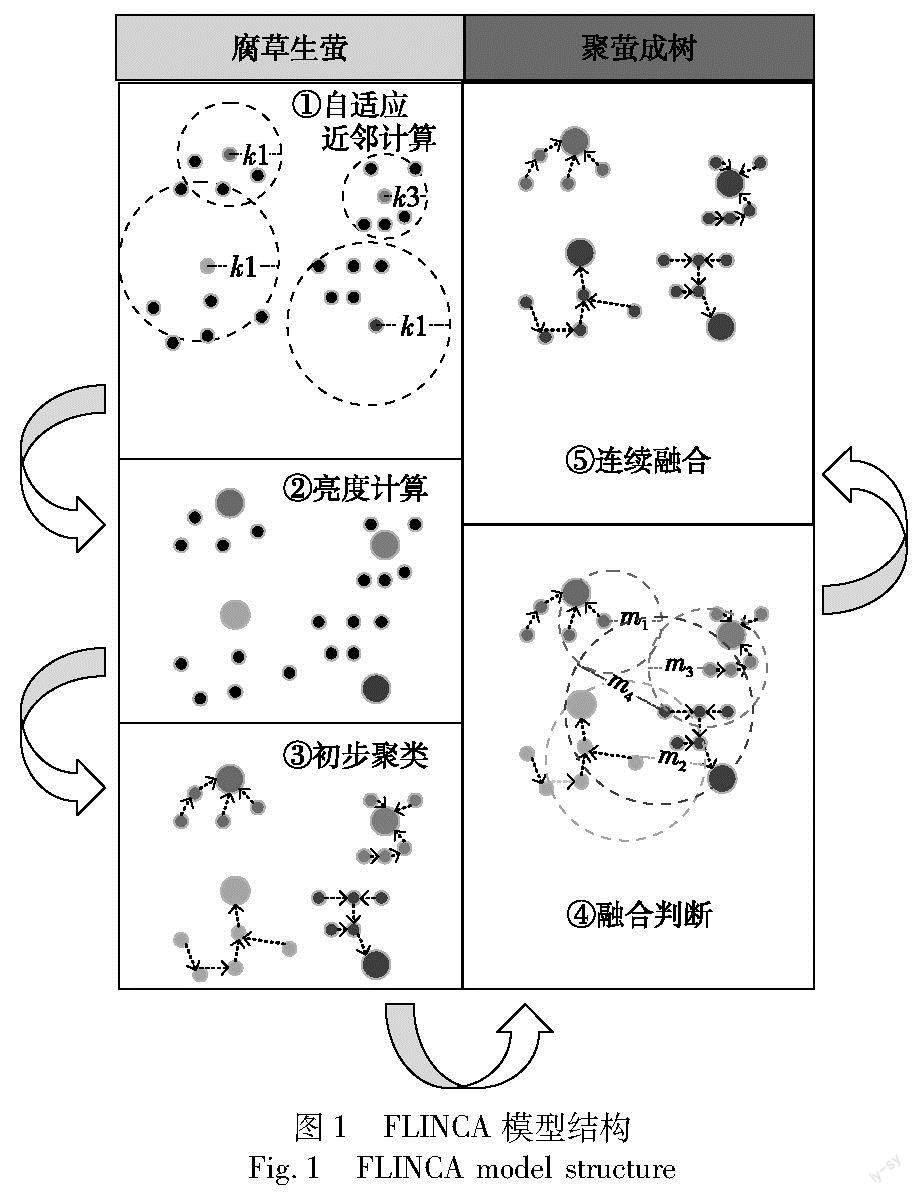
如图1所示，FLINCA主要由腐草生萤和聚萤成树两大模块构成。其中腐草生萤模块包含自适应近邻计算、亮度计算、初步聚类三个子模块，在该模块中会先根据数据的分布情况和用户传入的参数，把每个数据作为一只萤火虫，初始化每只萤火虫的亮度、自适应近邻数，然后将萤火虫按照亮度由高到低排列，每只萤火虫选择最近的一只亮度比自身高的萤火虫作为向导，将自身归属到向导簇，从而完成初步聚类。聚萤成树模块包含融合矩阵、连续合并两个模块，在该模块中会根据初步聚类的情况进行簇合并，从而完成最终的聚类。由于每个萤火虫对应族群就像一棵树，两个簇合并成为新簇可以看做两棵萤火虫频率树合并成为一棵新萤火虫频率树，所以这一部分叫“聚萤成树”。

1.2 腐草生萤：初始化萤火虫亮度

1.2.1 自适应近邻计算

对于传入的数据集Data，存在一系列独立同分布的向量点{xi，…，xN}，每个点可以视作一只萤火虫。对于数据集Data中任意的点xi、xj都存在欧氏距离Disi，j，如式（1）所示。

Disi，j=Disj，i=‖xi－xj‖2 xi，xj∈Data（1）

欧氏距离可以衡量数据之间的相似度，一般来说欧氏距离越大，数据相似度越低。通过欧氏距离可以较好地捕捉数据空间中点的局部密度分布情况，但不便于捕捉全局密度，而不适用于高维数据集。为了解决这些问题，本文优化了数据间的度量方法，参考文献［10］，本文也通過数据集的内在维度来更好地衡量数据间的相似性并将自适应近邻应用于萤火虫体系上。本文采用TWO-NN［9］的方法计算数据集的内在维度，对于任意规模的数据集都存在内在维度D，其小于数据集特征数，但却能代表大部分数据的分布情况。通过计算内在维度，可以让模型捕捉更多有用的特征，并且减少计算量。

ri，j=rj，i=DisDi，j=DisDj，i（2）

如式（2）所示，定义ri，j表示数据xi、xj之间的相异度，其中D为数据集Data的内在维度，ri，j越大，表示xi、xj之间的差异越大。为了更好地捕捉数据点的分布情况，密度计算被考虑到了算法中。为了计算密度，则需要考虑数据点的近邻信息。为了更快速地获取到数据点与近邻之间的距离，本文采用了KD-Tree方法。在计算近邻信息后，可以获得点xi的前k个近邻点对应的相异度序列{ri，j}l≤k，其中ri，1表示点xi与第一近邻的相异度，ri，2表示点xi与第二近邻的相异度，依此类推。此外，由于ri，0表示点xi与自身的相异度，所以ri，0=0。

考虑到近邻之间的距离差有助于从全局的角度衡量数据分布，因此定义截断距离v如式（3）所示。

vi，l=ω×（ri，l－ri，l－1）（3）

其中：ω为传入参数，用于放大距离差、扩大差异，由于该变量不对方程起约束作用，所以属于自由变量。文献［9］证明，在数据集密度连续时，截断距离v服从参数为ρ的指数分布，如式（4）所示。

f（v）=ρ×e－ρ×v（4）

因此可以对点xi与周围近邻的距离进行似然估计，为了求似然估计，这里对指数分布取对数，可得

ri，l=log（vi，l）=log（ρi×e－ρi×vi，l）=log（ρi）－ρi×vi，l（5）

数据点xi与其周围k个近邻对应的密度似然估计函数如式（6）所示。

其中：Vi，k为点xi与周围k个近邻的截断距离之和。

为求参数ρi的最大似然估计，现将式（6）对ρi求导，则有

现已知点xi的密度ρi可以根据其对应的k个近邻进行似然估计，可见随着k的增加，误差的变化并不一定固定，这主要是由于数据集的密度分布并不一定平均，所以也就存在着数据点xi的密度和第k+1个点的密度相同或者不同两种情况。为了找到每个点的自适应k，现有两种k自适应模型。

k自适应模型1 当点xi的密度和其对应的第k+1个近邻的密度不同时，记点xj为点xi的第k+1个近邻，则点xi与xj的最大似然估计密度之和如式（8）所示。

k自适应模型2 当点xi的密度和其对应的第k+1个近邻的密度相同时，记点xj为点xi的第k+1个近邻，则点xi与xj的最大似然估计密度之和如式（9）所示。

为了综合衡量LM1和LM2对于模型的影响，本文采用了似然比检验的方法，得出综合模型Dk，如式（10）所示。

Dk=－2（LM1－LM2）=－2k［log（Vi，j）+log（Vj，k）－2log（Vi，k+Vj，k）+log（4）］（10）

由于LM1和LM2都与k相关，而且k符合正态分布，所以Dk符合自由度为1的卡方分布。随着k的增加，对应Dk越大，说明对于k的最大似然估计置信度越高。所以可以记点xi的最大似然估计近邻数为k^，通过查表可以找到对应的置信度。比如当Dk=3.841时，查卡方分布表则可知有95%的把握判定点xi的最大近邻数为k^。

为了自适应获得每个点对应的最大似然估计近邻数为k^，可以设置阈值Dthr，使得k^满足

（Dk

式（11）表示算法将从第一个近邻开始遍历，将当前最大似然估计近邻数记作k^，假设存在一个k≤k^使得Dk

1.2.2 亮度计算

有了最大似然估计近邻数，则可以求出对应的点密度，考虑到预测误差带来的影响，预测误差越大，说明对应结果越不稳定，因此萤火虫亮度与其成反比例。定义萤火虫亮度计算方法为

萤火虫亮度计算对应的伪代码如算法1所示。在该算法中，时间消耗主要来源于KD树的索引构建和最大似然估计k的预测，其中KD树索引构建的算法时间复杂度为O（K×N×log（N）），K为数据集维度，N为数据集规模。在进行k的最大似然估计时，需要遍历每一个点，然后将k从1开始遍历，直到k符合阈值条件。为了防止模型发散，使用max_k作为k逾值的约束，一旦遍历时k超过了max_k则停止遍历，将max_k作为最大似然估计近邻，因此这一块的算法时间复杂度为O（N×max_k）。因此，腐草生萤模块的算法时间复杂度为O（max（K×N×log（N）， N×max_k））。

该算法在进行亮度计算模块时，首先需要采用TWO-NN的方法计算数据集的内在维度，然后通过KD树构建近邻矩阵，通过近邻矩阵对应的距离矩阵计算相异性矩阵，随后初始化点的近邻和阈值判断信息，开始遍历数据集中每一个点直到遍历完所有点，对每次遍历对应的k进行最大似然估计，依照式（10）得到似然比综合模型Dk和Dk1，并判断综合模型与阈值的关系，如果达到最大似然近邻k^则停止，保存相关信息。

算法1 萤火虫亮度计算

输入：数据集data、置信阈值Dthr、差异放大系数omega、最大近邻限度max_k。

输出：每个点的自适应近邻k、密度rou、误差error、亮度light、距离矩阵distances、近邻矩阵indices。

id=twoNN（data）.intrinsic_dim       //计算内在维度

tree=KDTree（data）            //构建KD樹

dis，ind=tree.query（data，k=min（max_k， data.shape［0］））

//查找近邻

dissimilarity=np.power（dis，id）      //获取相异度

V_matrix=np.diff（dissimilarity， axis=1）×omega

//计算截断距离

list_k，list_rou，list_error，list_light=Init（）

//初始化每个点对应的k

for i in range（len（data））：         //遍历每一个点

Dk_flag=false       //判断是否有点满足密度差条件

now_k=0                //当前近邻数

while True：

now_k+=1               //更新now_k

j=indices［i］［now_k］   //找到当前点的第k个近邻

Dk，Dk1=caculation（i， V_matrix，now_k） //计算Dk和Dk1

if Dk

Dk_flag=true

if （（Dk1>=Dthr） and （Dk_flag==true）） or （now_k==max_k-1）：

//阈值判断

存储近邻、密度、误差、亮度

break

return list_k， list_rou， list_error， list_light， distances， indices

1.2.3 初步聚类

在得到每个点对应的亮度和最大似然估计近邻后，可以对数据集进行初步聚类，为了更好地完成聚类，在参考萤火虫的集群特性后，定义萤火虫的三种身份如下：

定义1 如果萤火虫xi周围的k^个最大似然估计近邻的亮度都小于xi对应的亮度Lighti，则可以认为Lighti为亮度高峰，萤火虫xi为引领萤火虫。

定义2 如果萤火虫xi周围的k^个最大似然估计近邻中，存在萤火虫xj的亮度Lightj大于xi对应的亮度Lighti，则萤火虫xi的归属簇与萤火虫xj的归属簇相同，记萤火虫xj为萤火虫xi的向导萤火虫。

定义3 如果萤火虫xi没有成为任一其他萤火虫的向导萤火虫，则记萤火虫xi为信使萤火虫。

如图2（a）所示，在萤火虫xi的k近邻范围内，如果不存在比萤火虫xi亮度更高的萤火虫，则记萤火虫xi为引领萤火虫。因此，该萤火虫在聚类中的作用类似于局部簇心，通过引领萤火虫可以向外传播光芒，吸引其他萤火虫加入和自身相同的归属簇。如果其他萤火虫与引领萤火虫数同一簇，则认为这些萤火虫发出相同频率的光芒。

如图2（b）所示，在萤火虫xm的k近邻范围内，存在比萤火虫xm亮度更高的萤火虫xi，则记萤火虫xi为萤火虫xm的向导萤火虫。该萤火虫既被其他萤火虫吸引，和亮度比它大的萤火虫归属于同一簇，发出相同频率的光，同时也吸引着其他亮度比它小的萤火虫，让其也发出相同频率的光芒。因此，它的主要功能是作为亮度更小萤火虫的向导，传播自己所在簇的标签。

如图2（c） 所示，在该分布中，萤火虫xi为引领萤火虫，萤火虫xi和萤火虫xm都为向导萤火虫，萤火虫xn因为没有成为任一萤火虫的向导，所以它为信使萤火虫。信使萤火虫只会被亮度比自己更高的萤火虫吸引，不会吸引其他萤火虫，但它却能作为信使，与其他簇的萤火虫进行沟通。因此它的主要作用是传递信息，判断簇与簇之间是否需要融合。

此外，本文使用树的数据结构来保存这一关系，具体而言，属于同一个簇的萤火虫被认为发出相同频率的光芒，这些萤火虫也将作为节点被存储在同一棵树上，这个树就是该簇的同频树。假设图2（c）对应同频树treei，则在同频树treei中，萤火虫xi为根节点，萤火虫xm为萤火虫xi的子节点，萤火虫xn为萤火虫xm的子节点，同时也是同频树treei的叶子节点。

在完成亮度计算后，需要将萤火虫按照亮度降序排序，然后根据亮度由高到低，依次遍历每一只萤火虫。对于被遍历的萤火虫而言，它需要根据对应的自适应近邻数k^，遍历每一个近邻，并且判断近邻亮度和自身亮度的关系，从而为萤火虫分配对应的身份，并且完成初步聚类。需要注意的是，在初步聚类的过程中算法并不需要迭代，且不具备随机性，因此能够保证每次运行得到的结果具有稳定性，这也是FLINCA相较于部分需要迭代的仿生学聚类算法更具有优势的原因之一。

如果存在近邻，其亮度高于或等于当前遍历萤火虫的亮度，则可以认为当前遍历的萤火虫失去作为引领萤火虫的机会，只能作为向导萤火虫或信使萤火虫，如定义2和3，此时，亮度比当前遍历萤火虫高的近邻会作为向导萤火虫，如定义2。由于向导萤火虫必定已被分配标签，所以向导萤火虫可以将同样的标签传递给当前遍历的萤火虫，使其发出和自身一样颜色的光，归属于同一个簇。与此同时，由于向导萤火虫存在同频树，所以需要将当前遍历的萤火虫加入到与向导萤火虫一样的同频树中，表示向导萤火虫和当前遍历的萤火虫发出同样频率的光芒，这有利于后续“聚萤成树”模块的簇融合。

如果所有近邻的亮度都低于当前遍历的萤火虫亮度，则可以认为当前遍历的萤火虫是所有近邻中亮度最高的萤火虫，因此可以将其视作局部簇心，这样的萤火虫在定义1中也被称作引领萤火虫。在生成引领萤火虫时，需要对其分配一种新的光芒，即一个新的归属簇序号，在后续遍历其他萤火虫时，该萤火虫有机会成为向导萤火虫，从而将其簇序号分配给其他萤火虫，完成局部聚类，这也是整个算法的初步聚类。与此同时，它也将作为根节点，生成一棵新的同频树，后续如果该引领萤火虫作为其他萤火虫的向导，则将其他萤火虫加入到这棵同频树中。

整体而言，腐草生萤模块通过判断每个点与其对应的自适应近邻点的亮度关系来确定对应身份，从而更好地捕捉点与自适应近邻点之间的数据特征。这种方法相较于传统算法中仅依赖距离、固定近邻密度等数据特征衡量的方法，具有更高的灵活性和可适用性。

算法2 初步聚类（萤翅流光模块）

输入：每个点的自适应近邻k、密度rou、误差error、亮度light、距离矩阵distances、近邻矩阵indices。

输出：初始聚类结果label、同频簇树列表sync_tree_list。

sync_tree_list=［］  //存储同频树，每棵同频树表示一个簇

label=［-1］×data.shape［0］      //初始化标签

label_index=0        //使用的标签序号

sorted_list_light_id=sort（list_light）

//对萤火虫亮度进行降序排序O（N log N）

for i in range（0， len（sorted_list_light_id））：

//根据亮度从高到低遍历每一个点i

leading_firefly_flag=true     //引领萤火虫标签

for j in range（1， list_k［sorted_list_light_id［i］］）：

//遍历该点的近邻j

hlp=indices［sorted_id［i］］［j］

//记当前近邻为亮度更高点

if list_light［hlp］>list_light［sorted_id［i］］：

//判断亮度

leading_firefly_flag=false

break

if leading_firefly_flag==True：

//如果当前点是引领萤火虫

leading_firefly.append（sorted_list_light_id［i］）

//引领萤火虫list添加当前点

label［sorted_list_light_id［i］］=label_index

//引领萤火虫生成新label

tree=Tree（）

//引领萤火虫生成同频树，树的根节点是该萤火虫

把当前点加入到同频树中

sync_tree_list.append（tree）

//把当前树加入到树list里面

label_index+=1        //更新标签序号

else：        //如果当前点不是引领萤火虫

把当前点加入对应的同频树里

更新标签

return label， sync_tree_list

从算法2可以看出，萤火虫一边进行聚类，一边生成同频树。具体而言，首先需要对萤火虫按照亮度进行降序排序，这时时间复杂度为O（N×log（N）），其中N为数据集规模。然后按照亮度由高到低依次遍历每一只萤火虫，遍历当前萤火虫的每一个近邻，如果近邻萤火虫的亮度高于当前萤火虫的亮度，那么可以认为近邻萤火虫是当前萤火虫的向导。既然当前萤火虫存在向导，则它不可能是引领萤火虫，那么它所归属的簇即为向导萤火虫归属的簇，同时将向导萤火虫作为自己的父节点，将自身作为新的节点加入到向导萤火虫存在的同频树中。如果当前萤火虫不存在向导萤火虫，则说明它是引领萤火虫，那么它会引领一个新的簇，同时自己作为根节点加入到新的同频树中。在进行簇分配和同频树生成时仅需遍历每一个点及其相关近鄰，近邻时间复杂度为O（N×k），其中k为每个点对应的近邻数。由于近邻数k远小于log（N），所以该模块的时间复杂度为O（N×log（N））。

1.3 聚萤成树：簇合并

1.3.1 融合判断

通过聚萤成树模块可以获得初步聚类的簇，聚萤成树模块将对这些簇进行合并，完成最终聚类。簇的合并主要依据频率差FG，它将对不同频率树的同频数进行限制，现对频率树的同频数定义如下：

定义4 如果萤火虫xi为频率树treei的叶子节点，萤火虫xi的k^个近邻中，如果存在m个萤火虫xj，且萤火虫xi和xj对应的簇不同，分别为i和j，那么频率树treei和treej之间的同频数为m。频率数越高，表示两个簇合并的可能性越大。

如果频率树treei只与频率树treej、treek之间存在同频数m、n，且m>n，若此时通过传参得到的频率差为FG，且有m-mFG，则表示频率树treei要与频率树treej却不与频率树treek融合；只有m-m

算法3 聚萤成树

输入：同频簇列表sync_tree_list，引领萤火虫列表l_firefly，旧标签label，频率差阈值FG。

输出：每个点对应标签label。

merge_array=np.zeros（［len（l_firefly），len（l_firefly）］）

//初始化融合矩阵。

for i in range（0，len（l_firefly））：

//遍历每个引领萤火虫

m_firefly_i=sync_tree_list［i］.leaves（）

//找到信使萤火虫节点

m_firefly_list_i=［］

for m_firefly in m_firefly_i：

//查询对应信使萤火虫

m_firefly_list_i.append（m_firefly.data）

m_firefly_set_i=set（m_firefly_list_i）

for j in m_firefly_set_i：

//遍历每一个信使萤火虫

for k in indices［j］［：list_k［j］］：

//遍历信使萤火虫的近邻

if label［l_firefly［i］］！=label［k］：

//如果近邻的簇和信使的簇不同

merge_array［label［l_firefly［i］］］［label［k］］+=1

merge_array［label［k］］［label［l_firefly［i］］］+=1

merge_list=［］  //从融合矩阵中提取出需要合并的簇

visited_list=［0］×len（l_firefly） //判断哪些簇已经被遍历了

for i in range（0，len（l_firefly））：

//遍历每个簇，递推得到需要连续合并的簇

if visited_list［i］==1：

continue

now_merge_list=［］

now_merge_list，visited_list=find_merge_center（FG， now_merge_list， visited_list， merge_array， i）

//递推找连续合并簇

merge_list.append（now_merge_list）

new_label=［0］×len（l_firefly）

for i in range（0，len（merge_list））：

//通过字典的形式存储每个旧簇对应的新簇序号

for j in merge_list［i］：

new_label［j］=i       //将旧标签与新标签对应

for i in range（0，data.shape［0］）：   //更新簇，完成合并

label［i］=new_label［label［i］］

return label

结合算法3可知，在聚萤成树模块中，首先需要初始化融合矩阵merge_array，其中每个单元格表示两个簇的同频数（定义4）。比如merge_array［0］［1］=10，则表示0号频率树与1号频率树的同频数为10，也意味着0号簇与1号簇有10个单位的可能性合并。最后需要遍历每一个引领萤火虫，找出每个引领萤火虫对应的频率树的叶子节点，即信使萤火虫。最后通过信使萤火虫进行信息交换，找到其他簇与当前簇的同频数，更新融合矩阵merge_array。

1.3.2 连续合并

考虑到簇合并具有连续性，比如簇C1可以与簇C2合并，簇C2可以和簇C3合并，那么可以认为簇C1也可以和簇C3合并。因此，需要通过递推的方式完成簇融合，这里调用find_merge_center函数来找到需要连续合并的簇，find_merge_center函数如算法4所示。

算法4 find_merge_center

输入：频率差阈值FG，連续合并列表merge_list，已访问列表visited_list，融合矩阵merge_array，当前访问位置now_p。

输出：连续合并列表merge_list，已访问列表visited_list。

if visited_list［now_p］==1：

//如果当前位置已经被访问则跳过

return merge_list，visited_list

merge_list.append（now_p）  // merge_list添加当前簇

visited_list［now_p］=1      //记录当前簇已被访问

res=np.where（merge_array［now_p］！=0）［0］

//获取与当前簇有同频萤火虫的簇序号

max_sync_firefly=max（merge_array［now_p］）

//获得最多的同频萤火虫

if len（res）<=0：      //如果没有同频萤火虫则返回

return merge_list，visited_list

else             //如果有同频萤火虫

for i in res：      //遍历每个可能同频簇的序号

if max_sync_firefly-merge_array［now_p］［i］ <= FG

//簇合并

merge_list.append（i）    //merge_list添加同频簇

merge_list，visited_list=find_merge_center（FG， merge_list， visited_list， merge_array， i）

//通過同频簇递推去找更多的同频簇

return list（set（merge_list）），visited_list

在算法4中，首先需要对融合矩阵merge_array中的now_position行进行判断，如果该行已经被遍历过了则跳过该行，如果没被遍历过，则继续后续流程。首先将now_position行标记为已遍历，将该行加入到连续合并列表merge_list里。之后获取融合矩阵merge_array的now_position行中数值大于0的列，并且返回列号。之后判断对应单元格数值与该行中最大的单元格数值之差，如果差别小于FG，则认为这两个簇可以合并，反之则不能。如果在遍历簇i对应的i行时，发现簇i和簇j能够合并，那么递推遍历簇j对应的合并列号，直到所有递推完成。

聚萤成树模块中的时间消耗主要来源于融合矩阵merge_array的更新。在融合矩阵merge_array的更新中，首先需要通过引领萤火虫找信使萤火虫，即找树的叶子节点，此时时间复杂度为O（N）。假设叶子节点数量为L，则完成融合矩阵merge_array的所有更新，耗时O（L×k），其中k为每个叶子节点对应的近邻。因此，聚萤成树模块的时间复杂度为O（max（N，L×k））。

整体来看，算法主要由腐草生萤、萤翅流光、聚萤成树这三大模块构成。

腐草生萤模块确定了每只萤火虫的亮度和自适应近邻数并且完成了初步聚类，该模块的时间复杂度为O（max（K×N×log（N），N×max_k）），其中K为数据集维度，N为数据集大小，max_k为最大限制近邻数。

聚萤成树模块通过同频树对初步聚类的簇进行合并，实现最终聚类，该模块的时间复杂度为O（max（N，L×k）），其中N为数据集大小，L为叶子节点数目，k为每个叶子节点对应的近邻数。

由于O（max（K×N×log（N），N×max_k））>O（max（N，L×k）），该算法的时间复杂度为O（max（K×N×log（N）， N×max_k））。考虑到max_k的设置一般小于K×log（N），因此算法的时间复杂度可以近似为O（K×N×log（N）），在聚类算法中属于较低的时间复杂度，对大规模数据集友好，具有较快的运行速度。

2 实验

本章进行了大量实验，从准确度、完整度等多角度综合评价FLINCA算法的聚类结果。具体而言，FLINCA在4个二维数据集和3个多维真实世界数据集上与12种不同的算法进行了对比实验，通过8种不同的评价指标从多角度衡量了模型的聚类效果。

2.1 指标分析及实现环境

2.1.1 对比算法、数据集、评价指标介绍

为了验证算法的性能，实验与12种著名的聚类算法进行了比较，相关参数设置在表1、2中，有关FLINCA的参数设定在实验结果对应的表头中。在评价指标上，本文采用Rand index（RI）［26］、adjusted Rand index（ARI）［27］、adjusted mutual information（AMI）［28，29］、normalized mutual information（NMI）［28，29］、homogeneity score（HS）［30］、completeness score（CS）［30］、V measure score（VMS）［30］、Fowlkes Mallows index（FMI）［31］作为评价指标。RI可以测量预测标签与真实标签的相似度。ARI和RI类似，但是它可以等于0。NMI和AMI类似，但它采用了不同的归一化方法。HS指标用于衡量聚类的纯粹度，如果一个预测簇里只包含了一种真实簇的点，那么说明这个簇的聚类结果纯粹。CS用于衡量一个聚类结果的完整性，如果真实簇的点没被聚到不同的预测簇里，那么说明聚类完整。VMS是结合了HS和CS的综合评价指标。FMI是准确率和召回率的综合评价。

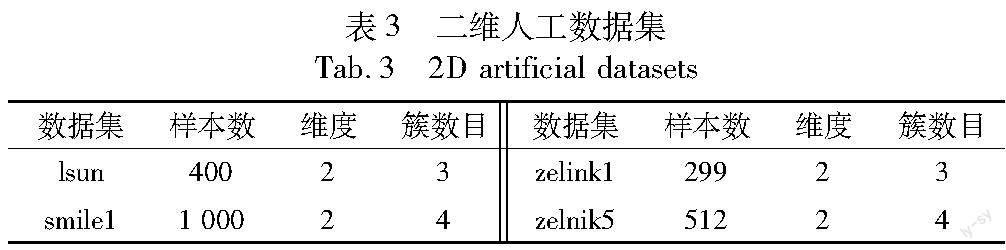
本实验所使用的数据集被分为两部分，分别是二维人工数据集和真实世界数据集，它们都被用于检验算法。具体而言，本文使用了4个二维人工数据集，如表3所示，这些数据集中的数据显示不同的分布。此外，为了证明算法能够处理真实世界聚类任务的各种挑战，算法在3个真实数据集进行验证，这些数据集的描述如表4所示。为了衡量算法对这7个数据集的效果，实验采用了8种不同的评价指标如表5所示，以此从不同的角度尽可能客观地衡量算法的效果。

2.1.2 实验环境

进行实验的硬件环境为处理器Intel CoreTM i7-8650U CPU@1.90 GHz 2.11 GHz、内存8.00 GB，进行实验的软件环境为操作系统Windows 11、PyCharm 2021、Python 3.8，实验进行前所有数据均已进行标准化处理。

2.2 人工数据集

在二维的數据集中，FLINCA与其他12种聚类算法在8种不同的评价指标下进行了实验，为了更直观地展现聚类结果，实验还对二维数据集的聚类结果进行了可视化，生成了对应的二维聚类效果图，如图3、4所示。

图3、4展示了FLINCA在4个二维数据集上的平均聚类结果。从中可以看出，FLNICA在各项指标中都取得了最好的成绩和完美的聚类效果，因此它所对应的所有指标得分均为1.000 000。这源于FLINCA具有依靠亮度捕捉数据信息、自适应近邻数、无须指定具体簇数目等特性。

从图3可以看出，FLINCA的聚类结果优于同类型的基于萤火虫的仿生学聚类算法。具体而言，由于IIEFA是基于萤火虫算法对K-means算法进行了优化，所以仍可能存在K-means算法相应的问题，如“簇割裂”现象。比如在lsun数据集中，带状分布的长条形数据容易因为离非归属簇的簇中心更近，从而被分配到错误的簇。同样地，在smile1数据集中，脸颊部分的数据点容易被眼睛、嘴巴等密度更高的区域形成的局部簇中心影响，从而被分配到错误的簇。此外，对于FFC算法而言，由于其通过模糊函数进行聚类，所以算法具有一定的随机性，从而容易出现簇混杂现象。比如在zelnik1数据集中，最外层环被聚类成了多个小环，每个小环内混杂了归属于其他簇的点，而且混杂的点不像IIEFA算法聚类结果那样连续出现，而是间断性出现。对于带状数据集如zelnik5而言，混杂点容易出现在同一个长条内。FA也有类似的问题，且由于该算法需要进行训练，图片仅展示了测试集的聚类效果，但仍可从中看出，其出现了簇割裂和簇混杂现象，这两种情况都会导致簇被污染，从而严重影响聚类结果。

对于FLINCA而言，由于采用了萤翅流光的方法进行初步聚类，避免了像IIEFA那样出现簇割裂现象，同时算法稳定，也不会出现随机结果，从根本上解决了FFC算法中出现的簇污染问题。萤翅流光方法既能迅速完成初步聚类，又能伴随生成同频树，从而有助于簇融合，因此即使初步聚类结果出现聚类结果不完整的现象，也能依靠聚萤成树完成最终的簇分配。

从图4可以看出，FLINCA也优于传统聚类算法，相较于基于密度的聚类算法如DBSCAN、FLINCA，能更好地处理环状数据集。以数据集lsun为例，从图4可以看出，基于密度的DBSCAN和OPTICS算法同样有较好的表现，FLINCA算法中的亮度概念和密度近似，同样能很好地捕捉数据集中的密度关系。此外，FLINCA在zelnik1数据集上的聚类效果也很好，其原因是FLINCA采用自适应的方式动态估计每个点的近邻数，这样能够更好地捕捉数据集的密度特征，而不是像DBSCAN那样需要固定近邻范围。

此外，从图4可以看出，基于密度的算法在对环状数据集进行聚类时，容易出现断裂的现象，这主要是因为数据空间中密度分布并不均匀，如果设置固定的近邻数，容易丢失全局信息。然而，FLINCA采用最大似然估计的方式来获得自适应近邻数，可以很好地解决这一问题，因此FLINCA可以很好地捕捉环状数据集的特征。此外，在解决簇断裂问题上，FLINCA采用了聚萤成树的方式，这种方式效果比较稳定，使得FLINCA在8种指标的评价下都取得了最佳成绩，在图4中取得了完美的聚类效果。

相较于基于层次的聚类算法，如BIRCH和agglomerative clustering算法，有更多元的方式去衡量点与点之间的关系，且在进行簇合并时并不是简单地依赖距离，而是依赖同频树的信息，因此聚类效果更优秀。

相较于基于信息传递的聚类算法，如affinity propagation算法，FLINCA不仅效果更好，而且运行速度更快。affinity propagation需要迭代T轮，每轮需要更新点与点之间的关系，最坏情况的时间复杂度为O（T×N2），其中T为迭代次数，N为数据集大小。相比之下，FLINCA的时间复杂度仅为O（K×N×log（N）），其中K为数据集维度，N为数据集大小。

相比于基于分区的聚类算法，如K-means++、FLINCA无须指定具体的簇数目，这样更加符合实际应用，且聚类结果更加稳定。此外，K-means++仅通过欧氏聚类确定簇心并且聚类，这也会导致聚类判断不准确，这种不准确主要体现在条状数据集上如zelnik5，在确定完簇心后如果仅通过欧氏距离进行聚类，那么本属于同一个簇的数据点会被分隔为两个不同的簇，出现条断裂现象。而FLINCA通过亮度完成聚类，不仅考虑了欧氏聚类，还考虑了近邻的影响，因此在zelnik5数据集上，FINLCA能够领先K-means++算法。

2.3 真实数据集

为了探寻FLINCA在实际应用中的效果，将FLINCA应用到真实世界数据集上。从表5可以看出，在所有真实世界数据集的聚类效果对比中，FLINCA在8项平均指标中有7项平均指标占有优势，处于所有对比算法中的第一名。仅在指标上分别落后affinity propagation算法0.016 012。此外，从表6可以看出，FLINCA在所有指标上都优于其他算法。即使DBSCAN算法在CS指标上达到1.000 000，但它的ARI、AMI、NMI、HS、VMS指标均为0.000 000，这意味着DBSCAN算法聚类失败，将所有点聚成同一个簇，属于无效的聚类。因此，可以认为FLINCA在wine数据集上优于其他所有算法。

同样使用了密度这一概念，FLINCA和DBSCAN算法在表6中出现显著差异的原因主要来源于，FLINCA采用了自适应近邻的方式来更好地捕捉数据集的密度特征。此外，考虑到wine数据集维度较高，IIEFA并不太适用于该数据集，通过萤火虫的迭代对簇心算法进行更新会受限于高维度下的欧氏距离，因此不能很准确度地捕捉数据间的特征，聚类效果较差。同为萤火虫聚类算法的FFC算法因为适用于高维数据，所以算法效果较为出色。此外，FA的效果也较好，但该算法需要数据集提供标签进行训练，成本较高，因此其应用范围受一定限制。相比之下，FLINCA具有出色的聚类结果，且不需要进行训练，这也验证了它能很好地捕捉高维数据集的数据分布特征。

从表7可以看出，在数据集zoo中，FLINCA在8项平均指标中有7项平均指标占有优势，处于所有对比算法中的第一名。僅在HS指标上分别落后affinity propagation算法0.108 725。affinity propagation算法在HS指标上的得分更高，这说明affinity propagation算法的聚类结果更纯粹，它预测的聚类簇可能会比较小，但是能保证每个小簇的聚类结果都尽量准确，让小簇尽量准确也是FLINCA的一个优化方向。目前FLINCA可以通过让自适应近邻数变小，从而获得更多准确的小簇，之后再通过簇融合将小簇合并为大簇，但随着自适应近邻数的缩小，对于最大似然估计的结果也可能变得更不准确，针对小簇的优化也是模型的缺陷之一，后续的研究将根据这点进行优化和完善。

这种缺陷在小近邻簇上会暴露得比较明显，以iris数据集为例，从表8可以看出，FLINCA在所有指标中没有一项处于最优的位置，基本上处于第3或第4。这是因为iris数据集的特殊性，其密度最高点对应的最大近邻数较小，而边缘点对应的最大近邻数较多，数据分布较为分散。虽然FLINCA仍然超过了大部分的对比算法，特别是领先于同是基于仿生学的ACOC和LF算法。具体而言，FLINCA在各指标上分别领先ACOC算法0.164 071 266、0.676 326 929、0.726 076 008、0.614 684 296、0.589 646 857、0.638 979 268、0.614 684 296、0.604 405 179。由于ACOC算法需要通过蚁群实现信息素叠加完成聚类，所以需要进行多轮迭代。如果迭代次数不足，则无法达到令人满意的聚类效果，这种信息素迭代也会消耗大量计算资源。而FLINCA只需执行一次便能获得聚类结果，无须信息素的迭代，而是将生物信息通过频率进行传播，将信息交流用于簇合并，因此能够获得更为准确的聚类结果。此外，FLINCA在各指标上，领先LF算法0.243 371 266、0.680 548 929、0.735 570 0008、0.616 672 296、0.603 252 857、0.627 641 268、0.616 672 296、0.536 260 179，这是因为LF需要通过蚁群搬运数据点，所以会改变数据空间的密度分布，这也容易导致聚类结果难以收敛，效果不佳。FLINCA不会改变原数据空间的位置分布，因此能领先LF算法。

整体而言，FLINCA具有广泛的应用价值，不仅能够适用于高斯分布的数据集，也能适用于特殊分布的数据集，如环状数据集、条状数据集。此外，在实际应用中，FLINCA能够很好地应对高维数据集带来的挑战，通过亮度传播和簇融合使得聚类结果更加准确。但模型仍存在缺陷——不能很好地处理小近邻簇，这种缺陷主要源于小近邻簇对应的小近邻数与密度的最大似然估计值之间的矛盾。具体而言，近邻数越小，最大似然估计得出的密度值误差越大，这会影响算法的聚类效果，使得聚类不稳定，因此这也是后续的优化研究方向之一。不过综合来看，FLINCA还是能在多种分布、多种维度的数据集上取得较好的聚类效果，且算法时间复杂度低，具有广泛的实际应用价值。

3 结束语

本文提出了一种基于仿生学的萤火虫聚类算法——萤光信息导航聚类算法FLINCA。该算法主要基于两种仿生学思想：一是萤火虫可以通过亮度进行光传播，亮度高的萤火虫会引导亮度低的萤火虫发出同频率的光;二是萤火虫族群之间可以进行信息交流，完成族群融合。这两种思想在聚类算法中便对应着，亮度高的点可以把亮度低的点引导到与自己相同的簇；簇与簇之间可以靠一些特殊的点完成融合。这两种思想诞生出三种萤火虫，根据这三种萤火虫的特性，算法分为三大模块：腐草生萤——产生萤火虫；萤翅流光——引领萤火虫将自己的光传播给其他萤火虫，使得其他萤火虫发出同频率光芒，完成初步聚类；聚萤成树——通过信使萤火虫完成簇融合，实现最终聚类。算法的亮点是采用自适应的方式决定每个点的近邻数；聚类不需要提前指定簇数目；算法运行效率高，时间复杂度仅为O（K×N×log（N）），其中K为数据集维度，N为数据集大小。

为了验证FLINCA的效果，在7种不同分布、不同规模的数据集上进行了多轮实验，其中包括在4个二维数据集和3个多维真实世界数据集上进行实验。为了更准确客观地验证模型，本文采用了8种不同的评价指标从多角度衡量了模型聚类效果。实验表明，FLINCA在这些数据集的大多指标上，优于12种不同的对比算法。因此，可以认为FLINCA表现出色，适用于多种情况，具有广泛的应用价值。

参考文献：

[1]常黎明，刘颜红，徐恕贞.基于数据分布的聚类联邦学习［J］.计算机应用研究，2023，40（6）：1697-1701.（Chang Liming， Liu Yanhong， Xu Shuzhen. Clustering federated learning based on data distribution［J］.Applications Research of Computers，2023，40（6）：1697-1701.）

［2]Taha K. Semi-supervised and un-supervised clustering： a review and experimental evaluation［J］.Information Systems，2023，114：102178.

［3]Xie Yiqun， Shekhar S， Li Yan. Statistically-robust clustering techniques for mapping spatial hotspots：a survey［J］.ACM Computing Surveys，2022，55（2）：1-38.

［4]Zhakubayev A， Hamerly G. Clustering faster and better with projected data［C］//Proc of the 6th International Conference on Information System and Data Mining.2022：1-6.

［5]郑璐依，黄瑞章，任丽娜，等.关键语义信息补足的深度文本聚类算法［J］.计算机应用研究，2023，40（6）：1653-1659.（Zheng Luyi， Huang Ruizhang， Ren Lina， et al. Deep document clustering method via key semantic information complementation［J］.Applications Research of Computer，2023，40（6）：1653-1659.）

［6]Zeng Shijie， Wang Yuefei， Yang Yixi. A novel prognosis model based on comprehensive analysis of pyroptosis-related genes in breast cancer［EB/OL］.（2022-04-05）.［2023-06-28］.https：//doi.org/10.1101/2022.04.05.486932.

［7]Militello C， Rundo L， Dimarco M， et al. Semi-automated and interactive segmentation of contrast-enhancing masses on breast DCE-MRI using spatial fuzzy clustering［J］.Biomedical Signal Processing and Control，2022，71：103113.

［8]Niu Xinzheng， Zheng Yunhong， Liu Wuji， et al. On a two-stage progressive clustering algorithm with graph-augmented density peak clustering［J］.Engineering Applications of Artificial Intelligence，2022，108：104566.

［9]Facco E， dErrico M， Rodriguez A， et al. Estimating the intrinsic dimension of datasets by a minimal neighborhood information［J］.Scientific Reports，2017，7（1）：12140.

［10]Rodriguez A， dErrico M， Facco E， et al. Computing the free energy without collective variables［J］.Journal of Chemical Theory and Computation，2018，14（3）：1206-1215.

［11]王躍飞，于炯，苏国平，等.ODIC-DBSCAN：一种新的簇内孤立点分析算法［J］.自动化学报，2019，45（11）：2107-2127.（Wang Yuefei， Yu Jiong， Su Guoping， et al. ODIC-DBSCAN：a new analytical algorithm for inliers［J］.Acta Automatica Sinica，2019，45（11）：2107-2127.）

［12]Frey B J， Dueck D. Clustering by passing messages between data points［J］.Science，2007，315（5814）：972-976.

［13]Vassilvitskii S， Arthur D. K-means+：the advantages of careful seeding［C］//Proc of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms.2006：1027-1035.

［14]Sculley D. Web-scale K-means clustering［C］//Proc of the 19th International Conference on World Wide Web.2010：1177-1178.

［15]Murtagh F， Legendre P. Wards hierarchical agglomerative clustering method：which algorithms implement Wards criterion？［J］.Journal of Classification，2014，31（3）：274-295.

［16]Zhang T， Ramakrishnan R， Livny M. BIRCH：an efficient data clustering method for very large databases［J］.ACM SIGMOD Record，1996，25（2）：103-114.

［17]Ester M， Kriegel H P， Sander J， et al. A density-based algorithm for discovering clusters in large spatial databases with noise［C］//Proc of the 2nd International Conference on Knowledge Discovery and Data Mining.1996：226-231.

［18]Ankerst M， Breunig M M， Kriegel H P， et al. OPTICS： ordering points to identify the clustering structure［J］.ACM SIGMOD Record，1999，28（2）：49-60.

［19]Bharti V， Biswas B， Shukla K K. A novel multiobjective GDWCN-PSO algorithm and its application to medical data security［J］.ACM Trans on Internet Technology，2021，21（2）：1-28.

［20]Shelokar P S， Jayaraman V K， Kulkarni B D. An ant colony approach for clustering［J］.Analytica Chimica Acta，2004，509（2）：187-195.

［21]Lumer E D， Faieta B. Diversity and adaptation in populations of clustering ants［C］//Proc of the 3rd International Conference on Simulation of Adaptive Behavior：from Animals to Animats 3.1994：501-508.

［22]Yang Xinshe. Nature-inspired metaheuristic algorithms［M］.［S.l.］：Luniver Press，2010：81-89.

［23]Senthilnath J， Omkar S N， Mani V. Clustering using firefly algorithm：performance study［J］.Swarm and Evolutionary Computation，2011，1（3）：164-171.

［24]Xie Hailun， Zhang Li， Lim C P， et al. Improving K-means clustering with enhanced firefly algorithms［J］.Applied Soft Computing，2019，84：105763.

［25]Banu P K N， Azar A T， Inbarani H H. Fuzzy firefly clustering for tumour and cancer analysis［J］.International Journal of Modelling， Identification and Control，2017，27（2）：92-103.

［26]Hubert L， Arabie P. Comparing partitions［J］.Journal of Classification，1985，2（1）：193-218.

［27]Steinley D. Properties of the Hubert-Arable adjusted rand index［J］.Psychological Methods，2004，9（3）：386.

［28]Vinh N X， Epps J， Bailey J. Information theoretic measures for clusterings comparison： variants， properties， normalization and correction for chance［J］.The Journal of Machine Learning Research，2010，11：2837-2854.

［29]Strehl A， Ghosh J. Cluster ensembles：a knowledge reuse framework for combining multiple partitions［J］.Journal of Machine Learning Research，2002，3（12）：583-617.

［30]Rosenberg A， Hirschberg J. V-measure：a conditional entropy-based external cluster evaluation measure［C］//Proc of Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning.2007：410-420.

［31]Fowlkes E B， Mallows C L. A method for comparing two hierarchical clusterings［J］.Journal of the American Statistical Association，1983，78（383）：553-569.