基于子空间学习的快速自适应局部比值和判别分析

曹传杰 王靖 赵伟豪 周科艺 杨晓君

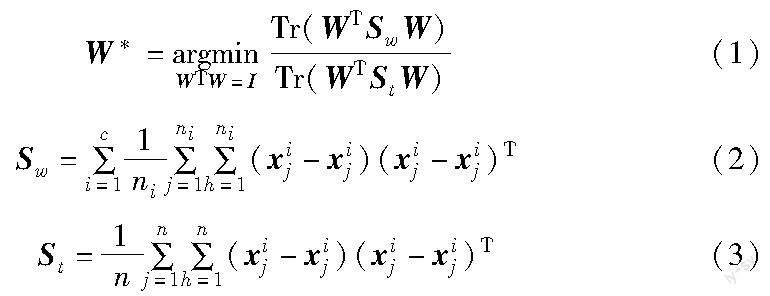
摘 要：降维是处理高维数据的一项关键技术，其中线性判别分析及其变体算法均为有效的监督算法。然而大多数判别分析算法存在以下缺点：a）无法选择更具判别性的特征；b）忽略原始空间中噪声和冗余特征的干扰；c）更新邻接图的计算复杂度高。为了克服以上缺点，提出了基于子空间学习的快速自适应局部比值和判别分析算法。首先，提出了统一比值和准则及子空间学习的模型，以在子空间中探索数据的潜在结构，选择出更具判别信息的特征，避免受原始空间中噪声的影响；其次，采用基于锚点的策略构造邻接图来表征数据的局部结构，加速邻接图学习；然后，引入香农熵正则化，以避免平凡解；最后，在多个数据集上进行了对比实验，验证了算法的有效性。

关键词：降维； 线性判别分析； 子空间学习； 比值和

中图分类号：TP391.4   文献标志码：A   文章编号：1001-3695（2024）01-017-0108-08

doi：10.19734/j.issn.1001-3695.2023.05.0194

Fast adaptive local ratio sum discriminant analysis based on subspace learning

Abstract：Dimensionality reduction is a key technique for processing high-dimensional data， and linear discriminant analysis and its variant algorithms are effective supervised algorithms. However， most discriminant analysis algorithms have the following disadvantages： a）It cannot select more discriminative features; b）It ignores the interference of noise and redundant features in the original space; c）The computational complexity of updating the adjacency graph is high. In order to overcome these shortcomings， this paper proposed a fast adaptive local ratio sum discriminant analysis algorithm based on subspace learning. Firstly， this paper proposed a model that unified the ratio sum criterion and subspace learning to explore the potential structure of the data in the subspace， select features with more discriminative information， and avoid being affected by noise in the original space. Secondly， it used an anchor-based strategies to construct an adjacency graph to represent the local structure of the data to accelerate the learning of the adjacency graph. Finally， it introduced Shannon entropy to avoid trivial solutions， and verified the effectiveness of the algorithm by comparison experiments on multiple data sets.

Key words：dimensionality reduction; linear discriminant analysis; subspace learning; ratio sum

0 引言

在如今传感器技术快速发展的背景下，采集的数据维度也随之快速增长，涌现出越来越多的高维数据［1］，然而維度的增加导致了计算复杂度剧烈增加，以及原始数据中存在大量冗余特征等问题［2］，阻碍了一些领域的发展，如视频分析［3］、人群分析［4］、图像分析［5］等。因此，设计一个用来提取数据的内在结构，以寻求数据最优表示的降维算法是极其紧迫的。

在过去的几十年，大量学者提出了许多的特征提取方法。其中主成分分析（principal component analysis，PCA）［6］和线性判别分析（linear discriminant analysis，LDA）［7］分别是无监督和有监督领域最著名的特征提取算法。LDA通过寻找一个投影矩阵，将高维数据投影于低维空间中，以寻求使得类内散度最小和类间散度最大的低维表示。LDA可归纳为求解迹比（trace ratio，TR）［8］问题，然而TR问题不能直接获得全局最优的封闭解［9］，通常需要转换为迹差问题，通过广义特征值求解得到近似解，这会影响后续分类的性能。此外，LDA还存在小样本量、最大维度限制等缺点。因此，近年来，许多研究工作采用正交线性判别分析［10］、最大裕度准则［11］来解决上述问题。

上述算法皆只适用于服从高斯分布的数据，而无法处理更为复杂分布的真实世界数据。为了解决这一问题，受到局部投影保持［12］的启发，局部费舍判别分析（local Fisher discriminant analysis，LFDA）［13］通过引入样本之间的相似度来构造局部散度矩阵，以代替全局散度矩阵，能更好地提取数据的局部信息。此外，Cai等人［14］提出了一种局部感知判别分析（locality sensitive discriminant analysis，LSDA），该算法通过引入KNN思想，使样本的感受野只在近邻样本内，利用近邻关系构造类内图和类间图，以使得每个局部区域最大化不同标签近邻点的彼此距离，最小化相同标签的近邻点彼此距离。有学者注意到，根据TR准则来进行特征提取，会倾向于选择投影方向上总体方差较小或趋于零的方向，而这些不具有强烈判别性的特征对于分类任务是无意义的。为此，有学者提出了比值和（ratio sum，RS）［15］准则来避免这个问题，该准则会更倾向于选择总体方差较大的组合。这种准则已经在许多文章中被证明是有效的，例如，贪心比值和（greedy ratio sum，GRS）［15］与比值和线性判别分析（ratio sum linear discriminant analysis，RSLDA）［16］。

此外，张家乐等人［8］注意到基于图嵌入降維算法的缺点，即它们在原始空间中学习忽略了噪声和冗余特征的干扰，且构图方式受到调参的影响，这使得构图不合理，导致性能下降。为此，张家乐等人提出了自适应近邻局部比值和线性判别分析算法（adaptive neighbor local ratio sum linear discriminant analysis，ANLRSLDA），通过采用非热核自适应构图策略构建邻接图，能在一定程度上减少原始空间中噪声和冗余特征带来的影响。但该算法仍然是基于原始空间进行构图，因此，无法避免原始空间中噪声和冗余特征的影响。文献［17］认为数据的内在几何形状隐藏在低维空间中，因此，每个样本的邻域应在子空间中寻找，而不是在原始空间中。为此，大量研究者付出巨大努力。例如，自适应局部线性判别分析（adaptive local linear discriminant analysis，ALLDA）［18］和动态最大熵图（dynamic maximum entropy graph，DMEG）［19］等方法通过迭代算法，自适应地学习子空间中数据的局部关系，以避免原始空间中噪声的影响。但上述子空间学习算法是根据全部数据点之间的相似度或重构关系来学习局部信息，导致更新邻接图的时间复杂度至少是样本数量的平方，这意味着此类算法训练大规模的数据集是非常耗时的。为了更准确、更具鲁棒性、快速地学习局部流形结构，本文提出了一种快速自适应比值和局部判别分析（fast adaptive local ratio sum discriminant analysis，FALRSDA）算法。该算法能很好地学习更具判别性的特征和数据潜在局部结构，同时能快速地自适应学习最优的子空间邻接图。

本文的主要贡献为：a）建立了一种快速、自适应的比值和分析判别模型，统一了投影矩阵、内在流形结构和类内划分的学习，以学习更具判别性的特征和探索低维的潜在结构，并提出了一种高效的迭代优化算法来求解该模型;b）基于锚点［20］的策略加速构造邻接图，降低了算法的时间复杂度;c）邻接图会自适应学习，可消除原始空间的噪声干扰，并且引入最大熵控制图权值的均匀性，避免平凡解。同时，锚点的自适应分配可隐式地将每个类划分为不相交的簇，以探索数据的局部结构，使算法适用于同类非高斯分布的数据。

1 相关工作

1.1 线性判别分析

设数据矩阵X=［x1，x2，…，xn］∈RApd×n，其中n为样本数，xi∈RApd×1是单个样本，具有d个特征维度。假设数据X已经按标签大小排序。LDA的目标是寻找一个最优投影矩阵W=［w1，w2，…，wk］∈RApd×k，其中d>>k，k为降维的维数，通过Y=WTX∈RApk×n将数据映射到低维空间中，使得同类数据变近，而不同类数据更远。LDA具有许多变种［19］，LDA的目标函数之一可以写成以下TR问题：

其中：Sw为类内散度矩阵;St为总体方差矩阵;c是样本类数;ni是第i类样本个数;n是样本总数。最优的投影矩阵W*可通过求解式（1）得到。

1.2 比值和线性判别分析

式（1）也可被写为

然而LDA采用TR准则会导致最优投影矩阵倾向于选择方差较小的投影方向，使得降维后的数据在个别投影方向上的方差很小，因此所选择的子空间低维特征的判别性较低［16］。对于分类任务，没有强烈判别性的特征对于分类任务的影响是极低的，但数据存储却需要更多空间。显然，选择方差较小的投影方向不利于分类问题。幸运的是，文献［15］提出了新的RS准则，并证明了RS准则可以避免TR更倾向于选择方差较小的投影方向的缺点。用RS准则替换TR准则，可得到模型：

下面给出一个简单例子，来比较TR和RS准则在LDA中选择投影方向的区别，以证明RS在LDA中的优势。如表1所示，假设有三个相互独立的投影方向，其类内距离为wTpSwwp，总体方差为wTpStwp，假设需要保留两个投影方向，则TR准则的数值关系如下：

对于TR准则，根据式（4），会倾向于选择投影方向1和投影方向3。而RS准则的数值关系如下：

同样，根据式（5），投影方向1和2会被RS准则选择出来。根据TR准则选择出来投影方向1和3的组合，因投影方向3方差较小，使得该组合的整体判别性较小，相比之下，RS会选择出方差大的投影方向1、2组合，显然，RS选择的组合更具判别性。由此可以看出，RS可以避免选择方差较小的投影方向，以提高降维后低维数据的判别性。

2 快速自适应局部比值和判别分析算法

2.1 局部比值和线性判别分析模型

虽然比值和模型可以选择更具判别性的特征，但模型只关注样本的全局信息，这导致模型只适用于服从高斯分布的数据集，使得算法的应用十分受限。而在现实世界中，数据集往往是服从非高斯分布的，如流形数据。受到LFDA的启发，数据的局部结构能更适合流形数据的嵌入［13］，因此将样本的局部信息引入到式（5）的模型中。为了更好地阐述模型的物理意义，先将式（5）展开为向量对形式，具体如下：

其中：Si的第h行第h列元素为sijh、sijh为第i类的第j个样本和第h个样本的相似度，相似度越大，表示两样本距离越近、越相似。传统计算sijh通过高斯核函数得到，如下所示。

sijh=exp（－（‖xij－xih‖22/σ））（10）

其中：σ为任意正数。与式（8）相比，式（8）是式（9）的Si的每个元素都为1/ni的情况，即同类样本之间的权重相同，这意味模型会优先优化彼此距离远的样本，而不关注与彼此较近的样本关系，从而无法保留样本的局部结构。对于式（9），为了目标函数最小化，式（9）会更关注sijh大的两个样本，即更关注局部较近的样本信息，从而保留局部结构。

2.2 基于香农熵的自适应子空间学习

雖然在2.1节提出了局部比值和模型，但相似度的获取是从原始空间中的样本得到，一旦原始空间受到了噪声和冗余特征的污染，会直接影响相似度的评判，且式（10）获取的sijh是否合理，依赖σ的选取，这些缺点将极大地影响算法的性能。

本文认为最优邻接图应在最优化子空间中寻找，这是由于降维的实质是寻找数据的低维嵌入结构，而最优邻接图理应由低维嵌入结构得到。因此，邻接图应由在子空间中的低维数据WTX得到，而不应如式（10）的方式，由原始空间数据而得到。根据子空间来学习邻接图，可避免直接受到原始空间噪声和冗余特征的干扰。具体来说，算法会交替优化投影矩阵W和相似度矩阵S，利用子空间的数据学习S，且交替时无须调参，可以自适应学习邻接图，以更好地表征样本的局部结构。

但对式（9）优化S时，极易陷入平凡解，举个简单的例子，假设sij为第i类相似度矩阵Si的第j行，sij只有三个元素。显然sij的最优解为设置离第j个样本最近的样本权重为1，其他权重为0，即可使目标函数最小的值，如sij为［1，0，0］，但这是平凡解，因为只能保留最近样本的局部信息。而理想的最优解应能保留多个近邻点的局部信息。因此，引入香农熵H（sij）=-∑nih=1sijhln sijh。-H（sij）作为惩罚项，在出现解［1，0，0］时，值最大，以惩罚目标函数，使sij考虑元素权值分配更均匀的解。式（9）重写为

其中：γ是平衡因子，用于权衡判别分析和香农熵之间的关系。

2.3 基于锚点的加速策略

2.2节提到了子空间学习需要迭代更新S，但更新S的时间复杂度至少为O（n2），对大数据集而言，这个时间复杂度是难于令人接受的。针对子空间学习这一缺点，本文采用锚点的策略，通过锚点和样本之间的相似度来表征低维数据的局部结构，以实现更新S的加速，式（11）重写为

3 算法优化

优化式（12）是一个NP问题，为了高效优化该问题，采用交替迭代的策略：固定W、S，更新U；固定U、S，更新W；固定U、W，更新S。

1）固定W和S，优化锚点矩阵U

由于固定S和W，则式（12）中的香农熵项和分母项为常数，所以，优化问题可简化为

若忽略较小sijh，锚点物理含义表现为周围同类点的中心，隐式地将同类数据划分为不同的簇，使同簇样本越近越好，以探索数据局部结构，而不是关注数据的全局结构，使得算法能适应同类非高斯分布的数据。举个简单例子说明利用锚点探索局部结构是有效的，如图1所示，类别1是同类非高斯分布数据，可以明显分为两个簇。根据LDA使同类数据越近越好的思想，在全局视角下，不难想象图1在全局情况下的投影方向，而投影结果是类别1和2的数据混在一起，难以区分；而在局部视角下，类别1的锚点会把周围相似度高的同类样本划分为不同簇，对于优化来说，不同簇可以被认为是不同的类，因此可得到局部情况下的投影方向，在投影后，依然保持对两类别的区分度，说明了局部算法可以适用于同类非高斯分布的数据。

根据式（15）便可依此类推，随着锚点的自适应更新，得到最优锚点矩阵U。

2）固定U和S，优化投影矩阵W

为方便优化，固定S和U，根据式（15），则式（12）可简化为

对于式（16）的任意第p项，可分为如下两个子问题。

根据式（3），式（17）可简化为

为了简化式（18），提出以下引理1，并详细证明引理1。

式（21）可展开为

显然，式（22）的三项可以用迹函数的形式表达，如下所示。

其中：D1、D2为对角矩阵，D1的第j个对角元素为∑vih=1sijh，D2的第h个对角元素为∑nij=1sijh。由约束∑vih=1sijh=1和式（23）可得

由式（15）转为矩阵形式，可得i=XiSiDi，代入式（24）（25）得

结合式（26）～（28），式（21）可重写为

因此，由式（18）可得

证毕。由引理1，且令SL=XLXT，式（16）可简化为

为了优化式（31），不妨假设投影矩阵中只有一项wp，而其他的投影方向已达到最优。由于求解wp应取决于投影方向，而不是wp的模长，所以可以进行放缩，则式（31）可转换为

其中：W（p）=［w1，wp-1，wp+1，…，wk］T，0为全0向量。构造式（32）的拉格朗日函数为

L（Wp，α，λ）=wTpStwp-αTWT（p）wp，λ（wTpSLwp-1）（33）

其中：α=［α1，α2，…，αk－1］T和λ皆为拉格朗日乘子。对式（33）关于wp求导，并令式（34）为0。

令μ=1/（2α），对上式左乘WT（p）S－1L得

μ=（WT（p）S－1LW（p））－1WT（p）S－1LStwp（35）

将式（35）代入式（34），可得

（I-S－1LW（WT（p）S－1LW（p））－1WT（p））S－1LStwp=λwp（36）

对上式左乘wTpSL，且wTpW（p）=0，可得

因此，式（32）的解wp为式（38）特征值分解的最大特征值所对应的特征向量。

（I-S－1LW（WT（p）S－1LW（p））－1WT（p））S－1LSt（38）

依此类推，便可迭代优化出投影矩阵W的k列向量。

3）固定U和W，优化相似度矩阵S

由于固定U和W，则式（12）可被改写为

注意到，对式（39）的每个类的优化问题是相互独立的，并且对于Si的每一行也可单独求解。因此，对Si的第j行sij的优化可以表述为以下问题：

其中：η是拉格朗日算子。对式（41）关于sijh求导，且令求导结果为0，如下所示。

则有

结合约束∑vih=1sijh=1和式（44），则有

将式（44）代入式（43），可得

可以注意到，式（45）总是满足约束0≤sijh≤1。因此，通过式（45）即可计算出最优的相似度矩阵S。综上，利用式（15）（38）和（45）交替优化锚点矩阵U、投影矩阵W和相似度矩阵S，直到式（12）的目标函数值收敛，即可得到最优的W。

3.1 FALRSDA算法流程

算法1 FALRSDA

输入：原始数据X，标签矩阵Y，每类的锚点个数vi，正则化系数γ。

输出：投影矩阵W。

a）初始化：对原始数据X按标签进行排序，且进行归一化处理。随机初始化满足WTW=I的投影矩阵W。通过模糊聚类算法得到第i类相似度矩阵Si。

b）根据式（20），更新L。

c）根据式（38），更新每个wp。

d）根据式（15），更新每个Ui。

e）根据式（45），更新每个Si。

f）重复步骤b）～e），直到收敛。

3.2 时间复杂度分析

本文算法输入的训练矩阵为X∈RApd×n，d为维数，n为样本数，降维维数为k。为了方便，假设每个类的锚点数是相同的v。时间复杂度主要由迭代更新投影矩阵W、相似度矩阵S和更新锚点U来提供，迭代收敛需要的次数为t，则更新投影矩阵W所需的时间复杂度为O（k（d3+d2k+dk2+k3）），更新相似度矩阵S所需的时间复杂度为O（nkd+cvdk+nkv+nvlog（v）），锚点矩阵U所需的时间复杂度为O（cvdk）。考虑到n>>c、n>>v和d>>k，因此，FALRSDA总的时间复杂度可近似为O（t（kd3+nkd）），且对于大数据集n>>d，算法的时间复杂度可近似为O（tnkd）。

4 实验与分析

在本章中，所有实验在MATLAB R2017b，计算机CPU为Intel i5-8500 3.00 GHz，内存为16 GB的实验环境中进行。本文将通过以下实验来验证算法的有效性：a）在合成数据上的二维数据鲁棒可视化实验;b）在8个真实数据集上的分类实验;c）收敛和运行时间实验。

4.1 对比算法和参数设置

为验证本文算法的有效性，将FALRSDA与LDA、GRS、ANLRSLDA、LFDA、LSDA、ALLDA、DMEG等降维算法进行对比实验。其中LDA、GRS是全局降维算法，其余为局部降维算法，特别地，GRS、ANLRSLDA是基于RS准则的降维算法，ALLDA、DMEG是具有子空间学习能力的降维算法。在本次实验中，LDA的降维维数设置为［1：min（d－1，c－1）］，而其余算法的降维维数都设置在［1：d－1］搜索，而LFDA、LSDA、ALLDA、DMEG的类内近邻数［1：o－1］，o是数据集中最小类样本数，单独地，将LSDA类间近邻数设置为10，DMEG的超参数根据文献［19］给出的经验值设置为1，其余超参数皆从［0.001，0.01，0.1，1，10，100］中进行网格搜索，FALRSDA算法的每类锚点数取占本类数［0.1，0.2，0.4，0.6］比率的数量。

4.2 数据集描述及预处理

实验所涉及的数据集共九个，包括一个合成数据集，三个UCI数据集，三个人脸数据集，以及USPS手写数字数据集和Coil20物体数据集。合成数据集由随机高斯函数产生，包含三类，一类为150个样本、两类包含300样本的二维非高斯分布的数据集，如图2所示。UCI数据集包含balance、Australian、German数据集。人脸数据集包括UMIST、YaleB和Pose27。本文实验对所有的数据集进行了归一化处理，为了避免对比算法因样本存在零空间而无法运行，采用PCA对USPS、Coil20和人脸数据集进行预处理，保留样本的95%方差信息，以去除零空间。关于数据集的详细信息如表2所示。

4.3 合成数据集鲁棒性实验

本节在合成数据集上进行了鲁棒性实验，并将结果进行可视化。具体来说，采用高斯随机函数产生两组高维高斯噪声作为合成数据集的扩展维数，其中，两组高斯噪声的维数和方差分别为（15，2）和（250，4）。最后，采用所有的降维算法将这些受噪声污染的数据投影到二维子空间中。结果如图3、4所示。

观察图3、4可以发现，在两种情况中，LDA、GRS总是无法探索其在低维子空间中的内在结构，这主要是由LDA、GRS的全局性导致的，所以无法适用于非高斯分布数据。局部降维算法LFDA、LSDA在两种情况下同样表现不佳，这是因为噪声的维数和方差的增加对原始空间中近邻的选擇有负面影响，说明邻接图容易受到噪声的影响。而ANLRSLDA在噪声较小的情况下，能较好地保存低维数据的局部结构，但在噪声较大时，表现同样不佳。这是由于ANLRSLDA可以自适应构造邻接图，在一定程度上抑制噪声的干扰，但当噪声比较大时，低维数据的局部结构被噪声淹没，而无法提取有效的局部结构。子空间学习算法ALLDA、DMEG、FALRSDA在不同的噪声情况下，都能很好地保留低维数据的局部结构，这表明在最优子空间上学习最优相似图的方式可以有效地避免原始空间中噪声的影响。特别地，根据图4可以看出，FALRSDA相比其他的子空间学习算法具有更好的表现，这归因于自适应的子块分区策略。通过为每个类分配锚点，隐式地划分为多个簇，以此来描述数据的局部结构。此外，本文采用香农熵理论来控制图权值的均匀性，促进了内在结构的学习。

4.4 真实数据集分类实验

在本次实验中，随机选择UCI和人脸数据集的40%的样本作为训练集，60%的样本作为测试集，利用训练集学习出各算法的最优投影矩阵W，再对测试集进行投影。最后采用最近邻分类器对降维后的测试样本进行分类预测，重复10次实验，再统计预测的准确率，以得到平均准确率和方差。在表3中，列出各算法在所有真实数据集中最优的平均准确率和对应的方差以及最优维度，加粗数据表示为同一数据集下的最优结果。图5为在UCI数据集上，不同算法在不同降维数上的准确率曲线。图6（a）为在USPS上的表现，图6（b）（c）为在Coil上各算法的性能表现。图7～9分别为在UMIST、YaleB、Pose27上各算法的性能曲线。

从表3中可以观察到，FALRSDA在所有数据集上的性能表现皆为最好，在Australian能比其他算法都高出3个百分点，在German、USPS数据集都比其他算法高1个百分点，特别地，在balance上，比其他算法高5个百分点。而在Coil20、UMIST数据集上，除了LDA，其他算法都表现得十分优异，特别地，FALRSDA在两数据集上分别达到了99.96%和99.97%的准确率。在YaleB和Pose27数据集上，FALRSDA同樣都比其他算法高0.5～1个百分点。同时在Coil20、UMIST和Pose27数据集上拥有极低的方差。

从图5中可以看出，FALRSDA在balance和German上性能表现始终高于其他对比算法，在Australian上，前面维度FALRSDA表现优秀，但随着维度增加，性能出现下降。在图6（a）中，FALRSDA性能在前面维度与对比算法相差不大，随着维度增加，FALRSDA取得最高的分类准确度。在图6（b）（c）～图9中，FALRSDA在总体上的性能始终高于其他对比算法，但在YaleB和Pose27，随着维度逐渐达到最高，所有算法皆出现了性能下降的现象，这表明当维度达到一定时，增加更多维度并不利于分类任务，反而会增加冗余信息和计算量。与此同时，除了FALRSDA，GRS和ANLRSLDA在所有数据集上的表现同样出色，这归结于RS框架对分类任务的有效性。值得注意的是，LDA在Coil20、UMIST、YaleB上，性能曲线表现最差，但性能曲线依然保持很强的上升趋势，这可能是由最大降维数的限制造成的。

综合上述各种性能表现，说明了FALRSDA算法无论是在低维数据集，还是高维数据集上，都有良好的表现，证明了FALRSDA的有效性。这是由于基于RS准则能够提取更具判别信息的特征，锚点能探索数据的局部结构，子空间学习使其最优的邻接图，所以才有最佳的分类性能表现。

4.5 收敛和运行时间实验

为了验证本文优化算法在寻找最优子空间时目标函数已经收敛，给出在对应3.4节中最优子空间条件下，固定参数γ为1，锚点数量固定为类数的20%，迭代次数为10，8个数据集的目标函数收敛图如图10所示。接着，为了验证本文锚点的加速策略是有效的，在各算法的最优子空间中运行10次，并统计平均值和方差，如表4所示。

对于图10，可以看出本文优化算法在8个数据集上训练，经过10次迭代，所有目标函数皆达到收敛状态，证明了所提出的迭代优化算法的有效性。对于表4，由于子空间学习算法需要迭代更新邻接图，而其他算法无须迭代，所以，非迭代算法在时间上更有竞争力。而本文算法使用的锚点加速策略是针对优化子空间学习算法计算量高的问题，因此可以发现，FALRSDA在所有数据集上花费的时间皆比另外两个子空间学习算法ALLDA和DMEG要少。另外，对于n/d最大的balance数据集，FALRSDA甚至快过非迭代算法ANLRSLDA。因此，证明了本文算法锚点策略的有效性，且在n>>d的条件下，优势更明显。

5 结束语

本文提出了一个基于子空间学习的快速自适应比值和局部判别分析算法。该算法首先采用了比值和准则来避免传统的迹比准则的弊端，以选择更具判别性的投影方向；并且引用保留局部结构的思想和子空间学习，使得算法能探索出样本之间内在的局部结构，同时避免受到原始空间噪声带来的影响；通过引入香农熵约束，使得相似度分布更加均匀，以避免平凡解；针对避免子空间学习计算量大的问题，通过引入锚点，加速子空间学习，同时为同类数据分块，使其适应同类非高斯分布的数据集。最后，通过大量的实验验证了本文算法的有效性。

尽管FALRSDA相较于对比算法有着更好的性能，但笔者认为该算法依然有进一步探索的空间。例如，能否让样本和锚点之间的关系稀疏，而进一步提取低维空间的局部结构和减少噪声的影响，这将是未来探索的方向。

参考文献：

[1]梁露方.Fisher线性判别分析问题的求解算法研究［D］.昆明：云南师范大学，2020.（Liang Lufang. Research on the algorithm of Fisher linear discriminant analysis［D］.Kunming：Yunnan Normal University，2020.）

［2]王继奎，杨正国，刘学文，等.一种基于极大熵的快速无监督线性降维方法［J］.软件学报，2023，34（4）：1779-1795.（Wang Jikui， Yang Zhengguo， Liu Xuewen， et al. Fast unsupervised dimension reduction method based on maximum entropy[J].Journal of Software，2023，34（4）：1779-1795.）

［3]Jia Weikuan， Sun Meili， Lian Jian， et al. Feature dimensionality reduction：a review［J］.Complex & Intelligent Systems，2022，8（3）：2663-2693.

［4]Gao Junyu， Wang Qi， Li Xuelong. PCC Net： perspective crowd coun-ting via spatial convolutional network［J］.IEEE Trans on Circuits and Systems for Video Technology，2019，30（10）：3486-3498.

［5]Wen Jie， Fang Xiaozhao， Cui Jinrong， et al. Robust sparse linear discriminant analysis［J］.IEEE Trans on Circuits and Systems for Video Technology，2018，29（2）：390-403.

［6]Dong Wei， Woz＇niak M， Wu Junsheng， et al. Denoising aggregation of graph neural networks by using principal component analysis［J］.IEEE Trans on Industrial Informatics，2023，19（3）：2385-2394.

［7]Zhu Fa， Gao Junbin， Yang Jian， et al. Neighborhood linear discriminant analysis［J］.Pattern Recognition，2022，123：108422.

［8]張家乐，林浩申，周科艺，等.自适应近邻局部比值和线性判别分析算法［J］.计算机工程与应用，2022，58（22）：291-296.（Zhang Jiale， Lin Haoshen， Zhou Keyi， et al. Adaptive neighbor local ratio sum linear discriminant analysis［J］.Computer Engineering and Applications，2022，58（22）：291-296.）

［9]Guo Yuefei， Li Shijin， Yang Jingyu， et al. A generalized Foley-Sammon transform based on generalized Fisher discriminant criterion and its application to face recognition［J］.Pattern Recognition Letters，2003，24（1-3）：147-158.

［10]Zhao Haifeng， Wang Zheng， Nie Feiping. Orthogonal least squares regression for feature extraction［J］.Neurocomputing，2016，216：200-207.

［11]Luo Fulin， Zhang Liangpei， Du Bo， et al. Dimensionality reduction with enhanced hybrid-graph discriminant learning for hyperspectral image classification［J］.IEEE Trans on Geoscience and Remote Sensing，2020，58（8）：5336-5353.

［12]He Xiaofei， Niyogi P. Locality preserving projections［C］//Proc of the 16th International Conference on Neural Information Processing Systems.Cambridge，MA：MIT Press，2003：153-160.

［13]Sugiyama M. Local Fisher discriminant analysis for supervised dimensionality reduction［C］//Proc of the 23rd International Conference on Machine Learning.New York：ACM Press，2006：905-912.

［14]Cai Deng， He Xiaofei， Zhou Kun， et al. Locality sensitive discriminant analysis［C］//Proc of the 20th International Joint Conference on Artificial Intelligence.San Francisco，CA：Morgan Kaufmann，2007：708-713.

［15]Liang Ke， Yang Xiaojun， Xu Yuxiong， et al. Ratio sum formula for dimensionality reduction［J］.Multimedia Tools and Applications，2020，80（3）：4367-4382.

［16]Wang Jingyu， Wang Hongmei， Nie Feiping， et al. Ratio sum versus sum ratio for linear discriminant analysis［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2021，44（12）：10171-10185.

［17]Luo Tingjin， Hou Chenping， Nie Feiping， et al. Dimension reduction for non-Gaussian data by adaptive discriminative analysis［J］.IEEE Trans on Cybernetics，2018，49（3）：933-946.

［18]Nie Feiping， Wang Zheng， Wang Rong， et al. Adaptive local linear discriminant analysis［J］.ACM Trans on Knowledge Discovery from Data，2020，14（1）：1-19.

［19]Wang Zheng， Nie Feiping， Wang Rong， et al. Local structured feature learning with dynamic maximum entropy graph［J］.Pattern Re-cognition，2021，111：107673.

［20]Wang Rong， Nie Feiping， Yu Weizhong. Fast spectral clustering with anchor graph for large hyperspectral images［J］.IEEE Geoscience and Remote Sensing Letters，2017，14（11）：2003-2007.