一种可实现多运动模态的串并联机构的运动学分析
曾庆山, 马飞凡
(郑州大学 电气与信息工程学院 河南 郑州 450001)
0 引言
随着机器人技术和理论的不断发展,基于串联、并联机器人的工业、商用、军工等发挥着越来越重要的作用。串联机器人具有灵活、工作空间大的特点。并联机器人[1]具有结构稳定、刚度大的特点。随着技术的不断发展,将并联与串联机器人结合而成的混联机构应运而生。混联机构大部分是由少自由度并联机构[2]和串联机构结合而成。
3-RPS是少自由度并联机构中的典型机构,具有两个自由度的转动和一个自由度的移动,这类机构结构简单、易于控制、容易制造且应用很广泛,许多混联机构都采用这类机构作为并联部分本体。自1986年3-RPS机构被Hunt[3]教授提出后,经过长时间的发展改进,目前被广泛应用到机床、零件加工、流水线作业等。Lu等[4]提出了一种求解3-SPR并联机器人位置和工作空间的方法。
串并混联机构兼具串联、并联机构的优点,但其构型复杂,建模难度较高,国内外许多学者对混联机构进行了研究。Lu等[5]提出了由两个3-RPS并联机构串联而成的六自由度混联机构。Lu等[6]采用解析法对文献[5]提出的串并混联机构进行了深入研究。Gallardo等[7]利用螺旋理论研究2(3-RPS)串并结构的奇异位型。李伟等[8]提出了一种串并混联机器人的设计方案,并分析了该机器人的优势及应用场景。机构的位置分析是运动分析、受力分析、动力分析的基础[9]。机构分析中有位置正解和反解两个基本问题。大多数串联机构的正解求解简单,逆解求解复杂。并联机构位置的逆解简单,正解求解复杂,大多数采用封闭解法和数值解法[10]。而串并混联结构的位置分析则更复杂[11]。对于不同的构型,没有较为统一的方法。马春生等[12]提出了一种基于3-SPR的混联机构,分析逆运动学及其机构的工作空间,但没有分析混联机构的正解。李峰等[13]提出了一种针对2(3-RPS)串并联机器人运动构型位置正解的解析算法,该方法复杂且求出的解不唯一。
上述混联机构大多是两层并联机构串联而成,可以实现的功能有限,本文提出了一种新型3-RPS+R+3-SPR混联机构,该机构是由三部分串联而成,可作为爬行机器人的躯干结构,具有多种运动模态,例如转弯、伸缩等。本文对该机构进行了运动学分析,利用并联机构的几何约束求解机构位置逆解,分开求解混联机构的正运动学,便于正运动学的分析,并利用优化算法求解正解的值,避免了求解的不唯一。在Adams中建立机构虚拟样机进行仿真,与Matlab理论计算作对比分析,并给出了具体的数值算例进行正、逆运动学验证。
1 机构构型描述
1.1 机构简介及坐标系建立
为实现多种运动模态,本文提出了一种新型的串并混联机构,其SolidWorks模型如图1所示,机构简图如图2所示。该构型主要由三部分串联构成,下机构为3-RPS,中间为旋转关节,上机构为3-SPR。上、下机构可以伸缩进行蠕动,中间机构可以旋转,上、中、下机构协调运作可以实现蜿蜒。

图1 3-RPS+R+3-SPR模型图Figure 1 The 3-RPS+R+3-SPR model diagram
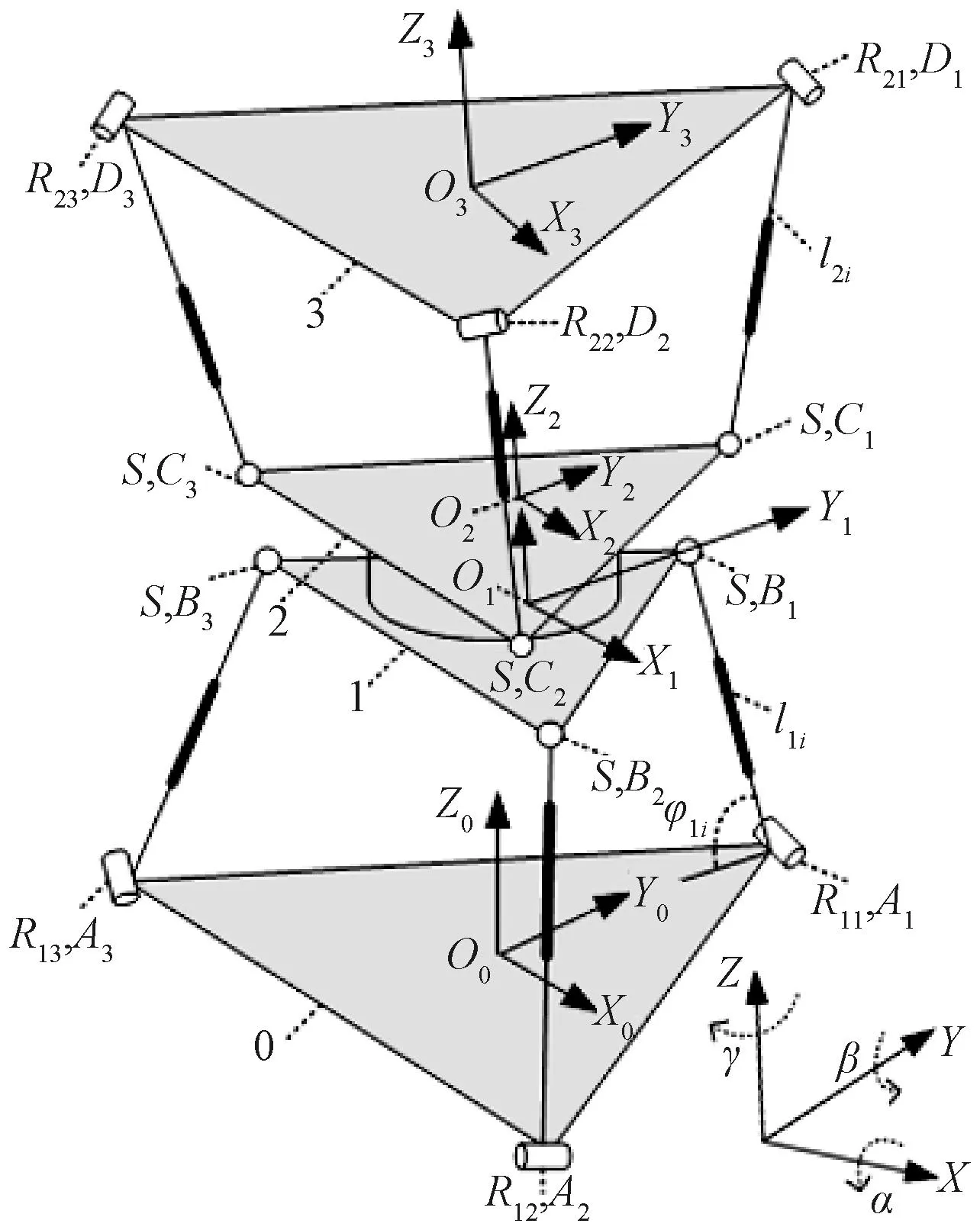
图2 3-RPS+R+3-SPR串并联机构简图Figure 2 The 3-RPS+R+3-SPR serial-parallel mechanism diagram
3-RPS+R+3-SPR结构一共有六个支链和四个平台。每个支链都是由转动副R、移动副P及球副S构成,四个平台由下至上依次记为0,1,2,3平台,各平台均是正三角形构成,中心点分别为O0,O1,O2,O3,平台0、3的外接圆半径为E,平台1、2的外接圆半径为e,在平台0上建立坐标系O0-X0Y0Z0,记作坐标系{0}。其中:X0轴平行于A2A3轴;Z0竖直向上;依据右手螺旋法则可以得到Y0轴。同理建立其他坐标系O1-X1Y1Z1,O2-X2Y2Z2,O3-X3Y3Z3,并分别记为坐标系{1},{2},{3}。下机构3-RPS的下平台端点为Ai(i=1,2,3),其上平台端点为Bi(i=1,2,3),上机构3-SPR的下平台端点为Ci(i=1,2,3),其上平台端点为Di(i=1,2,3),两个机构的上、下平台中间通过移动副P连接,下机构3-RPS的三个杆长为l1i(i=1,2,3),上机构3-SPR的三个杆长为l2i(i=1,2,3),该串并联机构的坐标轴满足如下关系:X0//A3A2,Y0⊥A3A2;X1//B3B2,Y1⊥B3B2;X2//C3C2,Y2⊥C3C2;X3//D3D2,Y3⊥D3D2。机构满足的几何约束关系有:下机构3-RPS的转动副满足R1i⊥l1i(i=1,2,3);上机构3-SPR的转动副满足R2i⊥l2i(i=1,2,3)。
2 串并混联结构的逆运动学分析
根据机构几何约束,进行位置逆解分析,位置逆解为已知动平台3的中心点位姿,求解混联机构六个驱动杆的长度。
2.1 逆运动学分析
下层3-RPS并联机构的下平台各顶点Ai在坐标系{0}中的坐标为
(1)
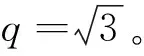
下平台各顶点Bi在坐标系{1}中的坐标为
(2)
同理,可求出上层3-SPR并联机构的下平台各顶点Ci在坐标系{2}中的坐标及上平台各顶点Di在坐标系{3}中的坐标:
(3)
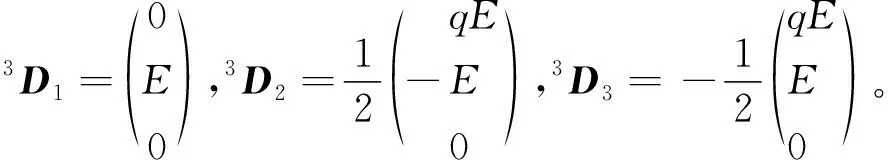
(4)
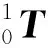
(5)
其中:
同理,上机构3-SPR的下平台各顶点Ci在坐标系{0}中表示为
(6)
其中:
θ为中间平台的旋转角度。
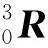
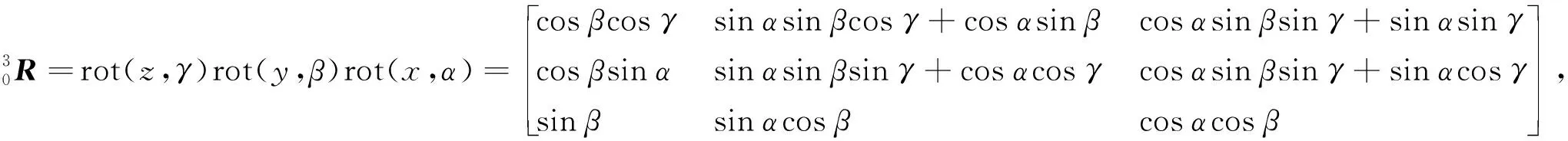
(7)
上层3-SPR并联机构的上平台各顶点Di在坐标系{0}中为
(8)
其中:
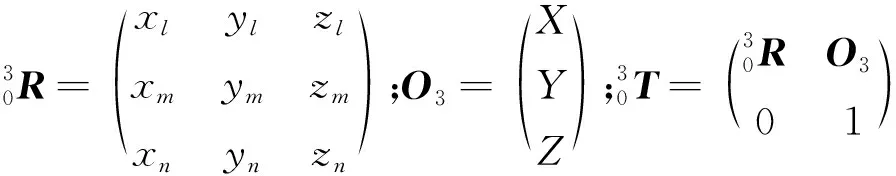
根据3-RPS和3-SPR的几何结构限制,3-RPS机构的转动副R1i(i=1,2,3)为
(9)
上层3-SPR机构的转动副R2i(i=1,2,3)为
(10)
根据并联机构的几何限制得
R1i⊥l1i(i=1,2,3)⟹R1i⊥(Bi-Ai),
(11)
R2i⊥l2i(i=1,2,3)⟹R2i⊥(Di-Ci),
(12)
代入式(11)可得
B1x=0,B2x=-qB2y,B3x=qB3y,
(13)
代入式(12)可得
(14)
则顶点Bi在坐标系{0}下为
(15)
根据顶点Bi在坐标系{0}下的坐标可以求得坐标系{0}下与{1}的变换矩阵为
(16)
(y1i+y2j+y3k)/t1,
(x1i+x2j+x3k)/t2,
z=x×y,
(17)
其中:
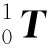
(18)
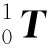
(19)
由于平台1和平台2是边长为qe的等边三角形,故满足
(20)
即
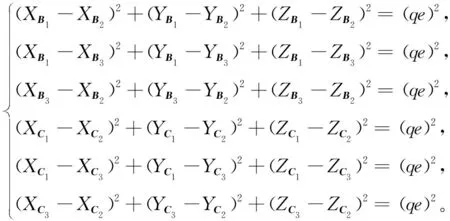
(21)
根据式(19)~(21)的九个约束方程,给定末端平台3的位姿参数X、Y、Z、α、β、γ,求解方程组,根据Bi的约束条件(13),Bi被限制在三个平面内,根据约束条件及几何限制对约束方程组的求解值进行筛选,可求出唯一的Bi坐标,利用式(6)进而求出Ci坐标。
则整个混联机构的逆解为
l1i=|Ai-Bi|,(i=1,2,3),
(22)
l2i=|Ci-Di|,(i=1,2,3)。
(23)
3 串并混联机构的正运动学分析
正运动学的求解是通过给定机构的杆长求解机构末端平台的位姿。对本文机构进行正运动学求解时,将其分为三部分,分别求出各部分的旋转变换矩阵,整体变换矩阵即为各部分变换矩阵的乘积。正解的计算采用优化算法求解,避免求解的不唯一。
3.1 3-RPS正运动学分析
对于下层3-RPS并联机构,根据其几何结构,三个转动副均沿其同平面的三角形对边平行方向布置,转动副轴线与X轴的夹角分别为0°、210°、330°。假设下层机构的各个杆与平台0的夹角为φ11、φ12、φ13,则下层3-RPS并联机构的上平台顶点Bi在坐标系{0}下的坐标为
(24)
下层3-RPS并联机构的上平台端点Bi满足式(20)。将式(24)中的Bi坐标代入,得到三个关于夹角φ11、φ12、φ13的非线性方程,求解这三个非线性方程可以使用解析法或者优化算法,解析法需要变量之间互相代换,将非线性方程转换成一元高次方程,求解过程烦琐复杂。本文采用改进的粒子群优化算法求解三个非线性方程,求解过程简便且能得到准确的结果。使用粒子群算法的步骤如下。
1) 根据三个方程构造出目标函数f1、f2、f3。
(25)
2) 确定适应度函数
F(φ11,φ12,φ13)=min|f12+f22+f32|。
(26)
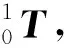
3.2 3-SPR正运动学分析
与3-RPS类似,可以将3-RPS看成3-SPR的对称机构,在对其进行正运动学建模过程中,类比3-RPS的建模方法得到动平台的3-SPR的位姿矩阵。当给出上层机构的三个杆长l2i,即可计算出夹角φ2i,可以求出上层3-SPR并联机构的位姿矩阵为
(27)
3.3 中间关节正运动学分析
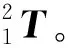
3.4 串并混联机构正运动学求解分析
正运动学总体分析过程如下:平台0和平台3之间的旋转变换矩阵为三部分:下层的3-RPS;中间的旋转关节及上层的3-SPR。三部分变换矩阵的乘积为
(28)
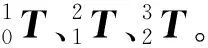
4 机构运动学仿真
通过具体的数值算例对所建立串并混联机构运动学模型进行仿真验证,验证机构正、逆运动学模型。设定机构的参数为:e=6.25 cm;E=10.25 cm;中间旋转关节高度H=10 cm。
4.1 逆运动学仿真验证
给定末端平台的位姿α=-19.059°,β=-13.001°,γ=-30.282°,X=-2.848 cm,Y=12.484 cm,Z=57.918 cm,中间关节旋转角度θ=30°。根据本文理论分析,编写Matlab程序,代入末端平台位姿,计算出混联机构的六个驱动杆杆长,见表1。
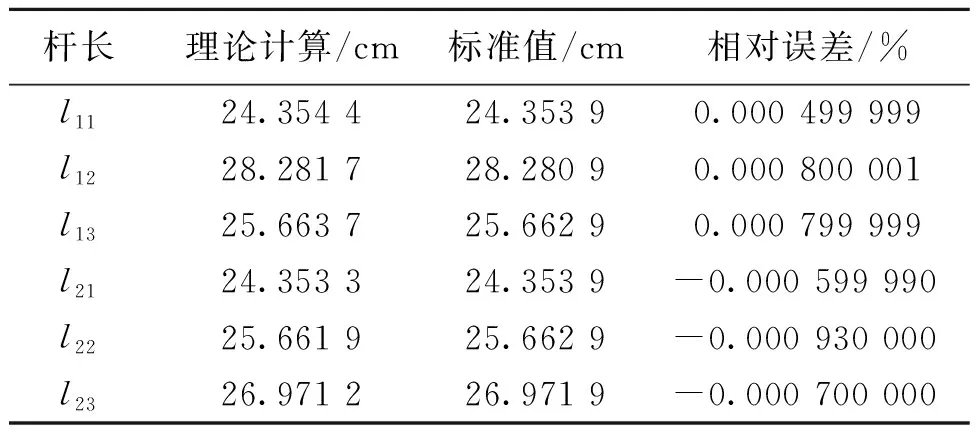
表1 3-RPS+R+3-SPR混联机构逆解算例Table 1 Inverse solution calculation example of 3-RPS+R+3-SPR hybrid mechanism
从逆解仿真验证的结果来看,将Matlab理论计算结果与标准值进行对比,其相对误差均在1×10-3范围内,验证了位置逆解的正确性。
4.2 正运动学仿真验证
在SolidWorks中建立混联机构的模型,将其导入Admas中,建立虚拟样机。添加各个关节的运动副,验证虚拟样机模型的正确性。对Admas中虚拟样机添加相应的驱动,得出正解模型的仿真结果。
对于该结构正运动学的仿真验证,其流程图如图3所示。在Adams中给六个驱动杆添加一定的驱动函数以及中间旋转关节的驱动角度,可以通过仿真得到末端平台的位姿曲线。将驱动函数导出为样条函数,并作为理论计算的输入值,通过优化算法得到末端平台位姿曲线,将两种曲线对照,如图4所示。从图4中看出,一段时间内,机构杆长的变化导致末端平台中心点位姿的变化,图4(a)~(c)分别是X、Y、Z轴方向上的移动,图4(d)~(f)是分别绕X、Y、Z轴的旋转角度变化。理论计算与仿真测量的曲线是吻合的,说明位置正解的正确性。机构在Z方向上的移动可以实现伸缩运动,绕X、Y、Z轴的旋转,X、Y、Z轴方向上的移动可以实现蜿蜒运动。
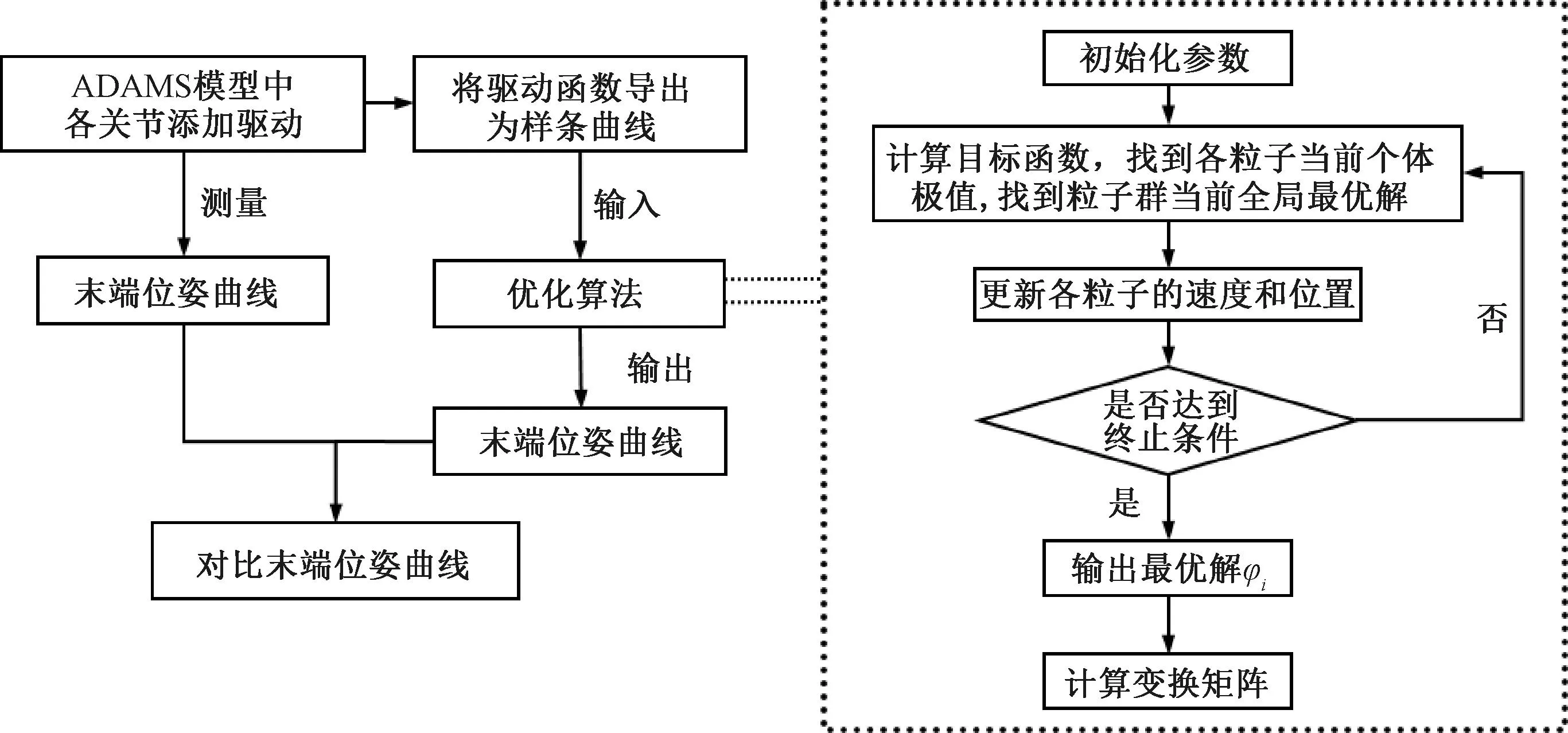
图3 正运动学仿真验证流程图Figure 3 Flow chart of forward kinematics simulation verification
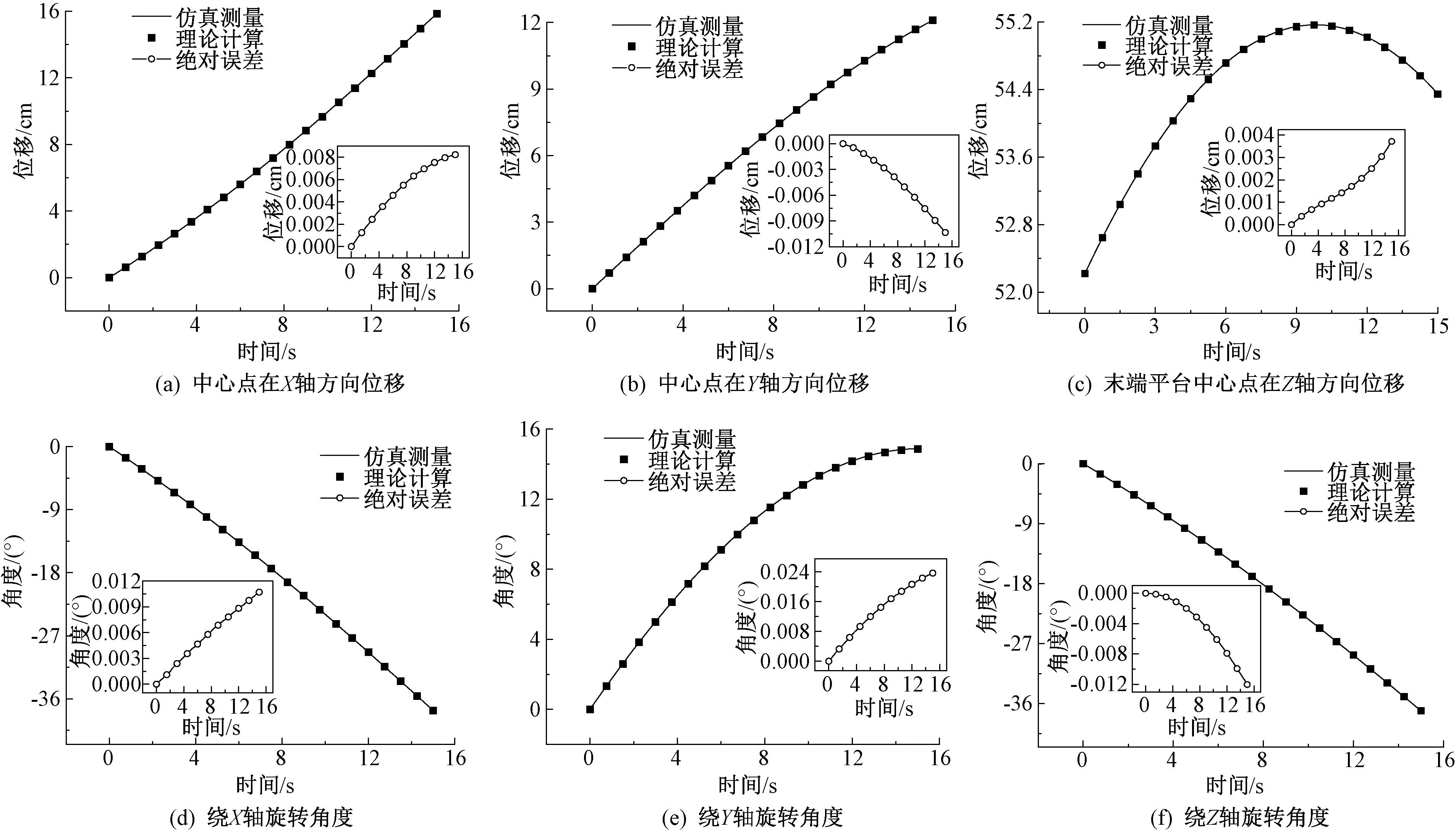
图4 末端平台位姿变化曲线Figure 4 The end platform pose change
对于本文结构的伸缩蠕动功能的仿真验证,其过程与蜿蜒运动类似,区别在于给出不同的驱动函数,使驱动杆伸长收缩来完成伸缩蠕动功能。平台0作为定平台,驱动杆通过伸长或收缩可实现平台1、2、3向前移动,在到达伸长状态后,末端平台固定,驱动杆使平台0、1、2向前收缩,完成蠕动。图5给出结构作为机器人主体帮助机器人实现蠕动功能的实例。
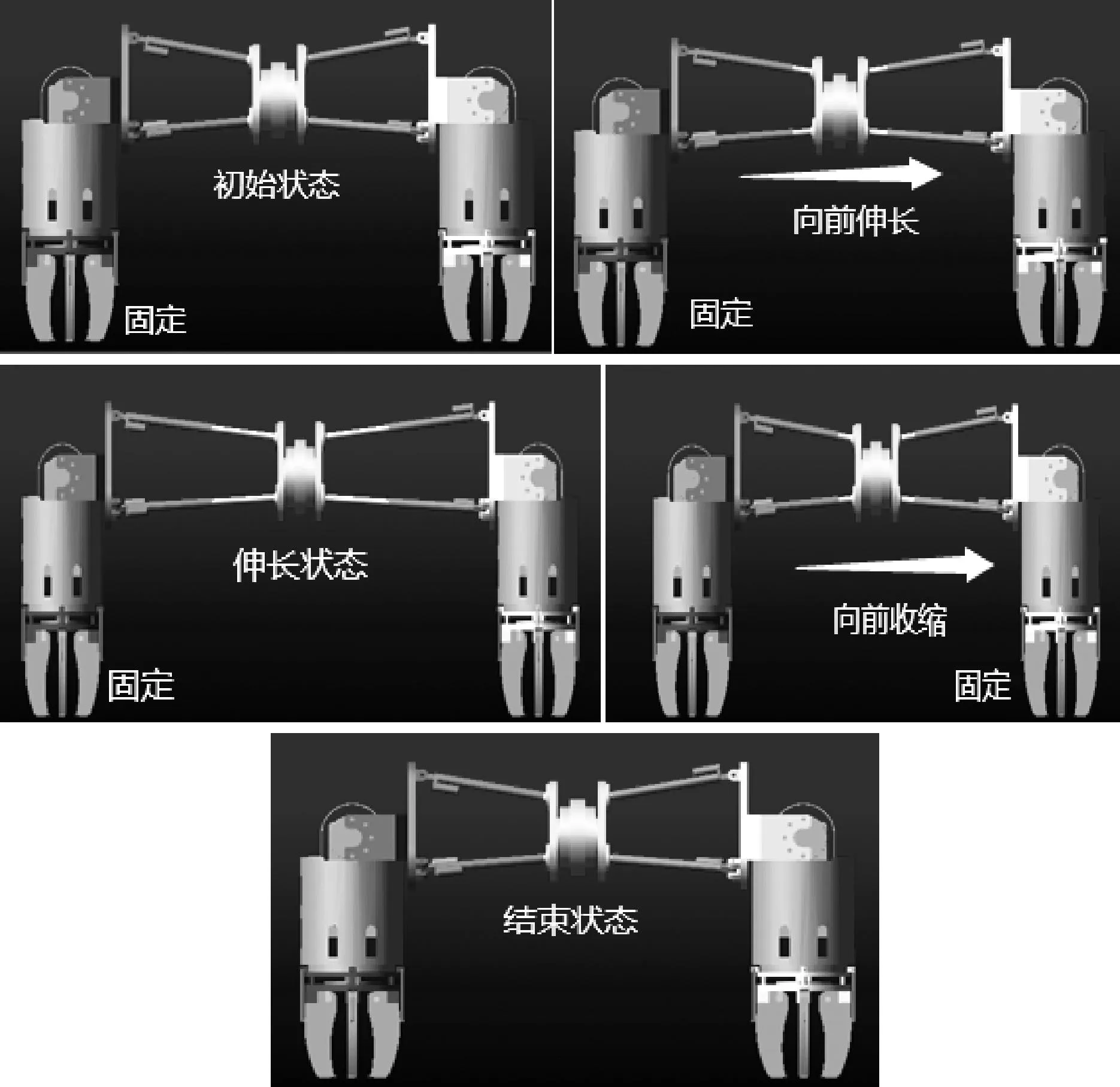
图5 蠕动步态实例Figure 5 Diagram of peristaltic gait
综上,本文机构可以实现多种运动方式,具有多运动模态功能,可以应用到工业、军事等特殊的场合。
5 结论
本文提出了一种新型3-RPS+R+3-SPR串并混联机构,该机构兼具串联和并联的优点,可实现蜿蜒、伸缩蠕动等功能。根据机构几何约束方程,建立了逆运动学模型,给出了该构型逆解的分析过程及具体数值算例。对于其正运动学正解,将整个机构分开进行分析,使得求解问题更有序,使用优化算法求解,避免了正解求解的复杂性和不唯一。最后,将利用Admas仿真测量与Matlab计算的理论模型得到的结果进行对比分析,验证了正运动学模型建立的正确性,结论表明该结构可以实现多种运动模态。

