结合邻居影响和资源分配的链路预测算法
刘英杰, 刘士虎, 高海燕, 徐伟华
(1.云南民族大学 数学与计算机科学学院 云南 昆明 650504; 2.西南大学 人工智能学院 重庆 400715)
0 引言
现实中的社交网络[1]、生物网络[2]和机会网络[3]等复杂网络不仅可以用来描述节点的属性信息,还能用于刻画节点之间的拓扑信息。因此,复杂网络因其潜在的数据信息而引起各领域学者的广泛关注。复杂网络中的研究分支主要有链路预测[4]、社团检测[5]和聚类分析[6]。其中,链路预测旨在探测节点之间存在连边的可能性。因此,链路预测具有巨大的实际应用价值。例如,在电子商务网络中使用链路预测技术为顾客推荐其喜爱的产品[7]。在犯罪网络中使用链路预测技术揭示罪犯之间隐而未现的关联关系,协助警方及时侦破案件[8]。
针对现有的链路预测问题,学者们主要采用基于节点相似性的算法来进行研究,这类算法主要分为基于局部结构的算法、基于路径信息的算法和基于随机游走的算法。
在基于局部结构的算法中,资源分配(resource allocation,RA)指标[9]和聚类系数(clustering coefficient for link prediction,CCLP)指标[10]分别在共同邻居的基础上考虑了共同邻居的度和聚类系数的影响;局部社区范式(cannistraci-resource-allocation,CRA)指标[11]在共同邻居的基础上考虑了共同邻居之间的连边数的影响。在基于路径信息的算法中,Katz指标[12]是基于两个节点之间的全路径信息的,局部路径(local path,LP)指标[13]是基于两个节点之间所有二阶路径与部分三阶路径信息的。在基于随机游走的算法中,平均通勤时间(average commute time,ACT)指标[14]基于网络中的全局随机游走而被提出。
除了上述三类算法,研究者们也提出了一系列具有代表性的算法和指标。例如,偏好连接(preferential attachment,PA)指标[15]基于节点之间连边生长的概率与节点度之积成正比的关系而被提出。矩阵森林(matrix-forest index,MFI)指标[16]利用矩阵森林理论来刻画节点相似性而被提出。CCLP2指标[17]基于二级共同邻居的聚类系数而被提出。此外,二级节点的度也被相关学者考虑在链路预测算法的设计中[18],但他们没有在拓扑性质不同的网络中对共同邻居和二级节点的影响深入分析。
值得一提的是,现有的链路预测研究还源自于网络演化中的资源传输过程[19-20]。其基本假设是两个节点之间存在资源传输,则它们之间的关系是亲密的,从而它们就更有可能相似。李英乐等[21]在RA指标的基础上,利用共同邻居周围的三角结构来量化其分配给两个节点的资源量,提出了拓扑紧密性(topological tightness,TT)指标。然而,TT指标只关注共同邻居对资源的分配,却忽略了二级节点在资源分配中的作用。
基于上述分析,为进一步探究共同邻居和二级节点在链路预测过程中的影响,本文提出了一种结合邻居影响和资源分配的链路预测算法。借助无向网络中节点之间的双向资源传输,该算法利用平衡系数来调节共同邻居和二级节点分配给两个节点的资源总量所占的比例,以探究二者在拓扑性质不同的网络中对链路预测准确率的影响。实验结果表明,在平均聚类系数高的网络中,若两个节点接收更多由共同邻居分配的资源,则可以提升链路预测的准确率;在生态网络和平均聚类系数低的网络中,若两个节点接收更多由二级节点分配的资源,则可以提升链路预测的准确率;此外,结合共同邻居和二级节点的共同影响对链路预测算法准确率的提升将更有效。
1 预备知识
1.1 复杂网络
形式上,无向复杂网络可用一个二元组G=(V,E)来表示,V表示节点集合;E表示连接任意两个节点的连边集合,即E中包含了G=(V,E)中的实际存在的边。在网络G=(V,E)中,若其内部的任意一个节点都与其余的n-1个节点相连,则G=(V,E)中共有n·(n-1)/2条可能存在的边,使用集合U来表示。于是,在G=(V,E)中的所有未知连边可用集合U-E来表示。其中,未知连边是指G=(V,E)中可能存在但尚未被探测的边。
1.2 链路预测
在进行链路预测时,按照一定的比例b(0 基于以上叙述,链路预测问题可被描述如下:对于G=(V,E)中任意一条边e,根据给定的链路预测算法为边e赋予一个相似性分数,然后将G=(V,E)中的所有可能的边都按照为它们赋予的分数进行降序排列,那么排名越靠前的连边存在的可能性就越大。 资源分配驱动的链路预测的基本原理是若两个节点之间存在资源交互,则它们的关系较为亲密,故它们更加相似,从而它们之间更有可能存在连边。 在无向网络中,节点之间的资源交互是指始发节点和终结节点可以相互向对方传输一定的资源。在这个过程中,始发节点与终结节点之间的逐阶路径上的中间节点便扮演着资源承载者的角色[21]。一般地,两个节点之间的共同邻居就是它们之间的二阶路径上的中间节点,两个节点之间的二级节点就是它们之间的三阶路径上的中间节点。下面将分别介绍两个节点之间传输的资源由共同邻居和二级节点分配时的情况。 图1分别给出了节点vx和vy之间传输的资源经由共同邻居vz进行分配时的三种情况。图1(a)表示节点vx发送的资源经由共同邻居vz平均分配给节点vy的情况;图1(b)表示节点vy发送的资源经由共同邻居vz平均分配给节点vx的情况;图1(c)表示共同邻居vz自身具有的资源被平均分配给节点vx和vy的情况。在最简单的情况下,假设节点vx和vy均向对方发送一个单位的资源被共同邻居vz分配,而共同邻居vz的聚类系数ccz被假设为它自身影响两个节点的相似性时所具有的资源量[19-20]。因此,图1中节点vx和vy在经过了双向的资源传输后能够接收1/kz+1/kz+ccz/kz=0.2+0.2+0.04=0.44单位的资源总量,其中kz为节点vz的度。 图1 资源由共同邻居分配Figure 1 Resource allocated by common neighbor 图2给出了节点vx和vy进行资源传输的过程中,资源在经由二级节点vz2被分配到节点vx和vy时的三种情况。图2(a)表示节点vx发送的资源经由二级节点vz2平均分配给节点vy的情况;图2(b)表示节点vy发送的资源经由二级节点vz2平均分配给节点vx的情况;图2(c)表示二级节点vz2自身所具有的资源被分配给节点vx和vy的情况。同样地,假设节点vx和vy向对方发送一个单位的资源被二级节点vz2分配,而二级节点vz2的聚类系数ccz2被假设为它自身影响节点vx和vy的相似性时所具有的资源量。 图2 资源由二级节点分配Figure 2 Resource allocated by second-level node 不难发现,节点之间的资源由二级节点进行分配后也会经过它们的共同邻居,但探究共同邻居和二级节点在预测过程中的影响时需要控制单一变量,故对由二级节点分配给两个节点的资源会不会因为共同邻居的影响而被稀释掉的问题,将在后续的工作中进一步讨论。本次研究在考虑资源由二级节点进行分配时,不再考虑共同邻居对资源分配的影响。以图2为例,节点vx和vy经过二级节点进行资源的双向传输后能接收1/kz2+1/kz2+ccz2/kz2≈0.25+0.25+0.042=0.542单位的资源总量。 本研究利用共同邻居和二级节点分配给两个节点的资源总量来探究它们在链路预测中的影响,并提出了一种结合邻居影响和资源分配(neighbor influence and resource allocation,NIRA)的链路预测指标。因此,考虑无向网络G=(V,E)中的任意两个节点vx和vy,vz和vz2分别是它们的共同邻居和二级节点,则NIRA的计算表达式可定义为 其中:N(vx)∩N(vy)和SN(vx,vy)分别表示vx和vy的共同邻居集合和二级节点集合,且SN(vx,vy)=[N(N(vx))∩N(vy)]‖[N(vx)∩N(N(vy))],不包括vx和vy的共同邻居;λ∈[0,1]是一个平衡系数,用于调节由共同邻居和二级节点分配给两个节点的资源比例。当λ=0时,资源只由二级节点分配给两个节点;当λ=1时,资源只由共同邻居分配给两个节点;当λ∈(0,1)时,资源由共同邻居和二级节点一起分配给两个节点。 本文的实验环境为16 GB内存,1.8 GHz速度,Windows 10操作系统和AMD Ryzen 7 4800U处理器,编程语言为MATLAB 2020a。 本文使用CCLP指标、CCLP2指标、RA指标、CRA指标、PA指标、LP指标、Katz指标、MFI指标和ACT指标作为实验的基准指标,为适用本文中的二级节点集合,CCLP2指标的计算公式也被进行了相应的扩展。下面介绍本文使用的网络数据和评价指标。 本文从公开的网络数据的学术网站上(http:∥konect.cc/networks/)收集了16个网络数据,这些网络的简称分别为LESM网络、 USAI网络、NSSM网络、KING网络、STMA网络、FWEW网络、FWMW网络、FWFW网络、ADJN网络、FORU网络、EMAI网络、UCSO网络、KARA网络、POLB网络、FOOT网络和COMM网络,它们的拓扑性质被列在了表1中,其中:n为节点数;m为边数;d为网络直径;ρ为网络密度;〈k〉为平均度;〈c〉为平均聚类系数。 表1 网络的拓扑性质Table 1 Topological properties of networks 本文使用受试者工作特征曲线下的面积(area under curve,AUC)值和精确度(Precision)进行评价,它们的定义分别如下。 AUC值为随机地从测试集中选择一条边的相似性分数比从不存在边集中选择一条边的相似性分数更高的概率。若在t次的分数比较中,有t1次是测试边的分数大于不存在边的分数,有t2次是二者分数相等,则AUC的值被定义为 其中:t被设置为10 000,衡量算法的性能。 Precision为排名靠前的边被准确预测的比例,即在排名前L的边中,若有l条边是测试集中的边,则Precision计算为 Precision=l/L, 其中:L被设置为100,衡量算法的性能。 为探究NIRA指标的预测性能以及适用范围,本文分析了NIRA指标与基准指标在多个网络中的AUC值和Precision值。下面先分析NIRA指标的可行性。 图3为NIRA指标在16个网络中随着平衡系数λ的变化而生成的AUC曲线和Precision曲线。由图3(a)可知NIRA指标的AUC曲线具有以下两个特点。 当λ∈(0,1)时,NIRA指标的AUC值在所有网络中都达到了一个峰值点。这表明当共同邻居和二级节点一起分配资源给两端节点时,NIRA指标可以取得最优AUC值。在共同邻居和二级节点的共同影响下,NIRA指标的AUC值达到了最优。 NIRA指标的AUC曲线在λ=0和λ=1处存在着较大的差异,在拓扑性质不同的网络中表现得更明显。如在LESM、USAI、NSSM和KING中,NIRA指标在λ=1时的AUC值远远大于其在λ=0时的AUC值,而在ADJN、FORU、EMAI、UCSO、STMA、FWEW和FWFW中,又呈现出相反的情况。这表明,在平均聚类系数较高的网络中,共同邻居对NIRA指标的AUC影响大于二级节点;然而二级节点在平均聚类系数较低的网络和部分生态网络中对NIRA指标的AUC影响大于共同邻居。此外,在FWMW、POLB、FOOT和COMM等网络中,共同邻居的影响在提升NIRA指标的AUC上比二级节点更加具有优势。 由图3(b)可看出NIRA指标的Precision曲线与其AUC曲线具有相同的变化趋势。即在LESM、USAI、NSSM、KING这4个平均聚类系数较高的网络和POLB、FOOT、COMM等网络中,共同邻居对NIRA指标的Precision的影响大于二级节点;在STMA、FWEW、FWMW、FWFW这4个生态网络和ADJN、FORU、UCSO等三个平均聚类系数较低的网络中,二级节点对NIRA指标的Precision的影响更大。然而,在EMAI网络中,共同邻居对NIRA指标的Precision的提升更有优势。此外,NIRA指标在NSSM、KING和FOOT网络中的最优Precision值均在λ=1处。因此,在这三个网络中,共同邻居对相应算法的Precision的提升更有优势。这表明,在多数网络中考虑共同邻居的影响来提升算法的Precision是可行的。上述的实验结果表明,从资源分配的角度描述 图3 NIRA指标在平衡系数λ影响下的AUC和Precision曲线Figure 3 The AUC and Precision curves of NIRA index with the influence of balance parameter λ 共同邻居和二级节点在链路预测中的影响是可行的。 表2和表3为NIRA指标与基准指标之间的AUC值和Precision值,表中每一行的加粗数字为在该网络中最高值。 表2 NIRA指标与9个基准指标之间的AUC值比较Table 2 Comparison of the AUC values between the NIRA index and nine benchmark indices 由表2中的结果可知,CCLP指标和CCLP2指标在拓扑性质不同的网络中的预测性能表现出较大的差异。在LESM、USAI、NSSM和KING网络中,CCLP指标比CCLP2指标的AUC值提升了7.47%~29.6%;然而在STMA、FWEW、FWFW、ADJN、FORU、EMAI和UCSO等网络中,CCLP2指标比CCLP指标的AUC值提升了2.84%~17.44%。 从CCLP指标和CCLP2指标的AUC值可以看出,仅考虑了共同邻居或二级节点的单一影响难以使得相应的算法在拓扑性质不同的网络中展现出较好的性能。结合了两类邻居共同影响的NIRA指标不仅实现了普适性,在准确率方面也有大幅度提升。此外,相比RA指标和CRA指标,NIRA指标在较多的网络中取得了最高AUC值,这表明考虑资源的双向传输是更有效的。PA指标在四个生态网络中表现良好,但在其余网络中均不如NIRA指标。LP、Katz、MFI、ACT等指标的预测效果相对较好,但除了FOOT网络中的MFI指标,其余三个指标在剩下的15个网络中的AUC值均不如NIRA指标。 表3 NIRA指标与9个基准指标之间的Precision值比较Table 3 Comparison of the Precision values between the NIRA index and nine benchmark indices 由表3可知CCLP指标和CCLP2指标的Precision值与它们的AUC值具有相同现象。由此可见,仅考虑共同邻居或二级节点的单一影响的确难以保证算法的普适性。值得一提的是,考虑共同邻居影响的算法似乎更适合用Precision来评价,如RA指标在NSSM和POLB网络中取得了最优Precision值,而CRA指标在EMAI和FOOT网络中也取得了最优的Precision值。在大多数网络中,CCLP、RA和CRA指标相比PA、LP、Katz、MFI和ACT等也都取得了更高的Precision值。 在本文中,利用算法在各个网络中运行时消耗的时间来分析它们的时间复杂度。为此,本文将算法a在网络b中运行时所消耗的时间归一化到区间[0, 1]来进行更为直观的分析。此外,考虑基于局部结构的链路预测算法具有较低的复杂度,本文只在节点数大于800的网络上分析Katz指标、MFI指标、ACT指标、NIRA指标和CCLP2指标的时间复杂度。 表4给出了Katz、MFI、ACT、NIRA和CCLP2等五个指标在KING、FORU、EMAI和UCSO网络中的归一化时间消耗。从表4中的结果可以看出,NIRA指标相比于CCLP2指标在运行时间上也具有一定的优势,但相比其余三个基准指标,NIRA指标却是在牺牲了一定的计算时间后换来性能上的提升。这是因为在构造NIRA指标和CCLP2指标的过程中,需要先找出两个节点之间的二级节点集合,而这一步骤需要在MATLAB编程软件中利用两个for循环来完成,故NIRA指标和CCLP2指标的运行时间增加了。 表4 五个指标的归一化时间消耗Table 4 Normalized time consumption of five indices 单位:s 为了探究共同邻居和二级节点在链路预测中的影响,本文借助节点之间的双向资源传输,通过利用两个节点接收由它们的共同邻居和二级节点分配给它们的资源总量来度量它们的相似性。实验结果表明,在平均聚类系数较高的网络中,两个节点接收更多由共同邻居分配给它们的资源时,链路预测效果更佳;在平均聚类系数较低的网络和生态网络中,两个节点接收更多由二级节点分配给它们的资源,链路预测效果更佳;在拓扑性质不同的多个网络中,结合两类邻居的共同影响而提出的算法不仅具有较高的预测准确率,还实现了良好的普适性。 本文在后续的研究中将探究共同邻居和二级节点之间的其余子节点对于提升链路预测算法性能的影响,从而进一步优化本文所提出的预测模型。2 资源分配驱动的链路预测
2.1 基于共同邻居的资源分配
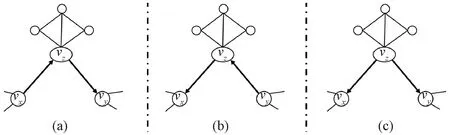
2.2 基于二级节点的资源分配
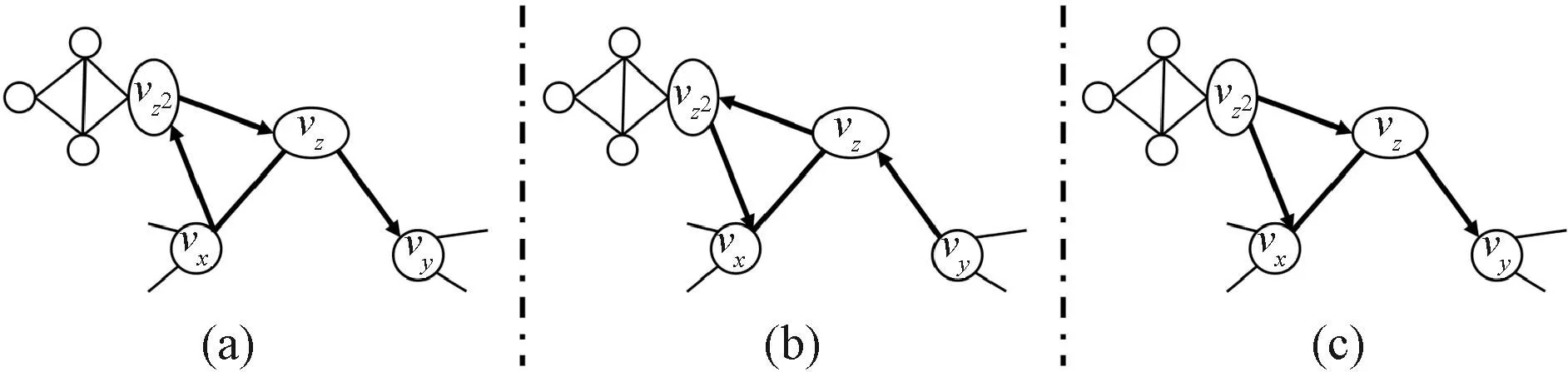
2.3 邻居影响下的资源分配链路预测指标
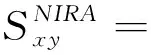
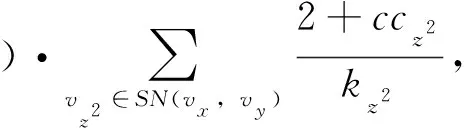
3 实验设置
3.1 网络数据
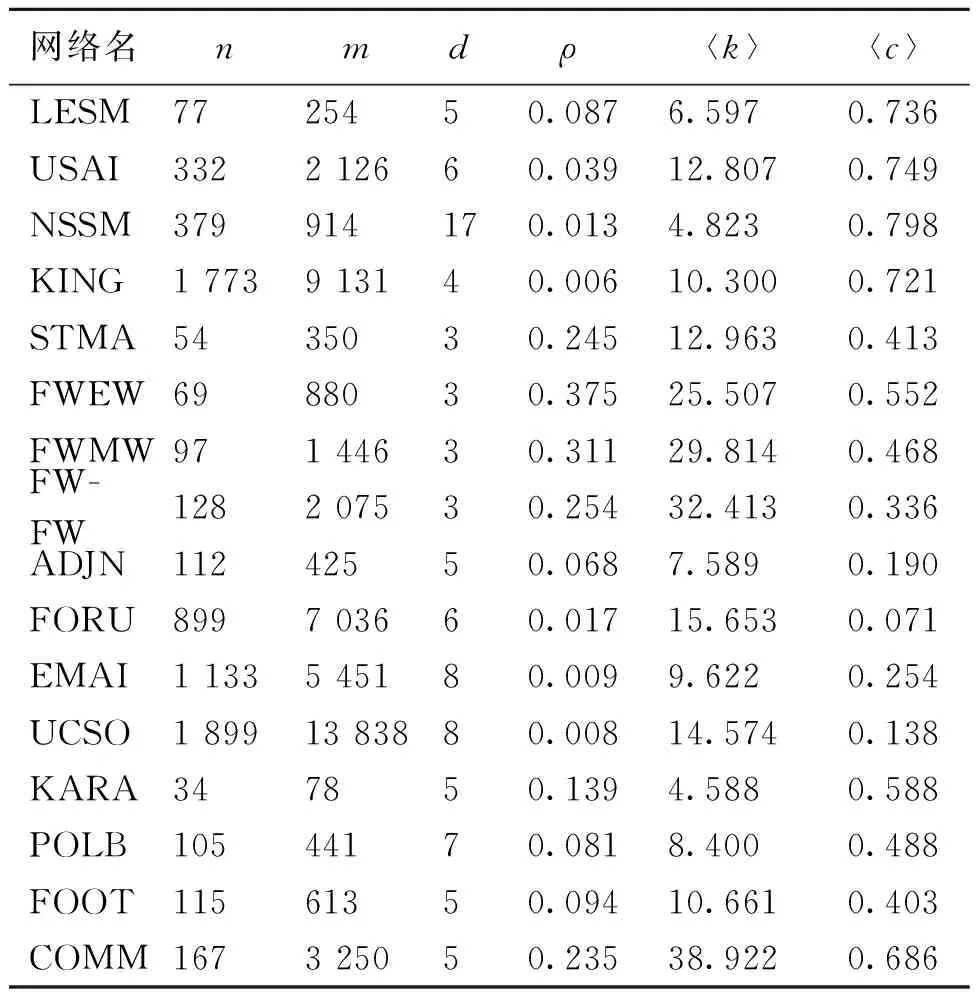
3.2 评价指标
4 算法验证及结果分析
4.1 可行性分析

4.2 有效性分析
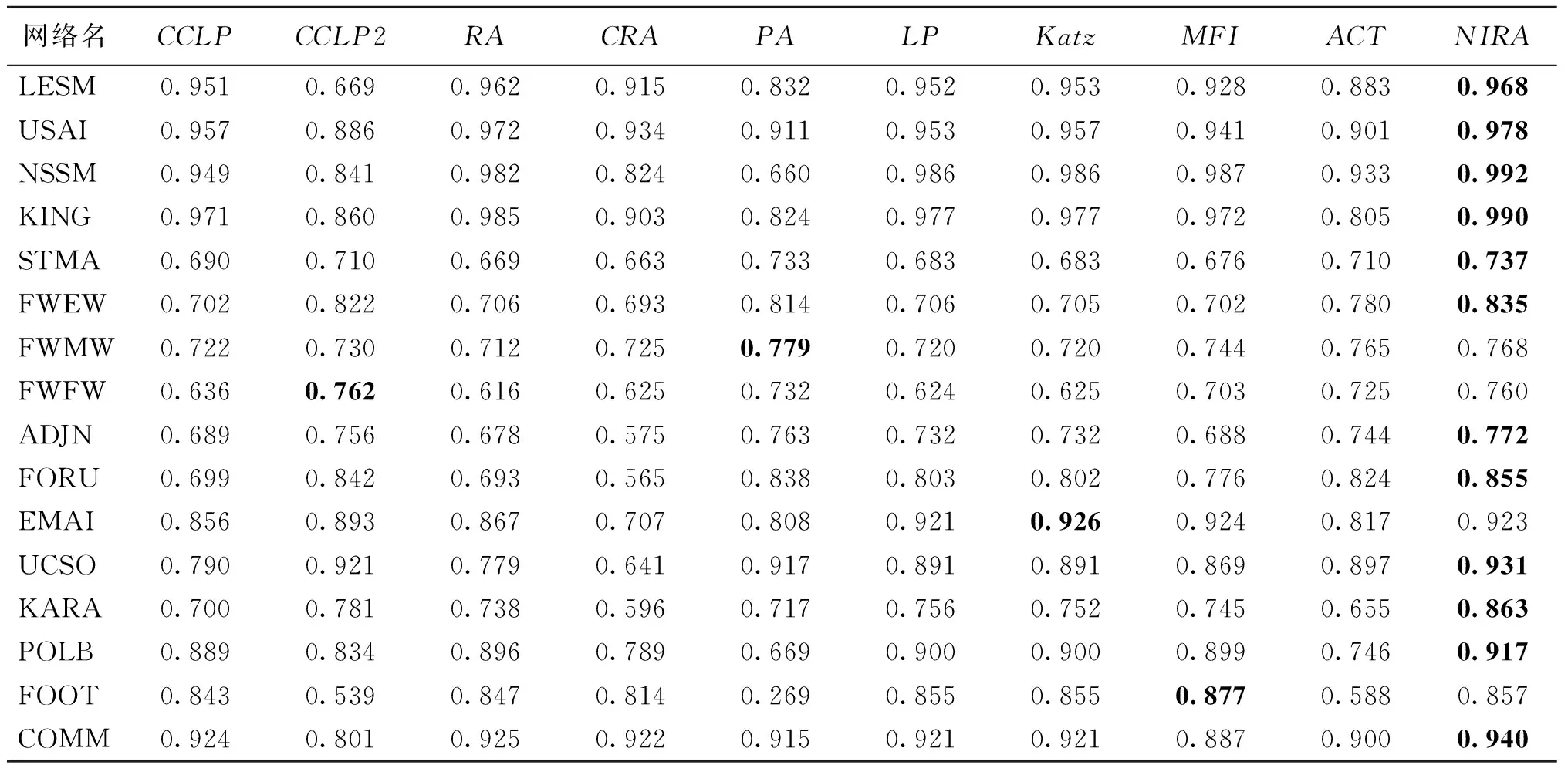
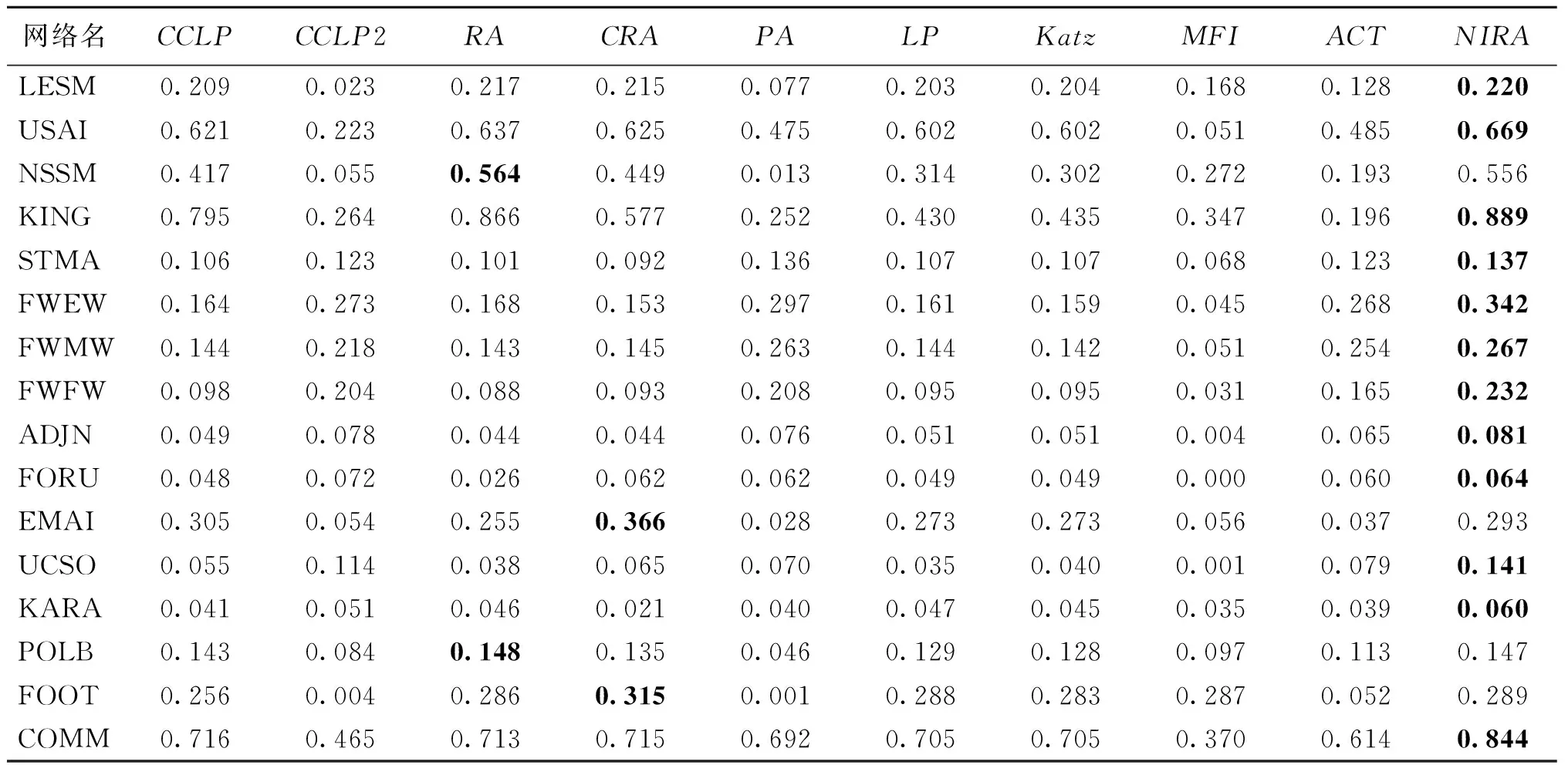
4.3 复杂度分析
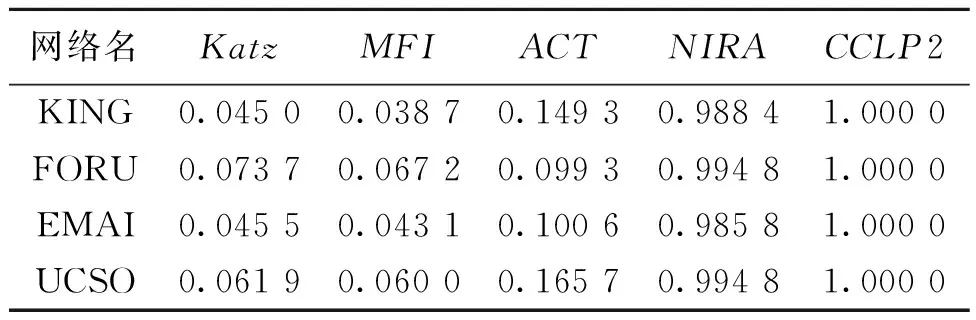
5 结论

