基于视觉伺服的自动对接技术研究

王樟平,楼佩煌,钱晓明,张沪松,张 悦

(1.南京航空航天大学机电学院,江苏 南京 210016)(2.南京航空航天大学苏州研究院,江苏 苏州 215000)

导弹装填与挂载等作业频率高、危险性大、劳动强度大,自动对接技术能够很好地解决以上问题。自动对接技术最早应用于航天器的空间交会对接[1],后来发展到大型零部件在制造过程中的装配对接领域。自动对接技术通过位姿检测装置识别设备间的位姿偏差,并控制运动执行机构自动完成偏差收敛,直至设备完成对接。其中的位姿检测设备如激光跟踪仪、iGPS成本高昂,且系统安装后只能固定于室内使用[2]。如何开发一套可用于室外移动作业的自动对接平台,是目前亟待解决的问题。

工业相机体积小、检测精度高,适合作为移动作业条件下的位姿检测设备。视觉伺服技术使用视觉信息构建闭环反馈自动控制系统[3],相较于由单张图片计算位置偏差的方法,其可以实现对目标的动态跟踪。并联六自由度调姿平台刚性大、精度高、承载能力强,典型的Stewart平台构型已有相当丰富的运动控制技术研究历史,适合用于自动对接平台的快速开发。

本文将双目相机和并联机构分别作为位姿检测设备和运动执行机构,基于视觉伺服技术开发了一套可移动挂载大型零部件的自动对接平台。提出了存在外界干扰时的视觉伺服终止判定依据,建立了并联机构运动控制模型,通过坐标变换方法实现双目相机伺服控制速度与并联机构位置控制量的转换,并给出实验论证。

1 自动对接平台设计

为满足移动挂载作业需求,本文设计的自动对接平台分为主动对接机构和被动对接机构。主动对接机构由AGV(automated guided vehicle,自动导引运输车)承载,由并联机构、包含双目相机在内的各类位姿检测传感器以及待对接零件组成。被动对接机构固定在挂架上,包含用于锁紧零件的装置。此硬件布局方案完成了传感器、待对接零件以及挂架的分离,适用于零件挂载作业场景。

自动对接平台结构如图1所示。待对接零件放置在并联机构动平台上时可自行定位,双目相机通过立柱固定于并联机构动平台,在自动对接过程中,相机的观察对象为被动对接机构。工作时,主动对接机构由AGV运载至目标位置附近,随后系统启动,将待对接零件自动对接并挂载至目标挂架上。

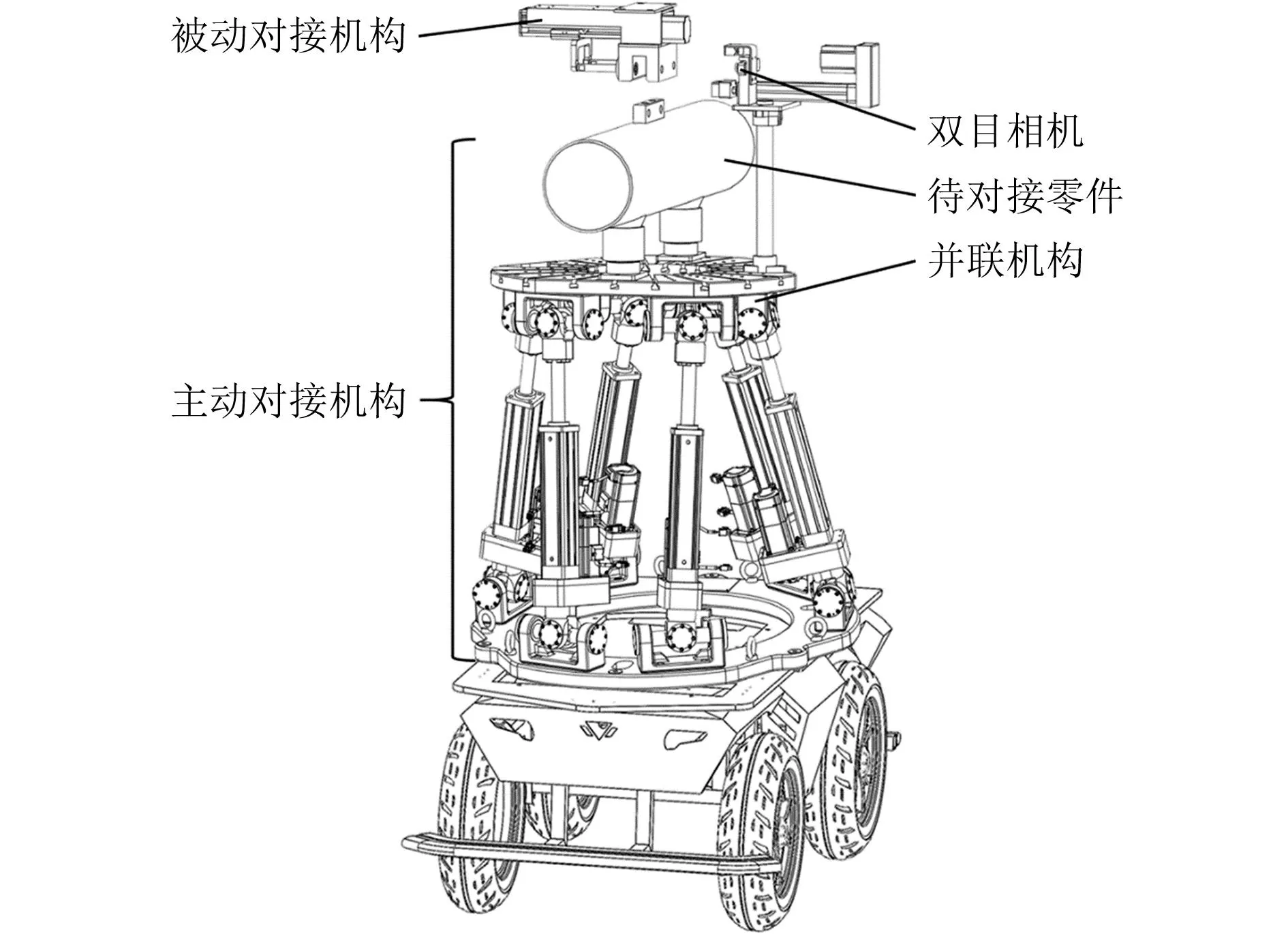
图1 自动对接平台结构示意图

2 基于视觉伺服的自动对接技术

基于视觉伺服的自动对接技术需要解决3个关键问题:一是选定合适的图像特征点并开发相应的特征提取算法;二是通过视觉伺服技术将图像特征点坐标转换为伺服控制量,通常直接获得的是相机的伺服控制速度;三是将相机的伺服控制速度转换为并联机构的位置控制量。此外还需解决移动作业环境中存在干扰时的伺服终止问题。限于篇幅,本文不对图像特征提取算法做详细介绍。本文将论述相机模型与基于图像的视觉伺服技术原理,提出系统存在干扰时的伺服终止判定依据,并推演并联机构的运动控制模型。

2.1 相机模型

常见的针孔相机将三维世界中的坐标点映射到二维图像平面上的过程可以用针孔模型描述[4],相机镜头前的物体反射的光线通过镜头光心投影到相机内部的感光传感器即成像平面上,形成一个倒立的实像。其成像原理如图2所示。

图2 针孔相机成像模型

设OXYZ为相机坐标系,O为相机镜头光心,相机前方空间中一点A在相机坐标系中的坐标为(X,Y,Z),经光心O投影后,在物理成像平面O′X′Y′形成投影点B,光心O与成像平面之间的距离为焦距f。为方便模型的计算,将成像平面按照投影关系对称地设置在相机正前方,即图中的成像平面X″Y″Z″,形成投影点C。物体成像最终经相机感光元件采样成为像素图像,为此在成像平面上引入图像坐标系OPuv。A点坐标与投影点C的像素坐标可由以下变换关系表示:

(1)

式中:Puv为投影点在图像坐标系中的齐次坐标,u、v分别为投影点在图像坐标系中的横纵坐标;K为相机的内参数矩阵,其参数fx,fy,cx,cy可通过相机标定获得;PN为投影点在相机坐标系中Z=1处归一化平面上的齐次坐标,如图2中Oxy坐标系所在平面。通过式(1)可将特征点的图像像素坐标转换为归一化平面坐标。

2.2 基于图像的视觉伺服技术

2.2.1控制原理

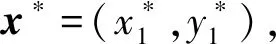
e=x-x*

(2)

视觉伺服的控制目标即为缩小偏差e直至收敛。

设特征点在相机坐标系中的坐标为X=(X,Y,Z),此时相机具有伺服控制速度VC=(vC,wC),其中vC为伺服控制线速度,wC为伺服控制角速度,两者存在如下关系:

(3)

将式(3)按坐标量分解,得:

(4)

式中:vx、vy、vz为vC在相机坐标系中分解后的各坐标分量,wx、wy、wz为wC在相机坐标系中分解后的各坐标分量。

特征点归一化平面上的坐标与其在相机坐标系中的坐标有如下关系:

(5)

对式(5)求导后将式(4)代入,得:

(6)

式中:Lx∈2k×6,为特征雅可比矩阵,其中k为选定的图像特征点个数,其定义了特征点归一化平面坐标与相机伺服控制速度的变换规则。

-λe=LxVC

(7)

该方程具有极小最小二乘解[6]:

(8)

(9)

式中:Lx1、Lx2、Lx3、Lx4分别为特征点坐标x1、x2、x3、x4的特征雅可比矩阵。

计算特征雅可比矩阵还需获得特征点在相机坐标系中的深度信息Zd。设空间中一点在双目相机左右视野中存在视差p,双目相机的基线长度为b,镜头焦距为f,则可直接由三角形相似原理计算出空间点的深度信息:

(10)

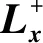
(11)

在完成目标位置标定的基础上,通过式(11)即可由当前图像计算出相机的伺服控制速度。

2.2.2伺服终止判定依据

在无外界干扰、系统正常工作时,通常应使用误差函数的收敛性质作为伺服是否到达目标位置的判定依据。如使用误差向量e的1范数定义伺服终止判定条件:

‖e‖1≤ε1

(12)

式中:ε1为通过实验测定的伺服终点位置处‖e‖1的上限。而实验表明,当自动对接作业中存在机械振动、环境光干扰时,可能会导致上述判定条件失效,如‖e‖1稳定在一个比ε1更大的数值,导致视觉伺服过程无法终止。为此,本文提出使用‖e‖1的方差作为伺服终止的辅助判定条件。假设系统从最新一帧图像上计算获得的误差向量的1范数为‖ec‖1,此前的(n-1)帧图像分别有误差向量1范数‖ec-1‖1,‖ec-2‖1,…,‖ec-n+1‖1,设n个误差向量1范数的算术平均数为μe,计算n个误差向量1范数的方差S2为:

(13)

由于方差表示数据的波动情况,当误差向量逐渐收敛并趋于稳定时,其方差S2将趋近于0。于是,为伺服终止增加另一条判定条件:

S2<ε2

(14)

式中:ε2为误差向量收敛时允许的最大数据波动。结合式(12)与式(14)定义的判定条件,在满足设备安全的情况下为ε1设定较大的值,如本文通过实验测定的伺服终点位置处‖e‖1上限约为一个10-3数量级的值,而在程序中设定ε1=1×10-6,将ε2设定为较小的值,如本文选定ε2=1×10-6,当两个条件同时满足时,可认为伺服到达终点位置,此时终止视觉伺服流程。

此伺服终止判定条件在一定程度上提高了视觉伺服系统的抗干扰能力,在实验中取得了良好的效果。

2.3 并联机构运动控制模型

图1所示双目相机安装时与并联机构动平台固连,选择双目相机任一视野图像进行视觉伺服,设该视野镜头的相机坐标系为OCXCYCZC,设并联机构动平台坐标系为OPXPYPZP,坐标原点OP位于动平台上表面中心,ZP垂直指向上方,两坐标系之间的相对位置关系如图3所示。为简化速度变换关系的推导,将两坐标系的安装位置关系设置为坐标轴两两平行:ZC∥YP,XC∥XP,YC∥ZP,原点OC和OP间的偏置如图3所示,分别为a,b,c。设相机在当前时刻的伺服控制速度为VC=[vCx,vCy,vCz,ωCx,ωCy,ωCz]T,根据两坐标系的空间位置关系,可写出并联机构动平台的控制速度为VP=[vPx,vPy,vPz,ωPx,ωPy,ωPz]T,其中:

(15)

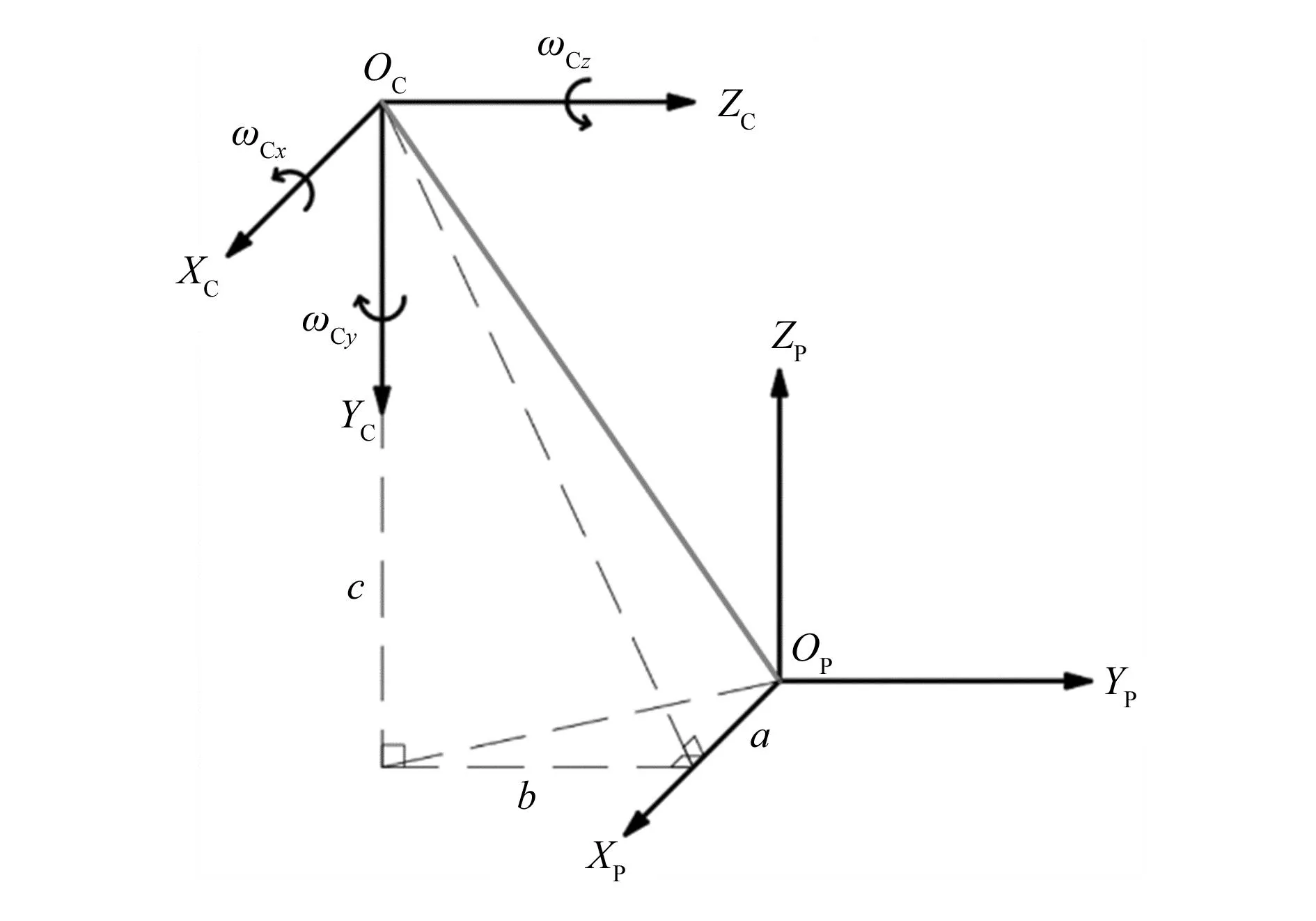
图3 相机与并联机构动平台坐标系位置关系图

VC,VP均为在世界坐标系中定义的运动速度。

为驱动并联机构,还需将其动平台的伺服控制速度转换为位置控制量。并联机构各坐标系间的变换关系如图4所示。

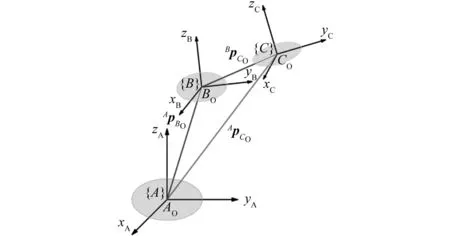
图4 并联机构坐标变换关系示意图

图中{A}为并联机构基坐标系,与定平台固连,{B}、{C}均为并联机构动平台坐标系,定义{B}为动平台在当前时刻所处位置的坐标系,{C}为下一时刻将要运动到的位置的坐标系,三者的坐标原点为AOBOCO,可写出并联机器人运动学方程:

(16)

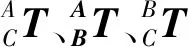
并联机构采用Z-Y-X欧拉角进行姿态控制,假设并联机构动平台在位置{B}处的伺服控制量为[xB,yB,zB,αB,βB,γB]T,其中xB,yB,zB分别为沿并联机构动平台坐标系X,Y,X轴的位移控制量,αB,βB,γB分别为绕X,Y,Z轴的角度控制量,则可写出坐标系{B}相对于{A}的齐次变换矩阵:

(17)

式中:c代表cos,s代表sin。

并联机构动平台处于位置{B}时的伺服控制速度可由式(15)计算获得。由于相机每获取一帧图像时会重新计算伺服控制速度,因此每次迭代动平台仅能运动一段微小距离。设动平台在微小时间δt内以速度VP从{B}位置运动到{C},可得{C}的坐标原点CO在{B}坐标系中的位置为:

BpCO=[vPxδt,vPyδt,vPzδt]T

(18)

而VP中的瞬时角速度为坐标系{B}相对于其自身三坐标轴的转速,因此由坐标系{B}到坐标系{C}的姿态变换可由R-P-Y角表示,设坐标系{B}先绕XB旋转wPxδt,再绕YB旋转wPyδt,最后绕ZB旋转wPzδt变换为坐标系{C}的姿态,此过程的旋转变换矩阵可记为:

Rot(X,wPxδt)

(19)

式中:Rot(·)为基本旋转变换矩阵。组合式(18)与式(19)即可获得坐标系{C}相对于坐标系{B}的齐次变换矩阵:

(20)

通过式(17)与式(20)可求得坐标系{C}相对于坐标系{A}的齐次变换矩阵,假设有如下值:

(21)

式中:rij代表通过上述步骤求得的矩阵元素具体值。

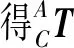
(22)

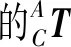
3 自动对接实验

自动对接平台进行对接作业之前,需要在伺服终点位置处对目标图像进行标定,随后视觉伺服使用此处标定的特征点坐标计算误差向量。本文标定获得的目标图像上4个关键特征点像素坐标为:

PD=

其中每一列为一个特征点的像素坐标。自动对接平台启动时,相机测得的相应特征点初始像素坐标为:

PB=

随后,特征点的当前像素坐标与期望像素坐标误差在伺服控制下逐渐收敛,同时主动对接机构在并联机构驱动下逐渐接近被动对接机构,直至两者完成对接。视觉伺服结束时测得的特征点像素坐标为:

PE=

求得4个特征点在视觉伺服结束位置PE与标定位置PD的平均坐标偏差为0.714像素,根据双目相机内参及目标距离相机镜头的位置,换算成机构的对接位置偏差为0.051 mm,能有效满足高精度对接需求。

在实验时记录中间点坐标,拟合出的关键特征点在成像平面上的运动轨迹如图5所示。其中虚线框的4个顶点为特征点在视觉伺服开始时的位置,实线框顶点则为结束时位置,带箭头实线为特征点的运动轨迹。图5表明系统对接时几乎按最短路径运动,轨迹平滑,控制效果良好。

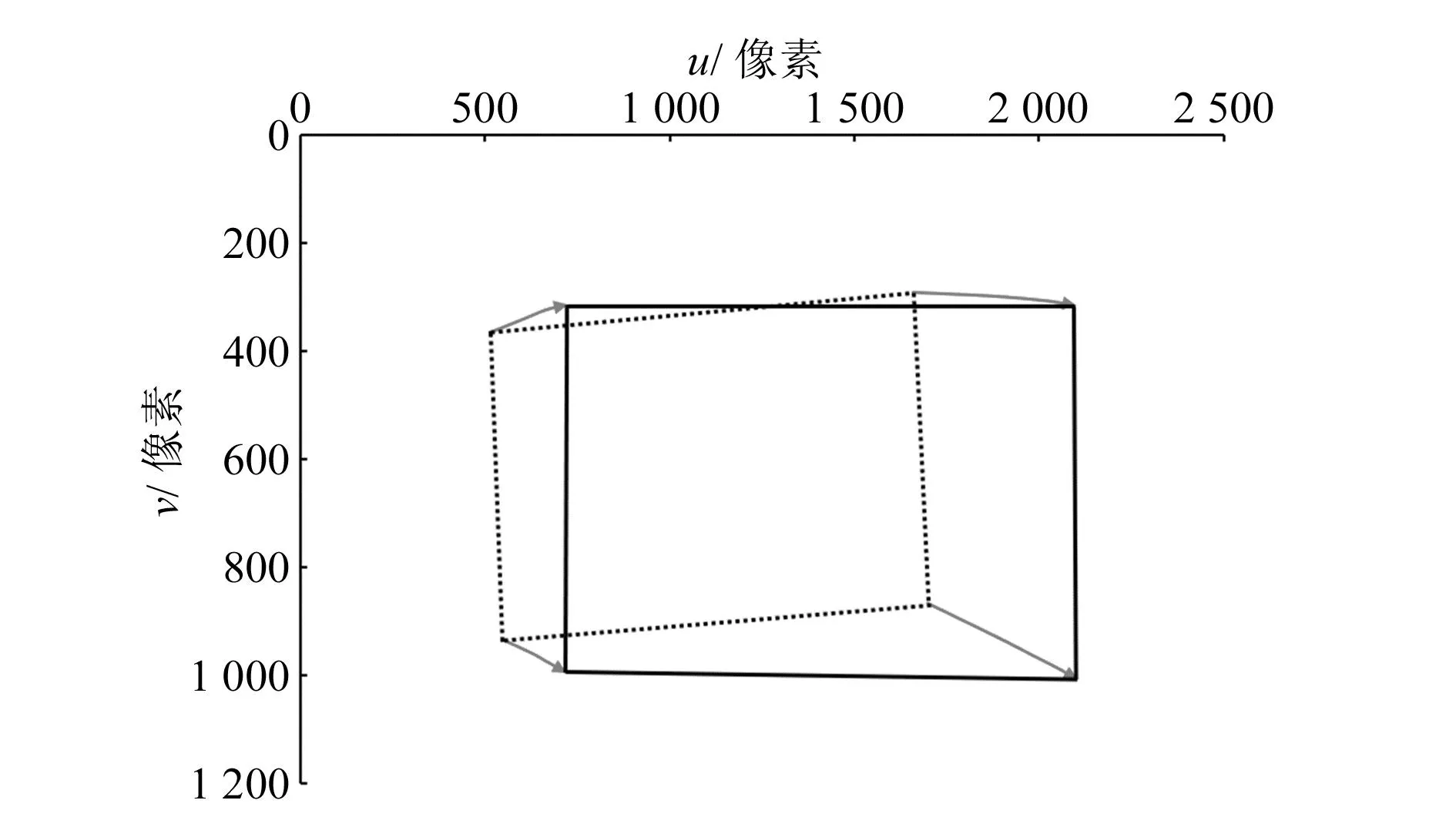
图5 自动对接过程中特征点运动轨迹

本文通过控制AGV的位置,调整主动对接机构和被动对接机构的初始位姿偏差,分别在不同初始位姿偏差时进行对接实验,并在实验中记录并联机构的当前位置与目标位置的偏差,绘制出的系统对接位置偏差收敛趋势图如图6所示。

图6 位置偏差变化趋势

图6代表了5种具有不同初始位姿偏差的系统对接过程,由图可知,偏差曲线的收敛过程平滑,并未出现超调或振荡的情况,系统能够稳定且快速地完成对接。

此外,为检验自动对接平台在存在外界干扰时的作业能力,在系统进行自动对接的过程中调整AGV位置以引入干扰,记录实验过程中位姿偏差的变化,如图7所示。图中L,M,N三点为扰动施加点,其中L,M两点处施加与伺服运动方向相反的干扰,N点处施加与伺服运动方向同向的干扰。由图可知,视觉伺服系统对干扰具有良好的动态消除能力,只要系统并非一直处于受外界干扰的振荡状态,并且干扰未导致伺服目标位置超出并联机构工作空间,系统就能正常完成对接。

4 结束语

本文基于视觉伺服技术设计的可用于大型零部件挂载的自动对接平台,具备对目标特征的动态跟踪与系统移动作业能力。基于双目相机的深度感知功能推导了并联机构运动控制方法,提出了存在外界干扰时视觉伺服终止判定条件。通过坐标变换方法实现了双目相机伺服控制速度与并联机构伺服控制速度的转换,并基于积分思想将并联机构的速度控制量转换为位置迭代控制量。实验结果表明,本文研发的自动对接平台对接精度高,抗干扰能力强,能满足移动对接作业需求。