三平移4PPa-2Pa并联机构运动学分析与优化设计

夏蓉花,刘艳梨

(1.江苏安全技术职业学院智能制造与应急装备学院,江苏 徐州 221000)(2.南京航空航天大学机电学院,江苏 南京 210016)

三平移并联机构与六自由度并联机构相比,具有控制简单、结构紧凑[1]、设计成本低的特点,因此在工业应用领域具有广阔应用前景[2-3]。近年来,越来越多的学者对三平移并联机构展开研究。孔一啸等[4]设计了一种应用于移印机领域的空间三平移2-CPR/UPS并联机构。沈惠平等[5]提出了一种具有位置正解解析式且运动部分解耦的空间三平移并联机构。史素敏等[6]设计了一种结构紧凑的3UPRR并联机构,并提出了一种利用综合性能指标作为尺度优化的优化目标。Hraiech等[7]提出了3-UPU平动并联机器人的多目标优化设计方法,可推广应用在其他类型机器人的优化设计中。程强等[8]设计了一种新型正交三平移3-CPR并联机构,基于ADAMS软件进行样机运动仿真,同时研究机构操作空间性能[9],结果表明机构具有较好的运动性能,以工作空间体积作为优化目标可得到最优的结构尺寸参数解。

本文以三平移4PPa-2Pa并联机器人机构为研究对象,根据方位特征集综合方法验证机构运动性质,并建立运动学方程数学模型,在此基础上对机构的运动学正逆解算例进行验证。采用数值法研究机构任务工作空间形状和大小,以给定的任务工作空间为目标优化函数,实现参数的最优化设计。

1 并联机构设计

1.1 机构模型

图1为4PPa-2Pa并联机构结构简图,静平台上分布着两条支链,每条支链和静平台通过移动副Pi1、Pi2相连接,Pi1、Pi2共用一个导轨,且其上各布置一个平行四边形机构Pai1、Pai2。Pai1、Pai2共用一个短边,和短边垂直的方向上布置一个平行四边形机构Pai3,Pai3所构成的平面垂直于公共短边,且和动平台相连接。动平台固定在平行四边形机构Pai3的短边中点上。建立的4PPa-2Pa关联机构三维模型如图2所示。定义如下参数:r为动平台半径,R为静平台导轨之间距离的一半,l1为移动副所在导轨长度,l2为上部平行四边形机构Pai1、Pai2的杆长,l3为下部平行四边形机构的Pai3杆长。

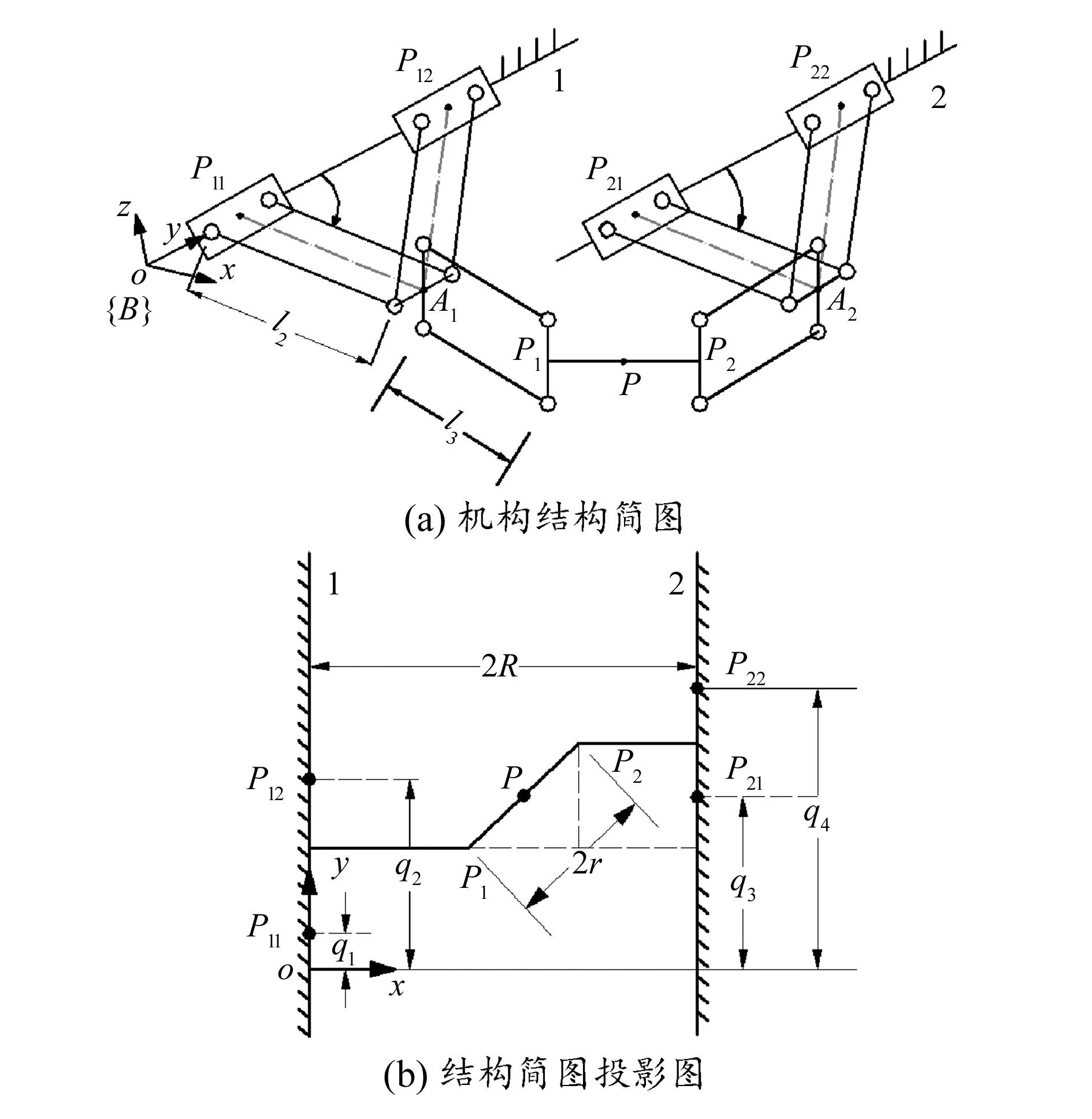
图1 4PPa-2Pa并联机构结构简图

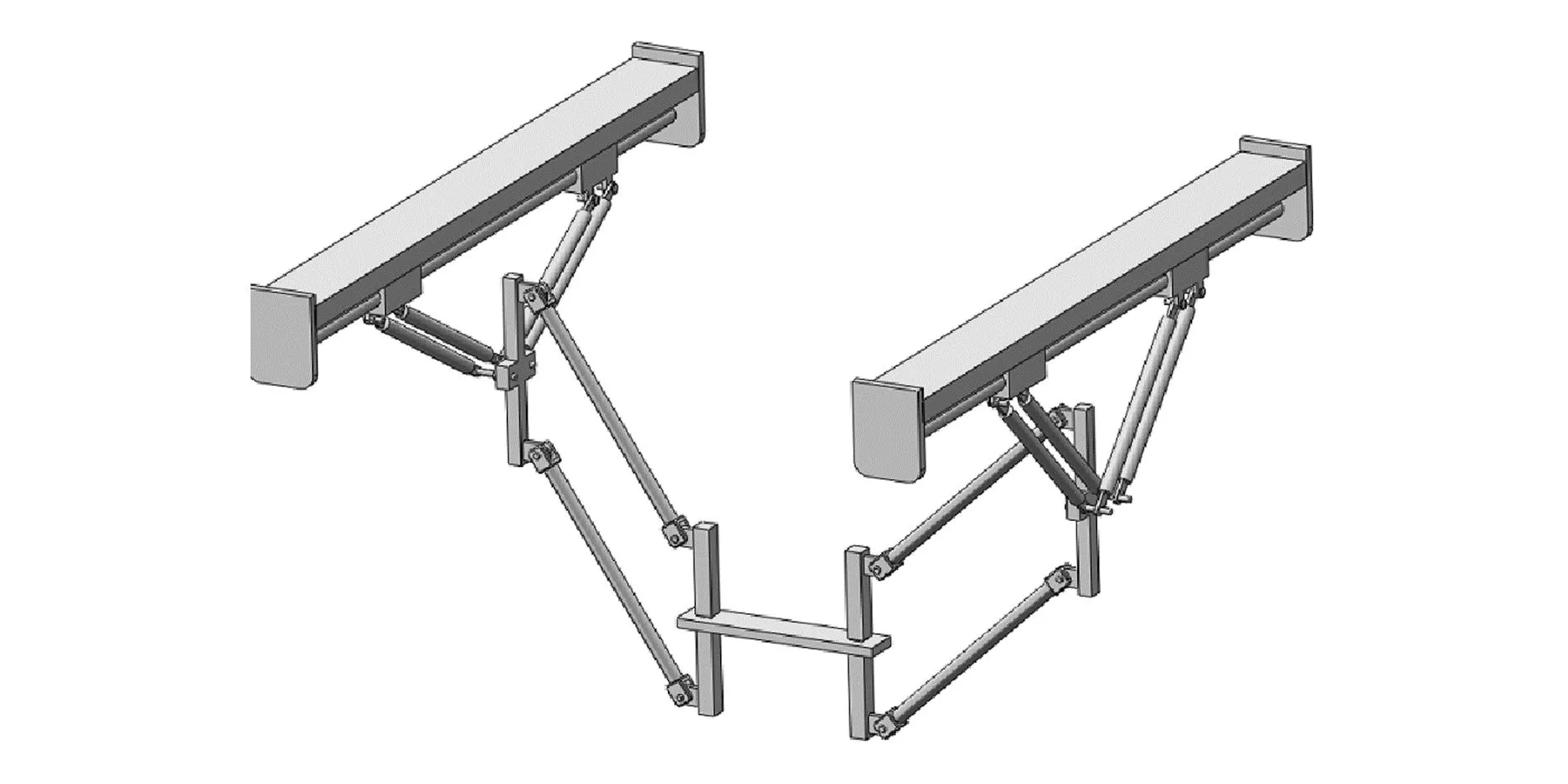
图2 4PPa-2Pa并联机构的三维模型

1.2 拓扑特性分析

根据机构描述可得运动副间位置关系,计算每条支链的方位特征集Mbi:

(1)

式中:t表示移动副,r表示转动。

1)计算由支链1和2构成的位移方程数ξL1:

ξL1=dim{Mb1∪Mb2}=

(2)

2)计算4PPa-2Pa并联机构的方位特征集Mpa:

(3)

3)计算4PPa-2Pa并联机构自由度F:

(4)

式中:m为机构运动副数量;v为机构独立回路数量,v=m-n+1,其中n为机构运动副构件个数;fi为支链第i个运动副的自由度个数;ξLj为第j个独立回路的位移方程数。

以上分析表明,4PPa-2Pa并联机构具有空间x、y、z方向三平移运动性质,能满足预期的运动特性要求。

2 位置分析

定义静平台上的移动副Pi1、Pi2的输入位移均为(q1,q2,q3,q4),通过执行末端输出P(x,y,z)推导出输入位移(q1,q2,q3,q4)的过程为逆解求解过程,反之,利用输入位移(q1,q2,q3,q4)计算得到执行末端的输出即为正解求解过程。

2.1 位置逆解分析

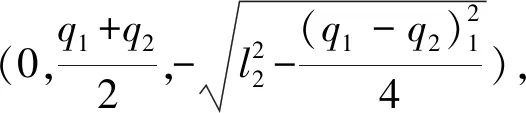
定义动平台的参考点为P,设P点坐标为(x,y,z),可得到平行四边形的短边杆中点与动平台的连接点P1、P2坐标,即(x-r,y,z)、(x+r,y,z)。由于动平台和平行四边形机构Pai3刚性连接,因此P1、P2以及A1、A2沿着xoy平面的投影共线,故可得到以下方程组:

(5)

另外,平行四边形机构Pai3短边中点长度恒定不变,由此可得以下关系:

(6)

代入坐标可得:

(7)

综合式(5)、(7),推导得到以下运动学方程:

(8)

根据式(8)计算出位置逆解(q1,q2,q3,q4)表达式:

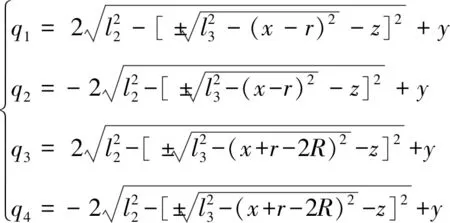
(9)

上述分析表明,位置逆解最多存在16组解。

对式(9)进行算例分析,输入几组(x,y,z),求解出满足条件的正实数解(q1,q2,q3,q4),其中4组见表1。

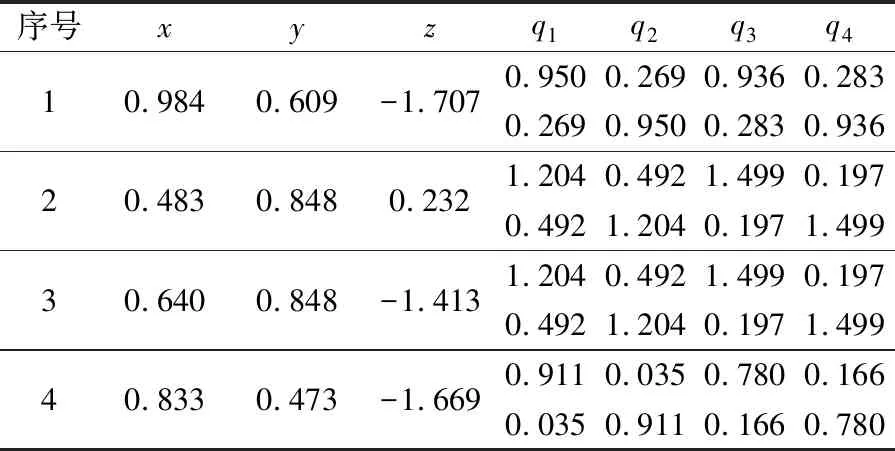
表1 4组逆解的数值解

2.2 位置正解分析

已知(q1,q2,q3,q4)求解(x,y,z),根据表2的数值,反过来求解位置正解,见表2 。

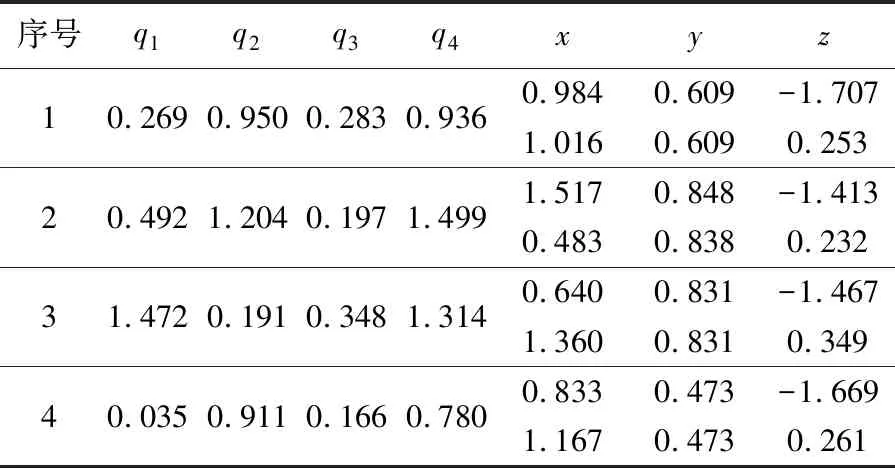
表2 4组正解的数值解

从表1和表2可以看出,逆解数值解和正解数值解相对应,检验了机构运动学分析的正确性。

3 工作空间分析

工作空间搜索方法有很多,通常采用极限搜索法[10],即根据建立的运动方程模型进行搜索[11]。并联机构具体尺寸参数值见表3。

表3 并联机构的结构参数值 单位:m

分析图3所示工作空间可知:工作空间呈心形柱状,内部无空洞,整体工作空间大,连续对称分布。

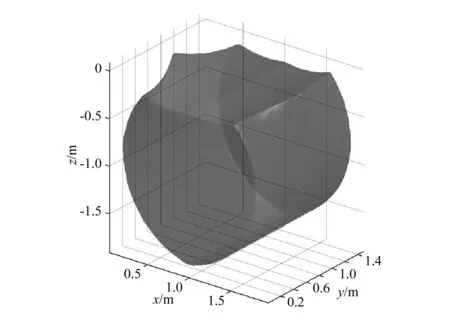
图3 4PPa-2Pa机构工作空间图

4 并联机构优化设计

针对给定任务工作空间机构尺度约束条件下的优化问题,在满足给定任务工作空间前提下寻找较小的尺寸参数。约束条件下,目标函数可以根据需要优化的参数直接建立,也可以和优化的参数间接建立。

4.1 优化模型的建立

为设计方便,根据图3的工作空间估计其中心点为(1,0.8,-0.9),给定的任务工作空间大小参考文献[12]中数据,其中任务工作空间为长方体或者球体,优化模型如下:设计优化参数{R,r,l1,l2,l3},使机构的工作空间包含形状为长方体或球体的任务工作空间,并且使机构体积较小。

4.2 模型优化目标函数的建立

本文提出一种包含关系约束的数学模型:以给定的任务工作空间内的一点C作为出发点,分别计算C点到任务工作空间的边界点Bi(i=1,2,…,s)的距离L2ij,其中s为任务工作空间边界点个数,C点到机构工作空间边界点Aij(i=1,2,…,s′;j=1,2,…,k)的距离L2ij,其中s′为射线个数,k为射线i穿过的边界点个数,为保证点Aij和点Bi的对应关系,CBi和CAij在一条从C点出发的射线上,同时为避免机构边界全部在给定工作空间的一侧,C、Bi、Aij需均匀分布于平面或者三维空间中,那么包含关系可定义为如下的不等式:

(10)

式中:n=∞。实际计算中,取n为较大的球,对所有点都成立,则机构工作空间包含任务工作空间;若存在一点不满足公式(10),则机构工作空间不包含任务工作空间。特别是当公式(10)等于0时,表明给定任务工作空间和机构工作空间恰好相切。

包含关系的模型示意图如图4所示。虚线为给定任务工作空间边界,实线是机构工作空间边界,在工作空间两个边界中间有空洞情况,从点C出发的两个射线L1、L2分别交于给定任务工作空间点B1、B2和机构工作空间点A11、A12、A21、A22,根据公式(10)计算可得:CB2-CA21<0,CB2-CA22<0,CB1-CA11>0,CB1-CA12<0,显然此时机构工作空间不包含给定任务工作空间。

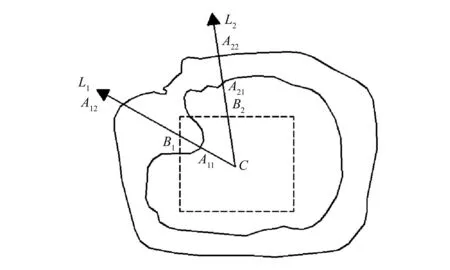
图4 包含关系的模型示意图

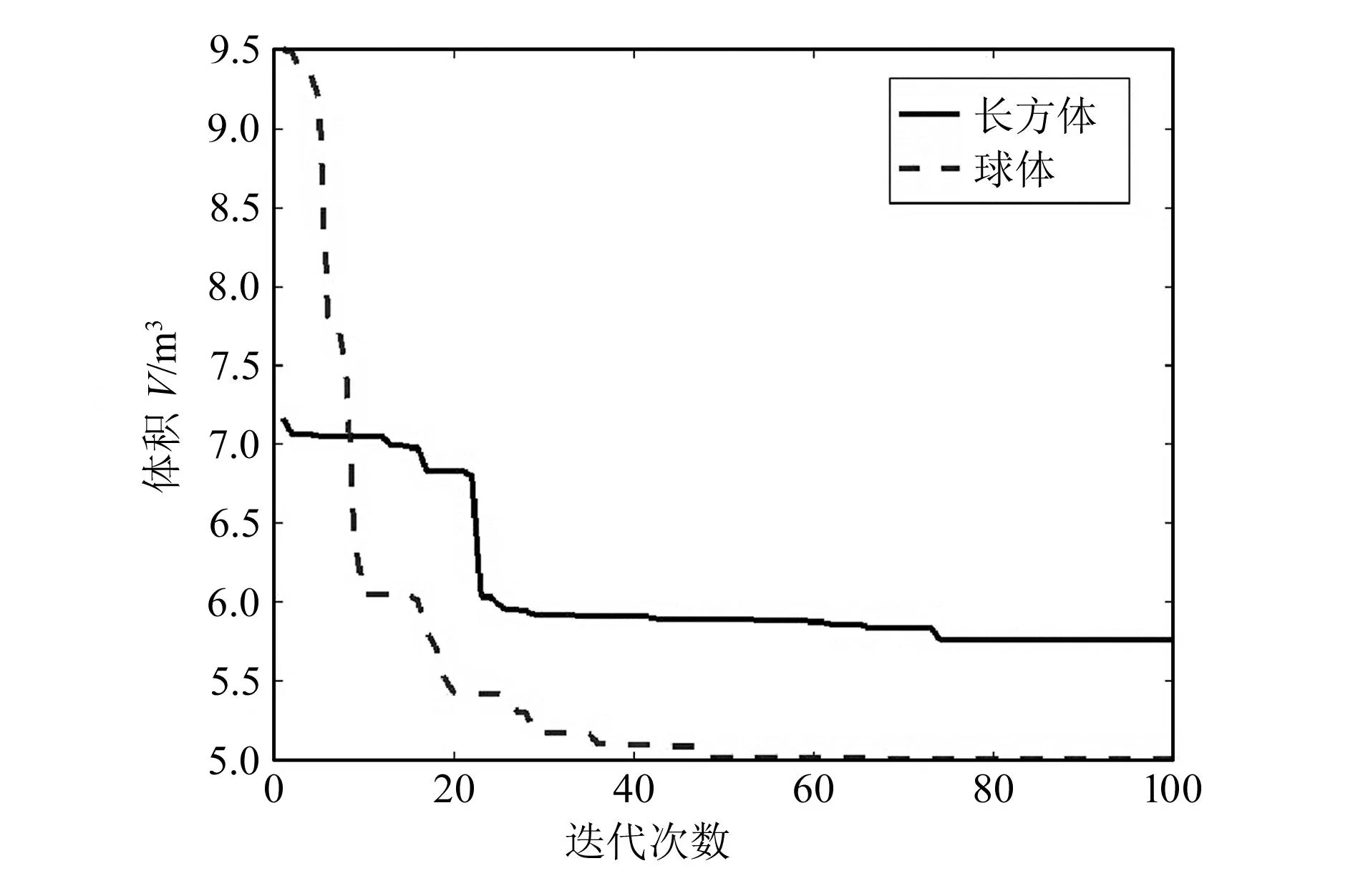
图5 长方体和球体的任务工作空间体积优化曲线

根据式(10)建立优化目标模型:

minf(R,r,l1,l2,l3)=fitness

s.t.L1i-L2ij≤0i=1,2,…,s,

j=1,2,…,k

(11)

式中:fitness为想要优化的目标函数。

可以通过罚函数法将任务工作空间优化问题转化为无约束优化问题,设f(R,r,l1,l2,l3)为目标函数,则:

(12)

式中:μ为一较大的正数,设定为比目标函数值最大值大得多的数。

4.3 优化算法选择

边界点搜索算法目标函数设计:采用球面坐标法完成对机构不同参数下工作空间的搜索[13],从中心点增加半径,对搜索球面进行约束判断,当上一半径的约束从1变成0,或者从0变成1时,记录发生突变的约束逻辑值为1的边界点坐标值;从C点出发至机构边界点Aij形成射线簇,此射线簇与给定任务工作空间边界相交于点Bi,根据公式(10)计算各边界点到中心点的距离,同时定义目标函数如下:

(13)

式中:V为工作空间体积。

选择遗传算法完成优化目标的搜索[12,14],参数见表4,适应度计算采用排序法,选择随机遍历抽样算法,利用分散重组方式,分别对两种给定任务工作空间下的两种目标函数进行优化,求其约束下的最小值。参数取值范围见表5。

表4 遗传算法参数

表5 机构结构参数取值范围 单位:m

4.4 优化结果分析

根据建立的目标函数模型,通过MATLAB得到优化曲线,如图4所示,相对应优化参数值见表6。优化目标在100代左右都降低到了比较理想的值。以球体为例的工作空间体积V优化结果为5.1 m3,以长方体为例的工作空间体积V优化结果为5.9 m3,此时给定的任务工作空间在工作空间内占比最大。分析表明,优化后机构工作空间的利用率更高,从而使并联机构控制更灵敏。

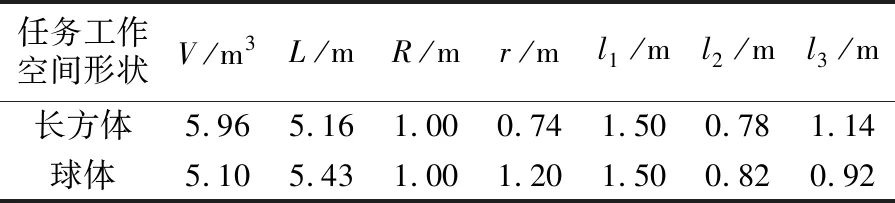
表6 优化参数值列表

图6和图7是优化后机构工作空间和给定任务工作空间的空间位置图,以球体和长方体为例,在以体积V为优化目标的情况下,任务工作空间被工作空间紧密包络在内部,分布紧凑,工作空间利用率高。算例表明:不同任务工作空间优化效果都十分显著,工作空间利用率明显提升,验证了优化模型的正确性,同时对于复杂并联机构工作空间和多种优化目标,该模型有效且简单,能够适应不同机构给定任务工作空间的约束优化问题。

图6 以球体为例的工作空间和给定任务工作空间的空间位置图

图7 以长方体为例的工作空间和给定任务工作空间的空间位置图

5 结束语

本文以纯移动并联机构作为研究对象,提出了一种空间三平移并联机构,拓扑结构分析证明机构具有空间三维移动的运动特性,基于矢量法建立非线性方程组,计算机构的位置正解和逆解,同时根据数值法研究机构的工作空间性能。分析了结构参数对工作空间的影响趋势,建立了给定任务工作空间约束问题的数学模型,通过智能优化算法完成结构参数最优解的计算,验证了模型的正确性,表明该机构具有较好的应用前景。