基于GPU 的实景三维模型裁剪算法研究

马东岭，李铭通，朱悦凯

(山东建筑大学测绘地理信息学院，山东 济南 250101)

0 引言

倾斜摄影是遥感和测绘领域近年来发展起来的一项高新技术[1]。 基于倾斜影像生成的实景三维模型已经广泛应用于测绘、 地理信息系统(Geographic Information System，GIS)、环境应用、城市和土地管理、灾害与应急、三维地图服务和三维导航等领域[2]。 然而，倾斜影像密集匹配的点云非常密集，所生成的模型包含成千万甚至上亿个点，给三维模型的应用带来极大的不便，因此通常采用“分层分块”构建多细节层次(Levels of Detail，LOD)模型的方式处理，即利用裁剪窗口对模型多次裁剪和简化[3]。 LOD 的裁剪在倾斜摄影三维模型应用中有着重要作用。 目前，常用的基于逐边裁剪思想的方法使用多个裁剪器进行裁剪，在凸多边形裁剪中可以准确地获得想要的多边形。 然而，该方法涉及编码计算、求交计算和多边形三角化3 个方面，因此大量的计算会导致算法时间效率不高。

多边形裁剪算法是在电脑图形和图像处理领域中最为基本、使用最多的算法之一，在实景三维模型裁剪中的应用范围也越来越广泛[4]。 Bae 等[5]提出了端点编码(Cohen–Sutherland)算法，实现了快速检测完全在裁剪区域内或外的线段，减少了求交计算数据量，但在复杂情况下会进行多次不必要的计算。 基于该编码思想，Sutherland 等[6]提出的多边形裁剪(Sutherland－Hodgman)算法使用了分而治之的策略，将裁剪操作分解为裁剪窗口的一条边裁剪原始多边形的一条边，使用多个裁剪器进行裁剪，该方法在凸多边形裁剪中具有极高的效率与高度的并行性[7]。 而在复杂多边形裁剪研究中，陈国军等[8]提出一种可以裁剪凹多边形、多连通多边形以及自相交多边形的裁剪算法，可将复杂多边形分解为简单的凸多边形，并根据顶点与裁剪窗口拓扑关系裁剪。

裁剪后将会得到由一组有序顶点表示的多边形，在LOD 裁剪中需要将其分解为三角形集合，并入裁剪后的三角网格结构。 因此，需要对顶点序列进一步三角化，进而构建Mesh 网。 多边形三角化是代数拓扑学里最基本的研究方法[9]。 在三角化众多算法中最常使用的是狄洛尼三角化(Delaunay Triangulation)算法，其遵循“最小角最大”和“空外接圆”规则，通过有约束三角化生成含有内嵌边界的三角网格模型。 虽然此方法适于裁剪多边形的三角化，但存在约束条件繁琐、运行效率低的问题[10]。相比之下，Eberly[11]提出的耳切三角化算法有着易实现、效率高的特点，其算法思路为找出多边形的耳朵构造一个三角形，剔除多边形的顶点数组中对应顶点，递归执行以完成裁剪。

多边形裁剪和三角化算法多是基于中央处理器(Central Processing Unit， CPU)处理，随着裁剪次数的增加，其算法的耗时呈线性增长趋势，计算效率较低。 但同时，多边形裁剪与三角化均属于计算密集型任务，并行性高，因此适合并行化加速。 近年来，随着制程工艺和集成技术的发展，图形处理器(Graphic Processing Unit， GPU)的计算能力越来越强大[12]。 为适应倾斜摄影三维模型LOD 快速裁剪的需求，文章利用GPU 的并行计算能力，提出了一种基于统一计算设备架构(Compute Unified Device Architecture，CUDA)的实景三维模型裁剪算法。 其将CPU 算法划分为大小相同的子任务，以满足并行编程的需要；再设计了一个多级索引结构，将数据映射到CUDA 线程，保证一个线程处理一个三角面，避免读写冲突的同时保证线程间负载均衡；在不影响裁剪网格质量的前提下，使用几种策略提升算法性能，并将GPU 裁剪并行算法应用于LOD 裁剪实验，以期在保证算法裁剪精度的同时，显著提高三维模型的裁剪效率。

1 CUDA 并行计算架构

CUDA 是一种操作GPU 计算的硬件和软件架构，是建立在NVIDIA 的GPUs 上的一个通用并行计算平台和编程模型[13]。 GPU 由若干个流多处理器(Streaming Multiprocessor，SM)组成，每个SM 由若干个流处理器(Streaming Processor，SP)、存储器、控制逻辑和少量的其他计算单元组成[14]。 每个SP 都是独立的运算单元。 CUDA 架构能够将计算量均衡、灵活地分配到执行单元SM 上，适合数据并行的计算密集型任务。 GPU 结构如图1 所示，线程(Thread)是GPU 最小的执行单元，大量的线程被组织成线程块(Block)，若干线程块又组成整体的线程格(Grid)，同一个线程块中的线程可以通过共享存储器以很低的代价进行通信。 CUDA 架构通过将线程块映射到SM 上实现应用程序的并行计算。 SM通过线程调度器实现任务的分配，每个SM 能够运行一个或多个线程块。 根据线程块数目和每个线程块中线程数目的不同，线程调度器能够自动地将一个或多个块分配到SM 上运行。

图1 GPU 结构示意图

2 LOD 裁剪算法原理

当前，LOD 裁剪算法大多基于逐边裁剪思想，构建若干个六面体作为裁剪窗口逐次裁剪实景三维模型中的空间三角形。 裁剪窗口的6 个四边形所在平面将空间划分为27 个子空间，构建6 个裁剪器将裁剪操作分解为裁剪窗口的裁剪面与原始多边形一条边的裁剪。 算法主要思路为:(1) 通过编码值逻辑运算判断三角面空间位置拓扑类型，减少求交计算的数据量；(2) 根据三角面的空间位置进行裁剪。编码值由顶点坐标值与对应边界的差值符号确定，6 位编码值分别表示裁剪包围盒的6 个裁剪面。 如果某编码位的值为1，则代表当前顶点落在了以对应裁剪面划分相对位置的外部，为0 则处于相对位置的内部。 三角面的空间位置拓扑类型由分区编码逻辑运算结果确定。 假设code0、code1、code2 分别表示某三角面的3 个顶点编码，如果3 个顶点编码逻辑“或”计算结果为0，则该面位于裁剪包围盒内；逻辑“与”计算结果不为0，则对应位置为裁剪包围盒外；不满足上述条件的即为相交类型。 单层LOD三维裁剪包围盒如图2 所示。

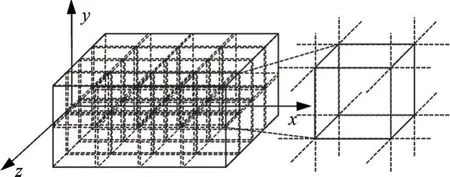
图2 单层LOD 三维裁剪包围盒示意图

判断三角面的空间位置拓扑后，分3 种情况处理:若该面为包含类型，则予以保留；若该面为相离类型，则予以舍弃；若该面为相交类型，则对其进行逐边裁剪求交计算并输出裁剪点序列，三角化后写入裁剪Mesh。 重复上述操作直至遍历所有三角面后裁剪结束，得到裁剪后Mesh 模型。

3 GPU 并行裁剪计算

由LOD 裁剪算法原理可知，CPU 算法以三角面为裁剪元串行裁剪会产生大量的重复编码计算，并且重复计算量会随着Mesh 模型中三角面数量以及复杂度增加，影响算法时间效率。 为适应倾斜摄影三维模型LOD 快速裁剪需求，文章利用GPU 的并行计算能力，优化算法流程，提出了一种基于GPU的实景三维模型裁剪算法。 为了在GPU 上高效地执行裁剪计算，每个线程的负载应该在相同的比例上。 由于非相交类型三角面不参与求交计算，假设算法仅用一个kernel 实现，每个线程中分配一个三角面，会导致活跃线程数减少、GPU 隐藏延迟的能力下降，并且无法解决不必要重复编码计算问题。因此，将裁剪过程分解为:(1) 计算所有顶点分区编码，避免重复编码计算；(2) 对相交类型三角面逐边裁剪计算，设计基于面拓扑的多级索引结构，索引重复交点，实现线程间负载均衡；(3) 对裁剪点序列三角化，编号构建Mesh 拓扑关系。

同时，考虑到kernel 并行特点与Device 内存的限制，设计的适合CUDA 并行的Mesh 存储格式如图3 所示。 GPUVertices、GPUFaces、GPUEdges 分别存储Mesh 的点、面、边信息，包括顶点坐标及编号、面顶点编号、面邻接拓扑、边顶点编号、边所在面编号及局部编号等。

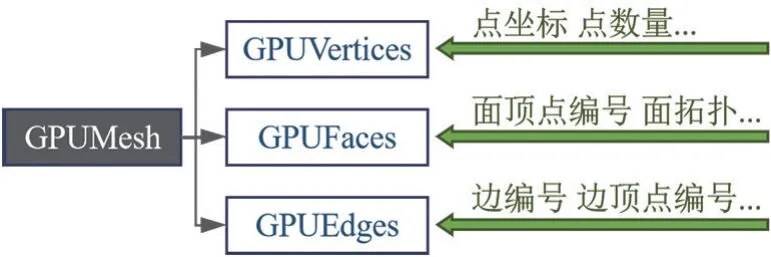
图3 GPUMesh 数据组织图

3.1 空间位置拓扑类型判断

裁剪的第一步是确定三角面的拓扑类型，其由编码逻辑运算确定，以三角面为单位通常更容易求解。 因此，大多数现有的算法将编码计算与拓扑类型判断整体上划分为同一子任务。 但该方法会产生大量点编码的重复计算。 以连接5 个三角面的顶点为例，传统算法需要重复计算该顶点编码5 次，存在着4 次重复计算。 由于编码计算与拓扑判断相互是独立的，因此针对编码计算中重复计算造成的性能损失问题，将任务分解为点编码计算与面拓扑判断两部分。

编码计算kernel 每个线程的主要任务是确定所有顶点的编码。 编码值计算方式由顶点坐标值与对应裁剪边界的差值符号确定，分别判断裁剪包围盒6 个平面，得到对应的6 位编码值。 计算顶点编码后，面拓扑判断kernel 每个线程的主要任务是编码逻辑运算。 在线程中输入三角面，通过逻辑运算确定线程内三角面的空间拓扑类型后结束。

3.2 逐边裁剪

在编码计算确定三角面空间位置拓扑类型后，需处理的三角面数量大大减少。 由逐边裁剪算法原理可知，每个裁剪元的裁剪计算之间相互独立，有着极高的并行性。 在实际应用中，三角面经过裁剪可能包含9 个顶点。 受GPU 并行处理特点限制，若以变长数组存储裁剪多变形顶点，实现复杂且无法保证算法时间效率。 综合考虑内存消耗与该应用程序特点，以最大顶点数分配内存，采用定长数组存储裁剪后顶点编号及坐标，并将新增顶点编号存储为顶点数与该点存储位置之和。 但是，该方法会导致共享交点的多次编号。 重复点索引示例如图4 所示。以0 号面为例，裁剪交点b、c 在3 和1 号面所在线程多次编号。 因此，针对共享交点多次编号产生重复点问题，文章设计了一个基于面拓扑的重复交点索引结构，构建相交类型三角面的拓扑关系以查找重复顶点，并确保每个线程仅处理一个三角面与其相邻面保证线程间负载均衡。

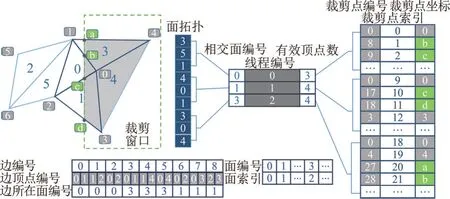
图4 重复点索引示例图

由图4 可以看出，Mesh 中线段最多连接两个三角面，可以通过面拓扑查找对应共享边上的拓扑信息，对于非共享边上的面拓扑信息则表示为该面本身。 裁剪后点编号表示相交类型三角面被裁剪后的多边形点序列，可以根据多边形点序列中有效顶点数查找目标点。 裁剪点坐标与裁剪点编号一一对应，存储新增点的点坐标。 裁剪点索引用于根据面编号查找其所在线程，如由面编号等于3 可以查找到其线程索引为2。 线程内基于面拓扑的索引结构查找过程如图5 所示，根据线程编号可以查询到线程内三角面编号及其面拓扑信息，进而根据面－线程间索引查询到该三角面与其面临域内三角面裁剪点序列，比较坐标后即可定位重复点。

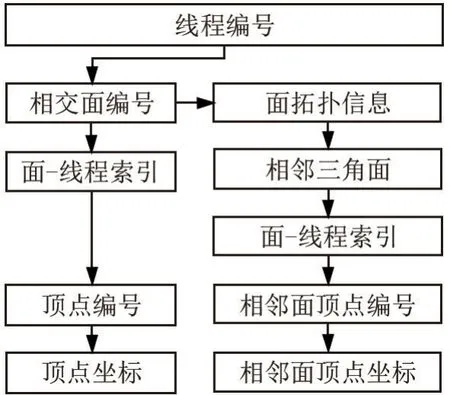
图5 基于面拓扑的索引结构图

索引结构的关键在于面拓扑的构建，根据面拓扑可以从当前相交三角面查找出与该面相交的所有三角面。 主要构建思路为:(1) 将三角面边的顶点编号与所在面编号信息写入GPU；(2) 构建辅助排序数组，根据辅助排序数组中元素值对Mesh 中边排序，排序后使顶点相同的边在数组内相邻；(3) 在线程中索引一组相邻边，比较顶点编号并构建拓扑关系。 其中，辅助排序数组元素为边起点编号乘以MAX＿INT 与终点编号之和。 排序示例如图6 所示。

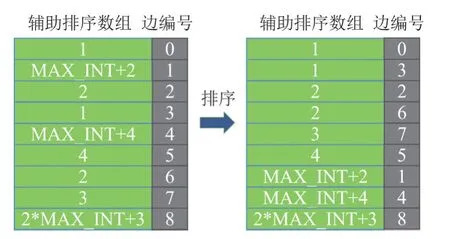
图6 排序示意图

确定每个三角面及其面拓扑后，遍历该面裁剪点序列中顶点与临接面顶点就可以确定重复点。 因此，去重过程中每个线程的主要任务是重复交点测试，测试由几个嵌套循环组成，这意味着有大量的判断分支，因测试的频率较高，分支的减少将带来相当大的性能改进。 因此，考虑到该应用程序的特点，仅对临接面编号小于当前面编号情况进行重复点标记，将当前面该点编号转换为临接面点序列中该点编号，避免线程间读写冲突的同时，消除了测试过程的最大(最外层)分支。

3.3 多边形三角化

Mesh 在裁剪后得到若干组多边形点序列，需要进行三角化以保持Mesh 三角网格结构，同时因逐边裁剪计算相互独立，多边形点序列中存在大量重复交点，需要去重并构建Mesh 拓扑关系，避免裁剪结果出现缝隙、T 形交点等错误[4]。

由几何学的知识可以知道，连接凸多边形的任意两个不相邻顶点，可以将其划分成两个小的凸多边形[15]。 递归执行该步骤直到多边形不能继续划分为止，即可完成该多边形的三角化。

在诸多三角化方法中，最简单的算法就是耳切法。 具体思路是找出n 个顶点简单多边形的一个耳朵来构造一个三角形，并将这个耳朵的耳尖从简单多边形的顶点数组中剔除。 简单多边形的耳朵，是指由连续顶点V0、V1和V2组成的内部不包含其余任意顶点的三角形。 V0与V2之间的连线称之为多边形的对角线，点V1称之为耳尖[16]。 针对由N 个定点组成的多边形，找到其耳尖，移除唯一耳尖上的顶点，此时剩余顶点组成了一个n－1 个顶点的简单多边形[17]。 递归执行上一步直到剩下2 个顶点为止，这样就把这样一个简单多边形构造成了一组三角形。 为提高算法性能，耳切法使用双向链表存储多边形，遍历顶点寻找耳朵。 对于每个顶点Vi和围绕该顶点的三角形＜Vi－1、Vi、Vi＋1＞，测试其余顶点是否在当前三角形中，若有顶点在三角形里面，则不是耳尖[18]。 在实验中可以发现如果一个顶点是耳尖，则一定是凸顶点。 由于三角形被裁剪面裁剪后所有顶点均可视为耳尖，且形成的凸多边形顶点数有限，因此省去原算法中链表构建等过程，进一步简化了三角化算法。 其算法流程图如图7 所示。

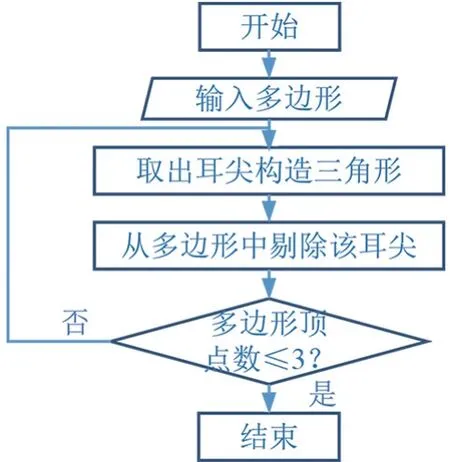
图7 耳切法流程图

针对多边形点序列中的重复交点，算法通过构建计算编码数组前缀和(Prefix sum)的方式构建Mesh 拓扑关系。 主要思路为对原Mesh 与裁剪后新增顶点、三角面编码，需要保留的编码为1，否则编码为0。 计算编码数组前缀和，将所有点、面分配到线程中，获取该点、面的编码判断取舍，获取编码前缀和作为该点、面编号。 编号后将Mesh 下载至CPU 中裁剪结束。 前缀和计算方式如图8 所示，前缀和数组中的元素为编码数组中对应位置前所有元素之和。 前缀和数组对应存储位置即为裁剪结果Mesh 的点、面编号。

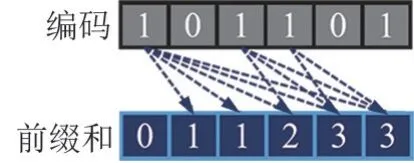
图8 Prefix sum 示意图

3.4 算法性能优化

为进一步提升基于GPU 的三维模型裁剪算法性能，在现有算法的基础上进行优化，以保证算法的并行效率。

(1) 快速浮点计算 在处理裁剪窗口与三角形的交点问题时，精度问题显得尤为重要。 如果使用浮点运算，由于精度不高，可能会产生误差导致裁剪结果出现裂缝等拓扑错误。 相反，精确的算法可以修复这些错误，但会导致较低的性能。 为了解决点三角化时的精确性问题，文献[19]采用了两道计算策略，即①通过浮点运算处理所有数据，并标记需要精确计算的数据；②计算采用多精度算法，并且只对标记的数据执行。 精确的运算是通过增加数字的位数实现的，因此需要更多的硬件资源如寄存器和缓存，这会导致算法并发性较低。 与混合方法不同，文章通过调整线段的方向实现了基于浮点精度的高精度计算，从而实现了更高的性能。 在交点计算中，应计算线段顶点坐标差值分量的绝对值及差值符号，再根据绝对值最大分量的差值符号限制线段起点。 若差值符号为负号，则交换起点与终点；否则，保持现有关系。 该方法确保了相同线段交点计算的浮点计算误差相同，满足裁剪精度要求。

(2) 空间排序 当相邻线程访问内存的相邻位置的时候，算法能获得内存的最佳带宽，通过沿着空间填充曲线对点、三角面等数组排序，可以改善裁剪时的随机内存访问。 以同样的方式，去重复点和Mesh 重构也受益于空间排序。

(3) 线程分配 对于Block 维度的设定，一个合适的Block 维数可以使得并行问题更好地映射到CUDA 架构上，但对程序运行效率起的作用很小[20]。 同时，GPU 中的多流处理器(SM)在取指令和发射指令时，是以warp 为单位并交给流处理单元(SP)执行的。 因此，为了有效利用执行SP，线程分配不考虑Block 维度，每个Block 中线程数目均设置为线程数(32)的倍数[21]。

4 实验结果与分析

4.1 实验环境与实验数据

实验平台的CPU 为Intel Core i7－6700，其主频为3.40 GHz、内存为16 GB，GPU 为Nvidia GeForce GTX 1050，GPU 主要配置参数见表1。 所有程序在Windows10 系统下的Visual Studio 2017 和CUDA10.1环境下运行。 CPU 上的对比版本由VCGLib 框架提供。

表1 GPU 设备参数表

为测试算法的性能，选取9 组不同大小的基于倾斜影像构建的实景三维Mesh 模型数据进行实验测试。 所有影像数据均采用搭载DQ5 倾斜摄影测量系统的多旋翼无人机获取影像，Mesh 模型数据均采用ContextCapture 软件获得实景三维建模。 影像采集区域分别位于湖北省武汉市、河北省石家庄市、广东省东莞市、福建省福州市。 Mesh 模型信息表见表2。

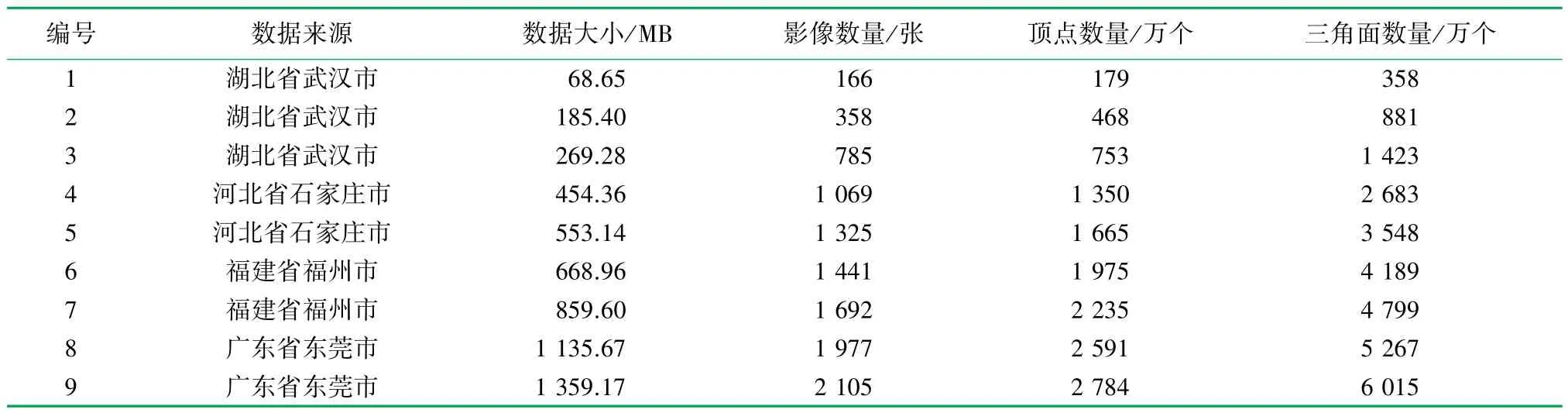
表2 Mesh 模型信息表

4.2 结果分析

为了比较不同数据量对处理效率的影响，设计3 组实验以验证算法性能，其中第一组实验运行基于CPU 平台的串行裁剪算法；第二组实验运行GPU平台的并行裁剪算法；第三组实验运行性能优化后的GPU 平台并行裁剪算法。 针对多组测试数据，多次测试取其平均统计值进行分析，计算出各组实验的平均耗时，数值结果保留小数点后两位。 定义加速比s 为串行算法执行时间和并行算法执行时间之比，由式(1)表示为

式中TS、Tp分别为串行算法、并行算法的执行时间，ms。

加速比反映了在相应并行计算架构下的并行算法相比于CPU 串行算法系统执行效率的改善情况，能够对实际系统的速度客观评价。 不同Mesh 数据的并行裁剪结果如图9 所示，其中图9(a)～(c)为高楼和古建筑等区域，图9(d)～(f)为住宅和道路，图9(g)～(i)为田地区域。 所有区域均取得了正确裁剪结果，保证了CPU 算法性能。

图9 不同Mesh 数据的并行裁剪结果

在单次裁剪实验中，算法执行时间对比见表3，当Mesh 数据大小相同时，GPU 并行算法相对CPU串行执行时间都有不同程度的缩减，即均获得了加速效果。 对于数据大小为68.65 MB 的1 号数据，Mesh 串行裁剪运算时间为549.63 ms，在CUDA 计算平台下运算时间大幅缩短为159.77 ms，性能优化后则进一步缩减为150.58 ms。 在相同大小数据下，并行处理后的裁剪算法的运算时间相比单线程的串行算法运算时间有明显的减少，并且在相同的线程数下随着Mesh 数据规模的增大，其运行时间也越来越长，基本符合线性增长的趋势。

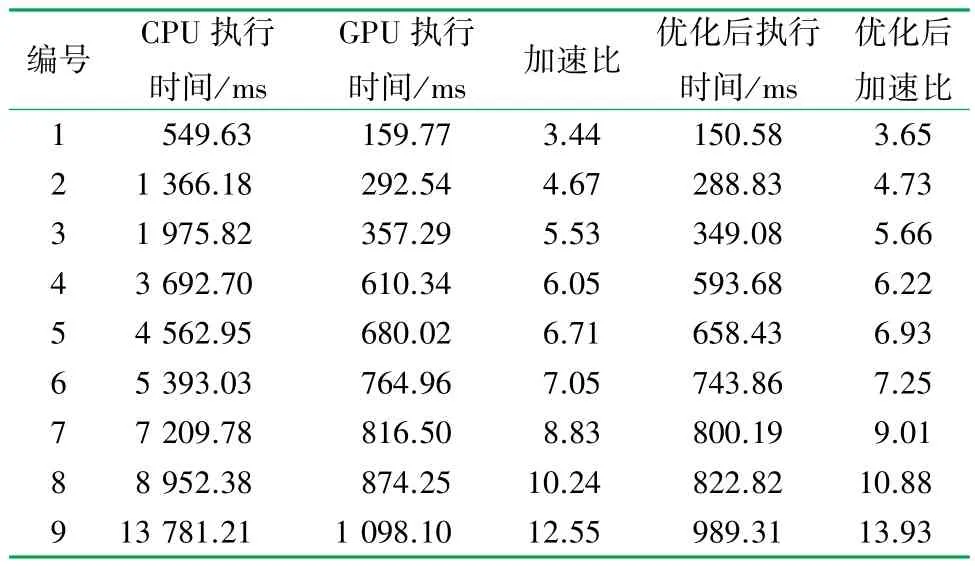
表3 单次裁剪中CPU 与GPU 算法的执行时间表

Mesh 数据大小与加速比关系如图10 所示，并行裁剪算法的加速比随着Mesh 数据增大而增大，主要原因是当Mesh 数据较小时，GPU 算法大部分时间消耗在系统调度方面，设备高性能计算的优势没有展现，单次裁剪运算时间与CPU 运算时间差别不明显；随着数据的增大，GPU 算法在编码计算等计算密集型任务中的性能充分发挥，加速比也随之上升。

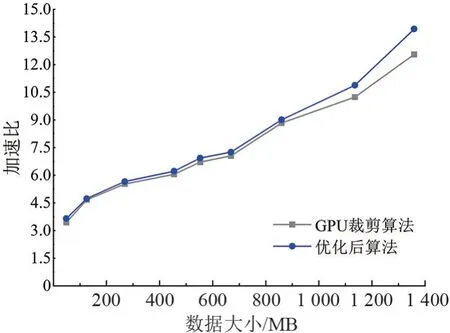
图10 Mesh 数据大小与加速比关系图

在单层LOD 裁剪实验中，算法执行时间见表4。可以看出，在相同数据下单层裁剪加速比要比单次裁剪加速比高得多，主要原因是CPU 裁剪算法逐面进行串行处理，随着实验的裁剪次数增加，裁剪耗时呈线性增加。 而使用GPU 裁剪算法多次裁剪的情况下，CPU 和GPU 间的数据传输与单次裁剪一样只需要上传和下载两次，避免了CPU 和GPU 间频繁的数据传输，减少了数据传输造成的耗时占比，加速比也随之增长。 为测试文章算法最大性能，对9 组数据进行固定裁减次数的多组实验，裁剪次数与加速比的关系如图11 所示。 随着裁减次数增加，加速比增长速度也随之增加。 不管是在给定递增裁剪次数的模式下，还是给定足够多的裁剪次数的模式下，相比于CPU 串行裁剪算法，所提出的GPU 并行算法都可获得约10 倍以上的加速。

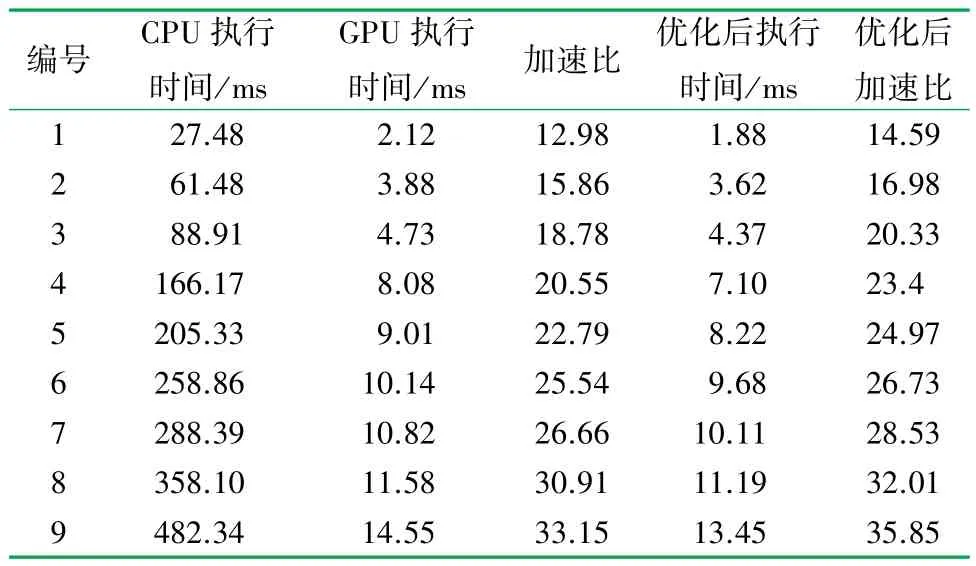
表4 LOD 多次裁剪中CPU 与GPU 算法的执行时间表

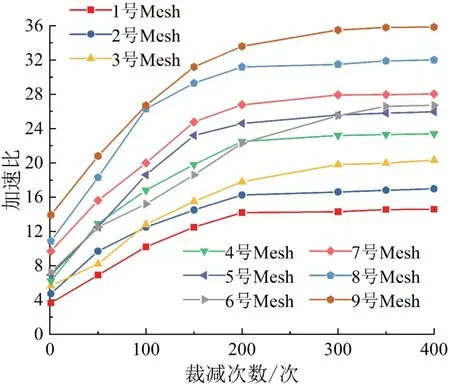
图11 裁剪次数与加速比关系图

同时，为测试文章所采取的优化策略对于提升三维模型裁剪并行算法性能的有效性，对比采取优化策略与未采取优化策略的实验结果，结果如图12所示。 可以看出，以优化前算法(未采取优化策略)加速比1 为基准，文章的3 种优化策略在不同数据下均获得了不同程度的性能提升，其中空间排序与线程分配优化策略对算法3 个部分都有影响，因此加速效果较为明显。 快速浮点计算仅用于算法的裁剪部分，但也在一定程度上提高了算法的性能。

图12 优化策略加速比对比结果图

5 结论

针对当前倾斜摄影实景三维模型的常用裁剪算法存在的时间复杂高、计算效率较低等问题，文章提出了一种基于GPU 的实景三维模型裁剪算法。 在保证裁剪结果准确的情况下，最大限度地利用了GPU 并行计算资源，提高算法效率。 通过多次试验测试性能后，得到以下结论:

(1) GPU 并行算法相较于传统CPU 算法，在保证CPU 算法性能的前提下，单次裁剪实验中最大获得了13.93 倍的加速比，在LOD 构建实验中加速比达到了35.85，并且在所有实验数据集中都有不同程度的优化，均获得了加速效果。

(2) 在相同的实验条件下，随着Mesh 规模的增大，GPU 算法在编码计算等计算密集型任务中性能充分发挥，加速比也随之上升。

(3) 由于LOD 多次裁剪情况下，主机与设备间数据传输造成的耗时占比下降，因此随着裁剪次数增多，加速比随之增大。

(4) 为了更好地发挥GPU 性能，需要通过对算法的深入剖析，尽可能优化数据的存储；通过CPU与GPU 协同计算的方式，减少GPU 内存消耗；研究多GPU 协同计算机制，并利用GPU 集群进一步提升算法的性能。