闭环供应链中制造商以旧换新渠道决策

唐 飞,代 颖,马祖军,3

(1.西南交通大学 经济管理学院,成都 610031;2.重庆工商大学 工商管理学院,重庆 400067;3.服务科学与创新四川省重点实验室,成都 610031)

随着经济的发展和竞争的加剧,许多企业都在采用各种促销手段来刺激消费、促进新产品的销售,其中以旧换新作为一种常见的促销方式在家电、消费电子、汽车等行业有广泛应用[1-2]。由于消费者通过以旧换新购买新产品可以获得一定的价格折扣,而企业提供以旧换新可以回收消费者手中的旧产品进行再利用,这使得以旧换新不仅能够促进新产品销售,而且能够促进废旧产品回收再利用[3]。例如:苹果公司推出的手机以旧换新服务给消费者提供一种礼品卡用于购买新产品,并将回收的旧产品通过不同方式进行再利用;华为、联想、IBM、Canon等也提供了类似的以旧换新服务[3-4]。除了制造商提供以旧换新服务之外,一些零售商也会提供以旧换新服务,例如,拥有旧Kindle的客户可通过Amazon的以旧换新服务获得购买新产品的折扣,京东、苏宁等大型零售商也推出了支持各种家电、手机和电脑设备进行以旧换新的促销活动[4-5]。可见,制造商可以自主提供以旧换新服务,也可以让零售商提供以旧换新服务。

目前有关以旧换新问题的研究主要集中在企业的以旧换新策略以及如何确定最优定价和以旧换新折扣等方面。

就企业的以旧换新策略而言,Li等[6]研究了二级市场存在与否对OEM 定价和以旧换新决策的影响,指出OEM 希望拥有旧产品的消费者都参与以旧换新且回收的旧产品都能进行再制造并销售到二级市场。Feng等[7]进一步研究了无以旧换新、存在以旧换新但无二级市场和以旧换新与二级市场同时存在3种情形对企业定价和产品质量的影响,结果表明:当只有以旧换新时,企业会降低产品质量;当以旧换新和二级市场同时存在时,企业会提升产品质量。Liu等[8]通过建立两周期以旧换新模型,分析了产品更新换代下策略消费者对以旧换新策略的影响,发现当旧产品残值较高时,第二周期仍然可以销售上一代产品。Cao等[9]以京东等B2C 平台为研究对象,在自营店和他营店存在竞争的背景下,研究了礼品卡和现金券这两种以旧换新策略对平台利润的影响。Li等[10]对网络回收平台的以旧换现、以旧换现/翻新和以旧换现/翻新/新3种策略进行了研究,发现回收平台应根据旧产品质量和新产品价值确定采用何种策略。Zhu等[11]将以旧换新问题扩展到两竞争性企业,研究了企业面临竞争时是否应当提供以旧换新服务,指出以旧换新服务有助于增强企业的竞争优势。刘靓晨等[12]进一步研究了产品更新换代对竞争型企业以旧换新策略的影响。石平等[13]在市场存在非正规回收企业竞争情形下,对厂商是否自主提供以旧换新进行分析,发现厂商自主以旧换新可以提升其与非正规回收企业竞争的优势。

在以旧换新定价研究方面,Ray等[14]研究了3种以旧换新定价策略(统一定价、与使用时间无关的差别定价和基于使用时间的差别定价),指出最优以旧换新定价策略主要受产品耐用度和新老顾客市场份额等参数的影响。Xiao等[15]提出了一种半动态以旧换新定价方案,即针对初始消费者采用静态定价,对再次消费者采用动态定价。罗子灿等[16]从产品设计角度,研究了以旧换新服务对产品一体化架构和模块化架构下最优定价的影响,指出当下一代产品质量较高时,模块化架构对企业更有利。此外,也有一些文献从供应链角度探讨了以旧换新的最优定价与折扣问题。Miao等[17]研究了制造商以旧换新、制造商委托零售商以旧换新和一体化以旧换新3种供应链模型,发现制造商提供以旧换新对自身最有利,而一体化以旧换新下供应链利润最高。缪朝炜等[18]研究了第三方回收商负责以旧换新时对闭环供应链定价决策的影响。颜波等[19]针对由制造商和零售商组成的供应链,研究了零售商自主以旧换新的定价策略,发现该策略受产品成本、旧产品折旧度等因素的影响。易余胤等[20]对汽车供应链以旧换新燃油车和以旧换新能源车两种策略下的最优定价进行了研究,得到了不同条件下的最优定价策略。上述研究从供应链视角研究了以旧换新对产品定价决策的影响,但未考虑应当由制造商还是零售商提供以旧换新的问题。为此,李鸿媛等[21]探讨了制造商提供以旧换新和零售商提供以旧换新对双方利润的影响。Xiao[22]假设零售价和批发价均为外生,研究了二级市场的存在对制造商或零售商提供以旧换新的影响,发现制造商和零售商都希望“搭便车”,让对方提供以旧换新。

上述关于以旧换新的文献都忽略了以旧换新固定成本(以下简称固定成本)对企业以旧换新决策的影响。但实际上,提供以旧换新服务需要投资建立相应的回收系统,旧产品回收、堆放、运输、处理等都需要支出费用,而且对以旧换新活动进行广告促销宣传也要付出成本,综合起来的成本就不可忽略[23]。Cho等[24]和Ha等[25]将促销产生的广告、运营等费用整体视为企业的一种固定成本投入,研究发现,该成本对企业是否提供促销活动有重要影响。Yenipazarli[26]和Raz等[27]则将建立废旧产品回收系统所支出的费用视为企业参与回收活动的固定成本,并指出该成本太高会使企业放弃回收废旧产品。类似地,企业提供以旧换新服务所产生的促销和回收这两方面成本也应视为固定成本,并将影响企业的以旧换新决策。鉴于此,本文区别于已有与以旧换新相关的研究[3-22],考虑当闭环供应链中的制造商或零售商提供以旧换新服务时,一方面要承担相应的固定成本,另一方面也会因以旧换新促进销售和获得旧产品而增加收益,由此需要对提供以旧换新服务产生的成本和收益进行权衡,以确定是否应该提供以旧换新服务。此外,本文在制造商或零售商提供以旧换新服务的情形下,设计了相应的以旧换新补偿和协调机制,对闭环供应链利润进行再分配,以确保双方都能从以旧换新中受益,这也是本文与上述研究的不同之处。

综上所述,本文考虑由制造商和零售商构成的闭环供应链,双方都可能提供以旧换新服务并承担相应的固定成本,着重研究闭环供应链中制造商应该自主提供以旧换新服务还是让零售商提供以旧换新服务的问题。通过分别构建无以旧换新服务、制造商提供以旧换新服务和零售商提供以旧换新服务3种闭环供应链以旧换新模型,分析固定成本变化对闭环供应链成员以旧换新决策的影响,并针对制造商和零售商在提供以旧换新方面可能存在冲突或“搭便车”现象,进一步考虑制造商如何设计适当的补偿或协调机制来引导以旧换新获利方对受损方进行补偿,以实现闭环供应链协调。

1 问题描述与需求分析

1.1 问题描述

考虑由一家制造商和一家零售商构成的闭环供应链,制造商以单位成本c生产新产品,并以批发价w卖给零售商,零售商再以价格p销售给消费者。市场中存在两类消费者,即尚未购买该产品的初始消费者和已经拥有旧产品的再次消费者。假设市场规模标准化为1,其中,再次消费者的比例为α(0＜α＜1),初始消费者的比例为(1-α)[15,19,21]。

制造商在进行新产品销售的同时也在考虑是否应该自主向再次消费者提供以旧换新服务或让零售商提供以旧换新服务,以促进新产品销售和废旧产品回收再利用。在实践中,通常有3 种情形(见图1):①制造商和零售商(如Ben Q、飞利浦)都不提供以旧换新服务(模型N);②制造商(如IBM、Canon、联想)提供以旧换新服务(模型M);③零售商(如Amazon、苏宁)提供以旧换新服务(模型R)。当制造商或零售商提供以旧换新服务时,通常会产生两类成本:①由以旧换新广告、运营、建立回收系统等产生的以旧换新投资F i(i=M,R),可视为提供以旧换新的固定成本;②以旧换新提供者给再次消费者的以旧换新折扣r,可视为提供以旧换新的单位变动成本。此外,通过以旧换新服务回收的旧产品仍具有一定残值,可为以旧换新提供者带来一定的收益,设单位旧产品的收益为s[3-6]。在此背景下,制造商和零售商需要权衡提供以旧换新服务的成本和收益,以确定是否提供以旧换新服务,以及由谁来提供会更好。

图1 闭环供应链以旧换新决策模型Fig.1 The trade-in decision models of closed-loop supply chains

1.2 需求分析

假设初始消费者和再次消费者对新产品的价值评价均为v,且服从[0,1]的均匀分布[3-9]。再次消费者对旧产品的价值评价为θv,其中θ(0＜θ＜1)为该产品的耐用度,其大小反映了旧产品的剩余价值[3,6-7]。初始消费者购买新产品的效用为μn=vp。对于再次消费者,当无企业提供以旧换新服务时,其直接购买新产品的效用为μr=v-p;当制造商或零售商提供以旧换新服务时,其通过参与以旧换新活动购买新产品的效用为μt=v-p+r;若再次消费者选择继续使用旧产品,其效用为μo=θv。则当μn＞0时,初始消费者会选择购买新产品,相应的需求为

对于再次消费者,如果制造商或零售商都不提供以旧换新服务,则当μr＞0且μr＞μo时,再次消费者才会购买新产品,相应的需求为

如果制造商或零售商提供了以旧换新服务,再次消费者会通过参与以旧换新活动购买新产品,因为这样可以获得相应的折扣[11-12,14]。因此,当μt＞0且μt＞μo时,再次消费者会选择通过参与以旧换新活动购买新产品,相应的需求为

2 闭环供应链以旧换新决策模型

假设制造商和零售商之间进行Stackelberg博弈,制造商为主导方,零售商为跟从方,双方都以追求自身利润最优化为目标进行决策[17,21-22,28]。用表示供应链成员i在模型j下的利润,则该供应链系统利润为其中,i=M,R,j=N,M,R。下面分别对无以旧换新服务、制造商提供以旧换新服务和零售商提供以旧换新服务3种情形下的闭环供应链定价决策进行建模和求解。

2.1 模型N:无以旧换新服务

模型N 用作比较基准。此时,制造商先决策批发价w,零售商再决策零售价p。制造商和零售商的利润函数分别为:

通过逆向归纳法可以求得该模型下的最优定价及利润,如表1所示(证明见附录)。

表1 3种闭环供应链决策模型的最优结果Tab.1 The optimal outcomes of three closed-loop supply chain decision models

2.2 模型M:制造商提供以旧换新服务

当制造商提供以旧换新服务时,其需要承担相应的固定成本FM。制造商不仅要决策批发价w,还要决策给予再次消费者的以旧换新折扣r,在此基础上,零售商决策相应的零售价p。此时,制造商和零售商的利润函数分别为:

类似地,通过逆向归纳法可以求得该模型下的最优定价及利润(见表1)。

2.3 模型R:零售商提供以旧换新服务

当零售商提供以旧换新服务时,其需要承担相应的固定成本FR。制造商先决策批发价w,在此基础上,零售商决策相应的零售价p和以旧换新折扣r。此时,制造商和零售商的利润函数分别为:

该模型的最优定价及利润见表1。由表1可以得到如下推论。

推论1为保证上述模型有意义,需满足如下条件:①3种模型下的需求都大于0;②当制造商提供以旧换新服务,其利润不低于无以旧换新服务下的利润时,才有动力提供以旧换新服务;③当零售商提供以旧换新服务时,其利润也应当不低于无以旧换新服务下的利润。由此可得3种模型的存在条件,如表2所示。

表2 3种闭环供应链决策模型的存在条件Tab.2 The existence conditions of three closed-loop supply chain decision models

推论1表明:

(1) 无以旧换新服务下,只有当生产成本足够低时,初始消费者才会购买新产品,这是因为制造商的生产成本直接影响批发价,进而间接影响零售价。显然,生产成本越低,越能吸引初始消费者购买新产品。对于再次消费者而言,其会比较购买新产品的效用与继续使用旧产品的效用,只有当产品耐用度足够低,再次消费者继续使用旧产品的效用更低时,才会放弃使用旧产品转而购买新产品。当产品耐用度θ→0时,再次消费者的购买选择与初始消费者趋同。

(2) 只有当固定成本足够低时,制造商或零售商才愿意提供以旧换新服务,即通过以旧换新促进新产品销售和废旧产品回收带来的收益大于提供以旧换新的固定成本时,制造商或零售商提供以旧换新服务才有利可图。此外,产品生产成本提高、旧产品残值降低或固定成本增加,都可能导致制造商或零售商放弃提供以旧换新服务。与模型N 类似,在模型M 和R 下,当生产成本足够低时,初始消费者才愿意购买新产品;当产品耐用度足够低时,再次消费者才愿意参与以旧换新活动。由于模型M 和R的最优零售价与以旧换新折扣都相同,故初始消费者和再次消费者购买新产品的条件也完全一致。

(3) 对制造商或零售商愿意提供以旧换新服务的条件(T1和T2)进行比较,可以发现,

这说明,制造商提供以旧换新服务的条件比零售商提供以旧换新服务的条件更宽松,制造商能够承受更高的固定成本。

下面通过比较上述3种供应链决策模型的最优结果,分析不同情形下以旧换新服务提供者的均衡结果。值得一提的是,由推论1和表2可知,为了保证上述3种供应链决策模型都有意义且可比较,产品生产成本需满足c＜min{c1,c2},产品耐用度需满足θ＜min{θ1,θ2}。

3 以旧换新服务提供者的均衡分析

由表1可知,零售价和以旧换新折扣在两种以旧换新模型下都相同,两种模型下产生的收益也相同,但制造商会通过批发价的变化来影响供应链系统利润在内部的分配。此外,由于两种模型下的定价和以旧换新折扣相同,再次消费者并不关心由谁提供以旧换新服务的问题,但制造商和零售商却需要比较实施以旧换新增加的利润和支出的成本,以确定是否提供以旧换新服务。

当企业提供以旧换新服务需要承担一定的固定成本时,制造商和零售商会权衡自己提供以旧换新服务或对方提供以旧换新服务对自身利润的影响,由此可得推论2。

推论2

(1) 当FM≤T3时,制造商希望自己提供以旧换新服务。

(2) 当FR≤T3时,零售商希望自己提供以旧换新服务。其中

由推论2可知,制造商和零售商愿意自己提供以旧换新服务的条件都是相应的固定成本不超过T3。因此,当两企业提供以旧换新服务的固定成本都低于T3时,双方都希望自己提供以旧换新服务,从而会产生冲突。另外,由

和T1＞T2可知,固定成本临界值T1、T2和T3之间有T1＞T2＞T3。据此,可以进一步分析当两企业的固定成本处于不同区间时如何影响以旧换新提供者的均衡结果,如命题1所示。

命题1当制造商和零售商提供以旧换新服务的固定成本F i(i=M,R)处于不同区域时(见图2),以旧换新服务提供者的均衡结果有所不同(见表3)。具体如下:①在区域A1,模型M 和R 都是均衡结果,即制造商和零售商都希望提供以旧换新服务,这将导致冲突;②在区域A2、A3和A4,模型R 是唯一均衡结果;③在区域A5,模型M 和R都是均衡结果,即制造商和零售商都希望由对方提供以旧换新服务,即双方陷入“囚徒困境”;④在区域A6、A7和A8,模型M 是唯一均衡结果;⑤在区域A9,模型N 是唯一均衡结果。

表3 不同固定成本范围下以旧换新服务提供者的均衡结果Tab.3 The equilibrium outcomes of trade-in service providers under different fixed cost ranges

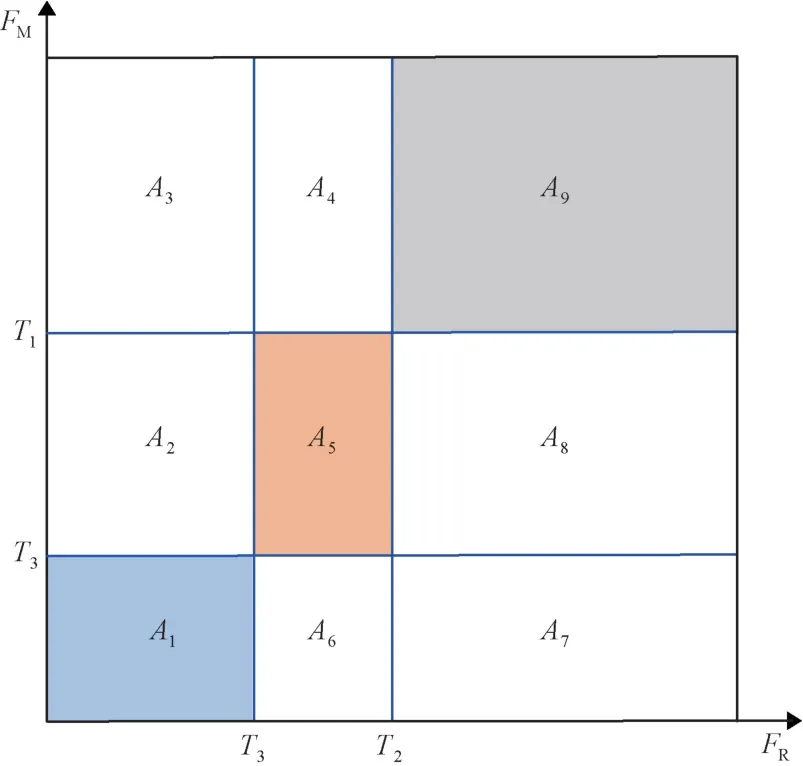
图2 固定成本区域的划分Fig.2 The classification of fixed cost regions

命题1指明了在何种情形下制造商应该自主提供以旧换新服务或让零售商提供以旧换新服务。具体而言,当固定成本位于区域A1时,模型M 能给制造商带来更大利润,而模型R 能给零售商带来更大利润,此时双方陷入冲突,这是因为双方都具有成本优势而希望自己成为以旧换新服务的提供者。当零售商提供以旧换新服务的固定成本低于T3,而制造商提供以旧换新服务的固定成本超过T3时(即区域A2、A3),模型R 是唯一均衡结果,并且使得制造商和零售商的利润都能达到最优;当T3＜FR＜T2且FM≥T1时(即区域A4),虽然零售商提供以旧换新服务对其而言是次优的,但制造商完全不具备提供以旧换新服务的成本优势,故模型R 仍然是唯一均衡结果。类似地,若制造商提供以旧换新服务的固定成本低于T3,而零售商提供以旧换新服务的固定成本超过T3时(即区域A6、A7),制造商提供以旧换新服务对双方都是最优的,故模型M 是唯一均衡结果;当T3＜FM＜T1且FR≥T2时(即区域A8),模型M 是唯一均衡结果,这是因为此时制造商提供以旧换新服务对其虽然是次优的,但零售商由于成本劣势始终不可能提供以旧换新服务。

当制造商和零售商提供以旧换新服务的固定成本都位于中等水平时(即T3＜FM＜T1且T3＜FR＜T2,对应区域A5),虽然制造商或零售商提供以旧换新服务都比不提供以旧换新服务更好,但双方都更希望由对方提供以旧换新服务,通过“搭便车”获取比自己提供以旧换新服务更大的利润,此时双方陷入“囚徒困境”。在这种情况下,因“搭便车”受益的一方可以考虑补偿另一方以激励对方提供以旧换新服务,因为此时两种以旧换新模型下的系统利润都比无以旧换新时的系统利润更高,即πj*＞πN*,其中j∈{M,R};当FM＞T1且FR＞T2时(即区域A9),制造商和零售商都会因为过高的固定成本而放弃提供以旧换新服务。

推论3当FM=FR=F时,有:①当F＜T2时,模型M 和R 都是均衡结果;②当T2≤F≤T1时,模型M 是唯一均衡结果;③当F＞T1时,模型N 是唯一均衡结果。

推论3表明,当制造商和零售商提供以旧换新服务的固定成本相同且都较低时,双方仍然会陷入冲突;当该成本增加到一定程度(T2≤F≤T1)时,只有制造商具有提供以旧换新服务的成本优势,而零售商由于成本劣势会放弃提供以旧换新服务;当该成本足够大(F＞T1)时,双方都会放弃提供以旧换新服务。

为了更直观地了解固定成本F和旧产品残值s变化对均衡结果的影响,借鉴Cao等[3]的参数取值,令α=0.4,c=0.2,θ=0.3,结果如图3所示。

图3 参数s 和F 对均衡结果的影响Fig.3 The effects of parameters s and F on equilibrium outcomes

由图3可知,即使旧产品残值s=0,在固定成本较低情形下,以旧换新模型M 和R 仍然可能是均衡结果,并且随着s的不断增加,两种以旧换新模型可以承受的固定成本也不断增加,即均衡结果为模型M 和R 的区域不断扩大。因此,建议提供以旧换新服务的企业应当利用多种方式(如拆解处理、再制造或翻新后再售到二级市场)处理旧产品以最大程度地获取其剩余价值,从而扩大实施以旧换新的优势。在实践中,像Apple不仅研发了自动拆解的机器人Daisy来提高拆解效率和再利用率,同时也对质量较好的旧产品进行翻新处理后销售到二级市场,以获得更高收益[5-6]。这一做法显然是为了最大程度地获得旧产品的剩余价值,这也值得其他以旧换新提供者借鉴学习。

综合命题1和推论3的结论,可以看出,固定成本的大小对以旧换新服务提供者的最优选择有重要影响。相关结论可以解释现实中为何既存在像Ben Q 和飞利浦这样未提供以旧换新服务的企业,也存在由制造商(如IBM、Canon、联想)或零售商(如Amazon、苏宁)提供以旧换新服务的情况,这主要是因为他们提供以旧换新服务的成本不同。因此,建议制造商和零售商应充分衡量提供以旧换新服务的成本和收益,以确定最佳的以旧换新服务提供者。此外,本文所得结论不仅验证了Xiao[22]关于供应链成员可能因为都想让对方提供以旧换新服务而产生“搭便车”现象,而且还发现双方也可能因为都想提供以旧换新服务而产生冲突。这一冲突现象也可以解释为何Apple作为制造商而京东作为零售商都在对iPhone手机提供以旧换新服务。

鉴于以往有关以旧换新问题的研究基本忽略了以旧换新的固定成本[3-22],在此也同样分析固定成本为零的特例,以作对比。可以发现,对制造商和零售商而言,都是自己提供以旧换新服务时对自己最有利,双方都不提供以旧换新服务时最不利。即双方都希望自己提供以旧换新服务,此时也将陷入冲突,但与不提供以旧换新服务相比,不管由谁(制造商或零售商)提供以旧换新服务,都能提高自己的利润。因此,当固定成本忽略不计时,不管谁提供以旧换新服务,都能使供应链成员获得比无以旧换新服务时更高的收益,这一结论可以解释为何现实中各行各业(如家用电器、电子产品、汽车、时尚服装等)都存在各种各样的以旧换新促销活动[3,6]。

4 以旧换新补偿与协调机制设计

本节主要基于第3节的研究结果,探讨如何设计以旧换新补偿与协调机制,以确保制造商和零售商都能从以旧换新中受益。具体地,4.1节主要在分散决策下探讨以旧换新受益方是否可以通过补偿另一方来消除以旧换新冲突或“搭便车”现象,从而确保双方利润都比无以旧换新情形更高;4.2节则进一步针对以旧换新分散决策存在的双重边际化问题,探讨如何设计适当的协调机制消除这一问题,从而进一步提升制造商和零售商的利润。

4.1 以旧换新补偿机制

上文研究表明,虽然制造商和零售商之间可能会因固定成本的影响而导致双方在是否提供以旧换新服务方面产生冲突或“搭便车”现象,但从整个闭环供应链系统的利润来看,无论由谁提供以旧换新服务,当固定成本较低时,系统利润都比无以旧换新服务时更高。那么,对于制造商和零售商而言,可否通过受益方给另一方适当补偿来消除这种以旧换新冲突或“搭便车”现象? 为此,下面通过设计合理的补偿方案来解决这一问题,具体见命题2。

命题2当制造商和零售商之间出现以旧换新冲突或“搭便车”现象时,若通过以旧换新受益方给另一方提供适当的补偿来解决,则不同固定成本区域(见图4)下的均衡结果、补偿提供方、补偿条件和补偿额如表4所示。

行业发展有起伏。从2014年开始，在苗木行情的低迷期，农场提出“用苗木生长的时间换取市场增长的空间”，利用国有林地资源优势进行低成本扩张，大力压缩意杨面积，加速推进特色苗木基地建设。短短几年，农场苗圃规模达2000亩40万余株。

表4 存在补偿时以旧换新服务提供者的均衡结果Tab.4 The equilibrium outcomes of trade-in service providers with compensation

图4 存在补偿时固定成本区域的细分Fig.4 The classification of fixed cost regions with compensation

命题2表明,采用补偿时以旧换新服务提供者的均衡结果受两企业固定成本FM和FR的影响。在不同成本区域中,通过制造商给予零售商补偿或零售商给予制造商补偿,均衡区域会细分为更小的子区域,各子区域对应着应该由谁来补偿另一方以及相应的补偿额。

具体而言,对于存在以旧换新冲突的A1区域,制造商和零售商都想提供以旧换新,因而双方都可以作为补偿提供方给予对方补偿以促使其放弃提供以旧换新,从而消除冲突。对于存在“搭便车”现象的A5区域,制造商和零售商都可以通过补偿对方以鼓励其提供以旧换新。对于区域A4,虽然此时零售商有动力提供以旧换新,但制造商仍可以考虑补偿零售商,因为由零售商提供以旧换新会使制造商获利更大。如果零售商不愿提供以旧换新,它也可以考虑补偿制造商,让制造商提供以旧换新。与区域A4相对应的区域A8,若由制造商提供以旧换新,零售商可以对其进行补偿;反之,则制造商也可以通过补偿零售商让其提供以旧换新。值得注意的是,在区域A9,虽然双方都不愿提供以旧换新,但也存在一些子区域(A90、A91、A92)使得提供以旧换新时的系统利润比无以旧换新时的系统利润更高。因此,仍可以通过补偿方案来促使制造商或零售商提供以旧换新,以实现双方利润的改善。而在子区域A93,由于过高的固定成本使得提供以旧换新时的系统利润低于无以旧换新时的系统利润,故此时的最优决策为双方都不提供以旧换新服务。

由表4 还可以发现,对于有些子区域(A41、A80、A90),制造商和零售商都可以作为补偿提供方,此时以旧换新提供者和补偿提供方可以通过双方协商确定。对于由零售商提供以旧换新服务的区域A2和A3,以及由制造商提供以旧换新服务的区域A6和A7,由于双方利润均已达到最优,故无需采用任何补偿方式。

命题2的结论可用来指导供应链成员选择合适的以旧换新服务提供者和补偿提供方以改善双方的利润,具体的补偿额SM或SR可由双方协商确定。值得一提的是,就两种以旧换新模型而言,虽然供应链成员之间通过补偿方式进行利润的再分配可以实现双方利润都比无以旧换新时的利润更高,但由于此时为分散决策,不可避免地会产生双重边际化效应,闭环供应链系统总利润仍未达到最优。那么,是否可以通过契约协调机制来提高整个闭环供应链的利润,同时实现供应链各成员利润的进一步提升? 为此,下面从闭环供应链整体角度对两种以旧换新模型下系统利润的改进做进一步探讨。

4.2 以旧换新契约协调机制

在此考虑闭环供应链集中决策模型(模型C),即将制造商和零售商视为一个整体,以闭环供应链系统总利润最大化为目标决策零售价和以旧换新折扣,同时承担相应的固定成本FM/R。供应链系统利润可表示为

由此可得推论5。

推论5

(1) 当FM/R≤TS时,集中决策能够增加闭环供应链系统利润。

(2) 闭环供应链系统利润有πC*＞πj*,其中j∈{M,R},

容易验证TS＞{T1,T2}。这说明,从闭环供应链整体角度看,集中决策可以承受比分散决策更高的固定成本,克服双重边际化效应,因此,制造商和零售商可以通过协调以达到集中决策的绩效,从而提高各自的利润。研究发现,制造商可以通过降低批发价来促使零售价达到与集中决策时一致,从而实现系统利润最大化。为了弥补制造商因为降低批发价造成的损失,零售商可以从自身增加的利润中分享一部分给制造商,从而保证双方利润都得到提升。命题3 给出了两种以旧换新模型下的协调契约。

命题3

由命题3可知,尽管不同以旧换新模型下的闭环供应链协调契约参数取值有所不同,但无论是由制造商还是零售商提供以旧换新服务,制造商通过设计相应的契约都可以实现供应链协调,使闭环供应链系统利润达到最优,且制造商和零售商都能获得比分散决策下更高的利润。由表1可知,这说明,模型M 和R 下的补偿额的选择区间相同。采用与图3相同的参数,图5则直观地反映了两种模型下可以实现闭环供应链有效协调的区间范围。

图5 模型M 和R 下的有效协调区域Fig.5 The effective coordination regions under models M and R

命题2和3的结论为供应链成员因为提供以旧换新服务而产生冲突或“搭便车”现象给出了两种不同的解决方案,这可以为企业管理者提供决策参考。具体地,如果双方仅仅是希望通过提供以旧换新服务获得比无以旧换新时更高的收益,则简单的以旧换新补偿机制便可实现;如果在供应链以旧换新情形下双方还希望克服双重边际化问题,则建议制造商以集中决策的最优结果为基准,利用本文所设计的供应链协调契约进一步提升双方的收益。

5 结论

以旧换新促销不仅可以促进新产品销售,而且可以回收废旧产品,但企业提供以旧换新服务将产生一定的固定成本。为此,本文考虑闭环供应链中制造商可以自主提供以旧换新服务或让零售商提供以旧换新服务,提供者需承担相应的固定成本,由此探讨固定成本对以旧换新定价及渠道决策的影响。研究发现:

(1) 闭环供应链中不论是制造商还是零售商提供以旧换新服务,新产品零售价不变,且比无以旧换新服务时的零售价更高。这说明,提供以旧换新服务对初始消费者不利。两种以旧换新模型下的以旧换新折扣相等,故再次消费者购买新产品支付的实际价格比无以旧换新时的价格低,因此,再次消费者希望有以旧换新服务存在,但并不关心由谁提供以旧换新服务。

(2) 固定成本是影响制造商和零售商是否提供以旧换新服务的关键。较低的固定成本将使得制造商和零售商都愿意提供以旧换新服务,由此导致双方陷入冲突;而当双方的固定成本都处于中等水平时,双方又都希望由对方提供以旧换新服务,此时双方会产生“搭便车”现象。当制造商提供以旧换新的固定成本较低而零售商提供以旧换新的固定成本较高时,制造商提供以旧换新对双方都有利,反之亦然;当双方提供以旧换新的固定成本都较高时,双方都不愿提供以旧换新服务。

(3) 当固定成本较低时,提供以旧换新服务时的闭环供应链系统利润都高于不提供以旧换新服务时的系统利润。针对制造商和零售商在提供以旧换新方面可能存在冲突或“搭便车”现象,双方都可以通过补偿对方让其放弃提供以旧换新来消除冲突,或通过补偿对方让其提供以旧换新来消除“搭便车”现象。这种补偿机制可以使得闭环供应链系统利润在成员间再次分配,但闭环供应链系统总利润并未得到改善,仅比无以旧换新服务时更优。为此,针对两种以旧换新模型,通过设计相应的供应链契约,可以使得闭环供应链系统利润达到集中决策时的水平,各成员的利润也比分散决策时更高,从而实现闭环供应链协调。

本文所得结论的管理启示:

(1) 对于闭环供应链中的制造商和零售商而言,双方都应该对提供以旧换新服务产生的固定成本以及由此带来的额外收益进行权衡,以确定是否提供以旧换新服务。

(2) 当固定成本在可接受范围内时,不论是制造商还是零售商提供以旧换新服务,当出现以旧换新冲突或“搭便车”情形时,建议以旧换新受益方给予另一方适当补偿或双方通过供应链协调契约来消除冲突或“搭便车”问题,从而确保不仅双方都能从以旧换新活动中受益,而且供应链效率也能得到提升。

(3) 以旧换新服务提供者可以采取多种方式(如拆解再利用、再制造或翻新后再售)对旧产品进行处理,以最大程度地获取旧产品的剩余价值,从而扩大提供以旧换新服务的优势。

进一步的研究可以考虑将该问题扩展到存在制造商竞争或零售商竞争的情形。此外,现实中有不少第三方企业也会提供以旧换新服务,如爱回收、Gazelle、Nextworth等,下一步可研究存在第三方以旧换新服务提供商时对制造商或零售商提供以旧换新与否的影响。最后,本文假设对参与以旧换新的消费者给予相同的以旧换新折扣,未考虑消费者手中的旧产品可能存在质量差异问题,未来可进一步探讨如何根据旧产品质量不同实施差异化的以旧换新折扣,以更贴合实际。

附录

模型M 和模型R 的求解思路与模型N 类似,不再赘述。

推论1的证明

命题1的证明由T1、T2和T3的关系,易得命题1。

推论3的证明由命题1易得推论3。

推论4的证明当固定成本FM=FR=0时,通过比较3种模型下的最优利润可得推论4。

推论5的证明通过比较集中决策和分散决策下的闭环供应链系统利润,易得推论5。

命题3的证明在模型M 下,制造商可以通过设计契约给予零售商相对较低的批发价wC,同时让零售商给予制造商额度为的补偿。基于此,两企业的利润函数分别为: