仿枪虾虾螯纵向混合负泊松比结构设计与耐撞性研究

杨 欣,王瑞祥,2,许述财,秦豪毅,2,宋家锋,4,5

(1.河北农业大学 机电工程学院和长城汽车学院, 河北 保定 071001;2.清华大学苏州汽车研究院(相城), 江苏 苏州 215134;3.清华大学 汽车安全与节能国家重点实验室, 北京 100084;4.吉林大学 工程仿生教育部重点实验室, 长春 130022;5.运输车辆检测、诊断与维修技术交通行业重点实验室, 济南 250357)

0 引言

随着汽车数量的增多,人们对汽车安全的要求越来越严格。在被动安全领域中,研究者不断探究新型吸能结构如薄壁管、夹层板、负泊松比蜂窝结构等来吸收碰撞冲击能量,保护人员安全[1]。负泊松比结构具有高比刚度/强度和优良的抗冲击性能,在航空航天、机械工程、军工等领域应用较广[2]。至今为止,国内外学者已对负泊松比结构做了大量的研究。

国外研究负泊松比结构较早,在1987年,科学家Lakes等[3]在实验室中人工合成了第一个负泊松比材料。自此,负泊松比结构和材料被广泛熟知与研究。Gibson等[4]最早设计出内凹六边形的负泊松比结构,确定了负泊松比结构最低的内凹角度。后续的研究中相继提出了星形胞元结构、双箭头胞元结构和正弦曲边胞元结构等。例如Grima等[5]在2005年评估了一种由不同旋转对称的星形单元组成的二维周期结构的拉胀行为,最终认定此结构具有负泊松比效应。Larsen等[6]设计出双箭头结构,实现了材料结构和柔性机制的自动设计。Dolla等[7]在研究心血管支架球囊血管成形术时,设计了一种独特的外延负泊松比支架结构,是首例正弦曲线负泊松比结构。国内对负泊松比结构的研究晚于国外,沈建邦等[8]设计了一种具有负泊松比效应的可变弧角曲边内凹蜂窝。虞科炯等[9]设计了一种具有正弦函数曲线构型的负泊松比蜂窝结构,并研究了冲击速度和微结构几何参数对结构变形和吸能的影响。尤泽华等[10]设计了变弧边内凹多胞蜂窝负泊松比结构,并对其面内动力学性能、能量吸收特性和平台力进行讨论,结果显示,结构的能量吸收与平台应力受单胞角度与冲击速度的影响。王振等[11]基于旋转刚体结构与内凹多边形结构的变形原理,通过旋转常规的内凹多边形,得到了一种旋转内凹六边形的负泊松比结构,提升了负泊松比结构的力学性能。此外,还有圆弧曲边六边形结构[12]、新十字负泊松比结构[13]、厚度梯度[14]等新型负泊松比结构。

近年来,工程仿生学成为研究热点,在汽车被动安全领域中,仿生结构较传统结构提升了吸能效果。受空竹启发,刘海涛等[15]提出一种空竹型负泊松比蜂窝结构,与传统的内凹六边形相比,空竹型蜂窝结构具有更高的平台应力和比吸能。任毅如等[16]仿照椰子树同心结构,设计了负泊松比梯度同心拉胀内凹蜂窝结构,梯度同心结构同样拥有更高的比吸能和平台应力。还有仿蝴蝶翅膀[17]、仿蛛网同心[18]等仿生负泊松比结构。

综上所述,仿生负泊松比结构拥有优良的耐撞性能,但现有负泊松比结构胞元单一,混合胞元负泊松比结构研究较少。受枪虾捕食特点及虾螯微观结构启发设计混合胞元仿生负泊松比结构[19],分析其耐撞性吸能指标,并选取最优混合结构。

1 仿生原型分析与结构设计

1.1 仿生原型分析

枪虾学名Alpheus heterochaelis,因其虾螯可发出冲击波击晕猎物而得名,成年枪虾最大体长可至8～10 cm,生活在热带海洋中。虾螯一大一小,大的用以捕食,小的用来进食[20]。枪虾在捕猎时,大螯外侧螯爪迅速闭合,圆柱形凸起迅速插入定螯空穴之中,挤出的水柱以大约30 m/s的速度冲击周围海水及螯壁形成气泡,在极短的时间内(600 μs)破裂,发出巨大的爆炸声和冲击波[21-22],枪虾以此方式击晕猎物获取食物,但自身并不会受到伤害。用扫描式电子显微镜观察虾螯内部结构如图1。观察其动螯断面结构发现,从内到外分3层结构,分别为密实化结构、大孔隙率结构和纵向小孔隙率结构。而且各层微观结构与数学几何中的圆弧曲线、正弦曲线极为相似。受此启发,在负泊松比吸能结构的研究中设计相应仿生结构,并进行混合,研究其吸能性和平台应力。工程仿生设计中,常常以结构、载荷和功能这3个方面来评价生物原型与所设计工程结构的相似程度,相似程度越高表明仿生设计越有效。

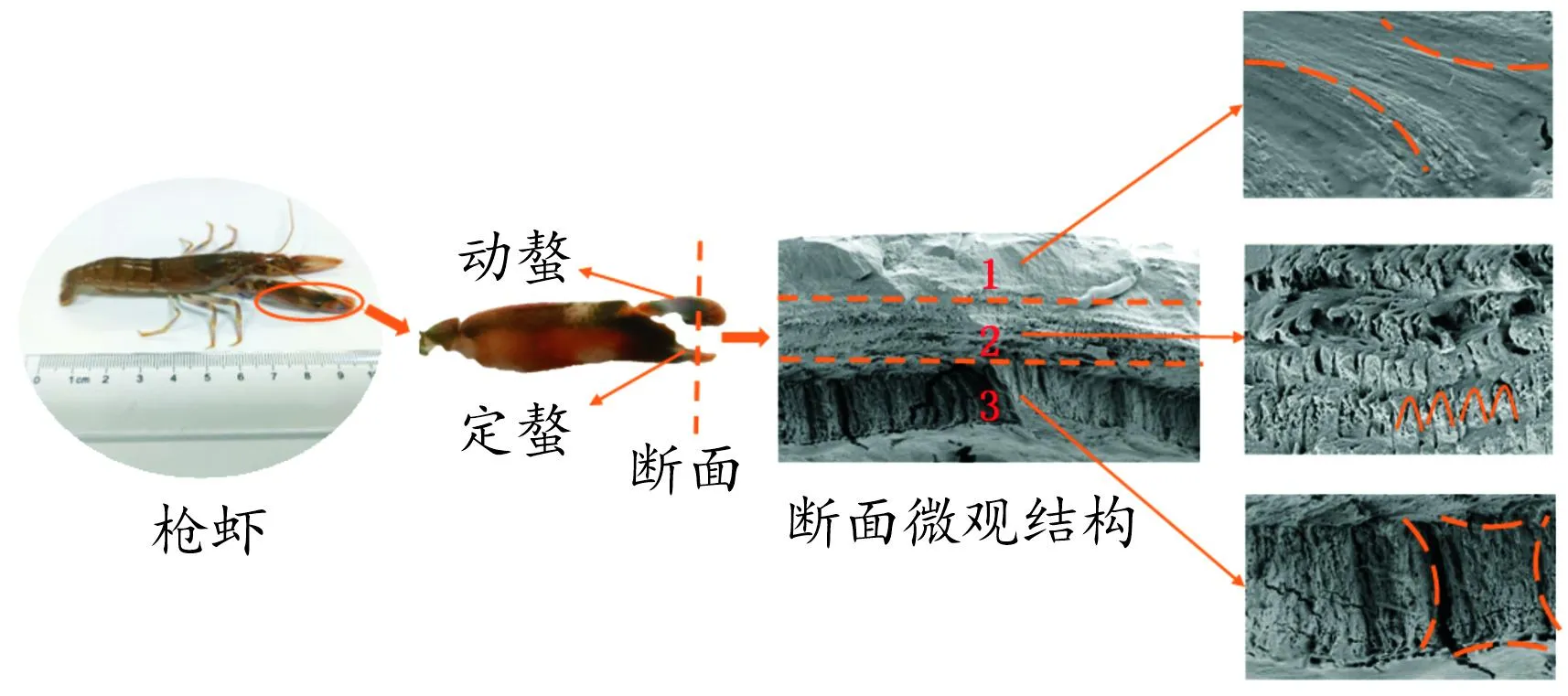
图1 枪虾生物微观结构示意图

1) 结构相似性:负泊松比结构可看成单胞阵列,整个芯体作为主要缓冲吸能结构,吸收冲击能量。枪虾大螯同样是内部生物组织作为缓冲结构,吸收能量。虾螯的结构与负泊松比结构在设计的思路上颇为相似。

2) 载荷相似性:负泊松比结构在应用的过程中,实际上会受到来自不同方向的力,最理想的状态是受到垂直于顶端的力,通过最上层的胞元结构层层传递至下层。枪虾大螯受到冲击时,各个方向的力作用在最内层曲面上,可将其简化为极小平面受力,垂直或者成一定的角度,一层受力后向下一层传递。

3) 功能相似性:枪虾的大螯和负泊松比结构受到冲击力的作用时,枪虾的大螯通过接触层向内部传递,通过每层不同结构生物组织规则或者不规则的变形吸收能量,从而保护自身不受伤害。负泊松比结构通过自身的弹塑性变形吸收能量,从而起到吸能防护的作用。

1.2 仿生结构设计

对枪虾动螯与定螯进行生物研究,虾螯用液态氮迅速冷冻后,在断面处,利用扫描式电子显微镜观察断面内部结构。继续放大发现各层结构均有相似的几何形状,最外层轮廓呈现类似对称圆弧,中间一层可见明显的层级结构且中部弯曲与正弦曲线相似,最内层横向排列,观察发现可视为若干个4边圆弧组成的单元,且相邻圆弧尺寸不同,相对圆弧尺寸基本一致。由此设计以具有的相同尺寸与角度的内凹六边形负泊松比蜂窝A、正弦曲边负泊松比蜂窝B、圆弧曲边负泊松比蜂窝C、四弧边曲边负泊松比蜂窝D作为基础胞元,为方便后续研究,以大写字母代替命名,如图2所示。图2中各胞元上边长L1=L2=L3=L4=L=20 mm,侧边l1=l2=l3=l4=l=20 mm,厚度t1=t2=t3=t4=t=1 mm,为保证所设计的模型为负泊松比结构,以图中a值(侧边内凹深度)保证内凹蜂窝胞元角度不得低于120°。经过计算,其最小值为,a1=a2=a3=a4=a=5.8 mm。因各结构尺寸相同,以下用a、l、L、t分别代表内凹深度、侧边长、上边长和厚度。

图2 4种负泊松比单胞结构

结合枪虾虾螯微观结构与层级混合思想,将4种胞元结构纵向混合成为整体结构,胞元设计为双层形式,横向11个胞元,纵向8个胞元,分4组,每组胞元结构各不相同。与基础胞元结构相同的层用相同字母表示,如图3所示,混合结构命名为ABCD。原结构为AAAA改变图中结构顺序,在横向上加筋板,板长L/2。根据排列组合原理设计出ABDC、ACBD、…、DCBA等24种不同顺序的负泊松比结构。

图3 混合结构ABCD与原结构AAAA

2 有限元模型的建立与验证

2.1 有限元模型建立

根据美国保险公司的数据,低速碰撞(速度在16 km/h以下)是发生最多的事故[23]。在中国城市交通中,由于车流量大,车道较窄,发生碰撞事故时速度更低[24](文中选取v=2 m/s)。应用有限元建模与求解软件进行仿真分析,根据低速冲击工况与前人研究成果设置有限元模型,如图4所示。模型主要由冲击端、约束端、中间芯体结构组成,冲击端赋予向下的恒定速度v=2 mm/ms,并约束除Y方向以外的速度方向,下面板全约束处理。在冲击端、约束端与芯体接触处设置SURFACE TO SURFACE自动接触,设置芯体SINGLE SURFACE自动接触,动摩擦为0.2,静摩擦为0.3,真实的工况中冲击端与约束端板面变形较小可忽略不计,两端设置为刚体,材料设置为MAT20。芯体结构使用Belytschko-Tsay壳单元,节点数目为4,积分点数目为5,材料设置为MAT24。本研究中负泊松比结构的材料为AA6061-T6铝合金,密度2.73×103kg/m3,泊松比为0.33,弹性模量为68.2 GPa,屈服强度取252 MPa;上下面板密度2.78×103kg/m3,泊松比为0.3,弹性模量为210 GPa[25]。

图4 有限模型示意图

2.2 耐撞性评价指标

碰撞防护中,常用比吸能SEA(specific energy absorption)、初始峰值载荷IPF(initial peak force)、平均压溃效率CFE(crushing force efficiency)作为主要的吸能防护指标[26-27]。负泊松比结构属于多孔蜂窝结构,相对密度与平台平均应力[28](mean stress of platform)也会被众多研究者选择评价。SEA不受结构尺寸的限制,仅与结构质量和吸能有关,表示单位质量条件下能量吸收的能力,单位 kJ/kg,公式如下:

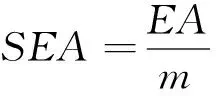
(1)

式中:EA表示结构变形过程中吸收的全部能量,kJ;m表示结构的质量,kg;EA计算方法如下:

(2)

式中:f(x)是结构变形过程中所受载荷随着位移变化的函数;a和b分别为积分计算的初始位置与结束位置。

平均压溃率效率是衡量防护结构吸能稳定性的指标,如下:

(4)

式中,Fp是所选区域内的平均载荷,kN。

初始峰值载荷IPF(initial peak force)是在选定的计算区域内第一个载荷峰值点,通常情况下要求吸能结构拥有较小的IPF、较大的SEA与CFE。

多孔材料的相对密度公式:

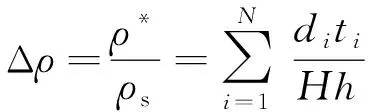
(5)

式中:ρ*为负泊松比蜂窝结构的表观密度;ρs为负泊松比蜂窝结构基体材料的密度;N为结构曲线的数量;di、ti分别为第i根曲线的长度和厚度;H、h分别为整体蜂窝的长度和宽度。

平台应力作为负泊松比结构的另一个评价指标。

名义应力计算公式:

σ=F/S

(6)

式中:S表示结构与刚体之间的接触面积,即面外厚度与水平长度的乘积;F表示刚体与蜂窝结构之间的接触力。

蜂窝结构的平台应力表示为:

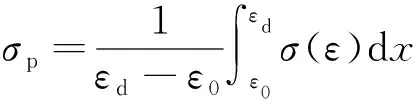
(7)

式中:ε0为初始峰值载荷时的名义应变;εd表示锁定应变,为再次达到与峰值载荷相同应力的应变。

2.3 有限元模型的验证

在可以保证实验精度和准确性的前提下,缩小样件的尺寸进行验证[29-30]。采用5层结构,Inventor软件建立模型,通过线切割方式制作,又因为所选材料应变效应不明显,实验时用恒定速度10 mm/min进行准静态压缩仿真试验,使用电子万能试验设备,现场试验与仿真结果如图5所示。

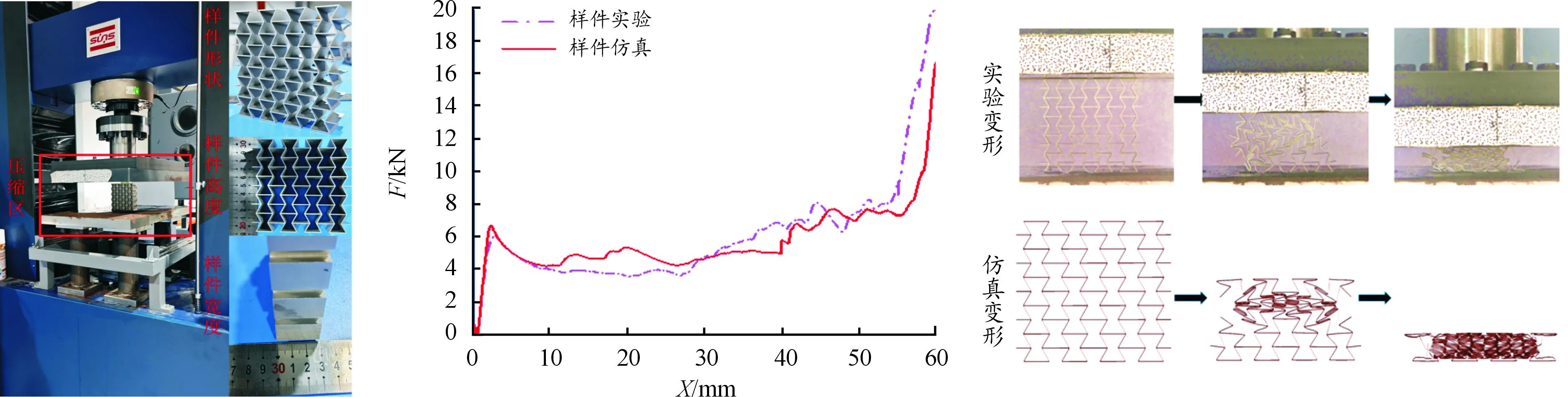
图5 样件验证试验及载荷变化曲线

由图5可知,试验和仿真的曲线趋势极为相似,并且仿真的峰值点和实验的峰值点能够清晰地捕捉对应,上述评价指标的误差如表1所示。其中最大的误差项是质量m,为6.67%,小于10%,这是工程试验所能接受的,由此说明建立的有限元模型是可信的。

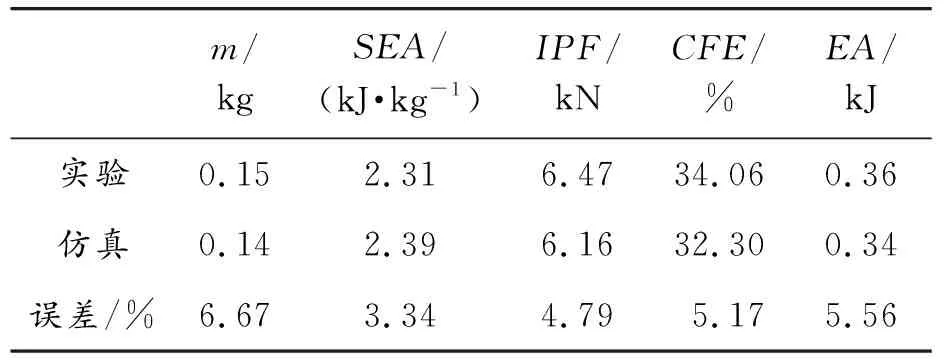
表1 实验误差分析

3 仿真分析

3.1 数据指标分析

4种各组拥有相同胞元的负泊松比结构耐撞性评价指标计算如表2所示(压缩率65%),平台应力计算如表3所示。

表2 4种相同胞元结构耐撞性指标

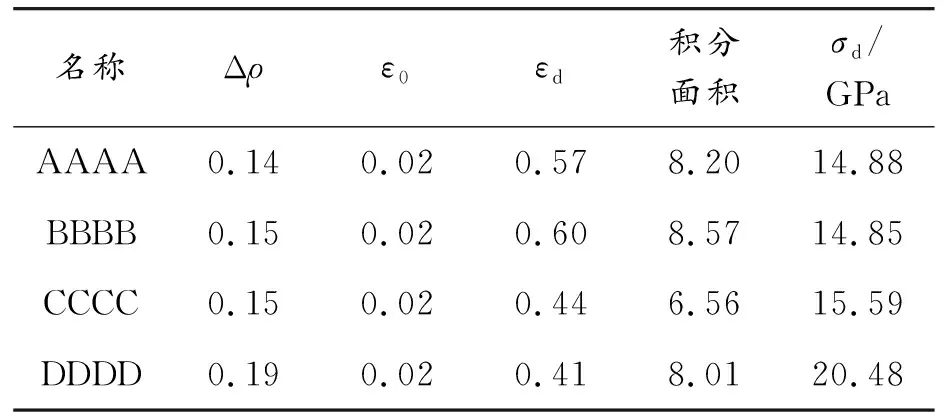
表3 4种相同胞元结构平台应力

从表2可以看出:AAAA蜂窝结构拥有较低的SEA和IPF,但是具有最大的CFE,为59.26%;DDDD蜂窝结构拥有最高的SEA和IPF;CCCC蜂窝结构IPF与CFE最小;DDDD蜂窝结构指标均在其他3种之间。在平台应力相关指标中,结构相对密度按照表3从上到下顺序呈现上升趋势,名义应变均在0.2～0.3之间,锁定应变基本在0.6以下,这说明设计的蜂窝结构由于自身的结构特点吸能阶段较短,进入密实化阶段较快。平台应力与相对密度具有相同的趋势,均随着结构的改变有所提高。在实际的吸能防护结构中,按照耐撞性的要求,最为理想的结构需具有较大的SEA和CFE,较小的IPF。

本研究融合仿生思想将4种结构进行混合搭配。设计了24种混合结构进行仿真分析(结构设计在1.2节)其结果如表4所示。由表可知,与上述4种相同胞元蜂窝结构相比,混合结构各数据指标均有所变化,首先,混合结构的质量分为0.37 kg与0.38 kg两种,出现2种质量是因为胞元D在混合结构的位置不同引起的,当胞元D在结构纵向内侧时,纵向相邻圆弧边与直线边都会被保留,此时质量增加。耐撞性指标中IPF最小值为9.66 kN,相比最低值降低了3.71%,比最高值降低了27.13%;SEA最高值为3.00 kJ/kg,与上述最低值相比升高了19.85%,与最高值相比降低了5.66%,平台应力虽然也有变化,但从表格可以看出,各结构的平台应力相差较小,除去误差与精度的影响,混合结构对平台应力的影响不大。其他数据指标均有范围变化,这就说明结构的混合设计确能影响结构吸能性能。

表4 混合结构耐撞性指标

3.2 变形分析

结构整体的变形模式与文献中相似,重点在于混合结构的变形吸能。混合结构共有24种,选取胞元模型AAAA和DDDD以及拥有SEA值最大的BCDA、CFE值最大的BDAC、IPF值最小的ADCB 3种混合蜂窝结构模型分析其变形过程。图6为各结构冲击位移在0、20、40、80、104 mm处的变形。

图6 AAAA、DDDD、BCDA、BDAC、ADCB(上至下顺序)仿真变形图

从图6可以看出,AAAA型结构在压缩20 mm处出现“X”形变形,随着冲击板继续下压,结构变为波浪状,大变形区域集中在一侧,DDDD型结构变形不明显,在冲击端压溃后整体向左侧偏移,随着压缩继续进行,在压缩量80 mm处出现3条“>”状压实区域,逐渐密实化。3种混合模型的变形过程均经历“V”型与“X”型,只有BCDA结构出现波浪状,并且3种结构都是从BBBB结构与CCCC结构的交界处开始变形,后转入AAAA结构处,最后是DDDD结构。BCDA型结构变形整体与DDDD结构相似,出现3条“>”最终压实。BDAC与ADCB结构变形与上述其他结构不同,这2种结构没有出现结构向一侧偏移的情况,在x=80 mm处出现上下2个变形密集区,中间胞元D层隔开。综上,胞元B与胞元C受到冲击时峰值载荷较低,承受压溃能力较弱,而胞元D拥有较大的抗冲击能力而不易变形;在受到冲击力作用时混合结构相对于单一胞元结构更加稳定,对结构的稳定性有积极的作用。混合结构的平台应力均在15 GPa左右,并没有较大的范围变化。经过仿真分析,改变结构顺序并不会对平台应力有较大影响。

4 最优结构选择

考虑到耐撞性指标的不唯一,并且各个指标均有劣势区和优势区,SEA、IPF、CFE的最优指标并不会集中在一个结构上;又因为4种结构中正弦结构没有内凹角度,选取内凹深度a(1.2节a1、a2、a3、a4)作为优化的参数,用3个指标的加权组合来综合评价结构耐撞性,选取最优结构[31]。

在24种混合结构中,为保障优化的精度,选取每个耐撞性指标的3个最高值模型作为优化模型,共9种。本研究中负泊松比结构最低值为a=5.8 mm,以0.5 mm为步长设置6.3、6.8、7.3 mm 4个参数,继续取值会影响实物制作。对所增加的27种模型进行仿真分析,如图7所示。

图7 9种结构仿真图

从图7可以看出,在所选区间内a值越大,所设计的混合结构的IPF越低,且各结构数值均下降,整体呈单调趋势;SEA值在各结构中表现复杂,部分结构随着a值增加,SEA值也随之增加,但是也有部分结构SEA值会降低;CFE值在a值增加后,少部分结构会随之增加,而绝大部分均呈现下降趋势。采用加权组合综合选取最优结构,公式如下:

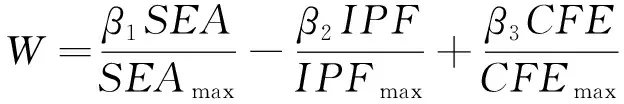
(8)

式中:β1+β2+β3=1。在实际防护作用中,结构的SEA是主要指标,IPF和CFE是重要指标。因此,设置β1=0.4,β2=0.3,β3=0.3作为3个评价指标的权重因子[32]。SEA、IPF、CFE三个指标的单位不同,进行归一化处理,图8为各结构在不同a值下的权重值。

图8 不同a值各结构的权重值

由图8可知,BCDA权重值只在a=6.3 mm处低于ACDB和ADBC结构,并且在a=6.8 mm时权重值最大,为0.41。综上所述,选择a=6.8 mm时的BCDA结构作为最优结构,优化后SEA=3.21 kJ/kg,IPF=8.58 kN,CFE=31.29%。建立以0.2 mm步长,壁厚为0.6～1.8 mm的BCDA模型,仿真结果显示壁厚t与耐撞性指标正相关,因此,尺寸不进行优化。

5 结论

1) 通过研究枪虾生活习性与枪虾捕食特点,选取虾螯作为仿生原型,以扫描式电子显微镜提取内部微观结构,设计了24种仿生纵向混合负泊松比结构,研究其耐撞性能。

2) 以SEA、IPF、CFE作为评价指标,使用经过验证的有限元模型对结构进行低速冲击仿真模拟,基础胞元结构中,3个指标最优结果各自分散,没有集中在同一结构。混合结构中,耐撞性能优劣也各不相同,变形稳定性强于基础结构。

3) 选取9种高指标结构,以内凹深度a作为参数进行优化,选择内凹深度a=5.8、6.3、6.8、7.3 mm作为设计变量进行仿真分析,采用加权组合综合评价各结构耐撞性,结果显示混合结构BCDA在a=6.8 mm时为最优结构,此时SEA=3.21 kJ/kg,IPF=8.58 kN,CFE=31.29%。