改进的Mertens第一定理估计及应用

苑金臣, 王军霞, 郭艳凤

(中国地质大学 数学与物理学院, 湖北 武汉 430074)

0 引言

众所周知,Mertens公式是数论中研究素数分布理论的基本公式, 1874年由德国数学家Mertens首先用初等方法得到。Mertens公式具体表示为

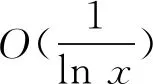
定理1(Mertens第一定理[2-3]) 对x>2,p为素数,有

式中:O(1)项取值在开区间(-1-ln 4,ln 4)中,(ln 4≈1.386 29)。

文献[3]只讨论了得到的上界:

文献[4]研究了定理1的估计区间。 关于Mertens第一定理的研究还有很多,然而所得的结果还可以更进一步优化相应的估计。

Mertens第一定理中的估计区间还没有达到更好的临界点。为了更进一步提高Mertens第一定理中估计区间的精度,对定理的应用有更好的结果,还需要不断地对估计区间进行精细化。 本文在Mertens第一定理的基础上,利用经典定积分估计的主要思想及Stirling’s公式的应用[5-9],对Mertens第一定理中的估计不等式中的区间进行了改进。此改进的结果把文献[3-4]中的估计区间进行了缩小,得到了更精细的Mertens第一定理中上界的估计。 这是对Mertens第一定理本质的改进,在应用方面利用该细致的估计会得到更加好的结果。

1 预备知识

本文的主要结果证明是从简单的定积分思想和一些重要的不等式出发,经过精确地估计,得到更加精细的结果。众所周知,定积分的思想可以应用在求解无穷级数的和。为了证明本文中的主要结果,就需要对所研究的计算进行估计,并应用定积分来估计。另外证明过程中还需要用到文献[2]的主要关系式。 这些关系式为

(1)

(2)

2 主要结果

定理2(改进的Mertens第一定理) 设p为素数,则有改进的Mertens估计不等式:

(3)

(4)

证明分别从左右两侧进行估计的证明。

1) 证明不等式(3)。

因为函数f(x)=lnx的图形是上凸的,由其几何意义可知,梯形面积小于曲边梯形面积,于是可得

lnn!=ln 2+ln 3+ln 4+…+

ln (n-2)+ln (n-1)+lnn=

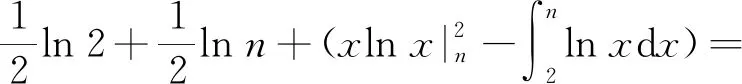
从而有

(5)

利用文献[2]中的方法,可得

(6)

结合式(1)、式(5)和式(6),可得下面不等式:

(7)

又因为

所以

化简式(7),可得

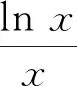
又由于

则有

这就证明了式(3)。

2) 证明不等式(4)。 根据已知Stirling’s公式,通过优化的放缩估计得到。 由Stirling’s公式

两边取对数,可得

从而有下面不等式

(8)

关于不等式(8)右端最后一项,有估计式[4]:

又因为

于是从式(8)可得

(9)

当n≤3时, lnn≤1。由式(9)可得

(10)

这就证明了不等式(4)。 证毕。

3 改进定理的应用

引理1令

于是,对x≥2,有

(11)

式中:θ=θ(x)∈(0,1)。

定理3存在常数c1,使得对x≥2有

(12)

证明由改进的Mertens第一定理(定理2),对t≥2有

此外,

这里对含有R(t)的积分是采用Abel求和法。

令

由改进的Mertens第一定理的上界估计,可得

于是可取常数

从而定理3得证。 证毕。

注1 在证明过程中可选Landau记号中的常数M为不大于1.285 6的数。

4 结束语

利用定积分的性质和一些重要的不等式,对Mertens第一定理的估计进行了细致的推导和估计,得到了更加精确的估计区间,给出了改进的Mertens第一定理。相比定理1中的估计区间有所缩小,对定理1进行了比较大的优化估计,提高了估计精确度。根据改进的Mertens第一定理的结果,应用到一个渐近公式中,提高了证明过程中Landau记号M的精确范围。然而,通过定理的证明过程可以看到,改进的Mertens第一定理得到的估计还没有达到Mertens第一定理的临界点,还可以进一步进行优化。这就需要通过其他的方法来寻找其估计的临界点状态,未来将进一步改善该估计区间,从而得到更好的应用。这是一个具有挑战性的工作。