基于自适应滑模的欠驱动无人艇轨迹跟踪控制算法

姜 涛，陈 宇，周兴阁

(同济大学 机械与能源工程学院，上海 201804)

0 引言

水面无人艇是一种能够自主航行并完成一系列任务的智能化水面平台，因其具有安全性高、可靠性强、工作效率高、体积小且造价低廉等优点，被广泛运用于科学研究、海水检测和海上侦察搜索等领域，具有广阔的应用前景[1-3]。

近年来，随着计算机及控制技术的进一步发展，水面无人艇的工程应用及理论研究取得了突破性进展。然而，随着海洋工程的不断进步，在水面无人艇的运动控制领域内仍然面临着巨大挑战。首先，复杂的海况使无人艇在建模时不仅需要考虑海水的推力，还要考虑涌流对系统的影响，同时海面上巨大的风浪对水面无人艇的运动控制也会产生不利影响；其次，无人艇的动力输出结构决定了水面无人艇的控制输入维度小于无人艇运动自由度数，是一种典型的欠驱动系统，目前常见的一些控制方法无法直接运用于水面无人艇；此外，无人艇是一个高度耦合的水文系统，受船体参数摄动、质量变化、动力学模型中存在动态不确定项等因素的影响，精确的无人艇模型难以建立，加之执行器饱和、故障等情况，对无人艇系统进行稳定、快速、准确的控制具有高度的挑战性[4-6]。

无人艇的轨迹跟踪问题，即为无人艇设计一个合适的控制器，使无人艇对于任意给定的初始状态，其可以在执行器输入的作用下沿着所给出的期望轨迹进行跟踪运动。无人艇的轨迹跟踪是无人艇控制领域的热点问题。与路径跟踪问题不同，无人艇的轨迹跟踪控制受到时间的约束，即要求被控对象在指定的时间到达期望轨迹上相应的位置。由于无人艇本身是一个非线性的欠驱动系统，且需要考虑诸多干扰因素和其对于无人艇轨迹跟踪效果的影响，因而目前的欠驱动无人艇运动控制算法主要采用自适应控制、反演控制、滑模控制、预测模型控制和神经网络控制等智能控制算法[7-13]。

陈霄等[14]针对三自由度欠驱动无人艇的路径跟踪问题，设计了一种基于视线制导律(LOS)的跟踪控制算法；张昕[15]将滑模控制与反步法结合提出了一种欠驱动无人艇轨迹跟踪控制算法，并通过MATLAB仿真验证了算法的有效性。Wanga等[16]针对无人艇的模型不确定性问题，采用了RBF神经网络对不确定动力参数项进行了逼近，实现了模型参数摄动条件下无人艇的航向控制问题。Li等[17]提出了一种基于LOS的可在有限时间内收敛的路径跟踪策略，并设计了有限状态观测器和辅助系统实现了欠驱动无人艇在速度未知和执行器饱和等条件下的路径跟踪控制。Huang等[18]在LOS路径跟踪制导律的基础上设计了一种新的欠驱动无人艇轨迹跟踪制导律，并考虑了外界风浪流干扰对系统产生的影响，有效提高了欠驱动无人艇的跟踪性能。

基于上述文献的分析，目前对于外界干扰未知、模型存在不确定性和执行器故障等条件下的欠驱动无人艇轨迹跟踪控制问题的研究相对较少。本文提出了一种基于扰动观测器与神经网络技术的轨迹跟踪控制策略，并采用自适应滑模控制律应对可能出现的执行器衰减故障问题，实现了较为复杂环境条件下欠驱动无人艇的轨迹跟踪控制问题，具有一定的参考意义和应用价值。

1 问题描述

1.1 欠驱动无人艇的三自由度数学模型

为了完整准确地建立无人艇的运动学和动力学模型，通常需要建立两个不同的坐标系。如图1所示，O0-X0Y0Z0为惯性坐标系，O0为坐标原点，O0X0轴指向正北方向，O0Y0轴指向正东方向，O0Z0竖直向上，惯性坐标系主要用于描述无人艇的位姿信息；O-XYZ为船体坐标系，O为坐标原点且通常为无人艇的重心，OX轴指向艇首方向，OY轴指向艇的右舷方向，OZ轴指向艇的顶部方向，船体坐标系适合描述艇的速度和受力信息，因而无人艇的动力学模型方程一般建立在船体坐标系上。

水面无人艇在实际的航行过程中共包含6个自由度，分别为纵荡、横荡、垂荡、横摇、纵摇和艏摇。但由于六自由度的无人艇模型较为复杂，不利于轨迹跟踪控制器的设计和研究，因而在实际的应用中，通常会忽略无人艇的垂荡、纵摇和横摇这3个在无人艇轨迹跟踪控制问题中影响较小的自由度，从而将问题简化为三自由度的平面运动控制问题。如图2所示，欠驱动无人艇在前进推力和转向力矩的作用下航行。我们假设无人艇的质量分布均匀且结构左右对称，同时忽略地球自转对无人艇产生的加速度影响，则欠驱动无人艇的三自由度数学模型可以表示为[19]

图2 无人艇的三自由度模型

图3 视线制导律的基本原理

(1)

其中：(x，y，r)为惯性坐标系下无人艇的横坐标、纵坐标和航向角，(u，v，r)为船体坐标系下无人艇的横向速度、纵向速度和航向角速度，(m11，m22，m33)为无人艇的惯性质量系数，(d11，d22，d33)为无人艇的阻尼系数，(τu，τr)为执行器实际作用在无人艇上的推力和转向力矩，(wu，wv，wr)为外界风浪作用在无人艇上的横向干扰力、纵向干扰力和干扰力矩。

无人艇在实际的航行过程中，执行器可能发生故障从而导致控制系统的稳定性和动态性能受到影响。由于执行器卡死情况的发生会使系统不可控，在此不予分析。本文仅讨论执行器衰减故障产生的影响，并假设有

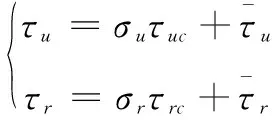
(2)

1.2 控制目标

假设给定的期望轨迹变化光滑的前提下，考虑外界风浪流干扰、执行器衰减故障和模型参数不确定性等因素对无人艇产生的影响，设计一个合适的欠驱动无人艇控制器，使其在惯性坐标下的位姿满足

(3)

2 欠驱动无人艇轨迹跟踪控制器设计

如图4所示，本文设计的轨迹跟踪控制系统主要由视线制导律，自适应滑模控制器，非线性扰动观测器和RBF神经网络四部分组成。控制系统首先根据制导律得到无人艇期望的航向角和前进速度，确保无人艇的位置可以收敛到期望轨迹。再通过自适应滑模控制器跟踪期望的航向角和前进速度，并抑制执行器衰减故障产生的影响。同时，通过非线性扰动观测器对未知外部海洋环境干扰进行在线估计，以此提高无人艇轨迹跟踪控制系统的鲁棒性。最后，利用RBF 神经网络的逼近特性，对模型中的不确定动态项进行在线估计，降低因模型中存在的不确定动态项对控制系统性能的影响，从而实现对无人艇的精准控制。

图4 无人艇轨迹跟踪控制器系统框图

本文的控制器设计方法将神经网络技术与扰动观测器技术相结合，使设计的无人艇轨迹跟踪控制器同时继承了以上两种技术的优良特性。通过引入神经网络技术解决了欠驱动无人艇动力学模型中存在不确定动态项的问题，同时结合扰动观测器技术，使得未知外部扰动能够被观测器估计出来进而补偿到前馈控制网络中，从而提高控制系统抵抗外部环境扰动的能力。

2.1 欠驱动无人艇制导律设计

传统的欠驱动无人艇轨迹跟踪策略大多基于反步法或 PID控制法进行设计。但由于无人艇模型是一个复杂的非线性欠驱动系统，直接对其控制律进行设计是一个难题，通常会出现较为复杂繁琐的虚拟控制量，这使得控制器在实际的应用中受到了限制。为了降低控制系统设计的复杂度，确保无人艇可以准确跟踪期望轨迹，本文在视线制导律的基础上设计了一种适用于轨迹跟踪的新的制导策略，使无人艇可以在时间参数的约束下到达相应的位置。

视线制导律的基本思想在于减小无人艇与期望路径之间的横向误差ye，根据横向误差的大小计算出相应的目标航向角，以减小无人艇与期望路径之间的距离，实现路径跟踪的目的。该方法因其结构简单易于理解和设计，且制导律仅与无人艇的实际位置和期望路径相关，不受限于系统的动力学模型，因而被广泛应用于欠驱动无人艇的路径跟踪控制系统中。

如图3所示，假设无人艇的期望轨迹曲线的表达式为Pd(xd(t)，yd(t))，则该路径上在t时刻的切向角ψd为：

(4)

定义无人艇相对于理想位置(xd，yd)的纵向跟踪误差xe和横向跟踪误差ye为：

(5)

对式(5)进行求导并将式(1)代入可得：

(6)

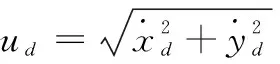
传统的视线制导律大多应用于欠驱动无人艇的路径跟踪控制系统，此时的期望路径表达式为Pd(xd(s)，yd(s))，其只与路径参数s相关，而与时间t无关。传统的视线制导律的表达式为

(7)

其中：ψp为期望航向角，Δ为前视距离。

式(7)中的制导律可以使欠驱动无人艇横向误差ye收敛，从而使无人艇跟踪期望路径，但由于该制导律的前向期望速度由人为设定，因而无法直接应用于轨迹跟踪控制问题，为了确保纵向误差xe收敛，设计如下的制导律

(8)

构造Lyapunov函数

(9)

对式(9)求导并将式(6)和式(8)代入可得

(10)

相较于传统的反步控制法、视线制导律和文献[18]中的轨迹跟踪制导律而言，本文提出的制导律有如下几点优势：

1)在传统视线制导律的基础上增加了期望速度的制导律，使其可以应用于欠驱动无人艇的轨迹跟踪问题，确保了无人艇与期望轨迹的横向误差和纵向误差均在有限时间内收敛至零。

2)设计的制导律中的期望速度up和期望航向角ψp可以直接通过前进推力和转向力矩的控制来完成，避免了反步法中将航向角和纵向速度耦合而产生的复杂虚拟控制量，降低了轨迹跟踪控制器的设计难度和复杂度。

3)增加了有限时间项sigρ(x)，该项可以使无人艇的实际的航向角与跟踪轨迹更为光滑，且可以有效降低无人艇制导系统的超调量，使无人艇的实际位置可以更快地收敛至期望轨迹。

4)对纵向跟踪误差xe进行了归一化处理，使制导律得到的期望速度更为合理，避免了文献[18]中纵向误差xe过大时，Up变为负数从而使制导律得到的期望速度超出无人艇所能达到的速度范围的问题，确保了无人艇制导系统在距离期望轨迹较远时的有效性。

2.2 非线性扰动观测器设计

无人艇在航行过中时会受到海风海浪等外界因素的干扰，这使得无人艇难以进行精确的控制。为了有效抑制外界的干扰，在无人艇的轨迹跟踪控制系统中通常会设计一个扰动观测器进行补偿。扰动观测器最基本的思想概念即设计一个能够估计不可测扰动的子系统，将其应用在前馈控制策略中，便可将外界未知的扰动量估计出来，并用估计量替代实际扰动量实现前馈控制策略，最终实现系统的精确控制。通过扰动观测器对未知外部海洋环境产生的时变干扰量进行在线估计，可以有效地提高无人艇轨迹跟踪控制系统抵抗外部环境干扰的能力，消除外界干扰对无人艇控制系统性能的影响。

对于水面无人艇在航向过程中受到的外界风浪流产生的未知时变干扰量wu和wr，可以设计如下形式的非线性扰动观测器：

(11)

(12)

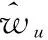
令观测误差为

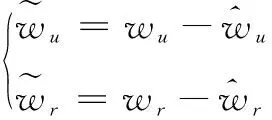
(13)

可以构造Lyapunov函数

(14)

对式(14)进行求导并将式(11)和式(12)代入，可以得到

(15)

由Young’s不等式，有

(16)

将式(16)代入式(15)中，可得

(17)

(18)

其中：

(19)

故所设计的非线性扰动观测器的误差是一致最终有界的，即扰动观测器是稳定收敛的。

2.3 RBF神经网络设计

无人艇是一个复杂的非线性系统，其在作业过程中，除去外界环境所产生的干扰外，其自身的动力学模型参数也具有高度的非线性和不确定性，这给无人艇的运动控制带来了很大的负面影响。为了抑制模型不确定性带来的扰动，本文采用了RBF神经网络对动力学模型中的不确定非线性项进行实时拟合，避免了水动力系数难以精确测定带来的困扰。

RBF 神经网络是一种具有单隐层的3层前馈神经网络，其能够以任意精度对任意未知非线性连续函数进行局部逼近，因而其可以对控制系统中的一些未知函数进行估计和补偿。该神经网络在学习过程上与BP神经网络相似，主要区别为两者使用的作用函数不同。由于BP神经网络在隐藏层中使用的是Sigmoid 函数，该函数在其输入空间无限大的范围内函数值非零，使得其具有全局逼近的特性；然而RBF神经网络则采用的是高斯基函数，在其输入空间有限范围内的函数值非零，使得该神经网络具有局部逼近特性。由于BP 网络是一种全局逼近神经网络，其在每次样本学习的过程中均需要对网络的所有权值进行更新调整，从而导致其收敛速度慢，且易陷入局部极小，因此难以满足控制系统对实时性的要求。相对于BP网络来说，RBF只需要对网络的部分权值进行实时调整，其具有算法复杂度低、所需运行时间短等优点，且能够规避BP网络易陷于局部极小的问题，因而在控制领域中得到了广泛的应用。

多输入单输出的RBF网络结构如图5所示。

图5 多输入单输出的RBF网络结构

对于任意的未知连续单值函数可以采用该神经网络对其进行拟合和逼近，具体形式如下：

(20)

f=W*Th(x)+ε

(21)

其中：W*为理想的权值矩阵，h(x)为径向基向量，ε为神经网络的逼近误差，x为神经网络网络的输入，cj为隐含层神经单元的中心点矢量，bj为径向基宽度，且满足bj> 0。

将上述的RBF神经网络用于估计无人艇模型中不确定性参数，定义函数

(22)

则根据RBF神经网络可以得到

(23)

其中：神经网络的输入为x=[u，v，r]T。

不确定项fu和fr的实际观测值为

(24)

2.4 自适应滑模控制器设计

滑模控制也叫做变结构控制，是一种特殊类型的非线性控制算法，因其具有鲁棒性强、响应迅速等优点，被广泛应用于干扰因素较多的无人艇运动控制中。滑模控制的基本思想是根据系统的数学模型和期望的动态性能设计一个滑模面，通过滑模控制器使系统状态可以从任意位置迅速收敛至滑模面附近。而当系统的状态接近滑模面后再采用切换控制以保证系统沿着滑模面收敛至原点。由于系统的动态特性只取决于设计的滑模面和滑模控制器，而与外界干扰无关，因而滑模控制系统对外部扰动和系统的不确定性有极强的不敏感性。

现将自适应滑模控制算法应用到所设计的欠驱动无人艇轨迹跟踪控制系统中。首先，定义前进速度和航向角的跟踪误差分别为

ue=u-up，ψe=ψ-ψp

(25)

构建如下两个滑模面：

(26)

其中：λ1，λ2为设计参数，且满足λ1，λ2> 0。

对式(26)进行求导可得

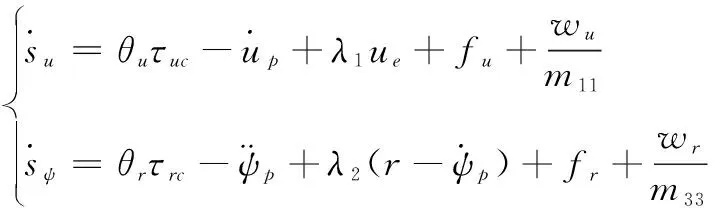
(27)

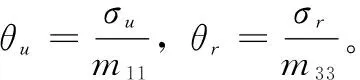
注意到上式中存在变量up和ψp的导数，而直接对up和ψp进行求导较为困难，且会出现微分爆炸的问题。为解决该问题，参考文献[20]中的方法，对变量up设计如下结构的微分观测器

(28)

其中：zu=[zu，1，zu，2，zu，3]T是微分器的状态变量，ku=[ku，1，ku，2，ku，3]T为微分器增益，并且满足式(29)中的矩阵Au为Hurwitz矩阵，βu，i∈(0，1)且βu，i=iβu-(i-1)，βu∈(0，1)，i=1，2，3。

(29)

au=kusu+ηusat(su)+WuThu(x) +

(30)

ar=krsr+ηrsat(sr)+WrThr(x) +

(31)

其中：ku，ηu，kr，ηr为设计参数，且满足ku，ηu，kr，ηr>0。sat(x)为饱和函数，采用饱和函数替代传统滑模控制中的符号函数进行切换控制，可以有效地抑制滑模控制中的抖振现象，其表达式为

(32)

选取自适应控制律为

(33)

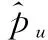
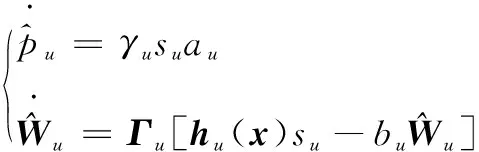
(34)

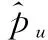
构造Lyapunov函数

(35)

将au的表达式代入，可以得到

(36)

构造Lyapunov函数

(37)

同理可得

(38)

2.5 稳定性分析

构造如下的Lyapunov函数

V=V1+V2+V3+V4

(39)

对式(39)进行求导并结合式(10)、式(17)、式(36)和式(38)，可以得到

(40)

根据Young’s不等式，有

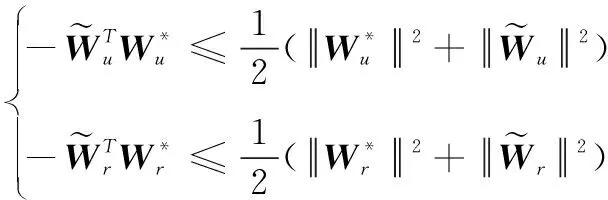
(41)

(42)

式(42)可以表示为如下的形式：

(43)

其中：

(44)

(45)

3 仿真结果与分析

为了验证所设计的欠驱动水面艇轨迹跟踪控制律的有效性和鲁棒性，采用MATLAB对控制系统进行仿真，并将仿真结果与文献[18]中的LOS-反步法和文献[21]中的反步滑模控制算法在相同的仿真环境和条件下进行了比较。仿真中采用的无人艇模型参数为m11=215±5，m22=265±5，m33=80±2，d11=170±3.5，d22=300±5，d33=50±1，无人艇的期望轨迹表达式为

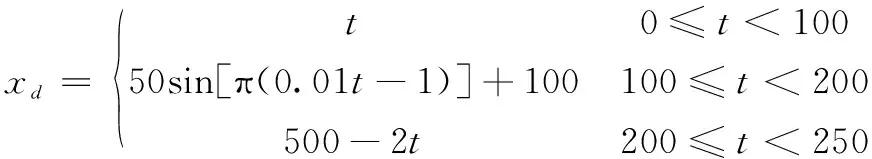
(46)

(47)

无人艇受到的外界风浪流干扰为

(48)

仿真中无人艇的执行器在150 s到250 s时发生了衰减故障，此时执行器的实际输出如式(49)所示，其余时间段内无人艇的执行器将正常运行。

(49)

图6 期望轨迹与实际轨迹

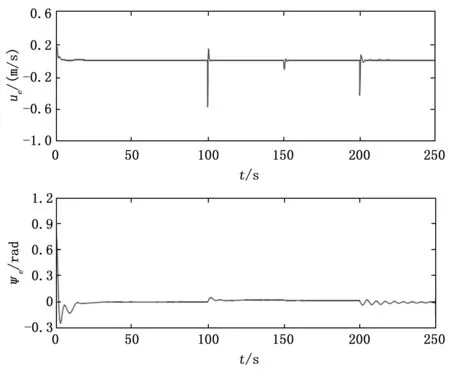
图7 前进速度和航向角误差

从图6中可以看出，在执行器衰减故障未发生时，文献[14]中的LOS-反步法和文献[17]中的反步滑模控制算法均可以在模型存在不确定性和外界存在风浪流干扰的条件下实现欠驱动无人艇的轨迹跟踪，但本文提出的控制算法的结果更加接近于期望轨迹。图8中的无人艇位置误差曲线的结果也佐证了这一点，且从中可以看出本文提出的控制算法相较于LOS-反步法和反步滑模法而言位置跟踪误差收敛更快，控制系统可以更早地到达稳定状态。表1为20～150 s时3种控制算法的平均跟踪误差表。此时，3种控制算法都已经进入稳定状态，且执行器未发生故障。从该表中可以看出，本文的算法的跟踪精度相较于另外两种对比算法提高了80%以上。图11中的干扰估计曲线存在明显的尖刺和扰动，这是由于模型参数不确定性导致的结果。虽然干扰的估计值存在着一定的误差，但在RBF神经网络的动态补偿下其估计值仍然与实际值基本保持一致，这说明了本文设计的非线性扰动观测器可以有效地估计外界的干扰并对系统补偿，从而提高了系统的鲁棒性。

表1 20～150 s跟踪误差平均值

图8 无人艇的横向误差、纵向误差与位置误差

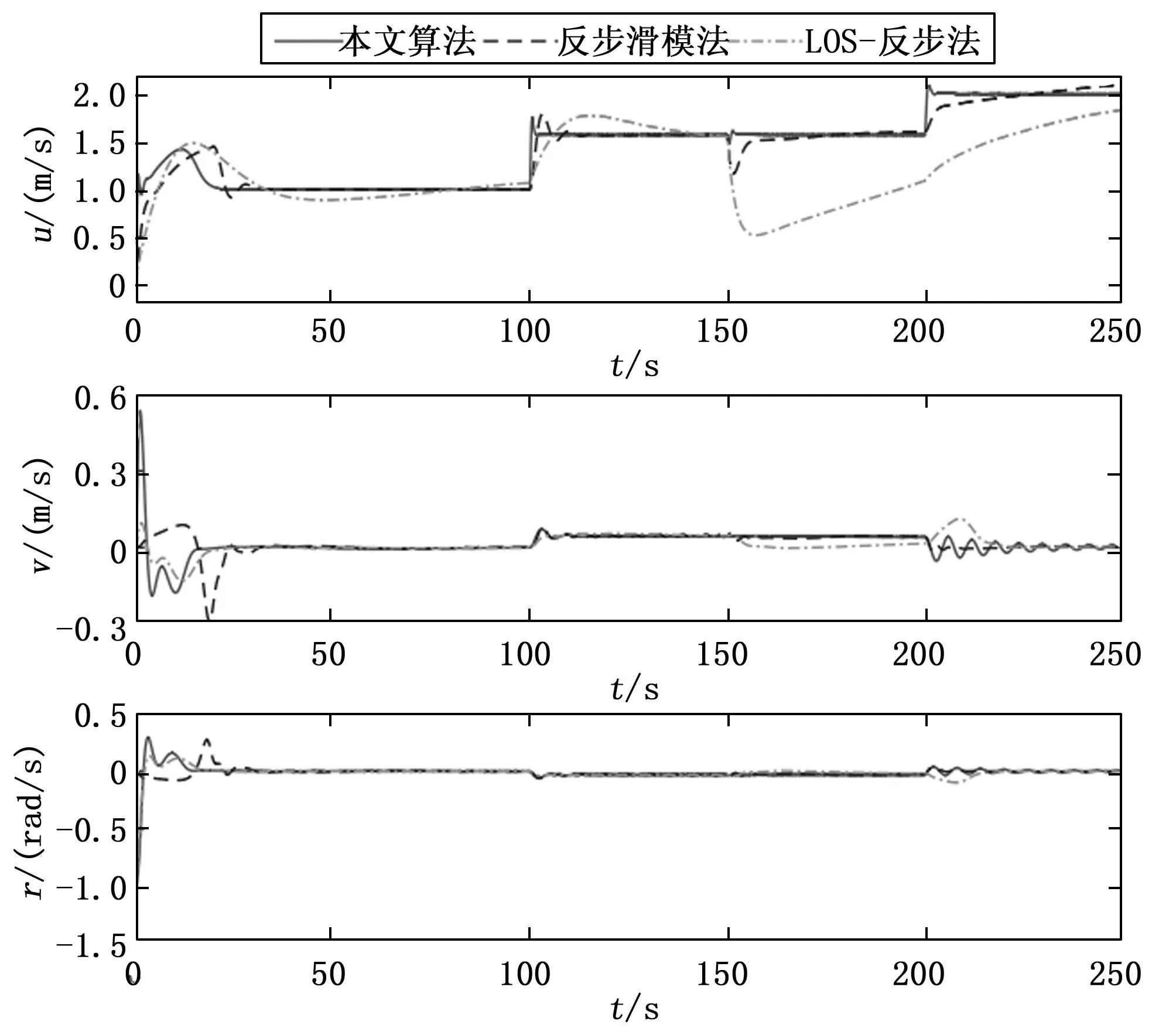
图9 无人艇的实际速度

图10 无人艇执行器的实际控制量

图11 外界干扰及其估计

在t=150 s后，无人艇的执行器发生了衰减故障。从图10中可以看到，在衰减故障的发生节点t=150 s处，系统的实际控制量存在着跳动，但很快就恢复正常，执行器的衰减故障对控制系统的实际影响较小。这说明了在执行器发生衰减故障的条件下，所设计的RBF神经网络和自适应控制律可以较好地抑制执行器故障所带来的影响，使无人艇轨迹跟踪系统具有一定的抗干扰和容错能力。而与之相比，采用LOS-反步法和反步滑模算法的无人艇则受到了明显的影响。从图6～9和表2中可以看到，在执行器发生故障后，采用反步滑模法的无人艇的位置跟踪误差明显增大，且纵向误差xe一直保持在2.5 m左右，无人艇的位置明显滞后于期望轨迹；而采用LOS-反步法的无人艇则出现了较为明显的失控现象，无人艇的运动轨迹与期望轨迹出现了明显的偏离。由此可见，本文提出的算法可以在外界干扰未知、模型参数存在不确定性和执行器可能出现衰减故障等较为复杂的环境条件下执行欠驱动无人艇的轨迹跟踪控制任务，且算法的调节时间较短、稳定性能良好，速度和位置误差的变化较为平滑，不存在较大的抖振和波动，具有良好的综合性能。

表2 150～250 s跟踪误差平均值

4 结束语

本文研究了欠驱动水面无人艇在模型参数不确定、外界存在未知时变干扰和执行器存在衰减故障等情况下的轨迹跟踪控制问题，提出了一种自适应滑模控制算法，并采用Lyapunov稳定性理论证明了控制系统的稳定性。与传统的轨迹跟踪控制策略相比，所提出的方法采用了非线性扰动观测器和RBF神经网络分别对无人艇受到的外界干扰和参数不确定项进行实时补偿，同时将无人艇的轨迹跟踪控制问题分解成了制导系统设计和动力学控制器设计两大部分，并在视线制导律的基础上提出了一种新的轨迹跟踪制导律，避免了直接采用反步法设计带来的困难。通过MATLAB对控制系统进行了仿真并与传统算法进行了比较；仿真结果表明，所提出的轨迹跟踪控制算法可以在较为复杂的环境下实现对欠驱动无人艇的精准控制，平均位置跟踪误差减小了80%以上，这说明了本文提出算法的有效性、稳定性以及鲁棒性。