基于实车试验的大跨度桥梁轨道静态长波高低不平顺验收标准验证

李国龙，孙宪夫，高彦嵩，杨 飞，高芒芒，柯在田

(1.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；2.中国国家铁路集团有限公司 科技和信息化部，北京 100844)

截至2022年底,我国高速铁路运营里程已超过4.2万km,并先后规划或投入运营了诸多设计速度为250 km/h且主跨达到千米级的公铁两用桥梁。其中主跨为1 092 m的五峰山公铁两用悬索桥[1]和沪苏通公铁两用斜拉桥[2]已建成通车;主跨为1 488 m的西堠门大桥[3]、正在研究的主跨为1 780 m的盐泰锡常宜铁路江阴长江大桥[4]则采用斜拉-悬索协作体系。铁路桥梁跨度增大,在列车荷载和环境作用下会引起桥梁更显著的挠曲变形及结构应力,还会带来桥上轨道平顺性的问题,在静动态验收和正常服役阶段,桥梁处于温度、风及列车荷载的组合作用下,结构变形和轨道形位与基准温度下的理想状态相差甚远[5]。

保持轨道线路的高平顺性和高稳定性是列车高速安全平稳运行的重要支撑[6-12]。轨道静态铺设精度也是轨道静态不平顺验收标准[13],大跨度桥梁轨道静态高低不平顺指轨道高程偏差,即不包含有桥上纵断面和桥梁温度变形的轨道不平顺。TB 10621—2014《高速铁路设计规范》[13]中规定对高低和轨向在采用10 m中点弦控制标准的基础上,增加了300 m(或480 a) 矢距差法长波控制标准,保证乘车的舒适性,但此方法主要适用于稳定的路基和简支梁桥等区段,对大跨度铁路桥梁而言,验收阶段桥梁线形由于施工偏差、二期恒载偏差及温度等因素影响,成桥线形与设计线形存在较大差异[14],且尚缺乏成桥线形与设计线形偏差标准,造成矢距差法不适用于大跨度桥梁轨道线形验收,尤其是桥上轨道高低长波不平顺评价结果严重超过标准限值。

赵文博等[15]发现在路基沉降区域轨道不平顺的300 m基线与车体加速度响应匹配性较差,在目前的验收管理限值下并不适用于直接对运营期高速铁路长波不平顺进行评价。近几年基于中点弦测法与车辆动力响应关系研究提出的60 m弦测法控制标准也广泛用在了既有高铁提速和大跨度铁路桥梁桥上轨道平顺性静态验收中[16]。杨飞等[10]基于实测轨道不平顺和车体加速度响应关系,针对运营期高速铁路轨道长波不平顺,提出不同速度条件下的60 m弦控制标准,并在京津城际达速中开展应用[7]。

本文在总结前期研究成果基础上,首先,针对设计速度为250 km/h的高速铁路有砟轨道大跨度桥梁,基于综合检测列车实测数据,通过分析轨道高低不平顺不同弦长与车体垂向振动加速度之间的关系,选取速度为250 km/h高速铁路有砟轨道静态长波高低不平顺合理的评价弦长;其次,基于统计分析,提出评价弦长幅值与车体垂向振动加速度之间的关联关系,依据线路验收阶段对车体加速度的限值要求,提出了速度为250 km/h高速铁路有砟轨道大跨度桥梁静态高低长波不平顺验收限值建议,最后通过在某设计速度为250 km/h且主跨为672 m高速铁路有砟轨道斜拉桥上预设轨道高低不平顺的实车验证,验证了大跨度桥梁静态高低长波不平顺验收限值的合理性。

1 大跨度桥梁轨道静态长波高低不平顺验收标准

1.1 大跨度铁路桥梁验收现状

超大跨度铁路桥梁在验收阶段由于施工偏差和环境等多因素影响下,成桥线形与设计线形差异显著[16],同时,成桥线形与设计线形偏差限值尚无相关标准,因此,只能通过轨道静态不平顺来评价桥梁整体线形情况,而有砟道床可调整量无法使轨道静态长波不平顺满足现行轨道静态长波不平顺验收标准,因此,亟需研究确定大跨度桥梁区段轨道静态不平顺验收标准限值。

现行TB 10754—2018《高速铁路轨道工程施工质量验收标准》[17]中对轨道静态高低长波不平顺的验收标准采用30 m(5 m)基线限值2 mm(基线长30 m,每5 m矢距差限值为2 mm,下同)以及300 m(150 m)基线限值10 mm(基线长300 m,每150 m矢距差限值为10 mm,下同)进行卡控。

沪苏通长江公铁大桥和五峰山长江大桥原始铺轨线形高低静态不平顺无法满足30 m(5 m)基线限值 2 mm以及300 m(150 m)基线限值10 mm的限值要求,之后调整了桥上线路设计纵断面,但调整后的五峰山长江大桥线路纵断面最小坡段长度突破了600 m,且轨道高低长波静态不平顺仍不满足基线限值的要求,目前有多座主跨超600 m甚至超千米级的大跨度铁路桥梁投入运营和开工建设,目前的桥梁和桥上轨道静态验收标准存在局限性,建议根据轨道不平顺和行车性能重新研究制定。

1.2 中点弦测法

中点弦测法示意见图1。

图1 中点弦测法示意

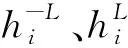
(1)

式中:i为沿轨道方向坐标。

对式( 1 )作傅里叶变换,可得

(2)

(3)

式中:ω为空间角频率,rad/m;ω=2π/λ,λ为轨道不平顺波长,m;L为1/2弦长,m;H(ω)为传递函数。

由式( 3 )可知,弦测法传递函数H(ω)随着ω的变化在0～2区间变化,不同弦长有效测量波长范围不同,见图2,为确保检测到有效波长,应当采用不同的检测弦长[10],并涵盖车辆的敏感波长,不同增益系数下的部分弦长和波长对应关系见表1。

图2 不同弦长控制的有效波长范围

表1 敏感波长分析表

根据文献[10]中对综合检测列车敏感波长和不同弦长与车体垂向振动加速度之间的密切关系可知,速度为250 km/h高速列车垂向敏感波长为53～61 m,且在增益系数在1.0情况下,60 m中点弦测法的有效测量波长范围为40～120 m,可以覆盖列车的敏感波长,同时文献[10]中也阐明了车体垂向振动加速度与60 m中点弦测值之间存在强相关性,因此,为保证全线标准的一致性和现场可操作性,本文亦采用60 m中点弦测法对大跨度桥梁轨道静态长波高低不平顺进行验收。

收集综合检测列车在速度为250 km/h下近200组路基直线区段(包含部分竖曲线设置区段,每组线路长500～1 000 m)轨道动态长波高低不平顺和对应的车体垂向振动加速度实测数据,将轨道高低不平顺计算完弦测值后按照间隔1 mm进行分组,并对每组轨道不平顺所对应的车体加速度进行统计分析,为去除轨枕空吊、结构病害等对不平顺和车体加速度的影响,首先计算车体加速度的平均值和标准差,然后计算95%置信度条件下的最大值。最后以每组数据的轨道不平顺60 m弦测值的均值为横坐标、95%置信度车体加速度为纵坐标进行拟合[18],得出车体加速度与高低不平顺60 m弦测值之间基本呈线性关联关系,见图3。

图3 轨道高低不平顺60 m弦中点弦测值与车体垂向振动加速度之间的关系曲线

车体垂向振动加速度a与不平顺的60 m弦测值之间的关系为

a=0.006 3x+0.02

(4)

式中:x为轨道不平顺的60 m弦测值,mm。

由于大跨度桥梁跨中设置圆曲线型竖曲线,对于设计速度为250 km/h的高速铁路桥梁最小竖曲线半径为20 000 m,根据式( 5 ),对车体产生的离心加速度为0.024g,五峰山长江大桥、鳊鱼洲长江大桥和常泰长江大桥[19]等竖曲线半径为25 000 m,对应的离心加速度为0.019g。由竖曲线产生的车体垂向振动加速度ac表达式为

(5)

式中:v为列车行进速度,km/h;R为圆曲线半径,m。

TB 10761—2013《高速铁路工程动态验收技术规范》[20]中规定新线在验收阶段引起的车体垂向振动加速度动态限值为0.1g,由式( 4 )可知,对于设计速度为250 km/h的大跨度铁路桥梁,最小的竖曲线半径、实际设置竖曲线半径和不考虑竖曲线对车体垂向振动加速度的影响的轨道高低不平顺60 m弦测值分别为8.89、9.5、12.7 mm,即介于8～12 mm之间,扣除竖曲线的影响后,暂定为10 mm。

2 验收标准的实车试验验证

为了验证速度为250 km/h高速铁路大跨度桥梁轨道验收标准的合理性,于2021年11月25日—2021年11月30日,在某主跨为672 m的钢箱混凝土混合梁斜拉桥跨中预设轨道静态高低不平顺,开展60 m弦轨道静态长波高低不平顺偏差实车试验。

2.1 预设不平顺设置

斜拉桥方案设置见图4。图4中,孔跨布置为(2×50+224+672+174+3×50) m,其中主、辅跨设计为钢箱梁,锚跨设计为预应力混凝土箱梁,主跨跨中72 m范围内斜拉索交叉设置。纵向以主跨中心为对称点设3‰的人字坡,竖曲线半径为25 000 m。

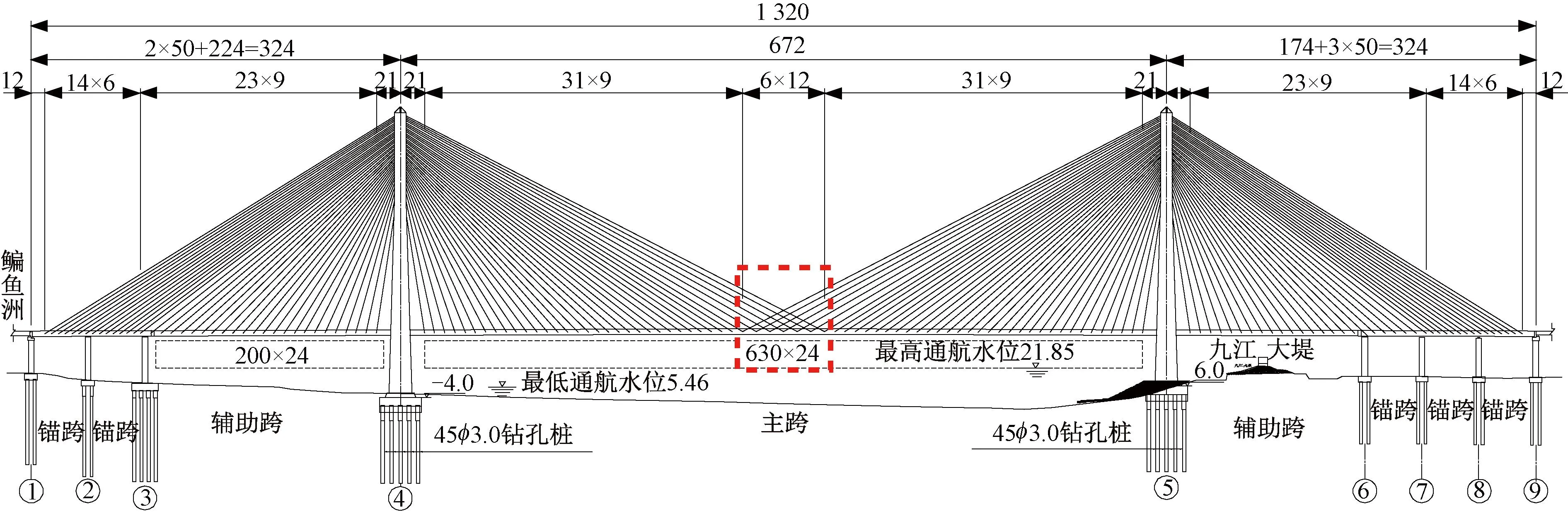
图4 主桥方案设置(单位:m)

根据文献[10]中对综合检测列车敏感波长特征分析,且考虑不同型号综合检测列车之间存在差异,基于现场可操作性,采用波长为60 m的连续余弦波形式布置,即以主跨跨中为对称点,左右各90 m范围内布置3个余弦波,波长60 m,峰-峰值10 mm(60 m中点弦测值为10 mm),两侧各顺延半个波长,最终形成“四峰三谷”的效果,多波形式可更好地保证列车的振动稳定性,预设不平顺范围全长为240 m,不平顺设置后的理想效果如图5黑线所示,轨枕间距为0.63 m,按0.5 mm厚度的垫板进行调整,每个扣件位置处垫板理论调高量如图5中红点所示。根据不平顺设置方案,左、右钢轨同等设置高低不平顺,且不改变轨向、轨距等项目。

图5 60 m波长余弦波不平顺设置方案及扣件调整量

2.2 预设不平顺效果

轨道静态高低不平顺设置完成后,分别于27日中午(环境温度17 ℃)和傍晚(13 ℃)采用轨测仪和水准仪进行轨面高程测量,29日预设不平顺拆除后,于当日下午(14 ℃)对桥上轨面高程进行测量,实测轨面高程和基准环境温度(20 ℃)下的轨面高程见图6。由于桥梁施工偏差和二期恒载的差异,造成相同温度下,实际轨面高程较设计轨面高程偏低。大跨度桥梁温度变形较为显著,且梁轨相互作用关系复杂,整体表现为桥面高程与温度成反相关关系,且由轨面高程偏差可知,桥面高程变化约为5 mm/℃,如图7所示,从高程偏差曲线中可以明显看到在跨中存在“四峰三谷”形式的高低不平顺,即为大跨度桥梁轨道高低不平顺曲线,还可得知不同温度下高程偏差存在差异,但整体表现出[10]由于桥梁温度变形造成的长波差异,波长可达370 m。对高低不平顺计算60 m中点弦测值,计算结果见图8,由于中点弦测法的特性,如图2不同弦长控制的有效波长范围可知,选用60 m中点弦时,200 m及以上波长的增益系数不到0.5,300 m及以上波长的增益系数则更低,不足0.25,即60 m中点弦测值可以将因桥梁温度变形产生的长波差异大部分过滤掉,也可以更准确的提取出对行车性能有影响的波长成分,便于对轨道不平顺进行评价。提取出波峰和波谷对应的60 m弦测值,除第三个波峰未达到9 mm外,其他波峰和波谷位置均达到了9～11 mm范围内,最小为8.68 mm,位于第三个波峰,最大为10.79 mm,位于第二个波峰位置,具体见表2,两种测量设备计算的60 m中点弦测值相差较小,总体预设不平顺效果较好,达到试验预期目标。

表2 波峰、波谷60 m中点弦测值统计表 mm

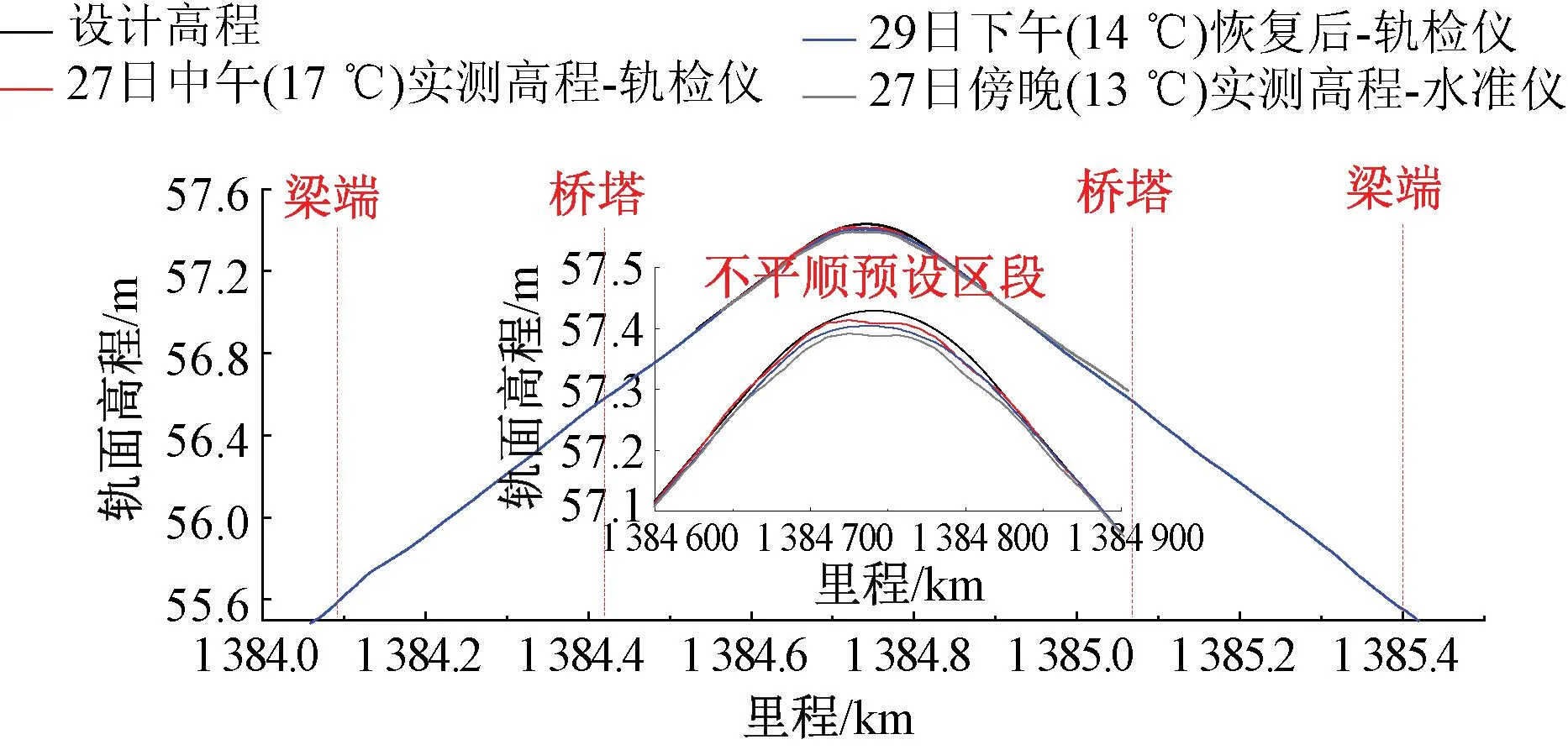
图6 桥上轨面高程曲线

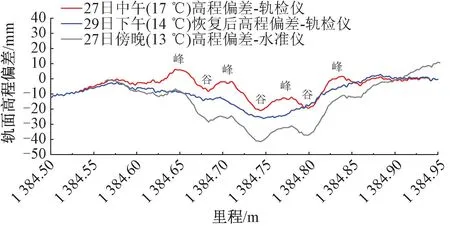
图7 轨面高程偏差曲线

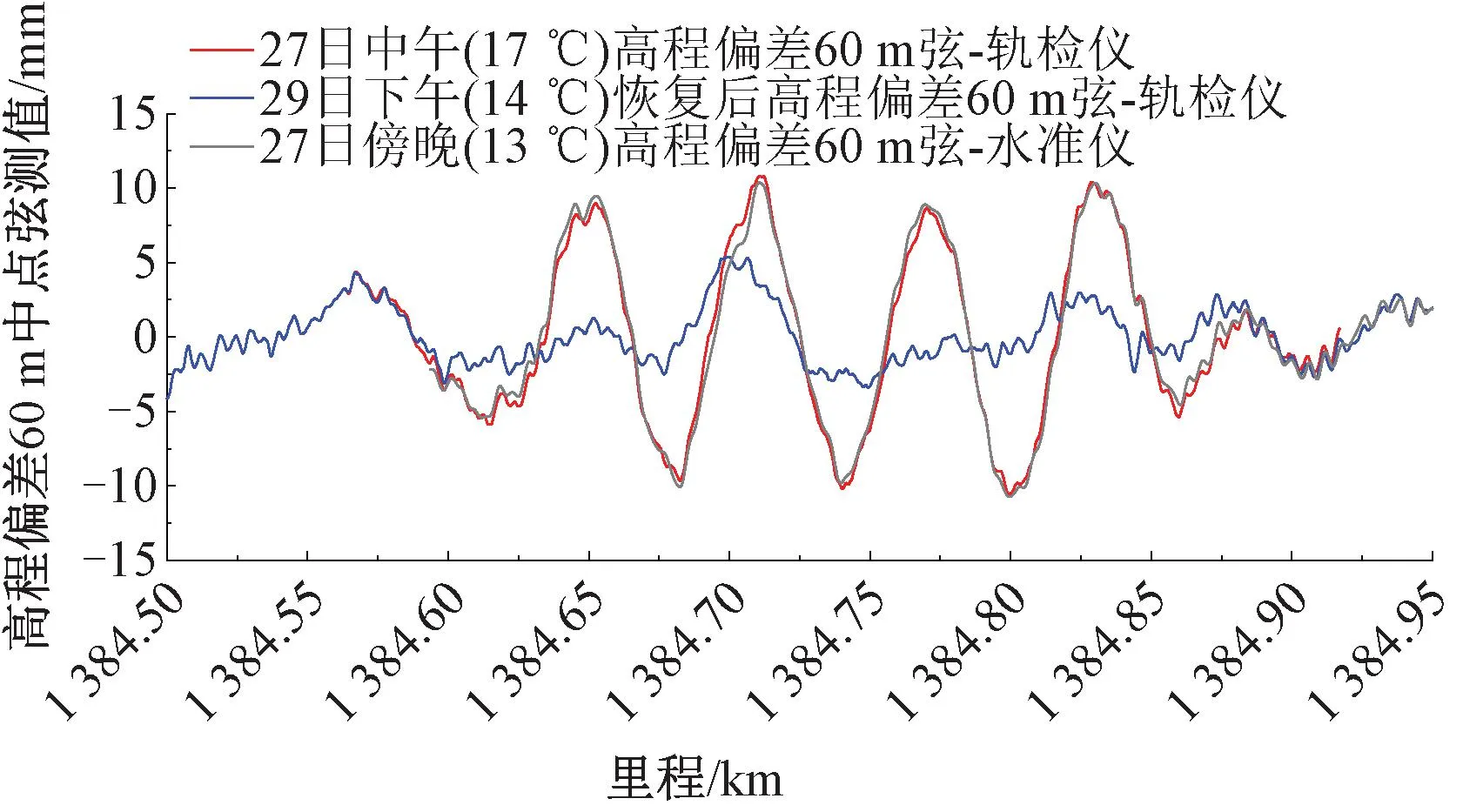
图8 轨面高程偏差60 m中点弦测值

轨面高程偏差30 m基线(5 m)及300 m基线(150 m)矢距差分别见图9、图10。由图9和图10可知,对恢复预设不平顺后跨中区域轨面高程偏差分别计算30 m基线(5 m)和300 m基线(150 m)矢距差,其最大值分别为2.52、23.53 mm,均超过对应限值2 mm和10 mm的要求。

图9 轨面高程偏差30 m基线(5 m)矢距差

图10 轨面高程偏差300 m基线(150 m)矢距差

3 车辆动力响应分析

通过采用综合检测列车CRH380AJ于白天和夜间不同时间段开展实车试验,测试车体振动加速度和轮轨力数据,验证实设不平顺和不同速度工况下的动力学性能。

2021年11月27日按最低温度时段(22:00—03:00,温度范围为11.43～12.53 ℃)至28日最高温度时段(11:00—16:00,温度范围为14.61～18.56 ℃)开展了逐级提速检测,包括180、200、220、240、250、260、270、275 km/h共8个速度级,且当列车速度为250 km/h时,夜间和白天桥梁跨中区域环境温度分别为12.01、16.74 ℃。

3.1 行车舒适性分析

列车正、反向行驶通过桥梁区段,正向通过测试头车车体垂向振动加速度,反向通过则测试尾车车体垂向振动加速度。27日夜间和28日白天测试的车体垂向振动加速度时程曲线见图11和图12(图例中Z代表正向,F代表反向),由图11和图12可知,列车以不同速度经过预设不平顺区段,均激起了车体的周期性振动,且车体垂向振动加速度随着列车速度的提高不断增大,正、反向通过时,由于列车的环境振动特性不同,车体垂向振动加速度略有差异,但整体差异较小。

图11 27日夜间车体垂向振动加速度时程曲线

图12 28日白天车体垂向振动加速度时程曲线

列车正向经过预设不平顺时,当列车速度为250 km/h,夜间和白天车体垂向振动加速度最大分别为0.87、0.85 m/s2,均不超过1.0 m/s2限值标准,Sperling指标分别为2.47、2.43,舒适性评价均为“优秀”,接近优秀/良好分界线(2.5);列车速度为270 km/h时,夜间和白天车体垂向振动加速度最大分别为0.98、0.97 m/s2,Sperling指标分别为2.47、2.42,舒适性评价均为“优秀”;列车速度为275 km/h时,夜间和白天车体垂向振动加速度最大分别为0.92、0.91 m/s2,Sperling指标分别为2.48、2.42,接近优秀/良好分界线(2.5),列车正向通过时的车体垂向振动加速度最大值统计结果见表3。由表3可知,当列车速度为270 km/h时的车体垂向振动加速度达到最大值,接近车体的共振速度。

表3 车体垂向振动加速度最大值统计表 (正向)

夜间和白天引起的车体垂向振动加速度无明显差异。

列车正向经过波峰和波谷位置时激起的车体垂向振动加速度最大值见表4。由表4可知,列车在经过第二、三个波峰位置时产生的车体垂向振动加速度明显大于其他位置,即桥梁跨中圆曲线型纵断面对车体垂向振动产生了一定的影响。同时为了验证式( 4 )的合理性,将波峰、波谷处两种测量设备的60 m弦测最大值代入式( 4 ),将理论计算和250 km/h实测的车体垂向振动加速度见表5。由表5可知,理论计算的车体垂向振动加速度与实测值吻合较好,且略有偏大,在实际使用过程中,基于车体垂向振动加速度推导轨道不平顺管理限值偏于安全。

表4 波峰、波谷位置处车体垂向振动加速度a最大值统计表(正向) m·s-2

表5 波峰、波谷处理论与实测车体垂向振动加速度

综合分析车体垂向振动加速度,正向通过预设不平顺区段,当列车速度为250 km/h时,夜间和白天车体垂向振动加速度最大分别为0.87、0.85 m/s2;夜间和白天列车以速度为275 km/h经过试验区段时的车体垂向振动加速度最大分别为0.92、0.94 m/s2;车体垂向振动加速度最大值为0.98 m/s2,既满足TB 10621—2014《高速铁路设计规范》[13]1.3 m/s2的限值标准,也满足TB 10761—2013《高速铁路工程动态验收技术规范》[20]1.0 m/s2的限值标准。舒适性指标最大为2.47,评价为“优秀”,接近优秀/良好分界线(2.5)。

3.2 行车安全性分析

通过动车组动力学响应测试,根据GB 5599—2019《机车车辆动力学性能评定及试验鉴定规范》[21]中相关要求,获取脱轨系数、轮重减载率和轮轨力等评价列车运行安全性指标,详细数据见表6,由表6可知,预设高低不平顺属于长波成分,主要影响列车的垂向振动加速度响应,对脱轨系数、轮重减载率等安全性指标影响较小,列车经过预设不平顺区段时脱轨系数最大为0.09,轮重减载率最大为0.16,轮轴横向力最大为10.4 kN,构架横向加速度最大为2.6 m/s2,轮轨垂向力最大为96.5 kN,均在安全范围内,且安全冗余显著。

表6 列车运行安全性评价指标

4 结论

本文首先基于大量的轨道几何不平顺和车体垂向振动加速度实测数据,提出了车体加速度与不平顺的60 m弦测值之间的关系,其次结合桥梁纵断面对行车的影响,给出高速铁路有砟轨道大跨度铁路桥梁轨道不平顺验收标准建议,最后通过开展实车试验进行了验证,主要结论如下:

1)设计速度为250 km/h的高速铁路有砟轨道大跨度桥梁轨道静态长波高低不平顺验收限值采用60 m弦中点弦测值10 mm是合理可行的。

2)对于速度为250 km/h的高速铁路,车体垂向振动加速度a与不平顺60 m弦测值x之间的关系为:a=0.006 3x+0.02。

3)大跨度桥梁温度变形较为显著,整体表现为桥面高程与温度成反相关关系,除跨中设置圆曲线型竖曲线对车体垂向振动加速度存在一定影响外,桥梁由于当日温差产生的变形属于长波成分,对行车基本无影响。

4)车体垂向振动加速度随列车速度的提高而增大;列车正向通过预设不平顺区段,速度为250 km/h时,车体垂向振动加速度最大为0.87 m/s2,舒适性指标为2.47,评价为“优秀”,且接近优秀/良好分界线(2.5)。列车速度在275 km/h及以下,产生的车体垂向振动加速度最大值为0.98 m/s2,既满足TB 10621—2014《高速铁路设计规范》[13]1.3 m/s2的限值标准,也满足《高速铁路工程动态验收技术规范》[20]1.0 m/s2的限值标准,舒适性指标最大为2.47,评价为“优秀”,接近优秀/良好分界线。

5)实车试验表明,预设高低不平顺属于长波成分,主要影响列车的垂向振动加速度响应,对行车安全性影响较小。