面向山区铁路工程物流基地选址的分布鲁棒优化模型

王 浩，甘 蜜，魏力飞，何 庆，王 平，彭 涛，3

(1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 交通运输与物流学院，四川 成都 610031；3.江苏省现代城市交通技术江苏高校协同创新中心，江苏 南京 211189)

《“十四五”现代综合交通运输体系发展规划》明确指出要完善综合运输大通道,加强出疆入藏、中西部地区、沿江沿海演变战略骨干通道建设工程。这些通道建设多位于山区,沿线地形起伏剧烈、地质条件复杂、潜在地质灾害风险高[1],且地广人稀、居民分布离散,既有交通道路资源薄弱、路网密度低、抗自然灾害能力弱,不足以支撑铁路大型工程开展。在此基础上,选取合适的物流基地节点,形成配套运输通道,对保障大型铁路工程物资需求准时运达、改善沿线交通设施条件、促进地区经济社会发展具有重要意义。

选址问题在城市规划、建筑设计、工程建设等领域具有重要意义,其合理性与成功性直接关系到后续的发展和建设,因此国内外针对选址问题的研究众多。现有铁路工程建设配套设施基地选址解决方案主要可以分为两类,一类是建立选址规划数学模型,求解得到选址决策方案。吕春妍等[2]认为选址与铁路项目的成本、工期、安全性、环境影响程度存在耦合关系,构建土方调配及弃土场选址协同优化模型并利用粒子群算法进行求解。吕红霞等[3]综合考虑场地建设可行性、场地建设成本等相关因素,提出铁路隧道相邻紧急救援站最大设置距离计算方法,建立紧急救援站选址模型,设计启发式算法进行求解,从而确定最终的救援备选点数量和地点。彭丹阳[4]针对铁路运用物资区域联合储备中心建设的经济性、适用性、时效性及协调性要求,构建物资供应时间的满意程度函数,通过数学规划模型与K-Means聚类确定最终选址。另一类通过构建选址相关影响因素评价指标,通过层次分析、模糊综合评价等方法确定选址节点。林家琛[5]考虑高速铁路铺轨基地方案技术指标、经济环境效益指标、未来运营等因素构建了基于TOPSIS的铺轨基地选址方案。部分学者[6-9]聚焦于贮存特点要求更为不同的铁路应急物资规划与物资储备上。张锦等[10]将应急物资概念引入铁路工程建设中,采用三角模糊数刻画不确定参数,构建了基于多场景的两阶段模糊非线性选址-路径模型。

不难看出,针对铁路工程特点和工程所需配套设施基地的建设特点,现有铁路工程建设配套设施基地节点选址研究对不同选址影响因素有所侧重[16-17]。而现有研究通常假定该类配套设施基地在铁路工程落成后即拆除或全部作为永久设施留用,对配套设施基地在未来的可利用性和工程建设整体经济性的考量不足,忽视了部分设施永久留用的规划建设模式。该模式通常被称为永临结合建设模式,通常分为工程结合和场址结合两种。此模式强调可持续性,综合考虑环境、社会和经济因素。在铁路工程配套设施选址中考虑永临结合,能有效促进资源集约利用,以及在可预见未来保障基础设施的灵活利用,从而实现长期的工程经济性和社会效益的平衡。

本文首先构建包含空间因素、经济因素、交通运输组织因素的山区铁路工程配套物流基地选址评价指标体系,确定各主要影响因素间的相对重要程度;然后引入永临结合决策变量,在保障工程物资运输需求的同时,选择部分物流基地节点留用,服务于未来山区经济发展与社会物流需求;为精确刻画社会物流需求的不确定性,进一步采用鲁棒优化方法,构建包含临时、长期物流基地点选取与拆除、运输计划指定的物流基地点选址优化的两阶段混合整数规划模型,结合模型特点推导出可计算的等价形式;最后,通过实际案例分析不同因素变动对选址方案的影响,为添加未来可持续发展利用考量的铁路工程配套运输物流基地节点选址提供决策参考。

1 问题描述

山区的配套道路网络优化需要考虑当前的工程物流需求和未来的社会需求分布,从而获取山区物流网络结构,具体供应链网络示意见图1。在此基础上,考虑施工点的地质结构和空间格局对各施工点进行特征分析,并基于网络拓扑性质选取候选物流基地,最后利用通道优化模型选取“永临结合”下的运输通道方案。本文主要解决以下问题:①临时物流基地的选取;②针对未来社会需求的长期物流基地选取;③供应商到物流基地再到施工点的运输计划。

图1 供应链网络示意

此问题可以描述为一个两阶段模型:①考虑当前施工中工程物流需求的临时物流基地布局优化和分配问题;②考虑修缮完成后,将临时物流基地改善成长期物流基地为社会需求服务,而未被选取的临时物流基地将进行拆除。

综上所述,根据施工实际情况,本文做出以下假设:

1)临时物流基地的备选点经过建设工程现场调研确定。

2)物流基地和施工点之间不能进行运输。

3)每个施工点有且只有一个物流基地为其运输。

4)物流基地到施工点之间的运输一定能够完成。

2 方法

2.1 评价指标

不同于一般地质条件下的物流基地选址,山区地质构造极其复杂,具有敏感脆弱的生态环境,因此,需要构建一套山区物流基地选址评价指标体系,对通道优化中的选址外生成本进行评估,以增强优化结果的可行性。

1) 空间因素。选取地质条件稳定的空旷地带,有利于物流功能开展的地点,同时,选取到达其他节点都更为便捷的节点,有利于减少物流运输成本,同时需要远离自然灾害及动物迁徙,因此,采用工程地质条件指标衡量海拔和地质构造等因素。

2) 经济因素。不同物流基地点选址需要的建设成本不同,其地基、外体的建设以及内部仓储配备均需要资金,同时需要考虑在山区建设的土地征用和维护等,因此以修建成本、维护成本和土地成本指标代表经济状况方面的影响因素。

3) 交通运输组织因素在山区下的物流基地选址应考虑可达的服务范围以及真实的运输距离。因此,分别以服务半径和道路情况作为衡量指标。

结合以上分析,为保证物流基地设施发挥其设定的功能,建立山区物流基地选址评价指标体系,见表1。

表1 山区物流基地选址评价指标体系

根据已构建的山区物流基地选址评价指标体系,采用AHP方法对选址优化模型中各影响因素指标权重进行确定。由于山区物流基地选址问题涉及多个因素,如地质条件、经济成本因素等,而AHP方法能够有效地处理多因素的决策问题,并通过层次结构的方式将问题分解,使得问题更加可管理。为规避AHP方法中存在的主观性判断,在实际应用中,首先邀请在山区铁路工程选址修建领域具有丰富经验的专家,通过集体讨论和专家投票,获取更加客观和综合的判断,从而降低主观性的影响。然后,采用经典的AHP标度:1、3、5、7、9构建判断/比较矩阵。标度数字表示因素之间相对重要性的程度,有助于在判断矩阵中表达不同因素之间的差异;最后,采用一致性比率来评估专家判断的一致性。如果在构建判断矩阵时,专家的判断不够一致,将重新进行讨论并调整,以确保判断矩阵的一致性,从而提高权重指标的可靠性。

2.2 选址优化模型构建

模型变量及说明见表2。

表2 变量及说明

根据传统选址模型以及文献[11]中针对永临结合选址的二阶段模型的启发,本文以最小综合评价指标为目标函数,构建的二阶段确定性模型如下。

第一阶段:

(1)

xipdip≤ri∀i∈I∀p∈P

(2)

(3)

xip≤yi∀i∈I∀p∈P

(4)

(5)

(6)

(7)

第二阶段:

(8)

μqi≤θi∀i∈I∀q∈Q

(9)

(10)

θi+φi=yi∀i∈I

(11)

式( 1 )表示总的目标函数值,第一项为所选临时物流基地的综合评价值,第二项和第三项为运输成本,第四项为二阶段的总目标函数值。在第一阶段中,约束式( 2 )表示服务范围约束;约束式( 3 )～式( 5 )表示只有被选为临时物流基地才能接收供应商的物资并运输至施工点;约束式( 6 )表示物流基地的容量约束;约束式( 7 )表示施工点有且只有一个物流基地为其服务。

式( 8 )为第二阶段的目标函数值,第一项为所选长期物流基地的综合评价值,第二项为拆除成本,第三项为运输成本。在第二阶段中,约束式( 9 ) 表示只有被选为临时物流基地才能接收供应商的物资;约束式(10)表示供应商运输到长期物流基地的物资必须满足该物流基地所服务城市的社会需求;约束式(11)表示临时物流基地拆除或被选为长期物流基地。

2.3 鲁棒优化模型建立

在实际中,对未来城市的社会需求是无法精准预测的。同时由于各种非可控因素影响(山区道路状况,地质灾害等),实际的最大运输量无法获得精准数据,具有较大的不确定性。为了更好地表示这种不确定性,令

在波动变量的影响下,约束式( 9 )并不总是成立的,因此,其在一定概率下保持成立的不确定形式为

0}≥1-ε∀i∈I

(12)

式中:ε为容忍度水平。

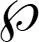
(13)

综上所述,当未来需求和最大运输量具有较大不确定性时,第二阶段模型可以改写为以下分布鲁棒优化模型

s.t.式( 9 )、式(11)、式(13)

2.4 非精确集机会约束处理

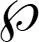
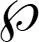
(14)

∀i∈I

(15)

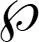
={ξ:‖ξ‖1≤Ω}

(16)

式中:Ω为波动集的上界。

为方便表述,将波动变量ξi简化为ξ=[ξk],k=1,2,…,|Q|+1,波动变量ξk对应的参数为zk。基于给出的波动集,可以通过以下定理得到式(15)的安全凸逼近形式。

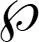
Ωmax|zk|+z0≤0

(17)

={ξ∈RK,Pξ+p∈L}

(18)

式中:Pξ=[ξ0],p=[0K×1Ω],并且L={[ξΩ]:‖ξ‖1≤Ω}是K+1维的劳伦斯锥,则其对偶锥L*={[ξΩ]:‖ξ‖∞≤Ω}。

因此可以得到鲁棒对等形式Ωmax|zk|+z0≤0。

②证明式(17)是非精确机会约束式(15)的安全凸逼近。以下等价表示显然成立。

(19)

因此当波动变量ξk∈[-1 1]且相互独立时有

(20)

通过柯西不等式可以得到

(21)

所以,有

(22)

基于文献[12],有

(23)

根据式(19)的等价表示,结论得证。

式(17)的任意可行解对式(15)都是可行的。因此可以将约束式(13)替换为约束式(17)的形式,来近似求解原分布式鲁棒优化模型。替换后新的第二阶段“多面体-DRO”模型为

(24)

(25)

s.t. 式( 9 )、式(11)

3 案例分析

首先,将对确定性的二阶段模型进行结果分析和敏感性分析。其次将其与分布式鲁棒优化模型在不同服务水平下的计算结果进行对比,据此来验证所提出的分布式鲁棒优化模型的有效性。所有的数据来源见3.1节,数值实验均在一台具有12 GB运行内存、处理器为Intel(R) Core(TM) i5-6300HQ 2.30 GHz的计算机上运行,使用Gurobi 9.1.1商业求解器进行求解。

3.1 数据介绍

根据调研,平原地区物流基地地区建设成本为750元/m2,土地出让的成交地面均价为8 000元/m2,砖混结构(±0.000以上)拆除单价为31元/m2。共有12个物流运输物流基地备选点,编号为i1～i12,备选点数据见表3。需求点为p1～p30,供应商为q1～qb,建设成本、土地征用成本根据高原地区人工机械降效情况、平原地区单位建设成本、平原地区维护成本、不同设防烈度土建成本等因素确定。短期维护成本、长期维护成本根据平原地区维护成本确定。拆除成本根据高原地区人工机械降效情况、平原地区砖混结构拆除单价确定。根据备选点所在不同海拔及地震动峰值加速度(地震烈度),对不同备选点对应的成本费用进行相应增幅。根据TZJ 3001—2017《铁路基本建设工程设计概(预)算费用定额》[13],将海拔高度划分为[0,2 000)、[2 000,3 000]、(3 000,4 000]、(4 000,4 500]、(4 500,5 000]、(5 000, +∞)6个等级,其费用增幅依次为 0%、20%、34%、54%、60%、90%[14]。不同防烈度土建成本根据地震动峰值加速度进行划分,其中0.05g～0.1g增幅为3.17%,0.1g～0.15g增幅为8.15%,0.15g～0.2g增幅为8.15%[15]。对于未来社会需求由以往城市社会需求量预测得到,社会需求预测量见表4,每个备选点的需求表示其作为长期物流基地所覆盖的所有城市的需求量总和。

表3 备选点数据

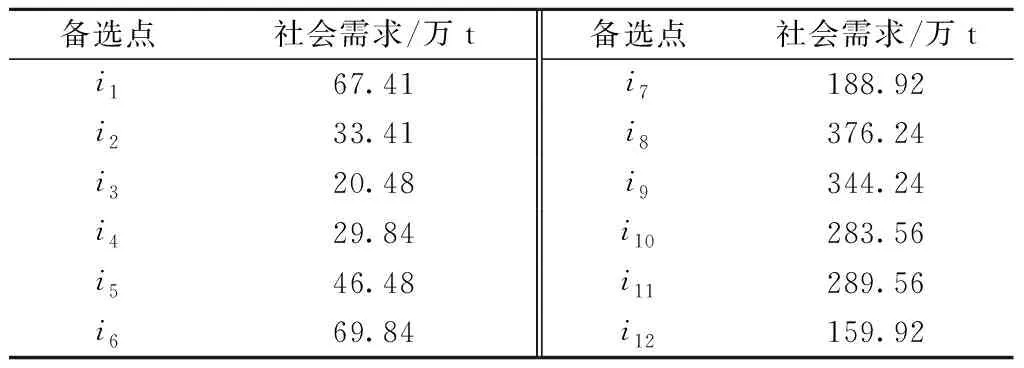
表4 社会需求预测量

根据供应商、备选点和施工需求点的实际线路情况,利用经纬度距离计算公式测量两点之间距离,从而获得供应商到备选点、备选点到施工需求点的距离矩阵。综上,选址场景中5个供应商、12个备选点以及40个施工需求点的空间分布见图2。

图2 空间分布

3.2 确定性模型结果分析

通过AHP方法计算得到第一阶段工程地质条件、建设成本、短期维护成本、土地征用成本、服务水平和道路情况6个因素的权重分别为0.342 4、0.207 5、0.036 1、0.062 2、0.191 4;第二阶段工程地质条件、长期维护成本、土地征用成本、拆除成本和道路情况5个因素的权重分别为0.345 7、0.181 2、0.204 1、0.206 9、0.062 2。

本文将临时物流基地的服务水平刻画为服务范围,即最大服务距离。最大服务距离依次分为40、60、80、100、120 km。在复杂山区的设施选址过程中,本文认为主要的影响因素应当是建设施工费用和工程地质条件,因此将探究在不同服务水平下,建设成本和工程地质条件的变动对最终结果的影响见图3,具体数值见表5。

表5 不同变动量的计算结果

图3 不同变动量的计算结果

由图3(a)可见,当服务水平不变时,目标函数与建设施工费用呈正比关系,总体变动为20.2%～28.8%;在同一建设成本下,目标函数随着服务水平提高而降低。由图3(b)可见,目标函数与工程地质条件呈正相关,但受工程地质条件的影响并没有建设成本的影响明显,变动仅仅只有1.3%～8.7%;在工程地质条件一定的情况下,目标函数随着服务水平提高而减少。过低的服务水平会导致目标函数成倍增长,这是因为当服务水平低于某一阈值,决策者不得不增加大量的物流基地使所有施工点被覆盖,而这个阈值是在40～60 km,因此在修建时,尽量不考虑 60 km以下的服务水平。

确定性模型不同服务水平下的选址结果见表6。山区道路交通基础差,因此在选择供应商时,决策者会更倾向于选择靠近铁路沿线的供应商q4和q6。在修缮铁路时,随着海拔的提高,因为物流基地要覆盖多个施工点,物流基地到施工点的运输难度会急剧提升,故决策者在选择物流基地时会考虑选择更靠近高海拔施工点的候选点。并且随着服务水平的提升,表中可以看出所选择海拔低的物流基地数量在降低,海拔高的物流基地数量几乎不变。对于永临结合的物流基地选择,在修缮完成后,决策者倾向于在低海拔和高海拔各选一个,实现对社会需求的服务。

表6 不同服务水平下的选址结果

3.3 鲁棒模型与随机模型结果对比

在不同服务水平下选取18组不同容忍水平的数值,以此探究容忍水平的敏感性。在均值与支撑信息已知的非精确集下,分布鲁棒优化(distributionally robust optimization,DRO)不同容忍水平最优值比较见图4。需要说明的是,通过3.2节的结果分析,服务水平为40 km的情况不予考虑。由此可以观察到,所有服务水平下,随着容忍水平的增加,最优值在降低,并且不断逐渐向确定性模型逼近。这表明过于保守的解会带来相对较高的成本,为了避免这种情况引入部分概率分布信息来降低成本是有必要的。决策者在实际问题中想避免风险拥有相对高的容忍度,可以选择获取更多的分布信息,由此使得模型越逼近确定性模型,成本将会越低。DRO模型不同服务水平下的各项结果见表7。与确定性模型不同的是,由于未来社会需求带来的不确定性,物流基地i8的优先级提高。原本被分配给物流基地i7的需求点,都被分配给了距离相近的i8。而决策者考虑到不确定性因素,选择了容纳更多未来需求的i8作为永临结合的物流基地而不是i3。

图4 DRO不同容忍水平最优值比较

表7 DRO不同服务水平下的选址结果

接下来将比较分布鲁棒优化模型与随机优化模型在本问题上的性能。随机优化模型不同于分布鲁棒优化模型,因为它需要不确定参数的精确概率分布,本文选择标准的高斯分布作为扰动参数精确的名义分布。相应的随机优化模型记为SO。根据以下定理得到具有高斯分布机会约束的等价的可计算确定性模型。

定理2若波动变量ξk之间相互独立且服从标准的高斯分布,则非精确机会约束式(12)的安全凸逼近的可计算确定性形式为

(26)

式中:Φ-1为标准正态分布的误差逆函数,是非精确机会约束(12)的安全凸逼近。

证明:由于波动变量ξk之间相互独立且服从标准的高斯分布。根据标准高斯分布,标准化约束(15)为

(27)

基于高斯分布的性质,可以得到

(28)

因此,当ε≤1/2 时有

(29)

将式(29)整理可得

(30)

结论得证。

SO模型不同容忍水平最优值比较见图5。与DRO模型类似,所有服务水平下,随着容忍水平的增加,最优值在降低。不同的是,不管是那种服务水平,SO模型整体最优值都是小于DRO模型的。因为SO模型中有精确的概率分布信息,从而降低了最优值,这和之前的结论是一致的。然而实际很难获得精确的分布信息,通过图6可以分析出DRO模型的必要性。图6展示了3种模型在容忍水平ε=0.209 6时,在不同服务水平下的最优值。确定性模型虽然最优值最小,但在不知道精确分布信息的情况下,往往会导致决策者做出错误的决策。SO模型总体明显高于确定性模型,表明有扰动的情况下确定性模型是失效的。在文献[12]中也明确指出了这一点:非常微小的扰动也可能会使确定性模型失效。而本文提出的DRO模型能够给出较为保守的决策,避免模型失效。

图5 SO模型不同容忍水平最优值比较

图6 不同模型最优值比较

为了更清晰地展示“多面体-DRO”模型的逼近效果,接下来将通过分布鲁棒代价(price of distributionally robust, PDR)来分析。假设ADRO是分布鲁棒优化模型的最优值,ASO是随机模型的最优值,则APDR的计算式为

(31)

不同服务水平下,不同容忍水平对应鲁棒代价见图7。由图7可以看到,最大的APDR不超过30%,并且在ε=0.209 6时最小的APDR近似为0。另一方面,容忍水平越高付出的代价越低,也就是说明过于保守的决策会让决策者承受相对较大的代价。有趣的是,PDR并不是随着服务水平单调的,服务水平低会增加物流基地选址数量从而增加不确定性,相反会增加单个物流基地的不确定性。因此选择合适的服务水平也是抵抗概率部分不确定性的有效手段。

图7 不同容忍水平下的鲁棒代价

4 结论

1)本文构建的评价指标体系,综合考虑山区铁路工程地质条件、永临结合建设模式、山区道路情况等因素,使问题更加贴合现实情况,能够更加完善地优化物流基地布局方案。

2)在以往研究基础上,本文在考虑当前的工程物流运输需求的同时,将社会需求分布纳入考量范围,并基于未来需求的不确定性,通过非精确机会约束,构建了适用于在山区永临工程设施选址的“多面体-DRO”二阶段分布式鲁棒模型,并推导出可处理形式,具有较强的适用性。

3)以山区铁路工程物流基地选址为例进行实例分析。结果发现决策者更倾向于选择靠近施工点的高海拔处的设施,而不是远离施工点海拔低且地质条件更好的设施;设施的服务水平是影响决策者设施选址的重要因素,合理的服务水平可以减少地质条件和经济因素对选址的影响;在具有不确定信息时,服务水平越高代价也越高,而本文的模型能有效避免这种情况,通过付出较小的代价来抵抗不确定性。为实际情况中山区物流基地选址布局规划、永临结合模式设施修建提供实证参考。