基于计算机视觉的钢桥螺栓松动检测方法

劳武略，徐 威，张清华，罗纯坤，崔 闯，陈 杰

(1.西南交通大学 土木工程学院，四川 成都 610031；2.保利长大工程有限公司，广东 广州 510620)

螺栓连接件结构简单、装卸便捷,已成为钢桥建设中的主要连接方式之一[1]。但在车辆、温度等动力荷载作用下螺栓极易发生松动,造成栓接结构预紧力不足、承载力下降。目前常用扭矩扳手进行螺栓松动检测,但该方法检测效率低、漏检率高,且因螺栓参数差异导致检测误差较大。因此,为保证钢桥栓接结构服役性能,需研发智能化、自动化的螺栓松动检测方法,提高检测效率和精度。

针对上述实际工程问题,国内外学者提出了以结构振动、压电阻抗、超声导波等为基本原理的螺栓松动检测方法[2]。在基于振动的技术中,主要通过结构的固有频率、模态和频响函数等动态特性分析螺栓状态[3]。在基于压电阻抗的技术中,利用压电材料将激励电压转换为振动信号,使得压电材料与螺栓结构形成的耦合系统发生谐振,根据谐振频率反演螺栓的预紧力[4]。在应用超声导波技术时,先利用压电材料激励出更高频的振动信号,从而在板件中产生超声导波,再根据导波的线性或非线性特征检测螺栓的状态变化[5]。然而这几类方法检测结果易受环境影响,且均需提取信号特征与螺栓状态间的复杂映射关系[6]。

近年来,基于计算机视觉的健康监测方法因其具有低成本、易部署、非接触测量等众多优点而受到学者们的广泛关注[7-9]。Pan等[10]利用终端设备采集松动前后螺栓头上预置的编码图像,在识别其编码特征后计算松动角度,但该方法检测成本较高,不适用于钢桥螺栓群的松动监测。随着深度学习理论的发展,国内外学者又提出以RCNN[11]、Yolo[12]、SSD[13]为代表的目标检测模型,其中Yolo已更新至YoloV5且具有较高的检测效率。陈永等[14]在Mask-RCNN的基础上提出一种铁路异物检测方法。Zhang等[15]和Yuan等[16]分别利用RCNN、Mask-RCNN检测外露螺杆的螺栓。程敦诚等[17]利用SSD定位并截取铁路接触网顶紧螺栓区域,并由此判断螺栓状态。为检测螺栓的松动角度,还需检测与螺栓相关的几何图素,并根据图素的相对位置关系计算角度。Yu等[18]和Zhao等[19]以SSD检测出的螺栓标记物为角度计算依据,但当标记物被遮挡或脱落时该方法将失效。文献[20-22]通过边缘检测、Hough变换等图像处理方法检测螺栓边线进而计算松动角度,但所采用的图像处理技术对外界干扰较为敏感且易发生误检,这导致其稳定性与精度均难以保证。为规避上述图像处理技术中的缺点,本文采用深度学习方法检测螺栓关键点,即六角螺栓的6个角点,并将其作为计算螺栓松动角度的几何图素。

基于深度学习的关键点检测是计算机视觉领域的另一个热点研究问题,其核心思想是利用神经网络提取图像特征,并由此确定关键点类别及位置[23]。多个目标的关键点检测可分为自上而下[24]和自下而上[25]2种方法。自上而下的方法中需先检测出图像中的目标,然后对每个目标的关键点进行检测。自下而上的方法则包含图像中所有关键点的检测与检出关键点的聚类组合。较于自下而上的方法,自上而下的方法检测精度较高,但检测速度稍逊。由于螺栓关键点检测精度将直接影响后续的角度计算,故本文采用自上而下的方法检测螺栓关键点。既有研究[24]表明,自上而下的方法中,在目标检测算法可检测出所有目标的前提下,其检测框的精度对后续关键点检测影响较小,如何提高关键点检测的精度才是至关重要的。为提高检测效率,本文先利用YoloV5检测图像中的螺栓目标,然后基于深度学习理论建立螺栓关键点检测模型,在比选出性能较优的关键点检测模型后,再利用该模型检测各个螺栓目标的关键点。

综上所述,本文提出一种基于计算机视觉的钢桥螺栓松动检测方法:首先建立螺栓关键点检测模型,分别构建YoloV5数据集和关键点检测模型数据集;然后训练检测模型,并在训练过程中比选出性能较优的关键点检测模型;利用训练后的YoloV5模型和关键点检测模型自上而下检测初始、松动状态图像中的螺栓目标及关键点,并根据关键点确定各个螺栓的中心点位置,再以中心点的相对位置矫正两幅图像的几何变形,并求解透视变换矩阵;最后利用透视变换矩阵对关键点进行重投影,根据松动前后关键点间的位置变化判断螺栓松动,并计算松动角度。

1 钢桥螺栓松动检测方法

1.1 基本原理

钢桥螺栓松动检测方法框架见图1。图1中,图像数据准备、模型训练是该方法的准备阶段,目的是生成2个数据集,分别训练Yolov5模型和关键点检测模型。该过程中螺栓目标和关键点均由人工标注,其中,目标标注结果中包含目标框的坐标和长宽信息,关键点标注结果中包含关键点的坐标信息。螺栓关键点检测步骤中,需利用训练后的2个模型检测初始、松动状态图像中的螺栓目标和关键点,检测结果包含检测框的坐标和长宽信息,以及关键点的坐标信息。其中螺栓目标裁剪时,需将目标框或真实框向外扩展20%后作为裁剪框,以保留充足的螺栓边缘信息。螺栓松动识别步骤中,需同时对初始状态图像和松动状态图像执行以下操作:

图1 螺栓松动检测方法框架

Step1将6个关键点坐标的平均值作为中心点的坐标,并采用基于Voronoi图确定边界点的方法分类匹配中心点。

Step2根据匹配结果拟合透视变换矩阵的最小二乘解,并利用该矩阵对螺栓关键点与中心点进行重投影。

Step3根据松动前后螺栓各点间的位置变化判断螺栓松动,并计算松动角度。

1.2 螺栓目标与关键点检测

钢桥螺栓通常分布较为密集,因此本文采用先检测螺栓再检测其关键点的方法。首先将图像输入至YoloV5得到螺栓目标的检测框,根据检测框裁剪原始图像得到螺栓子图块,然后利用关键点检测模型检测子图块中的关键点。螺栓目标、关键点检测过程见图2。图2中,w、h分别为检测框的长、宽;裁剪框为检测框向外扩展20%,即裁剪尺寸为1.2w×1.2h。

图2 螺栓目标、关键点检测过程

1.2.1 螺栓目标检测模型

螺栓目标检测模型见图3。图3中,Backbone(骨干网络)、Neck(特征融合提取结构)、Head(检测头)3个模块组成YoloV5[12];原始输入图像的像素尺寸为640×640×3(3个颜色通道);在Backbone模块,首先利用注意力机制对输入进行像素间隔采样生成4张图像,并对其进行卷积后生成初始特征图,再利用DarkNet53网络提取特征图中的纹理、形状等特征;在Neck模块,利用特征金字塔对不同尺度特征进行拼接融合,生成的特征图尺寸分别为128×80×80、256×40×40、512×20×20;在Head模块,将特征图映射为候选框的坐标、置信度、概率分布等7个参数,其中,置信度反映候选框内是否有目标的概率,概率分布是螺栓目标的分类概率。Head模块中的3组特征图分别用于预测大、中、小目标,各特征值的先验框数量为3,因此每个尺度下的参数预测数量为s×s×3×7,s为特征图的大小。

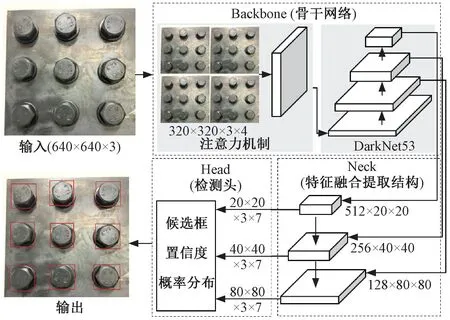
图3 螺栓目标检测模型

1.2.2 螺栓关键点检测模型

螺栓关键点检测模型见图4。当前常用的关键点检测思路有2种[26]:①利用Backbone提取图像特征,由全连接层直接回归关键点坐标,如图4(a)所示;②直接利用Backbone输出Heatmap(热图),通过Heatmap信息反算关键点的像素坐标,如图4(b)所示。前者在全连接层回归坐标时不会丢失数据精度,但缺乏泛化能力,即对未知数据的检测效果较差;后者需要高分辨率的Heatmap才能保证检测精度,但这使得模型计算量大,且反算关键点坐标过程是不可微的,导致无法对模型进行端到端的训练。综合考虑2种方法的特性,本文在Heatmap后接DSNT(可微变换)模块[26],将Heatmap回归为关键点坐标,使模型完全可微,如图4(c)所示。

图4 关键点检测模型

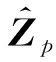
图5 DSNT模块结构

(1)

(2)

式中:winput、hinput分别为输入图像的宽度、高度。

X、Y矩阵的维度与Heatmap相同,X、Y矩阵中(i,j)处的元素Xi，j、Yi，j为

(3)

由此可知,DSNT模块不会引入额外的训练参数,且可通过低分辨率的Heatmap得到具有数据精度的关键点像素坐标。

在Heatmap回归过程中,由于螺栓关键点间的特征较为类似,为避免在某个通道的Heatmap中出现多个局部峰值,需将关键点分为6类。又由于螺栓关键点分布方位不同,考虑到关键点检测模型中的回归过程具有位置记忆,即可根据关键点的相对位置关系对其进行分类,故本文以左上关键点作为第一类关键点P1,然后沿逆时针依次为关键点P2～P6。左上关键点的判断准则为:螺栓中心点O与6个关键点构成向量集合OPi,i=1,2,…,6,单位向量[1 1]记为OP0,计算OPi与OP0之间的顺时针夹角值θi,θi最小的关键点作为螺栓的左上关键点。螺栓关键点分类见图6。

图6 螺栓关键点分类

关键点检测模型中的待训练参数仅来源于Backbone,其特征提取能力直接影响模型检测性能,而Heatmap大小将直接决定Backbone提取出的信息量。因此本文选取4种经典的图像分类网络:EfficientNet[27]、ResNet[28]、DenseNet[29]、MobileNet[30]分别作为模型的Backbone,对比不同Heatmap大小时的模型性能,以比选出更优的关键点检测模型。上述4种图像分类网络的输入图像像素尺寸为224×224,下采样率为25(5个步长均为2的下采样阶段),网络末端输出的特征图尺寸为dc×7×7,dc为通道数,经过池化层与全连接层后输出当前图像的分类结果。为将上述分类网络应用于关键点检测模型中,需进行以下改动:①将分类网络中某个下采样阶段的步长改为1,减小下采样率,使得网络末端输出的特征图尺寸变为dc×14×14;②将分类网络末端的池化层与全连接层改为卷积层,将dc×7×7(或dc×14×14)的特征图转换为6×7×7(或6×14×14)的Heatmap。

对上述关键点检测模型还需建立损失函数。本文将归一化的关键点坐标预测值与真实值的L2范数、Heatmap预测值与真实值的JS散度正则项共同作为损失函数,如图4(c)所示。L2范数可直接量化关键点预测位置与实际位置之间的距离,其计算式为

(4)

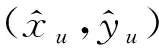
(5)

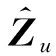
1.3 图像几何矫正

图像采集过程中,视平面与螺栓所在平面(物面)难以保证平行关系,导致图像存在几何变形,此时视平面中的物像无法正确反映出物体的角度特征。因此需矫正图像的几何变形,使图像中的角度关系具有实际的物理意义。首先将1.2节中检测出的6个关键点的坐标平均值作为中心点的坐标,并匹配中心点,即将各中心点坐标作为矫正前的坐标,在确定各中心点的相对位置后,指定各中心点几何矫正后的坐标。随后根据矫正前后的中心点坐标求解透视变换矩阵,并对关键点进行重投影,图像几何矫正过程见图7。图7中,物面、视平面、视点构成了基本的透视投影模型,其实质是以中心点的相对位置关系为参照,重新建立投影体系,将视平面中的物像投影至与物面平行的重投影面上。

图7 图像几何矫正

1.3.1 螺栓中心点匹配

螺栓中心点匹配过程见图8。由于图像中的螺栓数量未知,且在几何矫正前螺栓中心点呈不规则离散分布,如图8(a)所示,这对中心点匹配方法的准确性和稳定性提出了较高要求。为实现中心点的自动化匹配,本文采用基于Voronoi图确定边界的方法对螺栓中心点由外至内逐层分类,再根据过各点特定斜率直线的坐标轴截距确定每层边界点的拐点,并以这些点为参考将各点与实际的螺栓逐个对应,最终确定矫正后各点的像素坐标。

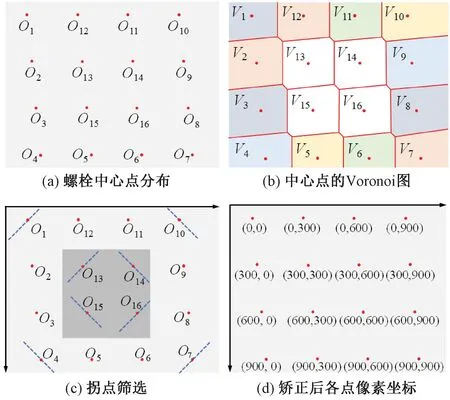
图8 螺栓中心点匹配

对于本文中的螺栓中心点,其Voronoi图的定义为[31]:设{O1,O2,…,On}为螺栓中心点集合,对于该集合中任意点Oi,平面中与Oi最为接近的点集构成一个多边形区域Vi,称为Oi的Voronoi区域,如图8(b)所示。由此可以看出,Voronoi图将无限平面划分为有限个区域,记为{V1,V2,…,Vn},当Vi无界时,可判断与其相关联的Oi为边界点。图8(b)中的V1～V12均是无界的,因此可将O1～O12分类为第1层边界点。剔除中心点集合中的第1层边界点后,对剩余点重复上述分类过程,并依次记为第2层边界点、第3层边界点,等等,直至对所有点均进行了分类。

完成螺栓中心点分类后,先求解图像坐标系中,过各点且斜率分别为±1的直线与坐标轴的截距,并根据截距大小关系筛选出各层边界点的拐点,如图8(c)中所示。对于第1层边界点,过所有点且斜率为-1的直线与竖轴的截距最小值、最大值分别对应的点为O1、O7,过所有点且斜率为1的直线与横轴的截距最小值、最大值分别对应的点为O4、O10;第2层边界点、第3层边界点等同理。确定每层边界点的4个拐点后再分别指定各中心点矫正后的像素坐标,如图8(d)所示。

1.3.2 透视变换原理

从数学角度而言,透视变换就是坐标系的转换,包含线性变化、平移变化、透视变化。其中,线性变化与平移变化不会改变图像中的平行关系,透视变化会在三维空间中改变重投影面方位。本文为计算图像中的角度特征,取重投影面与物面平行,即属于二维平面的透视变换,该变换过程[32]可表示为

(6)

式中:M为透视变换矩阵;(xo,yo)为中心点矫正后的像素坐标;(x′o,y′o)为中心点矫正前的像素坐标;f为尺度因子。M矩阵中有8个未知参数,每个中心点变换前后像素坐标可提供2个独立方程,因此求解M矩阵至少需要4个中心点的变换前后像素坐标。

1.4 螺栓松动检测

利用求解出的透视变换矩阵对螺栓关键点进行重投影,可使各点的相对位置反映出真实的角度关系,并进一步根据松动前后关键点间的位置变化计算松动角度。但关键点检测时存在离散误差,且该误差会在透视变换矩阵求解与重投影过程中放大,这将会影响向量夹角的计算精度。因此,需统计分析螺栓向量夹角的误差分布,并确定判断螺栓松动的阈值。

图9 角度计算

2 试验与数据分析

2.1 图像数据准备

利用消费级相机采集某钢桥栓接结构的高强螺栓图像,并通过变换图像采集的角度、距离、光照等获得大量不同质的螺栓图像,以保证数据集的复杂性与多样性,最终共采集螺栓图像1 340张。

图像采集完成后,需对图像进行标注,标注过程见图10。首先标注每张图像中的螺栓目标真实框,如图10(a)所示,然后将真实框向外扩展20%后作为裁剪框,裁剪完成后得到1.4万张螺栓子图块。为便于将子图块输入到关键点检测模型中,本文将所有子图块的像素尺寸统一为224×224。其次按图6所示的关键点分类顺序标注每个子图块中的6类关键点,标注过程见图10(b)。所有关键点的分布见图11。由图11可知,每类关键点分布集中且相对位置关系明确,关键点检测模型可学习到这种关键点的分布特征,并在预测过程中根据位置关系判断点的类别。

图10 图像标注

图11 关键点分布

2.2 模型训练过程

2.2.1 目标检测模型

采用迁移学习方式对YoloV5进行训练,即预加载已在其他大型数据集中训练后的模型参数,使其快速收敛。为真实反映模型检测性能,需统计分析YoloV5识别结果的精确率p和召回率r,其计算式分别为

(7)

式中:TP为真阳性识别结果;FP为假阳性识别结果;FN为假阴性识别结果。同时引入交并比IoU,反映预测框与真实框的相关度。对于所有预测框,其IoU为

(8)

取交并比阈值为0.6,当预测框的IoU值大于0.6时预测结果为TP,当预测框的IoU值在0～0.6范围内时预测结果为FP,当预测框与真实框没有交集即IoU值为0时预测结果为FN。因此p衡量了模型检测的查准度,r衡量了模型的查全度。

YoloV5训练过程中p、r变化趋势见图12。由图12可知,训练前期网络泛化能力较差,网络性能波动较大;经40次迭代训练后,p、r趋于平稳,训练结束后p、r分别达到了0.99、0.98,表明网络已达到较好的检测性能。

图12 YoloV5性能曲线

2.2.2 关键点检测模型

影响关键点检测模型性能的主要因素有2个:①Backbone特性与数据集特征的匹配程度;②Heatmap的大小。因此针对4种Backbone,分别取7×7与14×14两种Heatmap大小,组合成多种不同的网络结构,其中ResNet、DenseNet、EfficientNet、MobileNet的参数量分别为23.5、7.0、4.2、3.1 MB,训练过程中各网络的损失函数见图13。由图13可知:训练过程中,ResNet由于待训练参数量较大,其损失收敛较慢,而MobileNet则收敛较快;训练结束后,当输出Heatmap维度为14×14时,其模型损失低于Heatmap维度为7×7时的模型,原因是此时Heatmap所描述的分布概率更加精细,其预测结果也更加精准,不同Heatmap大小时关键点的分布概率见图14。由于ResNet参数量较大,其特征提取能力更强,因此本文将以ResNet作为螺栓关键点检测模型的Backbone,Heatmap大小取14×14。最终,利用YoloV5与关键点检测模型对图像中的所有螺栓关键点进行检测,检测结果见图15。

图13 关键点检测模型损失函数

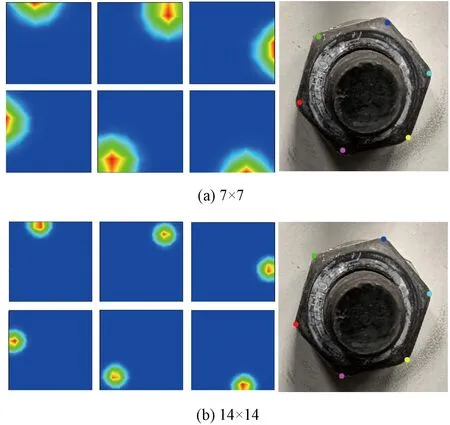
图14 不同Heatmap大小时关键点的分布概率

图15 螺栓关键点检测结果

2.3 透视变换矩阵求解

在得到螺栓关键点的像素坐标后,将其坐标的均值作为螺栓中心点的坐标,采用1.3节中所述方法对中心点由外至内逐层分类并确定各点矫正后的像素坐标,图像矫正过程见图16。为求解透视变换矩阵,式( 6 )可改写为

图16 图像矫正过程

(9)

式中:n为螺栓中心点数量。当n=4时,该方程组有唯一解,即透视变换矩阵唯一确定;当n>4时,该方程组为超定方程组,其最小二乘解即为最优的透视变换矩阵。利用该矩阵对螺栓图像进行透视变换,结果见图16(b)。

图17 分布

2.4 方法有效性验证

为验证本文所提出的钢桥螺栓松动检测方法的有效性,分别对不同采集环境下的螺栓松动进行识别,螺栓松动识别过程见图18～图22。验证步骤如下:

图18 螺栓松动图像采集

Step1选取某背景较为复杂的钢桥拼接板结构采集初始状态图像,如图18所示。

Step2将4、6号螺栓分别松动20°、25°,并分别控制图像采集距离d=0.9～1.8 m(θ=0°)、角度θ=10°～40°(d=0.9 m),得到多个松动状态图像。其中,d为图像采集设备视点至螺栓平面的距离;θ为图像采集设备视线与螺栓平面法向的夹角。

Step3利用本文方法分别对初始状态图像和松动状态图像,进行螺栓目标及关键点检测、图像几何矫正、关键点定位误差分析、角度计算,如图19～图21所示,最终得到螺栓松动检测结果,见表1。

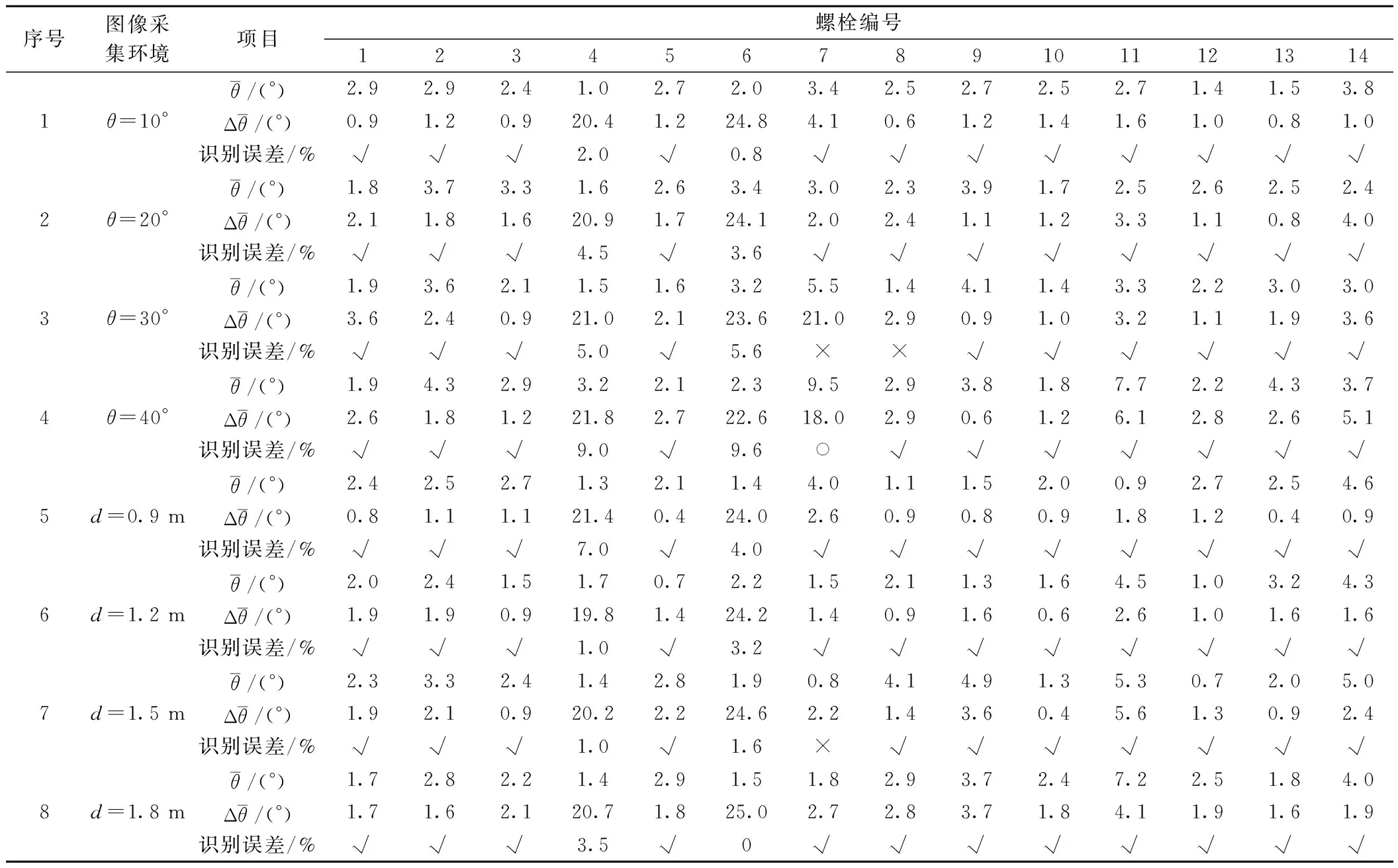
表1 螺栓松动检测结果

图19 螺栓目标及关键点检测

图20 螺栓松动图像几何矫正

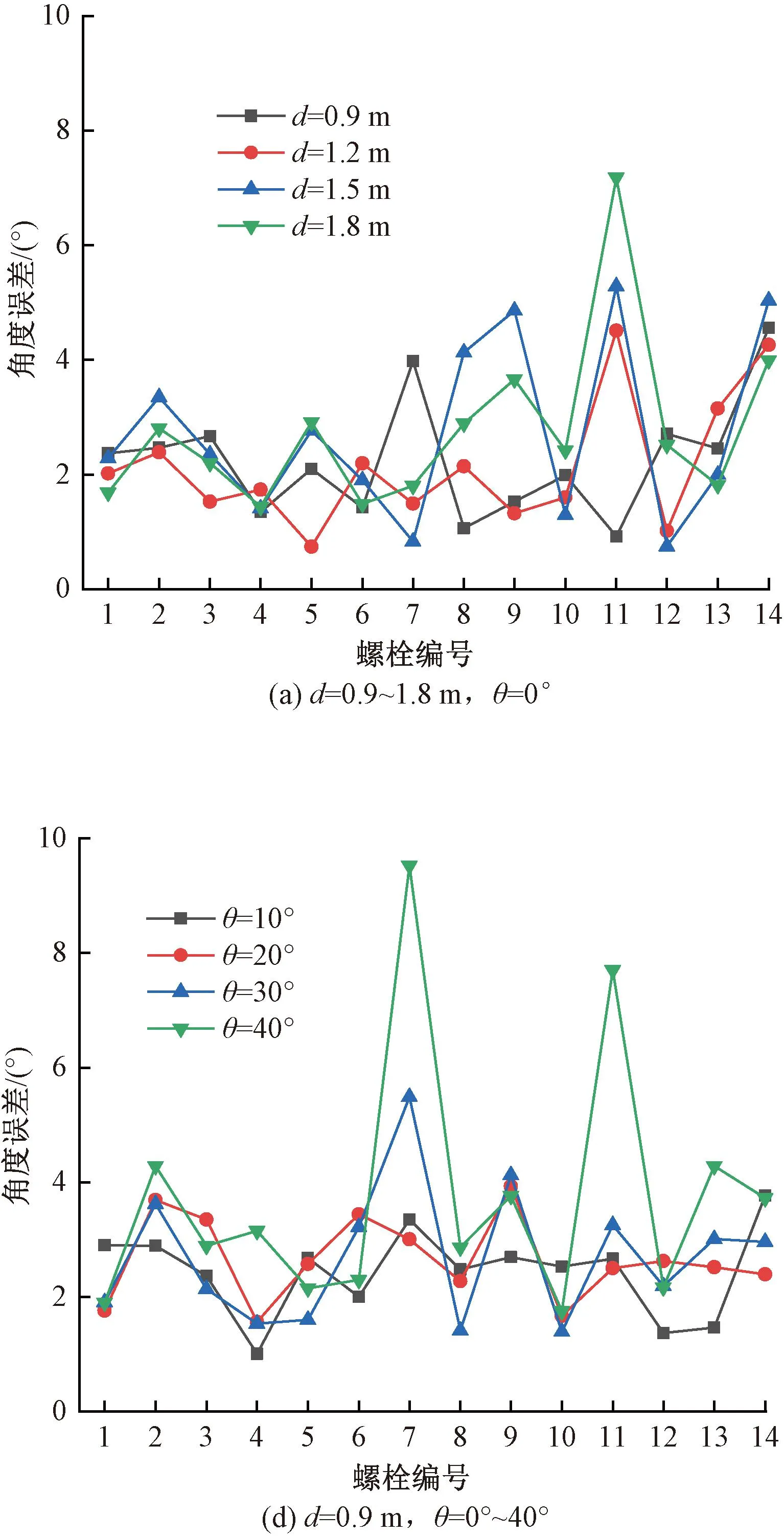
图21 螺栓松动识别过程中分布

上述步骤在配置CPU和GPU的实验平台上进行,其中运算量较大的步骤是螺栓目标检测和关键点检测,分别为16.3 GFLOPS和32.3 GFLOPS,最终检测每张图像耗时约0.33 s,即可达到3帧/s的检测速度。

由图18～图22、表1可知:

图22 螺栓松动识别过程中分布

1)本文采用的目标、关键点检测方法在不同图像采集环境下均能检测出螺栓目标及关键点。

5)利用本文方法识别螺栓松动时,4、6号螺栓的松动角度计算误差在不同图像采集环境下的最小值分别为1.0%、0%,最大值分别为9.0%、9.6%,均在可接受范围内,最终在所有图像采集环境下仅发生3例误检,误检率为2.7%,表明本文所提出方法具有较高的检测精度与稳定性。

3 结论

对于不同图像采集条件下的钢桥螺栓,本文提出基于计算机视觉的螺栓松动识别方法,可实现螺栓目标及关键点检测、图像几何矫正、角度计算等,并通过对比初始状态图像与松动状态图像中关键点的位置变化识别螺栓松动,大幅提升螺栓松动检测的自动化程度。结果表明:

1)由于钢桥螺栓分布较为密集,本文采用自上而下的方法检测螺栓关键点,先利用YoloV5检测螺栓目标,然后基于深度学习理论建立多个关键点检测模型,通过比选各个网络的性能最终确定以ResNet作为Backbone,并取特征图尺寸为14×14;利用该目标检测模型与关键点检测模型可较为准确地检测出螺栓的6个关键点。

2)由螺栓关键点确定中心点位置,基于Voronoi图分类、匹配中心点进而矫正图像的几何变形的方法具有较好的稳定性,且由所有中心点像素坐标拟合透视变换矩阵最小二乘解,可提高图像几何矫正的精度。

3)利用本文方法检测不同图像采集环境下的关键点时,检测误差总体上表现出随图像采集距离、角度的增大而增大,且对图像采集角度更为敏感,因此还需提高关键点检测的鲁棒性,提高本文方法在恶劣图像采集环境下的适用性。

4)不同图像采集环境下,松动螺栓的角度检测误差在0%～9.6%之间,误检率仅为2.7%,表明本文所提出方法的检测精度和稳定性均较高。