DFSL：基于细粒度共享层激励机制的深度联邦学习算法

张浩宇，巫朝霞（通信作者）

（新疆财经大学统计与数据科学学院 新疆 乌鲁木齐 830012）

0 引言

联邦学习的本质是一种分布式机器学习技术，旨在保护用户数据隐私的前提下通过协同训练模型，使得每个参与方的局部模型能够从其他参与方的模型中受益，从而不断提升整体模型的性能。［1］至今联邦学习已经应用到了各个领域，如工业物联网领域［2］、医疗领域［3］、无线通信领域［4］、金融领域［5］等。 对于联邦学习的研究，众多学者都致力于开发联邦学习算法，以支持机器学习模型的有效性。 例如2020 年Liu 等［6］采用了深度神经网络，引入联邦迁移学习（federal transfer learning，FTL）来改进数据联合下的统计建模。 FTL 允许在不侵犯用户隐私的情况下共享知识，并实现跨领域传输补充知识，使目标领域能够利用源领域的丰富标签构建灵活有效的模型。 该框架对现有模型结构进行了最低程度的修改，并提供了与非隐私保护迁移学习相同的准确性。 不同于前面的学者，为了在不侵犯用户隐私的前提下，实现多方之间协作构建机器学习模型的目标，Cheng 等［7］于2021 年提出了一种名为SecureBoost 的新型无损隐私保护树增强系统，采用梯度提升决策树的方法进行设计。 该系统具备多方共同进行训练的能力，并且能够在不泄露用户数据隐私的条件下，达到与非隐私保护方法相当的准确率。 然而上述大多研究都没有考虑到联邦学习涉及具有异构环境的参与者。

为此，2020 年Lu 等［8］提出了一种名为隐私保护异步联邦学习机制（privacy⁃preserving asynchronous federated learning mechanism，PAFLM ）的隐私保护异步联邦学习机制，该机制使得多个边缘节点能够在不共享其私有数据的情况下进行联邦学习。 首先，该机制能够在训练过程中有效压缩节点和参数服务器之间的通信，同时保持模型的准确性。 其次，该机制还允许节点在学习过程中的加入或退出，从而更好地适应边缘移动设备的异构环境。 2022 年Nguyen 等［9］明确指出同步联邦学习在并行训练的数百个客户端上无法有效扩展，会导致模型性能和训练速度的回报递减问题。 为应对此问题，他们提出了一种名为FedBuff 的全新缓冲异步聚合方法，该方法综合了同步和异步联邦学习的最佳特性。 研究证明，FedBuff 方法不仅比同步和异步联邦学习更高效，还能与诸如安全聚合和差分隐私等隐私保护技术相兼容。 2023 年，Zhang 等［10］对异步联邦学习方法可能导致训练精度下降和收敛速度变慢的问题进行了研究。 他们提出了一种名为TimelyFL 的异构感知异步联邦学习框架，该框架具有自适应训练功能，会根据每个客户端的实时资源能力来调整本地训练工作量，以确保更多可用的客户端能够参与全局更新而不会过时。 与Nguyen 等［9］提出的FedBuff 方法相比，TimelyFL 在参与率、收敛率和测试准确性方面都有所提高。

此外，在联邦学习中，如果没有合适的激励机制，很多数据所有者会不愿意贡献自己本地模型的参数，积极地参与全局模型的训练。 特别是当数据所有者是企业的情况时，因为这些数据往往可以给企业带来一定的经济收益，因此如何评估不同数据所有者的贡献对设计激励机制至关重要。 Yang 等［11］在2023 年认为激励机制上公平性与帕累托（Pareto）效率之间存在冲突。 为了解决该问题，他们提出了一种将shapely 值与帕累托效率优化相结合的激励机制。 该机制引入了第三方监督收益分配，并根据是否达到帕累托最优选择对参与方进行奖惩。 在达到帕累托最优的情况下，根据Shapely 值法进行奖励分配；反之，则进行处罚。 不同于前面的学者以数据质量为导向计算贡献从而设计激励机制方案，Zhan 等［12］采用训练数据的数量作为计算客户贡献度的指标，并利用Stackelberg 博弈的概念描述了参数服务器和客户之间的交互。 在完全信息共享的场景下，他们推导出了纳什均衡解，并针对缺乏先验信息的场景，设计了一种基于深度强化学习（deep reinforcement learning，DRL）的联邦学习激励机制。

以上研究从本地数据异构、梯度保护、优质客户端选择、通信成本和算力资源等角度分别研究了基于深度联邦学习框架下的隐私保护问题，且已取得了较大的成果。 对于一个基于深度学习的联邦框架而言，其核心模块是深度学习网络，共享参数往往是分布在不同的层，共享参数梯度的计算以及全局模型对共享参数的广播也是基于共享层的。 故细粒度共享层的适当激励，能够快速地判断共享参数对全局模型收敛的贡献大小，从而指导算法设计人员优化深度学习模型。 基于此，本文提出基于细粒度共享层激励机制的深度联邦学习算法（deep federated learning algorithm based on fine⁃grained shared layer incentive mechanism，DFSL），该算法的主要贡献如下：

（1）采用N 组本地变量实现对不同共享层的加权，实现自适应的共享层参数更新，同时本地梯度上传时，基于这N 组共享实现对梯度的隐私保护；

（2）本文提出了基于余弦相似度的客户端选择方法，将各客户端上传的梯度进行余弦相似度计算得到距离，然后使用裁剪的方法随机去除部分相似度过小的梯度，实现优质客户端梯度的选择；

（3）本文提出的算法在CIFAR－10 以及MNIST 两个数据集上的召回率以及F1 值均达到了最优。 在CIFAR－10 数据集上召回率以及F1 值分别提升了3.73%以及2.12%；在 MNIST 数据集上分别提升了 1.99% 以及2.10%。

1 相关理论

1.1 联邦学习基本框架

联邦学习框架基本组成部件如下：

（1）本地模型。 本地模型也称客户端模型，主要由计算资源、联邦框架下的机器学习模型、通信接口组成；本地模型以分布式的方式围绕全局服务器部署，且拥有私有数据集，各本地模型的私有数据集不进行共享。

（2）全局模型。 全局模型作为中心服务器，主要功能是安全聚合分布式客户端上传的梯度，然后将共享参数广播至各客户端。

（3）隐私保护。 联邦框架下，隐私保护主要有两个层面：数据层面、参数层面。 数据层面即使用加密算法实现对数据的硬加密，保证数据的本地存储安全；参数层面即使用加密或差分的方法将共享参数进行等同变换，既保护了原始数据的隐私安全，也不妨碍联邦学习过程中对真实数据分布的学习。

（4）安全聚合。 联邦基本框架下梯度聚合方式有两种：同步梯度聚合、异步梯度聚合。 前者要求所有客户端均上传完梯度后才进行聚合；后者不需要等待所有的客户端上传梯度，在合适的时机就开展梯度聚合，能够有效地避免因客户端掉线而产生的漫长等待问题。

（5）共享参数下发。 全局服务器在迭代更新自身参数的过程中，会将自身参数通过广播或者选择的方式分发给本地模型，本地模型使用这些参数更新自身参数，直至收敛。

联邦学习的基本框架如图1 所示。

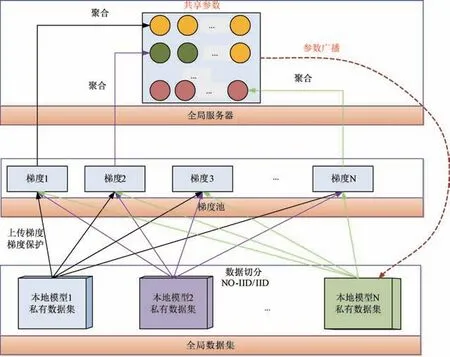
图1 联邦学习方法基本框架

由图1 可知：各本地模型数据集可以是独立同分布（independent and identically distributed，IID），也可以是非独立同分布（non⁃independent and identically distributed，Non⁃IID），数据集一旦分配完成之后，各本地模型之间就不再共享私有数据集。 各本地模型将本地的参数梯度计算出来之后传递至梯度池，由梯度池进行临时存储。

图1 中，梯度池N 表示共享参数个数，每一个共享参数均有独立的内存，当达到聚合条件时开始聚合，聚合方式如式（1）所示。 式（1）中，k表示第k个共享参数，B表示批次大小，表示第k个共享参数聚合后的梯度，δ是形式化的梯度保护函数，x是私有参数。 对客户端来说，私有参数是不共享的参数，θ是共享参数集合，梯度基于共享参数计算得到，j表示联邦学习迭代的第j个轮次。

由于客户端数据划分存在两种方式，故对应这两种方式下，数据划分公式分别如式（2）和式（3）所示。 其中，参数S表示本地客户端的个数，Di表示第i个客户端的私有数据集， ‖Di‖ 表示数据集Di的规模，D表示全局数据集。

式（2）是放回式抽样，产生S个私有数据集，且存在i，j，使得Di∩Dj≠Φ。 式（3）是不放回抽样，即所有的本地客户端样本均不相交，并集为全集D。

1.2 隐私保护

隐私保护是联邦学习的主要特性之一。 联邦学习过程中存在频繁的参数共享和传递，存在参数泄露和恶意客户端的虚假梯度共享。 因此数据隐私保护对于联邦学习至关重要。

数据隐私保护主要体现在两个方面：对样本数据进行隐私保护；对客户端和服务器端的内部数据变换结果进行隐私保护。 实现数据隐私保护的具体实施方法有以下两种：基于同态加密、 数据加密标准（data encryption standard，DES） 等密码学加密手段、 基于差分隐私（differential privacy，DP）的隐私保护。

（1）基于密码学的数据隐私保护。 数据集加密对硬盘要求高，且需要更高的通信带宽，加密算法如式（4）所示。

由式（4）可知，原始样本用矩阵W表示，维度大小为M×N，j，k分别表示当前矩阵的行号和列号，数值wj，k被加密成长度为R的向量，其数据规模是原来的RM＋N倍。可见，通信链路传输此种矩阵时，需要消耗大量的通信带宽和算力资源。

（2）基于DP 的隐私保护。 基于DP 的隐私保护的核心算法主要包括：基于高斯噪声的差分、基于拉普拉斯函数的差分。 前者适用于指数的数据隐私保护，后者适用于一般数据的隐私保护。 基于拉普拉斯函数的差分方法的隐私保护算法基本形式如式（5）所示。

式（5）中可看出，基于拉普拉斯函数以及当前梯度生成差分项结合当前梯度形成新的梯度值，得到新的梯度。成为候选梯度，被全局模型进行聚合，更新共享参数。 参数γ的作用是标定差分前后梯度的敏感度。且满足如下关系：（1）当γ＝0 时，差分项为0，原始梯度未进行任何隐私保护；（2） 0＜γ→0 时差分项随着γ增大而逐渐增大，与▽j，k的差异在一个合理的范围内时，隐私保护恰到好处；如果与▽j，k的差异很小，那么隐私保护力度仍有待加强；（3）γ→1 时差分项随着γ增大而逐渐增大，与▽j，k的差异越来越大且明显。 拉普拉斯函数基本公式如下：

2 基于细粒度共享层激励机制

本文提出了一种基于细粒度共享层激励机制的隐私保护算法：DFSL。 接下来本文将分别介绍算法DFSL的基本框架、原理以及对比实验。 为方便对算法描述的需要，现将后续将要使用到的参数汇总如表1 所示。

表1 参数列表

2.1 DFSL 算法基本架构

DFSL 算法的基本架构如图2 所示。 图2 主要由3 个模块组成。 分别是：多组本地模型、全局客户端、梯度队列容器。 为简单起见，每个本地模型均只包含私有数据集以及内置同构深度学习模型。 同构深度学习模型见图2 的“DFSL 模型”模块。

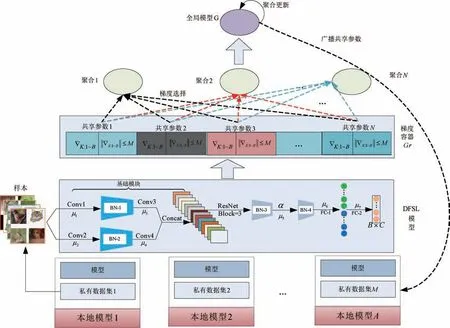
图2 DFSL 算法基本架构

DFSL 算法的联邦执行过程如下：

Round－1：本地模型首先使用私有数据集训练自身内置神经网络Netk，其次计算共享参数的梯度，使用μk作为梯度激励因子给原始梯度增加差分噪声，最后将变换后的梯度上传至梯度容器。 在此过程中，梯度激励过程如式（7）所示。

从式（7）中可看出，本文算法将每一层的激励矩阵与基于拉普拉斯差分项的乘积作为对应梯度的差分项。 由于激励矩阵μj使用sigmoid 函数激活，故能够保证差分项的非线性。

由于μj的初始值为全1 矩阵，DFSL 算法收敛过程中，μj矩阵逐渐向着最优值收敛，且均值在0 ～1 之间，故，，▽j，k） 。

Round－2：异步梯度聚合。 考虑到客户端的算力和信道，采用异步的方式实现梯度聚合。 设置阈值，当梯度容器Gr收集的梯度数目达到λ时，全局模型一次性清空Gr，计算共享参数的平均梯度，然后进行聚合。 具体过程如算法1 所示。

算法1：梯度聚合

输出：Gr*

客户端计算共享参数梯度**／

Round－3：共享参数传播。 全局服务器更新完自身参数后，将共享参数分享至参与训练的本地模型，各本地模型通过共享参数更新本地网络。

从图2 中可看出，本地模型与全局模型之间是通过共享参数进行耦合，共享参数越多，耦合得越紧密。 DFSL 算法基本框架满足以下几点：

（1）不同本地模型之间不建立通信，禁止共享私有数据。

（2）全局模型在广播共享参数时，只广播至与其建立梯度链接的本地模型，未建立通信链接的本地模型物理上无法收到全局模型的共享参数。

（3）共享参数被异步更新，已经被使用过的共享参数梯度将不再被使用。

2.2 DFSL 算法的同构网络

图2 中的DFSL 模型即为DFSL 算法的同构网络。 该网络主要由3 部分组成：

（1）基础卷积。 基础卷积的作用是使用若干个卷积模块实现对原始样本的变换和降维。 基础卷积的基本构造为两个平行的卷积网络，经过两层卷积之后进行了特征图的融合。

（2）残差模块。 残差模块主要由3 个残差Block 组成，残差模块具体形式如图3 所示。

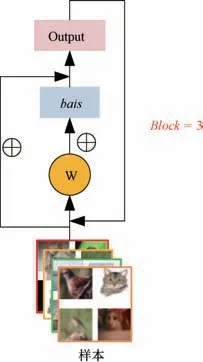
图3 残差模块

（3）全连接（fully connected，FC）层。 本文算法主要有两个级联的全连接层，由于全连接层输入时残差网络的输出，为了避免全连接层矩阵太过庞大，故设置两个全连接层，减少全连接层矩阵规模。 为更进一步描述图2 的同构网络结构，现将图2 的网络结构描述如表2所示。

表2 DFSL 算法同构深度学习模型参数

假设输入样本规模为B× 28 × 28 ×3，网络基本结构如表2 所示：

3 对比实验

3.1 实验环境

本文所使用的数据集为CIFAR⁃10、MNIST 图像数据集，这2 个数据集将会在后文介绍。 本文提出的算法可在GPU 快速部署运行，与其他算法在GPU 上进行对比实验，对比实验硬件配置如表3 所示。 实验超参数设置如表4所示。

表3 实验硬件条件

表4 实验条件设置

3.2 数据集

本文算法与对比算法在多个数据集上进行对比实验，本文所使用的数据集的基本信息如表5 所示。

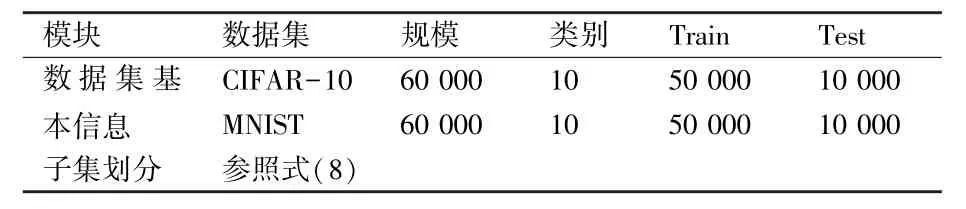
表5 实验数据集的基本信息

表6 对比算法以及评估指标

式（8）中，Um，d指第m 个客户端的数据集，‖D‖ 是全局数据集D 的规模。

因为本文的深度学习算法引入了差分隐私机制所以选用作为对比的算法也需要引入该机制，由表7 可知，本文所选用的对比算法有三种分别是ResNet⁃Block3 ＋DP、BiLSTM⁃CNN＋DP、CNN ＋DP。 其中ResNet⁃Block3 ＋DP 是结合了ResNet 的残差网络结构以及差分隐私机制的一种深度学习算法；BiLSTM⁃CNN＋DP 是一种结合了双向长短期记忆网络（bidirectional LSTM）和卷积神经网络（CNN）并应用了差分隐私DP 技术的算法；CNN＋DP 是一种使用了卷积神经网络和差分隐私技术的算法。

表7 2 个数据集上的准确率实验结果汇总 %

使用的4 种准确率计算过程如式（9）所示。

其中，TP 是真阳例，FP 是假阳例，FN 是假阴例，TN是真阴例。

3.3 实验

实验的评估指标分别是Accuracy、F1、Precision、Recall。 测试过程中收敛时步数以及在4 个评估指标上的实验结果汇总如表7 所示。

从本文算法在2 个数据集上的实验结果可看出，本文实验具有较好的鲁棒性，4 种评估指标下的实验结果均较高。 为验证本文提出的DFSL 算法对图片数据集的有效性，本文算法与目前已有的算法实验结果对比如表8 所示。 从表8 可看出，本文所提算法DFSL 在CIFAR⁃10、MNIST 等2 个数据集上的实验结果优于其他算法在原始数据集上的实验结果。

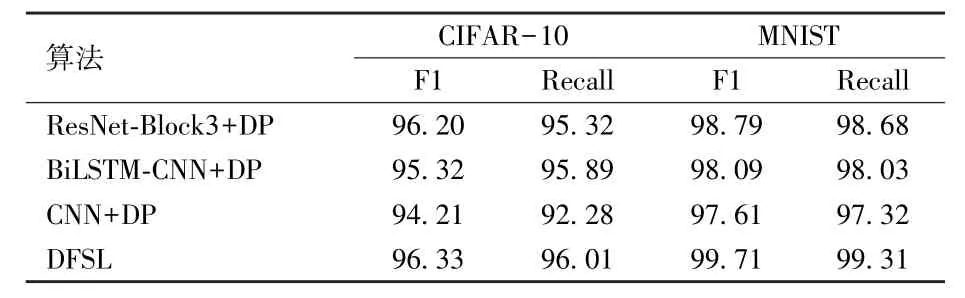
表8 与其他算法的准确率对比实验结果 %

为进一步量化DFSL 算法相较于其他对比算法在以上两个数据集上的分类准确率提升情况，在2 个数据集上评估指标提升汇总如表9 所示。

表9 与其他算法的对比提升率结果 %

从表8 和表9 可看出，以F1 为评估指标条件下，在CIFAR－10 数据集上F1 值最大提升2.12%、最小提升0.13%；在Mnist 数据集F1 值最大提升2.10%、最小提升0.92%；本文算法实验准确率完全超过CNN ＋DP 以及BiLSTM⁃CNN＋DP 算法。

基于以上对比结果，本文算法在对比指标上的单个对比算法上的提升率均为正，实验表明本文算法具有一定的优势。

由于本文算法使用了基于自适应差分方法对梯度进行了激励，为进一步比较本文算法与其他算法在收敛时间上的优势，将收敛时间汇总，如表10 所示。

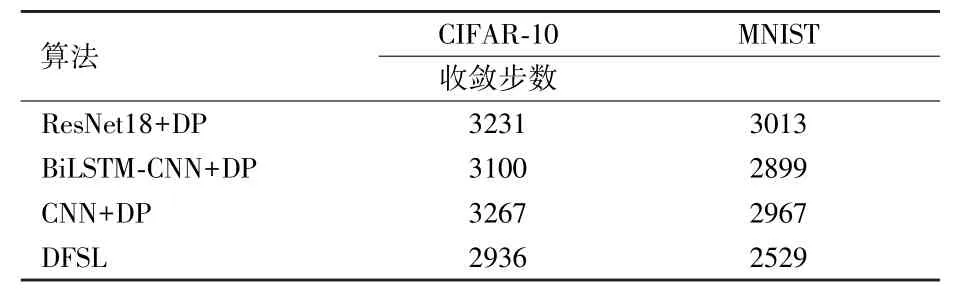
表10 与其他算法的收敛时间对比结果

从表10 可看出，本文算法虽然使用了较多的卷积模块，但是自适应参数随着训练的持续进行，得到了快速的收敛，使得最终算法在收敛时间上达到了最少的步数，相对于对比算法，本文算法在收敛步数上有较大优势。

4 结论

本文提出了DFSL算法分别对CIFAR⁃10、MNIST 进行了预处理，使用激励函数实现对梯度的快速隐私处理。 基于此，本文算法与对比算法在数据集上的实验表明，DSFL算法具有更高的准确率，且优于其他算法。 从评估指标对比结果来看，在CIFAR⁃10、MNIST 两个图像数据集上有更高的准确率。 后续将尝试使用聚类的方式对优质梯度进行定向选择，提高对样本特征提取性能，在更多的数据集上进行验证实验。