基于计算机仿真的功能梯度陶瓷材料刚柔耦合动力学问题研究

蔡丽江

（广州华商学院 广东 广州 510030）

0 引言

转子叶片用陶瓷材料可作为旋转中心刚体—柔性梁结构进行动力学研究，在热环境下高速旋转的叶片所承受的热应力以及旋转刚体运动与柔性梁变形耦合作用对叶片的工作强度会产生很大的影响［1－3］。 本文针对具有内冷通道且截面尺寸不一致的旋转中心刚体—梯度功能材料柔性梁在热环境下的动力学特性进行了研究，先后分析了物理弯曲引起的非线性耦合变形量和外高温、内冷却条件下柔性梁的温度场分布，并通过计算机仿真说明了叶片陶瓷材料的实际动力学特征。

1 功能梯度陶瓷材料模型建立

具有内冷通道的旋转中心刚体—FGM 柔性梁模型如图1 所示。 中空的柔性梁安装在圆形横截面的中心刚体上，中心刚体半径为R，围绕Z 轴高速旋转，O－XYZ是模型运动的惯性坐标系。τ为驱动系统旋转的外部作用力的力矩，l为柔性梁长度，he（x）为梁的横截面高度，be（x）梁的横截面宽度，内冷通道即中控部分的高度和宽度分别为hi（x）和bi（x）。

图1 旋转中心刚体－FGM 柔性梁模型

柔性梁的外表面两侧采用的是耐高温陶瓷材料，且由外到内材料按照幂律渐变为金属，具体的材料梯度分布形式如式（1）所示。

具体的参数取值分别为am＝2.3×10－5，Km＝204，ρm＝2.707×103kg／m3，Em＝7.0×1011Pa，ac＝1.0×10－5，Kc＝209，ρc＝3.0×103kg／m3，Ec＝1.51×1011。

1.1 热传导方程

本文的研究基于转子叶片在相对稳定高温条件下的动力学特性，因此将外部温度T1和内冷温度T0设定为恒定值，由此柔性梁的热传导方程可表示为式（2）所示。

假定横向对称面两侧实心处的温度为T0，那么实心部分的边界条件即如式（3）所示。

式（2）与式（3）相结合可得到实心部分的温度分布函数如式（4）所示。

1.2 动力学方程

针对柔性梁的物理变形所建立的浮动坐标系o′xyz如图2 所示。 该坐标系中o′x轴与惯性坐标系OX轴的夹角为θ，由于FGM 梁沿厚度方向材料的幂律渐变，所以柔性梁的热传导系数k（y）、热膨胀系数a（y）、材料密度ρc（y）、弹性模量E（y）均为以y为自变量的函数。

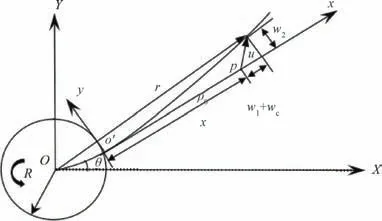
图2 FGM 梁浮动坐标系

在图2 中，柔性梁发生变形后其任意一点p在浮动坐标系中的矢量半径表达式如式（5）所示。

2 计算机仿真分析

2.1 已知大范围运动

叶片处于加速旋转和匀速运转交替的工作状态，本文首先对已知叶片转速变化规律的旋转中心刚体—FGM 柔性梁系统特性进行分析。 在大范围运动已知的条件下系统的转动角速度变化规律可由式（6）所示：

式（6）中，ω0＝4 rad／s，Tt＝15 s，即加速旋转15 s 后梁的转动角速度达到4 rad／s，自此开始角速度维持不变。

建立3 种不同形式的简化叶片模型，即等截面实心梁（equal section solid beam，ESSB） 模型、等截面空心梁（equal section hollow beam，ESHB）模型、变截面空心梁（tapered hollow beam，THB）模型。 对这3 种模型的动力学特征进行对比。

以上3 种模型的尺寸数据如下：

（1）ESSB：L＝8 m，b1＝1.985 9 mm，h1＝3.675 9 cm；

（2）ESHB：L＝8 m，be＝2.808 5 mm，he＝5.198 5 cm，Bi＝1.985 9 mm，hi＝3.675 9 cm，gi＝0.293；

（2）THB：L＝8 m，be＝3.439 7 mm，he＝6.366 8 cm，Bi＝1.985 9 mm，hi＝3.675 9 cm，gi＝0.634。

当N与ΔT均为0 时，整个柔性梁均为陶瓷材料且不受热，为了证明本文的建模方法是正确的，设定Qc＝Qm并进行仿真，图3 为仿真结果，通过与杜超凡等［4］的对比两者的结果是一致的。

图3 模型验证仿真实验结果

大范围运动已知条件下3 种叶片模型尾部变形情况如图4 所示。 由图4（a）可见，等截面实心梁的尾部变形量最大，其次为等截面空心梁，与叶片实际结构接近的变截面空心梁尾部变形量最小。 由图4（b）可见，在大范围旋转角速度维持不变的状态下，柔性梁产生固定周期的振动，其中频率最高、振幅最小的是变截面空心梁，频率最低、振幅最大的是等截面实心梁。 由此说明柔性梁的结构对其动力学特性具有较大影响，因此必须根据实际结构创建系统模型。

图4 大范围运动已知条件下梁尾部变形情况

大范围运动已知条件下承受不同热冲击时柔性梁尾部变形情况如图5 所示。 由图5（a）可见，柔性梁内外部温差越大，其尾部的变形量越小，这是因为高温一侧的陶瓷材料热膨胀系数低，而温度相对较低的一侧金属材料膨胀系数高，且柔性梁的梯度材料分布是对称的，从而抑制了梁的横向弯曲变形，抑制能力也随着温差的增大而持续增强。 由图5（b）可见，大范围运动维持不变时柔性梁内外温差越大，热冲击的影响越明显，主要表现为梁的振动频率升高、周期变短，同时会产生高频振荡，而且抑制强度越高振动的幅度越大。

图5 不同热冲击作用时梁尾部横向总变形情况

设定柔性梁内外温差为ΔT＝300 K，在此条件下变截面空心梁尾部变形量及稳态响应受到功能梯度指数N的实际影响如图6 所示。 由图6（a）可见，柔性梁尾部的变形量会随着功能梯度指数N的递增而变大，且当N＜10 变化量较大，之后N继续增大时变形量仅发生较小的增长变化。 由图6（b）可见，稳态响应过程中振幅的变化是非线性的，随着N的递增振幅先增大后减小之后又持续增大，曲线的拐点分别为N＝3 和N＝7。

图6 N 的变化对梁尾部变形情况的影响

2.2 未知大范围运动

涡轮叶片工作过程中是在外力的驱动下旋转的，因此需要针对已经外力矩的状态进行动力学研究。 以时间为变量的外力矩函数表达式为式（7）所示［5］：

式（7）中，Tt＝10 s，τ0＝1N·m。

对于ESSB、ESHB、THB 这3 种模型，排除热冲击影响的大范围运动未知状态下的柔性梁尾部横向弯曲变形情况进行数据分析。 3 种柔性梁尾部变形量的差别相对于大范围运动已知状态下的变形量差别是一致的，ESSB 的尾部变形量最大，THB 的最小。 外力矩消失后，柔性梁开始周期性地持续振动，其中ESSB 的振动频率最低、振幅最大，而THB 的振动频率最高、振幅最小。

在大范围运动未知状态下，施加驱动力的外力矩较小，因此热冲击的驱动作用不能被忽略，实际上，此时叶片的旋转作用力是外力矩和热冲击作用耦合施加的，因此该状态下柔性梁尾部的变形应基于这种耦合作用进行研究。由此可见，由于温度场的作用柔性梁的变形产生了高频振荡，而且温度越高振荡幅度越大。 此时，梁的振动已不再呈现周期性，随着时间的推进，在热冲击的耦合作用下变形量会持续增大。

分析不同热冲击作用时大范围运动状态下中心刚体的角位移时程能够进一步分析计入热冲击作用后柔性梁不再进行周期性振动的原因。 随着内外温差的升高，外力矩消失后中心刚体旋转角位移的变化幅度有所增加，因此Tt＞10 s 后运动响应开始波动，且随着时间的推进振动愈加剧烈。 在大范围运动未知状态下外力矩与热冲击作用耦合驱动系统旋转，热力耦合使得运动的初始阶段就产生了高频振荡，即使撤去外力矩，在热冲击的作用下柔性梁仍保持了这种高频振荡的状态，而且振幅有所增加，并带动了刚体随之旋转，由此刚柔热耦合效应开始出现。

设定内外温差ΔT＝2 K，分析随着外力矩τ0的增加THB 尾部横向弯曲变形情况。 随着τ0的增加，热冲击作用所引发的振荡效应逐渐变弱，Tt＞10 s 后大范围运动保持稳定振荡也随之逐渐平稳，如果增大外力矩热冲击作用的影响会有所减小。 设定内外温差ΔT＝2 K，对功能梯度指数N对梁尾部横向弯曲变形的影响进行数值仿真分析。 柔性梁尾部变形量会随着N的递增而增大。 此时的高频振荡是在热冲击与弹性变形的耦合作用下产生的，N的变化改变了柔性梁的材料结构，进而改变了其振型与固有频率，分析可知，N增加到10 时外部作用对柔性梁的变形振荡影响较小。

3 结语

本文对旋转中心刚体—功能梯度材料梁刚柔热耦合动力学特性进行了研究。 基于物理变形研究了不同结构形式下柔性梁的动力学特性，对大范围运动已知状态下热冲击作用对梁的变形所产生的影响进行了分析，说明了大范围运动未知状态下热冲击与弹性变形结合的刚柔耦合作用对柔性梁所产生的振荡效应。 本次研究深入分析了高速旋转的中心刚体—FGM 梁的刚柔热耦合动力学特性，对于陶瓷材料转子叶片在高温状态下的运动强度研究具有一定的参考价值。