多维数据压缩存储方法研究

王 凯，张立博，李昌伟，李 帅，王 林

（中国绿发投资集团有限公司 北京 100010）

0 引言

多维数据压缩有助于传输和存储数据流。 为应对庞大且复杂的多维数据冗余信息［1］，应在保障重构数据精准性的基础上，最大程度提升数据压缩质量。 王鹤等［2］为实现电能质量数据高精度压缩目的，提出压缩存储配电网电能质量数据的方法，赵会群等［3］为保障数据存储精度，提出以密度划分为基础的多维数据存储方法，但两种方法的压缩存储效率较低。 为进一步提高多维数据的存储压缩效率，本文将在节约数据存储空间的基础上，以提高普适性、压缩效率和精准性为目的，探讨多维数据的压缩存储方法。

1 多维数据压缩存储方法

1.1 MVC 架构

MVC 技术根据视角间和视角内部的相关性提高多维数据压缩效率。 本文将以MVC 架构为基础建立多维数据压缩存储方法，具体见图1。

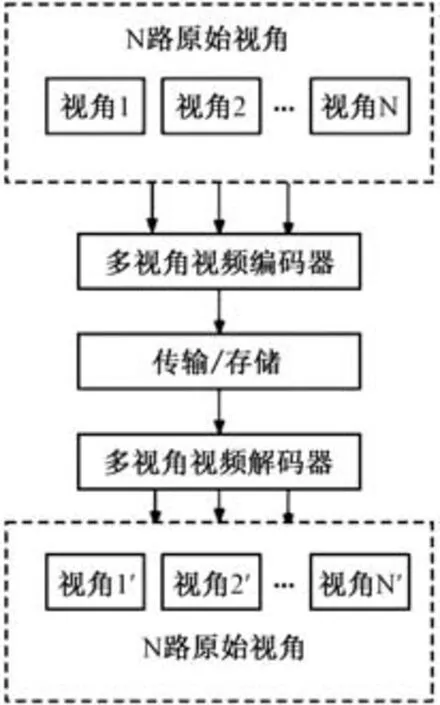
图1 MVC 架构

图1 中，多视角视频编码器单元采用多维矢量矩阵的MVC 压缩多维数据；传输／存储单元通过关系数据库方法存储压缩后的多维数据；多视角解码器对压缩数据实行反过程解码，以利于用户访问。

1.2 基于多维矢量矩阵的MVC 多维数据压缩方法

方法流程见图2。

图2 多维数据压缩流程

流程1：通过8×8（长×宽）分块采样处理原始数据以重组编码。

流程2：重组数据经多维离散余弦变换（discrete cosine transform，DCT）正交变换处理的操作为式（1）所示：

式（1）中：

LXX、均是偶数维，为多维DCT 操作算子；

T为正交变化次数；

fXY为数据源矩阵；

FXY表示变换后的多维系数矩阵。

以矢量X与Y划分变换输入后的数据源矩阵f8×8×8×8得式（2）：

变换表达公式为式（3）所示：

流程3：对编码变换后的系数矩阵数据进行非均匀量化以实现压缩编码操作，具体如下：多维数据经正交变换后的低频分量值多位于四维空间坐标原点附近，且该值与其距离原点的长度成反比例关系，多数高频分量值与0 无限接近，多维数据的量化公式为式（4）所示：

式（4）中：x，y，m，n＝0，1，2，…，7，表示坐标原点；αxymn表示多维数据排列表；q、p表示量化因子，－0.8 ≤p≤0.8、1 ≤q≤100；当p＝q＝0 时量化矩阵系数均为1，即未进行量化处理；量化因子值对量化效果有较大影响。 系数矩阵数据经压缩编码处理后可提升压缩质量。

流程4：通过差分编码预测数据量化后相关性较强的系数编码［4］。 具体如下：

假设变换数据后，与坐标原点距离最短的矩阵元素为直流分量DC，剩余则为交流分量AC［5］。 在n个8×8×8×n多视角数据里，各分块有8×n个直流系数。 因DC ＞AC，即DC有更强相关性［6］，因此在差分编码时选择保留交流分量AC而预测编码直流分量DC， 以此实现多维数据的有效压缩。 各分块间直流系数差分值在K个多视角数据分块中的计算方式为式（5）所示：

式（5）中：Diff表示差值。

流程5：对差分编码后的数据进行多维扫描处理，以使零元素数量增加。 计算公式为式（6）所示：

式（6）中：F为多维数据量化矩阵集合；H为常数，在N1×N2× …×Nm数据多维分块中，H取值范围0 ≤H≤N1＋N2＋…＋Nm － m；Bm取值范围为0 ≤H≤Nm －1；Bm函数为F（z），计算式为式（7）所示：

在8× 8× 8× 8 分块的多维数据中，基于多维扫描公式可得其表达式为式（8）所示：

式（8）中：a、b、c、d表示各维度坐标值，取值范围为0 ≤a≤7，0 ≤b≤7，0 ≤c≤7，0 ≤d≤7，且均为整数；u为多维扫描后数据，取值范围为0 ≤u≤28 且为整数。

将各坐标集中里的全部坐标值按小到大顺序进行排列，多维扫描坐标顺序排列结果为式（9）所示：

流程6：结束多维扫描后，多维数据中连续存在较多零元素，因此，仅需通过行程编码处理零元素。 在0 后为负数时，仅需保存一个0，并进行1 次重复；在0 后为整数时，则需采用（0，1）的形式保存数据，以尽可能避免解码时0 后的整数被解码为重复次数。

1.3 基于关系数据库的多维数据存储方法

将多维数据压缩后存储至关系数据库，具体流程见图3。

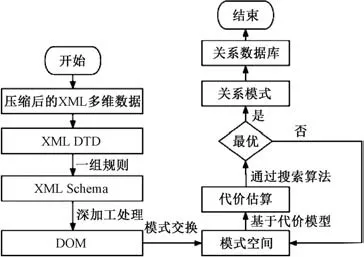
图3 关系数据库存储流程

具体步骤为：

步骤1：压缩后的可扩展标识语言（extensible markup language，XML）多维数据经数据类型定义后转换成XML DTD，随后再转换成XML Schema，以提高数据标准化程度。

步骤2：XML Schema 数据经深加工处理后生成数据对象模型；

步骤3：获取查询代价最小的模式S。 搭建含有各类模式的空间，并以哈希连接算法建立代价评估模型［式（10）］对各模式加以评估。

式（10）中：G1和G2表示多维数据压缩后的列表大小；P1和P2表示查询代价表的选择概率。

按照多维数据压缩后的实例信息获取第i个子图元素Ei的实例数量为｜Ei ｜，Ei属性列宽为Wi，按上述统计量计算第i个扩展子图Mi的值，计算式为式（11）所示：

式（11）中：j表示子图编号。

S模式根据连接操作顺序获取Ei所含的子图｛M1，M2，…，Ml｝ 以及与之相对应的｜Mk ｜、路径选择率Pk；操作代价和XML查询表达式以关系数据库加以连接，Ei查询代价以哈希连接算法代价模型加以计算，具体为式（12）所示：

式（12）中：k和l分别表示子图编号和数量。

S模式查询负载计算式为式（13）所示：

式（13）中：ω为查询代价权值。

步骤4：构建关系数据库。 通过爬山算法取得最优模式，再在映射规则基础上通过数据对象模型将最优模型映射为关系模型数据库。

2 实验分析

随机抽取7 组多维YUV 视频数据为对象，并根据小到大的数据量顺序加以排列，10 组实验数据的数据量范围为（1GB，10GB），Y 帧为亮度信息，U 帧和V 帧为颜色信息，以上述方法压缩存储试验数据。

2.1 压缩效果

所用压缩效果评价指标为峰值信噪比（PSNR） 和压缩比（Cr）。 随机选取1 组数据并压缩其全部分块，计算在量化因子p、q不同时的峰值信噪比和压缩比，以所得结果评价压缩性能，详见表1。

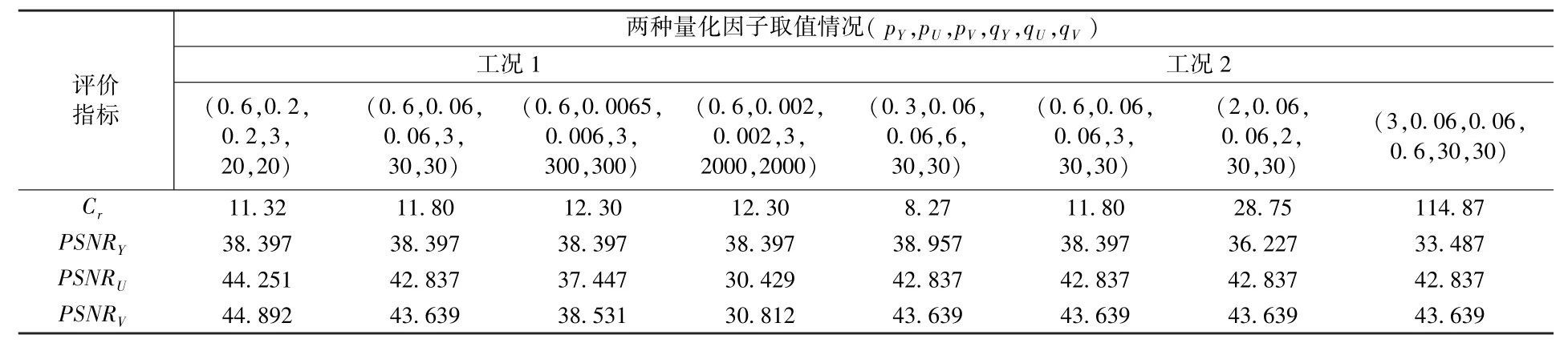
表1 不同量化因子下的峰值信噪比和压缩比

如表1 所示，工况1 中，固定pY及qY时的，峰值信噪比固定不变；在减小pU并增加qU时，峰值信噪比有所减小；V 帧与U 帧的峰值信噪比基本一致；在减小V 帧与U帧的峰值信噪比并小幅提升数据压缩比时，数据压缩效果一般。 工况2 中，固定U 帧量化因子和V 帧量化因子，但改变Y 帧，此时随pY增加，qY逐渐降低，峰值信噪比出现较小降幅但压缩比大幅提升。 结果表明：固定V 帧与U帧量化因子时，适当提高Y 帧量化因子值可在小幅度减小峰值信噪比的条件下，大幅提高压缩比，提高多维数据压缩性能。

以王鹤等［2］提供方法为方法1，以赵会群、李春良［3］提供方法为方法2，与本文所提供方法进行试验对比，通过三种方法分别压缩全部分块，所得结果见表2。

表2 三种方法压缩时间 单位：s

从结果看，三种方法的压缩时间随数据量的增加而不断增加，但文中所提供方法所需压缩时间显著少于其他两种方法，即本文所提供方法所需压缩时间较短，压缩效果更好。

2.2 存储效果

三种方法的存储效率试验结果见图4。

图4 三种方法存储效率测试结果

从结果看，越多数据量下三种方法的存储消耗时间也越长，但本文方法存储消耗时间较少，增幅较小，表明本文方法存储效率较高。

3 结语

为提高数据压缩存储效果，本文利用MVC 架构搭建了多维数据的压缩存储方法，从对比实验结果看，所提出方法有较高的压缩存储效率，有一定的推广应用价值。MVC 架构发展空间大，后续可从多维矢量操作算子的角度出发优化扫描和量化方法，提高行程编码性能。