参数冻结精细指数积分法在非线性车桥耦合振动分析中的应用1)

张 宇 李韶华 任剑莹

* (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

† (石家庄铁道大学工程力学系,石家庄 050043)

** (石家庄铁道大学河北省工程力学基础学科研究中心,石家庄 050043)

引言

在桥梁系统众多力学问题中,车桥相互作用问题是一个长期的热点课题[1-6].其核心在于如何准确地预测车桥耦合振动行为.当车辆在桥梁上运行时,车辆和桥梁之间是相互作用和互相影响的,这称之为车桥耦合振动.车桥耦合振动行为的研究可为桥梁结构的设计、运营、维护和管理提供必要的理论基础、分析方法以及评估手段,具有非常重要的工程应用价值[3].关于车桥耦合系统动力学问题的研究,早期研究将移动的车辆对桥梁施加的力建模为移动载荷[7-8].在这种模型中,移动的车辆和桥梁之间不存在动态耦合关系,车辆载荷只是移动在桥面上的外部激励.然而,当车辆模型中考虑惯性力时,桥梁和车辆在接触点处的响应是耦合的,即构成车桥耦合系统[9].且由于车辆位置随时间的不断改变,描述车桥耦合系统的动力学方程组具有时变特性[10-11].通常情况下,即使是线性时变系统也很难得到精确解,因此各种近似方法被应用于获得车桥耦合系统的动力学响应.

车桥耦合系统通常采用有限元法[12-16]或模态叠加法[17-19]进行建模和分析.通过相应方法得到时变常微分动力学方程以后,进一步采用直接积分法进行求解,主要有线性加速度法、Wilson 法和Newmark法等[20].Zhu 等[21]采用精细积分法计算了移动载荷通过连续梁桥时的动力学响应.Zhai[22]基于Newmark法发展了两种高效的显式数值积分方法,提高了大规模计算时的效率和精度.Stoura 等[23]提出了一种求解车桥耦合动力学模型的动态划分方法,该方法如结合适当的数值格式可显著降低计算量.处理各种时变系统动力学问题时,Newmark 法[10]和Runge-Kutta 法[24]是应用较多的数值方法.此外,控制问题中经典的时间参数冻结技术也被应用于慢时变系统动力学问题[25].最近,Ge 等[26]针对时变动力学系统的计算问题,提出了求解车桥耦合系统受迫振动的时间参数冻结方法,该方法可较好地处理线性时变车桥耦合问题.

在车桥耦合问题的计算中,为了数值计算的准确性,在某些工况下需考虑非线性因素,如桥梁跨度大,当载荷作用下产生大变形时的几何非线性[27].当考虑非线性因素时,描述车桥相互作用问题的动力学方程组具有典型的时变、非线性特性,对其高效、精确的求解具有重要的意义.

1994年,钟万勰[28]针对线性常系数微分方程问题的计算,提出了精细积分法,该方法在求解指数矩阵时用矩阵加法代替乘法,巧妙地避免了舍入误差.由于其优异的数值特性,近年来精细积分法得到了广泛的研究和应用[29-32],并发展出了增维精细积分法[33]、广义精细积分法[34]、辛精细积分法[35-36]和快速精细积分法[37]等方法.针对半线性微分方程问题,近年来发展了多种指数积分方法及其相应的计算格式[38],在处理高振荡、刚性问题中得到了良好的应用[39-40].邓子辰等[41]结合精细积分法和指数积分法,提出了精细指数积分法,并将其应用于卫星编队飞行动力学问题中弱非线性方程的求解,但并未考虑时变问题.

车桥耦合动力学问题解析求解难度大,通常采用数值积分方法进行求解,如经典的Newmarkβ法、Runge-Kutta 法.但是这两种方法受稳定性影响较大,数值积分步长需选取较小,这会增加计算时间,降低计算效率.且这些算法本身具有一定的数值耗散性,在长时间数值积分后可能会导致计算结果的失效.因此,本文针对上述问题,将精细指数积分法与时间参数冻结技术相结合,提出一种新的计算方法——参数冻结精细指数积分法,并将其拓展应用于车桥耦合系统动力学问题的求解中.充分发挥不同方法的特点和优势,使其能够高效、精确地求解具有时变、非线性特性的车桥耦合动力学方程组,预期可为车桥耦合问题的动力学仿真计算提供一种新的方法.

1 考虑桥面铺装层的车桥耦合模型

考虑汽车通过跨度为L的桥梁,建模时桥梁采用包含铺装层和桥体的层合梁模型,汽车采用车桥耦合振动问题建模中常用的两自由度1/4 汽车悬架模型[10,24,42].车桥耦合模型示意图如图1 所示.

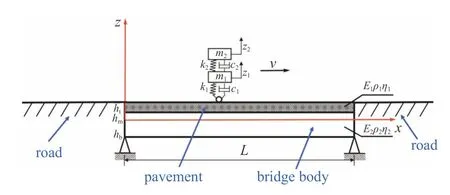
图1 车−桥面铺装层−桥耦合模型Fig.1 Vehicle-pavement-bridge coupled model

考虑汽车自桥梁左端向右以匀速v行驶,1/4 车模型有两个描述垂向振动的动力学方程[10]

其中m1和m2分别为非簧载质量和簧载质量,z1和z2分别为非簧载质量位移和簧载质量位移,k1和k2分别为轮胎和悬架刚度系数,c1和c2分别为轮胎和悬架阻尼系数,w1为车桥耦合振动引起的车轮与桥面接触点处桥面的二次位移激励值.

车轮与桥面接触的动态轮胎力可表示为

基于达朗贝尔原理,考虑图1 中的具体层合梁模型,梁的振动方程可给出如下

其中 ρ为梁材料等效密度,ρ1和 ρ2分别为桥面铺装层和桥体的密度,ht,hm和hb分别表示铺装层上表面、铺装层与桥体连接面和桥体下表面的位置坐标,A为梁横截面积,w表示梁的横向位移场,M为弯矩,σx为梁轴向应力,F(x,t)为梁横向外载荷,符号(.)表示对时间t求导,符号(')表示对空间x求导.

当式(6)做积分运算时,z值0 点在层合梁中性轴处,即图1 中x轴位置.因此,需根据桥面铺装层和桥体具体参数确定ht,hm和hb的坐标.假设铺装层厚度为h1,桥体厚度为h2,桥面铺装层和桥体的弹性模量比值为

其中E1和E2分别表示桥面铺装层和桥体的弹性模量.中性轴距离上边缘距离hpt和下边缘的距离hpb以及ht,hm,hb的坐标分别为

桥梁结构自身具有一定的对外界能量耗散和减振能力,其对振动能量的耗散能力可用黏性阻尼系数来体现[43].本文桥梁建模考虑了Kelvin 黏弹性理论以及几何非线性特性,梁轴向应力−应变关系和应变−位移关系可给出如下

其中 εx为梁轴向应变,η为黏性阻尼系数.

将式(3)、式(6)、式(11)和式(12)代入式(4)可以得到

其中 δ为狄拉克函数,满足关系

b为梁宽度,η1,η2分别表示铺装层和桥体的黏性阻尼系数.式(13)中如不考虑梁几何非线性,则 ξ2和 ξ3等于0,如不考虑梁的黏弹性,则 ξ4等于0.

采用伽辽金法可将偏微分方程(13)进行简化,本文考虑梁两端为简支边界条件,则梁横向位移函数可表示为

其中 sin(iπx/L)为梁简支边界条件下的第i阶模态函数,qi(t)为梁振动的第i阶广义位移.对于受移动载荷作用的简支梁桥,其一阶模态函数对横向振动起决定性作用[8].因此,本文选取了桥梁一阶模态进行研究,即N= 1.应用伽辽金法,将式(16)代入式(13),乘以第1 阶模态函数并沿梁长积分,则可给出描述梁横向振动的非线性常微分方程如下

整理式(1)、式(2)和式(17),即为本文中描述车桥耦合振动的动力学方程组,其中广义位移向量为X=[z1,z2,q1]T

通过观察式(19)可以发现,由于系数中显含时间t,且由于 ψ3和 ψ4的存在,该动力学方程组为时变和非线性的,很难得到解析解,通常采用数值方法进行求解.式(19)可整理成矩阵的形式,如下

系数矩阵M,C,K,F分别为质量矩阵、阻尼矩阵、刚度矩阵和载荷列阵.为便于编程计算,式(19)中的非线性项写入式(20)载荷列阵F中,在每一数值积分步,可采用上一积分步的计算值近似求解非线性项.式(20)即可采用常规数值积分方法进行求解,如经典的Newmark-β法.

2 参数冻结精细指数积分方法的应用

将方程组(19)降阶为一阶动力学方程组,可表示为如下形式

如能精确求解矩阵A,即可由式(25)计算出每一离散时间步的数值解uk.对于矩阵A的求解,可采用精细积分法[28],其思路是利用指数函数的加法原理,将时间步长分为 2n等分,如令 Δt=τ/2n,则有[41]

由于 Δt=τ/2n是一个极小的时间段,如对exp(LCΔt)进行泰勒展开,取其前5 项就能达到足够的精度,即

其中,I为单位矩阵,A1是一个很小的矩阵.为避免计算过程中的舍入误差,由式(26)和式(27)有

如定义矩阵序列

则由式(28)可得递推关系如下

由式(29)求得矩阵序列An+1的值,代入式(30),与I阵相加即可求得矩阵A的值.此过程中,利用了指数函数的性质,巧妙地运用加法代替乘法,避免了严重的舍入误差,使算法具有很高的精度,通常取n=20即可保证良好的数值性能.且由于在计算中的每一时间步 τ内插入了 2n个点,即使步长 τ值取的较大,也不影响计算的精确性[44].

精细积分法在计算一般的常系数齐次线性微分方程时,能够达到极高的精度.但车桥耦合问题的动力学方程组系数矩阵具有时变性,即式(22)中L(t)为时变系数矩阵.此时可以采用时间参数冻结的思想,基于时间参数冻结技术的基本概念,在每一个离散步长计算间隔内,假设L(t)为常数矩阵,则系统定常,即可应用精细积分法求得每一时间区间内的响应.如式(25),在计算uk+1的数值结果时,依据平均的思想,可假设

式(31)中由于在每一离散步内引入了近似,因此,当时间间隔 τ越小时,近似解越接近于精确解.

进一步考虑非线性部分的处理,式(22)中对时间离散后,解的形式可表示为

其中,右端第1 项为线性部分,即采用上述参数冻结后的精细积分法进行求解,右端第2 部分积分项为杜哈梅积分.对式(32)采用不同的方法求解,可得到不同的指数积分法,应用较多的是指数Runge-Kutta法,本文即采用指数Runge-Kutta 法进行计算.s级的指数Runge-Kutta 法可表示为[41]

其中,aij(LCτ)和bi(LCτ)为待定矩阵,ci为待定常数.aij(LCτ)和bi(LCτ)可以根据积分因子法按照如下的规律给出[41]

其中,系数aij,bi,ci与经典Runge-Kutta 法中系数相同,即每一种经典Runge-Kutta 法都对应有一种指数积分法.式(33)中关于指数矩阵的求解均可由精细积分法进行精确计算,这种将精细积分法和指数积分法结合得到的方法称为精细指数积分法[41].本文基于精细指数积分法与时间参数冻结技术,创新性地将二者结合到一起,提出参数冻结精细指数积分法,并将其应用于车桥耦合动力学问题的求解中.参数冻结精细指数积分法的计算重点在于每一迭代步中对时变矩阵L(t)的近似处理和对指数矩阵A的精细积分求解,其数值计算格式容易构造,且可以方便地处理时变、非线性问题.

3 算例分析

如前文所述,每一种Runge-Kutta 法都可构造相对应的指数积分法,本文基于简单的四级四阶显式Runge-Kutta 法(RK4-4)[41]构造了相应的参数冻结精细指数积分格式(FPEI4-4).

首先,为验证本文车桥耦合模型及理论计算的有效性,基于车桥耦合实验平台,进行了实验测试.用于测试的实验装置参数为: 跨度 3 m的两端简支实验桥,采用空心铝板制作,其密度为 2700 kg/m3,横截面积为 9.24×10−4m2,弹性模量为 7 0 GPa,惯性矩为 2.67×10−7m4; 实验小车质量为 2 kg,轮间距为9.5×10−2m,车速为 0.2 m/s.实验时在桥跨中布置位移传感器,利用ARTDAQ 信号采集显示软件进行数据采集,采样频率为1000 Hz.实验测试模型及测试现场如图2 和图3 所示.图2 中,1 为西门子V90 伺服电机,2 为传动齿轮,3 为传动链条,4 为挡板,5 为小车,6 为实验桥支座,7 为桥板,A 和C 为辅助梁,B 为实验梁.

图2 实验测试模型示意图Fig.2 Schematic diagram of experimental test model

图3 实验测试现场图Fig.3 Diagram of experimental test site

实验测试结果(test result,TR)与基于1/4 车−桥耦合模型的FPEI4-4 格式数值计算结果进行了对比,FPEI4-4 格式选取了时间步长为 τ=1.0×10−3s,结果如图4 所示.

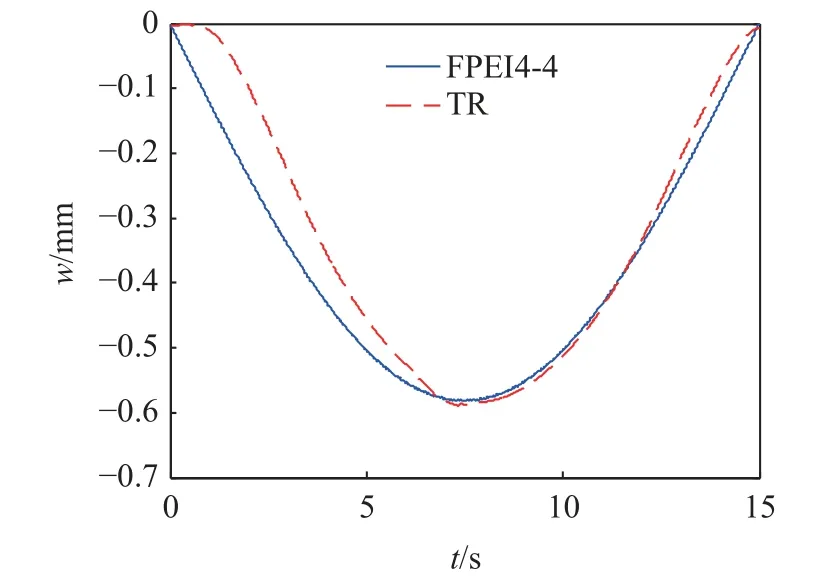
图4 数值计算和实验测试的跨中挠度结果Fig.4 The numerical and test results of mid-span deflection

从图4 中可以看出,实验测试和数值计算结果的演化趋势基本吻合,挠度峰值误差很小.图4 中的结果对比能够说明本文理论建模和数值计算的有效性,其具有实际应用价值.此外,图4 中数值计算与实验测试结果误差主要来源于车辆简化模型的误差,以及实验装置的制作误差、外界环境因素等.如采用更加精细化的车辆模型,可减小理论计算和实验结果的误差,但即使是选用简单的1/4 车辆模型进行理论分析,其依然能够较为精确地预测挠度峰值结果.

理论结果计算的精确性主要取决于所建立的车桥耦合动力学模型的精细化程度,本文所提算法主要关注于对已建立的动力学微分方程的高效求解.后文应用所构造的FPEI4-4 格式与经典的Newmark-β算法进行了数值计算,对比了2 种算法在求解车桥耦合动力学方程组(19)时的数值特性.

数值模拟中采用了重型载货汽车模型,具体车辆参数见表1[45],表2 给出了桥的参数,包括桥面沥青铺装层参数和桥体参数.

表1 汽车参数Table 1 Vehicle parameters

表2 桥面沥青铺装层和桥体参数Table 2 Pavement and bridge parameters

由于文中车桥耦合动力学方程组具有时变和非线性的特性,难以得到解析解,因此选用了小步长下高精度的二级4 阶隐式辛Runge-Kutta 算法(SRK2-4)的计算结果作为参考.

s级隐式Runge-Kutta 法的一般格式为[46]

式(35)中当其系数满足以下条件时为辛Runge-Kutta 法

当系数bij和ci取不同值时,可得到不同的辛Runge-Kutta 格式.比较常用的SRK2-4 积分格式,其系数表示如下

同时,为了能够说明针对动力学微分方程模型数值计算结果的有效性,构造了本文模型中桥梁位移的近似解析解.基于文献[47]中的思路,式(19)中第3 个方程可简化为

由于本文工况中广义位移q1值和广义速度1值较小,非线性项对振动的影响较弱,若略去两项非线性项,并引入参数

则可得到桥梁广义位移q1的近似解析解(approximate analytical solution,AAS)为

图5 给出了车速分别为10 和50 m/s 时,近似解析解、FPEI4-4 格式和SRK2-4 格式计算的桥梁跨中挠度的结果,其中计算时FPEI4-4 格式选取了大时间步长 τ=1.0×10−2s、SRK2-4 格式选取了小时间步长 τ=1.0×10−4s.

图5 近似解析解、时间步长为 τ=1.0×10−2 s 的FPEI4-4 格式和时间步长为 τ=1.0×10−4 s 的SRK2-4格式计算跨中挠度结果Fig.5 The results of mid-span deflection calculated by analytical approximate solution,FPEI4-4 scheme with τ=1.0×10−2 s and SRK2-4 scheme with τ=1.0×10−4 s

从图5 中可以看出,每种工况下3 条曲线的演化趋势相同,车速较小时(v= 10 m/s)曲线吻合得更好,这充分体现了数值计算结果的有效性.此外,从局部放大图中可以看出,FPEI4-4 格式和SRK2-4 格式的计算结果始终几乎重合,而与近似解析解有一定的偏差.这是因为近似解析解忽略了耦合因素和非线性因素,而数值格式是直接基于原微分方程(19)计算的原因.

从图5 中的对比也可以体现出,当车速较大时,车桥耦合和非线性因素对桥梁的振动特性影响更为明显.由于所构造的近似解析解忽略了部分因素,不能严格地反应振动响应的演化趋势,因此后文为更好地体现所提出方法的数值特性,选用了SRK2-4格式的数值计算结果进行参照对比.

假设车速分别为10 和20 m/s,利用SRK2-4 格式计算了文中车桥耦合动力学方程组.图6 中给出了当选取时间步长分别为 τ=1.0×10−4和 1.0×10−5时,SRK2-4 格式计算的桥梁跨中挠度结果之差.

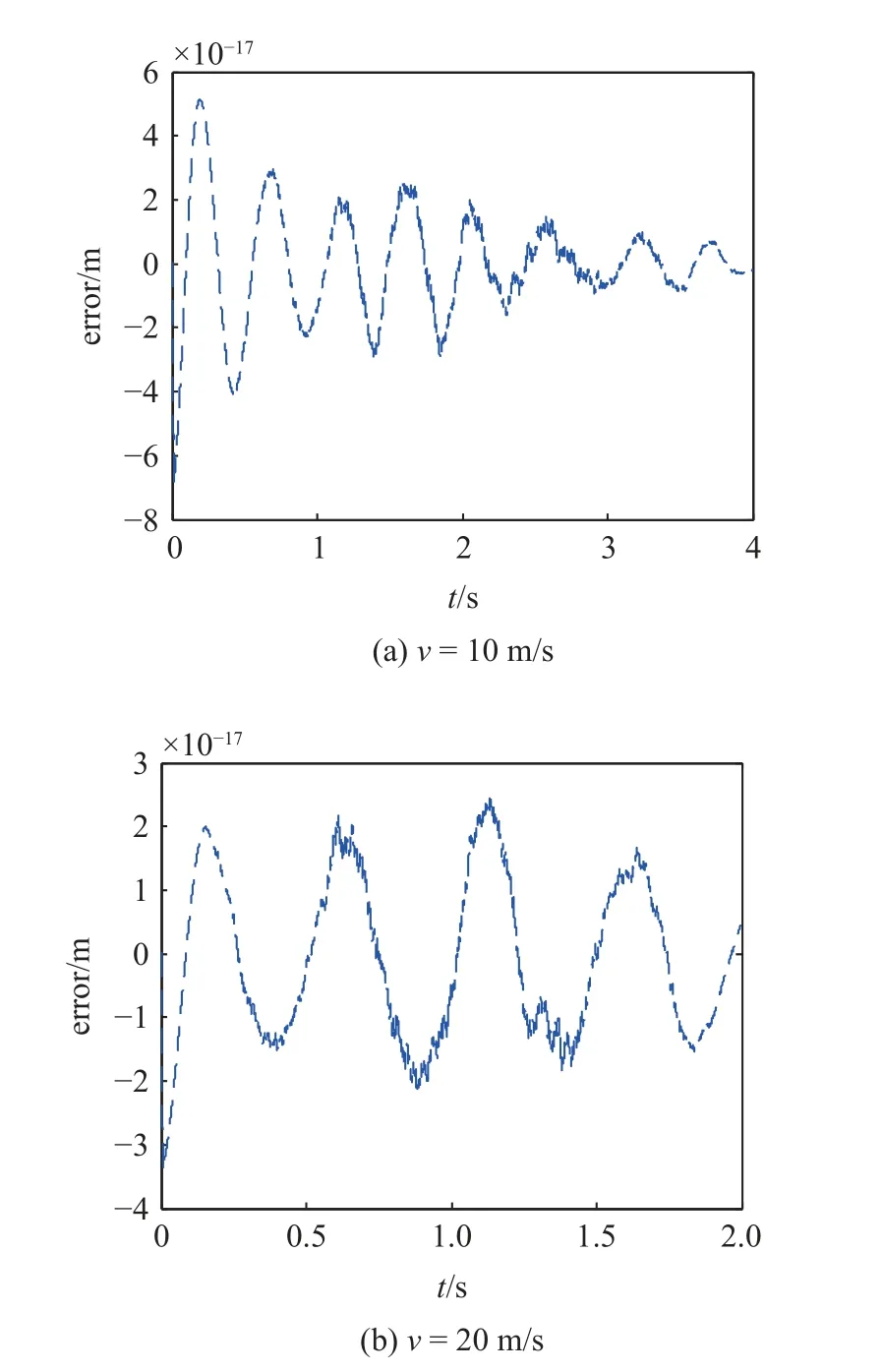
图6 时间步长为 τ=1.0×10−4 s 和 τ=1.0×10−5 s 时SRK2-4 格式计算跨中挠度结果之差Fig.6 The difference between the results of mid-span deflection calculated by SRK2-4 scheme under time step τ=1.0×10−4 s and τ=1.0×10−5 s

在数值积分运算中,当选取数值积分步长越小时,数值计算结果越收敛于解析解.从图6 中可以看出,选取较小时间步长为 τ=1.0×10−4和 1.0×10−5时,两种车速工况下的数值结果差值已经非常小,达到了10−17m量级,此时已非常接近解析解.因此,可将选取小步长下的SRK2-4 格式计算结果作为参照解.由于SRK2-4 格式为隐式格式,为提高计算效率,本文选用了积分时间步长为 τ=1.0×10−4s时的SRK2-4 格式进行数值计算.后文中的误差均表示不同时间步长下相应算法的计算结果与时间步长为τ=1.0×10−4s时SRK2-4 格式计算结果的差值.

3.1 不同数值积分时间步长时的计算结果对比

对比了选取不同时间步长时,应用FPEI4-4 格式和Newmark-β算法计算文中车桥耦合模型的精度.选取车速为相对较快的20 m/s 过桥,以时间步长为 τ=1.0×10−4s时的SRK2-4 格式计算结果作为参照解,应用本文构造的FPEI4-4 格式和经典的Newmark-β算法得到了桥梁跨中挠度计算结果与参照解的误差,如图7 所示.

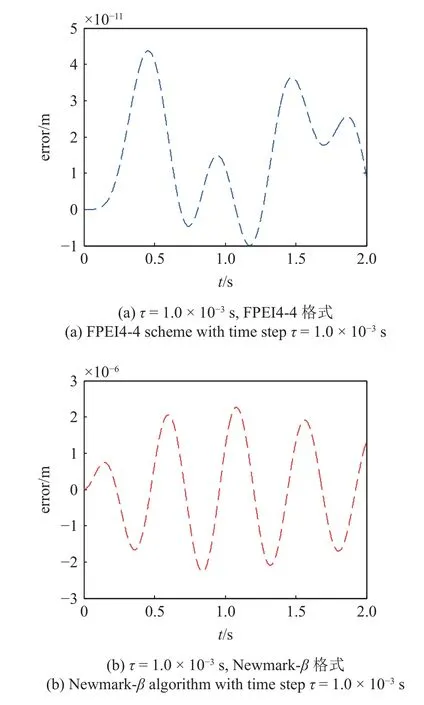
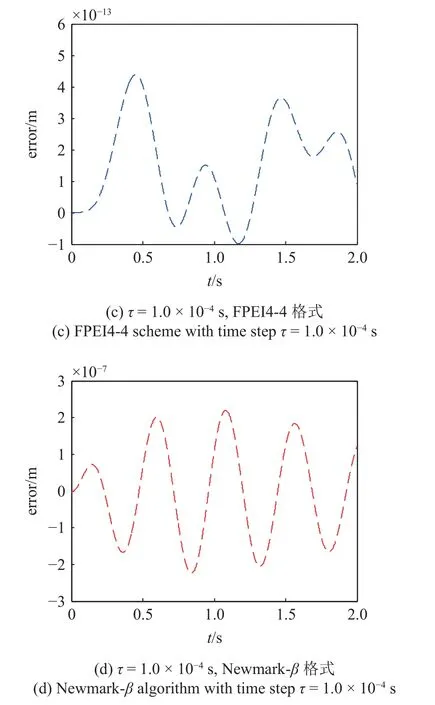
图7 FPEI4-4 格式和Newmark-β 算法求解跨中挠度计算误差Fig.7 The numerical errors of mid-span deflection calculated by FPEI4-4 scheme and Newmark-β algorithm

从图7 可以看出,在选取时间步长为 τ=1.0×10−3s时,FPEI4-4 格式与参照解的误差在10−11m量级,在选取时间步长为 τ=1.0×10−4s时,与参照解的误差达到了10−13m 量级.作为一种显式计算格式,相比于相同数值积分步长时的经典Newmarkβ算法,本文所构造的FPEI4-4 格式具有明显更小的误差、更高的计算精度.

当进一步增大时间步长,取时间步长为τ=5.0×10−3s时,如图8 所示,Newmark-β算法计算结果已出现明显的数值发散现象,导致计算失败.如继续增大时间步长,Newmark-β算法计算结果会直接发散.而从图8 中还可以看出,即使将时间步长增加到很大的 τ=1.0×10−1s时,FPEI4-4 格式同样能给出较好的计算结果,这体现了该计算格式优异的数值特性.由于精细积分法自身的特性,FPEI4-4 格式即使选取大时间步长,也不会出现数值发散现象,而大步长下的数值误差主要来源于对系数矩阵L(t)参数冻结时引入的误差.

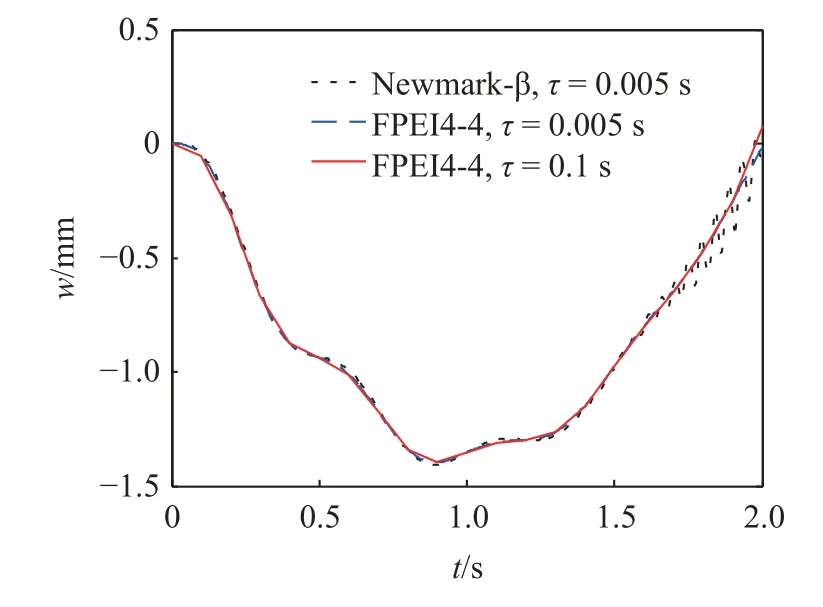
图8 FPEI4-4 格式与Newmark-β 算法得到的桥梁跨中挠度结果Fig.8 The results of mid-span deflection calculated by FPEI4-4 scheme and Newmark-β algorithm

表3 进一步给出了2 种算法在选取不同时间步长时的计算时间和最大误差.从表3 中可以看出,Newmark-β算法作为一种经典的动力学方程数值求解方法,在相同的小时间步长下,其比FPEI4-4 格式的计算速度更快.而FPEI4-4 格式则具有明显的精度优势.此外可以看出FPEI4-4 格式具有更好的数值稳定性,能够选取较大的积分时间步长来加快计算速度,且在大步长下仍能保持较好的计算精度,而在大步长情况下Newmark-β算法将直接发散使得计算失败.如选取 τ=1.0×10−2s的FPEI4-4 格式与τ=1.0×10−4s的Newmark-β算法对比,FPEI4-4 格式在计算时间(0.031098 s)远小于Newmark-β算法(0.869262 s)的情况下,其最大误差仅约为Newmarkβ算法的1/50,具有更好的效率和精度优势.

表3 Newmark-β 算法和FPEI4-4 格式计算跨中挠度对比Table 3 Comparison of mid-span deflection calculated by Newmark-β algorithm and FPEI4-4 scheme

后文中为了说明本文FPEI4-4 格式的优势,直接选取了大时间步长进行计算,即取 τ=1.0×10−2s,在该时间步长下传统的Newmark-β算法将直接发散.

3.2 数值积分的长时间稳定性

为了更好地体现本文所构造格式的长时间数值特性,进行了长时间的数值积分运算结果对比.

首先关注长时间振动解的稳定性质.因车在桥上时间较短,当车下桥以后,由式(19)描述的车桥耦合作用将消失,其后桥将做有初位移和初速度的自由振动,其初位移和初速度由车下桥时桥振动位移和速度给出,其值均不大,靠近相图(0,0)点.

关注于桥自由振动阶段,此时动力学方程为

如令x=q1,y=,可得一阶微分方程组为

原点(0,0)为满足式(43)的奇点,是式(43)的零解.

如考虑桥梁黏性阻尼,式(43)的线性近似方程组特征方程为

代入数值可得特征方程两个根均具有负实部,可知零解x=y=0为渐近稳定的,此时奇点(0,0)为稳定焦点,相图中的轨线表现为盘旋趋近原点(0,0).

如忽略桥梁黏性阻尼,则线性近似方程组特征方程为

代入数值可得特征方程的2 个根均为纯虚根,此时奇点(0,0)为中心型奇点,零解为稳定但非渐近稳定的,其相图中的轨线表现为以(0,0)为中心的圆.

综上所述,由于初始条件趋近(0,0)点,且(0,0)点为稳定奇点,因此长时间积分计算的解是稳定的.这里忽略了桥梁黏弹性特性,则汽车在过桥以后,桥梁将做幅值相等的无耗散往复自由振动.

首先给出了Newmark-β算法在选取数值积分步长 τ=1.0×10−4s时计算的跨中挠度时程曲线,以及跨中挠度−速度相图,如图9 所示.算例中选取车速为20 m/s,汽车下桥后继续计算了100 s 的桥梁自由振动,计算耗时为35.948393 s.

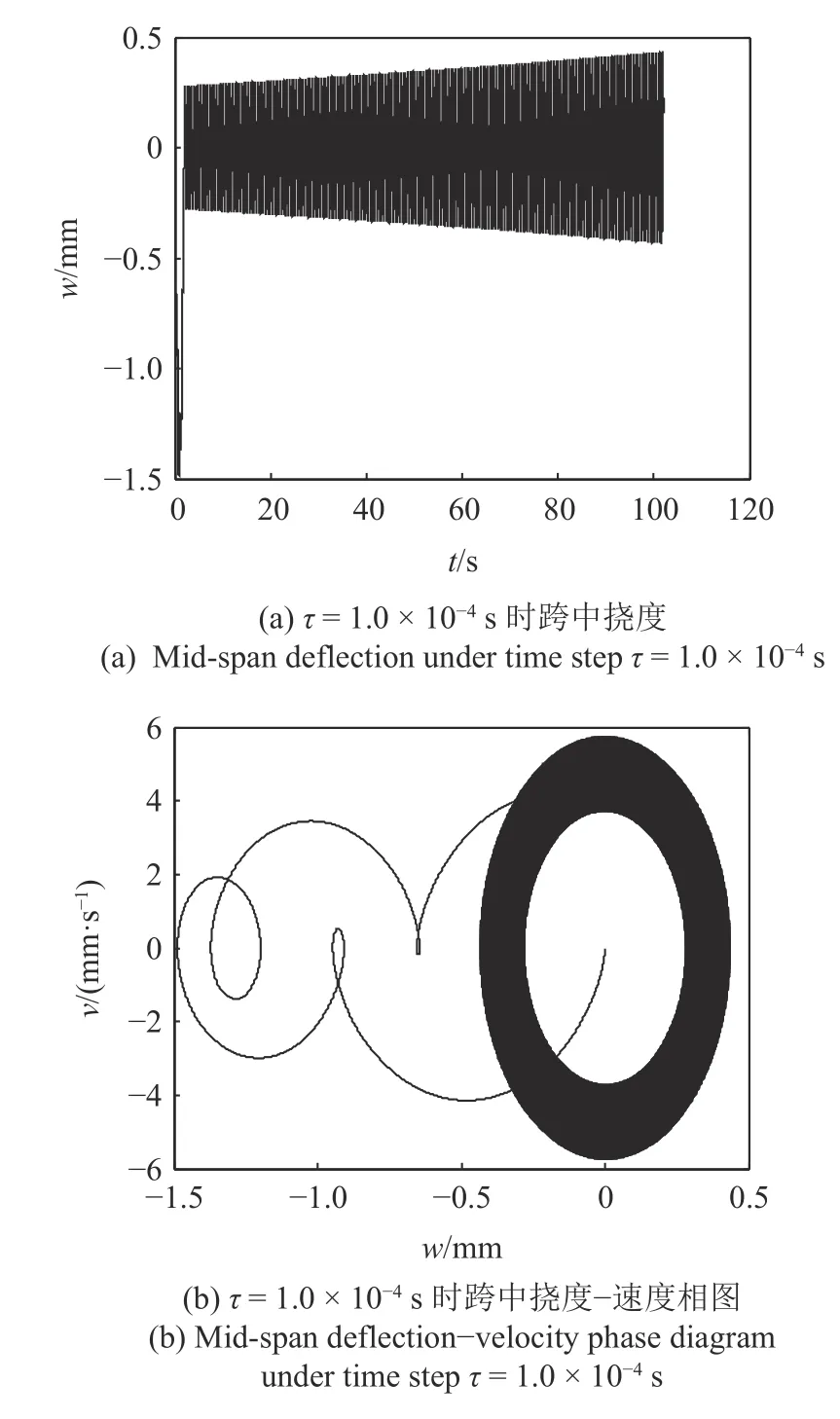
图9 Newmark-β 算法的计算结果Fig.9 The calculation results of Newmark-β algorithm

从图9 中可以看出,即使选择了较小的时间步长( τ=1.0×10−4s),Newmark-β算法在长时间积分时,仍具有明显的数值耗散性.图9(a) 中显示,Newmark-β算法计算的汽车下桥后桥梁自由振动数值解具有发散的特性,长时间数值积分后会导致计算结果的失效.从图9(b)中也可以看出,在自由振动的周期阶段,跨中挠度−速度相图表现出了明显的发散现象.

选取相同的工况,图10 进一步给出了显式FPEI4-4 格式计算的桥梁跨中挠度以及挠度−速度相图的数值结果.数值积分计算时,选用了大时间步长τ=1.0×10−2s.

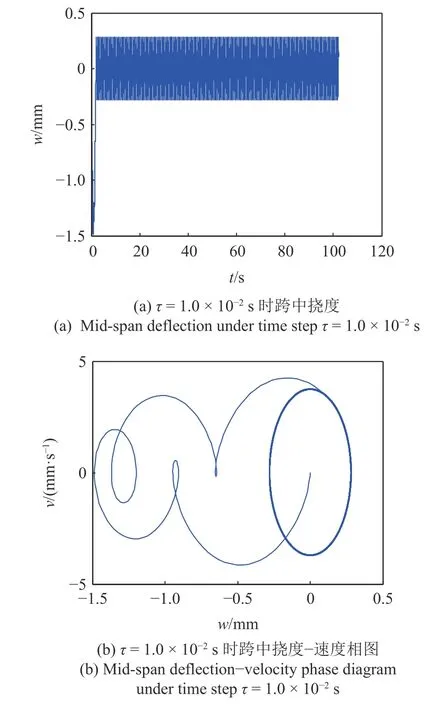
图10 FPEI4-4 格式的计算结果Fig.10 The calculation results of FPEI4-4 scheme

从图10 中可以看出,即使选择了较大的时间步长,本文所提出的显式FPEI4-4 格式仍具有良好的数值特性,数值计算结果保持了长时间的数值稳定性,无发散迹象.由于此时零解为稳定但非渐近稳定的,其相图中的轨线表现为以(0,0)为中心的圆,如图10(b)中右侧所示,图10(b)左侧为车桥耦合初始阶段的轨线.由于精细积分法自身的特点,可以选取大时间步长进行数值积分运算,本算例中步长取为τ=1.0×10−2s,计算耗时仅为1.370017 s.文中虽然对时变矩阵L(t)在每一离散步进行了参数冻结近似,但结果显示在选取较大步长时依然具有良好的数值精度.通过与时间步长 τ=1.0×10−4s时的隐式SRK2-4格式计算结果对比,自由振动阶段的最大误差稳定维持在 1.38×10−6m量级.本文选取的计算模型矩阵维数较小,如当处理高维时变车桥耦合动力学问题时,选取大步长所带来的计算效率优势将更加明显.

3.3 不同时变程度的计算结果对比

由于汽车为移动载荷,导致车桥耦合动力学方程组具有时变性,由式(22)可以看出,当汽车和桥梁参数确定的情况下,系数矩阵时变的快慢和车速v直接相关.本文数值格式构造时,在每一离散步长时间间隔内对时变矩阵L(t)进行了参数冻结处理,将时变系数矩阵近似为每一离散步内的常数矩阵.这种近似带来的误差和矩阵时变的快慢以及步长的选取有关,因此进一步分析了系数矩阵具有不同时变程度时(不同车速)所构造的FPEI4-4 格式的数值特性.

图11 给出了选取大时间步长为 τ=1.0×10−2s时,不同车速下FPEI4-4 格式求解的桥梁跨中挠度与参照解的计算误差.从图11 中可以明显看出,车速越快,FPEI4-4 格式计算结果与参照解的计算结果差别越大.当车速为10 m/s 时,最大差值为 7.754 9×10−10m; 车速为20 m/s 时,最大差值为4.409 3×10−9m; 车速为50 m/s 时,最大差值为 1.432 6×10−8m.由于车速与时变矩阵变化快慢直接相关,车速越大,参数冻结引起的误差就会越大,这符合预期.但即使在车速为50 m/s 时(时速为180 km/h),误差仍可保持在10−8m 量级,而此车速下跨中挠度的最大值为1.743 2×10−3m,跨中计算结果仍是可接受的.因此本文所构造的FPEI4-4 格式同样适于计算快车速、快时变问题,具有实际应用性.

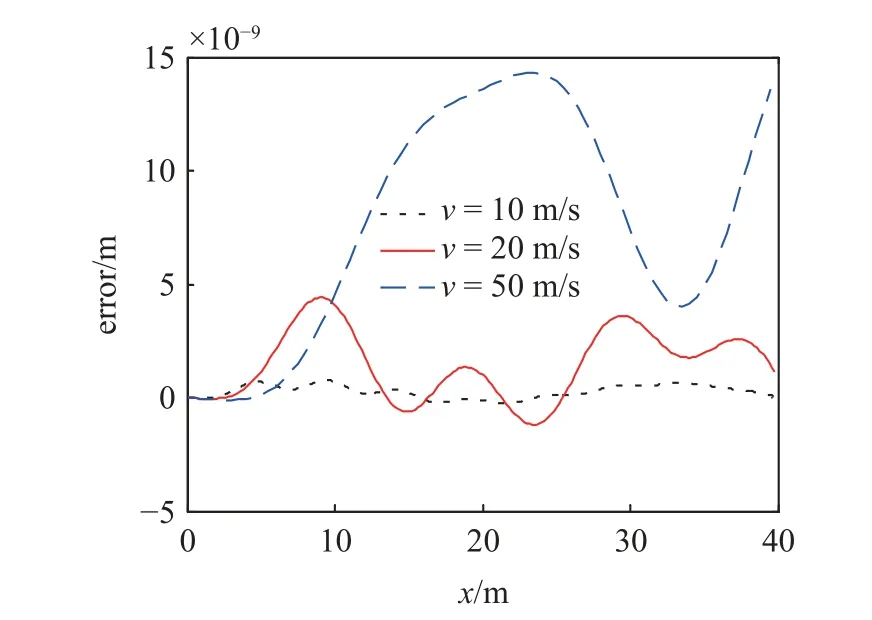
图11 τ=1.0×10−2 s,不同车速时FPEI4-4 格式求解跨中挠度计算误差Fig.11 The numerical errors of mid-span deflection calculated by FPEI4-4 scheme under different vehicle speeds with time step τ=1.0×10−2 s

3.4 时变系数矩阵 L(t)冻结方式的对比

本文应用的数值格式在处理时变问题时,采用了参数冻结技术,对每一积分步的时变系数矩阵进行了近似处理,本节对比分析选取不同的近似方式时对数值计算结果的影响.下式列举了每一离散步对时变矩阵L(t)进行参数冻结的3 种方式,本文基于平均的思想,应用的近似矩阵LC1.在此,对比分析分别选取LC1,LC2和LC3时的数值特性

图12 给出了选取不同近似矩阵时,应用显式FPEI4-4 格式计算的桥梁跨中挠度和挠度−速度相图的数值结果,计算时选取车速为20 m/s,积分步长为τ=1.0×10−2s,考虑了桥梁的黏弹性特性.

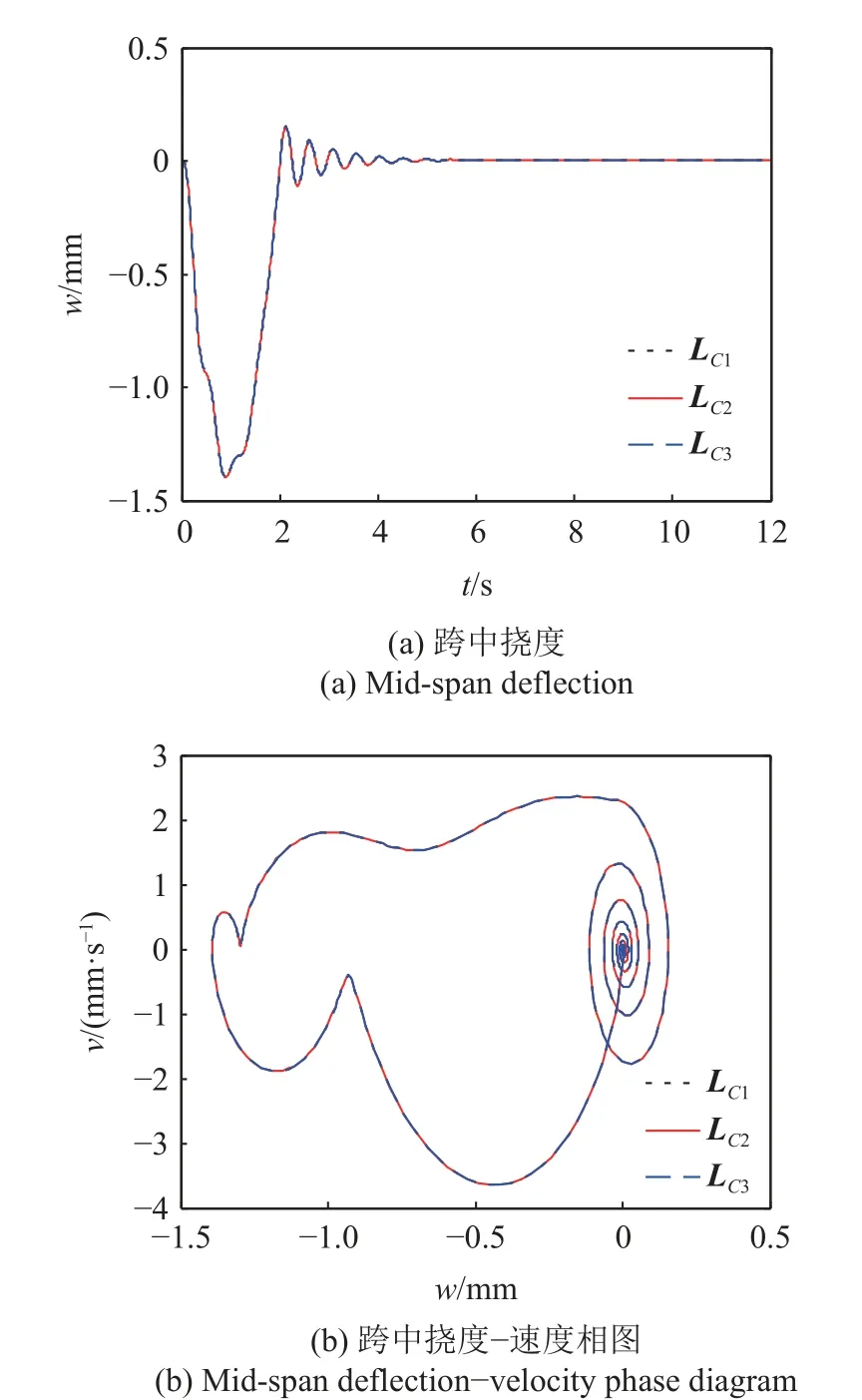
图12 τ=1.0×10−2 s,FPEI4-4 格式选取不同时变矩阵冻结方式的计算结果Fig.12 The numerical results calculated by FPEI4-4 scheme under different parameter freezing forms with time step τ=1.0×10−2 s

从图12 中可以看出,由于考虑了桥梁的黏弹性,在汽车下桥以后,跨中位移振动迅速衰减为0,在相图中曲线逐渐趋于(0,0)点,这和实际情况相符.由于此时零解为渐近稳定的,奇点(0,0)为稳定焦点,如图12(b)中右侧所示,相图中的轨线表现为盘旋趋近原点(0,0),图12(b)左侧为车桥耦合初始阶段的轨线.同时从图中可以看出,应用本文构造的显式FPEI4-4 格式进行数值积分计算时,选取3 种不同参数冻结方式时的图线几乎吻合,均具有良好的数值计算效果.虽然在对时变矩阵L(t)进行参数冻结时引入了误差,但数值结果显示,即使选择了较大的步长,依然可以得到较为满意的结果,这体现了本文所提出算法在计算车桥耦合振动问题时的优势.

进一步分析了采用不同参数冻结形式时的计算结果和积分步长 τ=1.0×10−4s时SRK2-4 格式计算参照解的误差,结果如图13 所示.从图13 中可以看出,采用LC2和LC3参数冻结形式时产生的误差峰值相近,而采用LC1的时变参数冻结方式产生的误差要明显小于LC2和LC3,具有更好的数值计算效果.表4进一步给出了FPEI4-4 格式选取不同积分时间步长时,不同参数冻结形式与参照解的最大误差.从表4中同样可以看出,选取LC1的时变参数冻结方式具有更好的数值精度,而选用LC2和LC3参数冻结形式时精度稍差且峰值误差接近,而此车速下跨中挠度的最大值为 1.395 9×10−3m,不同冻结方式的跨中计算结果均是可接受的.基于平均化的思想,在处理不同的车桥耦合动力学问题时,建议采用LC1的时变参数冻结方式.

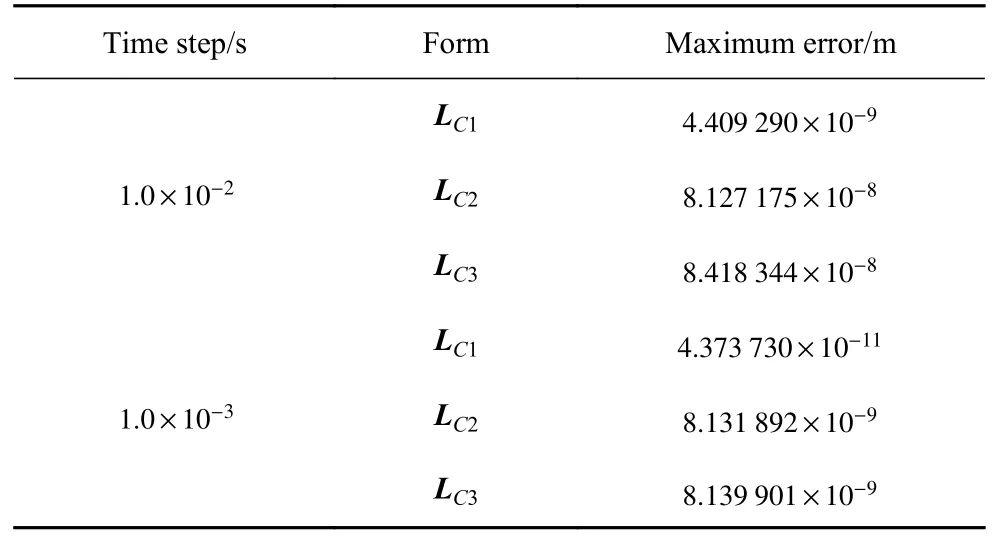
表4 不同冰冻近似方式的对比Table 4 Comparison of different parameter freezing forms

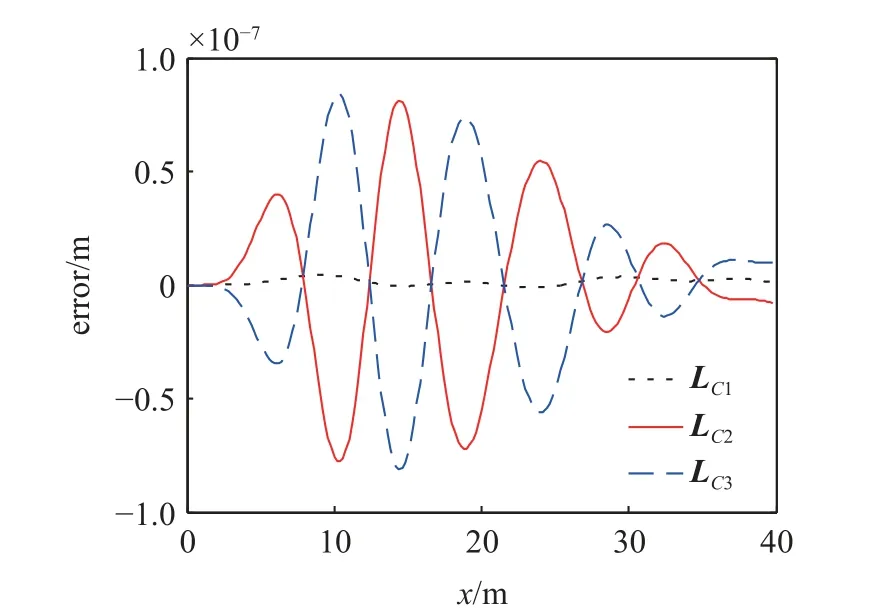
图13 τ=1.0×10−2 s,FPEI4-4 格式不同时变矩阵冻结方式求解跨中挠度的计算误差Fig.13 The numerical errors of mid-span deflection calculated by FPEI4-4 scheme under different parameter freezing forms with time step τ=1.0×10−2 s

4 结论

本文基于车桥耦合振动系统中时变、非线性动力学方程组的求解问题,提出了一种新的数值计算方法,即时间参数冻结的精细指数积分方法.基于简单的四级四阶显式Runge-Kutta 格式(RK4-4)构造了相应的时间参数冻结精细指数积分格式(FPEI4-4 格式).以考虑了桥面铺装层、桥梁结构几何非线性和黏弹性特性的车桥耦合问题为例,推导了描述该问题的时变、非线性动力学方程组,应用本文提出的FPEI4-4 格式进行了求解.首先,通过与实验测试结果进行对比,体现了本文理论建模和数值计算的有效性和实用价值.进一步,通过与近似解析解、二级4 阶隐式辛Runge-Kutta 格式(SRK2-4)计算的参照解以及经典的Newmark-β数值积分格式计算结果进行对比,体现了本文所提算法的良好数值特性.文中主要结论如下:

(1) 所提出的时间参数冻结精细指数积分方法可方便处理时变、非线性动力学问题,即使选取较大的积分步长也能得到满意的结果,有效地提高了计算效率;

(2) 本文针对车桥耦合动力学问题提出的参数冻结精细指数积分法计算速度快,具有长时间的数值积分稳定性,能够有效地保持动力学问题的本质特性;

(3) 针对快时变问题,对时变系数矩阵参数冻结引起的误差会增大,但本文格式数值积分结果的误差仍可保持在较小量级,计算结果仍是可接受的;

(4) 在每一离散步,对于时变系数矩阵的参数冻结方式,建议选用上一积分时刻和本积分时刻矩阵的均值,但即使选择上一时刻矩阵值或当前时刻矩阵值进行近似,也能取得较满意的数值积分结果.

本文所提出的参数冻结精细指数积分法预期可为时变、非线性的车桥耦合动力学问题研究提供一种新的计算途径.