鳗鲡科鱼类变刚度特性对推进性能影响研究1)

张旭尧 崔 祚 尹存宏 程安楠

* (贵州大学机械工程学院,贵阳 550025)

† (贵州理工学院航空航天工程学院,贵阳 550003)

引言

在自然界中,大部分鱼类采用波动推进模式,通过神经信号激活鱼体两侧肌肉,利用鱼体的柔性波动特性及其与流体环境的相互作用,实现快速高效游动[1-2].鱼类在波动推进过程中可通过收缩/拉伸肌肉的方式调整身体刚度,以获得更高的推进速度和游动效率[3].例如,Luo 等[4]发现可通过调整仿生机器鱼的尾部刚度来提升推进性能.Shelton 等[5]发现柔性鱼体比刚性鱼体更容易实现快速游动.Tytell 等[6]和Wang 等[7]进一步发现同时调整驱动频率和鱼体刚度可更好地提升鱼类游动速度.太阳鱼生物实验发现当摆动频率相同时,低鱼体刚度会导致游动速度下降[8].虽然上述研究均表明鱼体刚度和驱动等参数对鱼类推进性能有着重要影响,但它们之间的交互影响机理分析还不深入.

波动推进鱼类由鱼体肌肉、脊椎、骨骼系统、肌腱和皮肤等弹性组织组成,通过肌肉收缩和伸长实时改变鱼体弯曲刚度,从而提升游动性能[9-10].从动力学角度看,鱼类在水中游动过程实质是鱼体内部动力学和外部流体环境相互作用的结果,其推进性能由鱼体主动弯曲和流体的反作用力共同决定[11-12].柔性鱼体可看作由弹性材料组成的变截面梁,杨氏模量可用来描述鱼体刚度.所以探究鱼体变刚度特性首先需要构建耦合鱼体内部动力学的游动模型,然后分析刚度特性对推进性能的影响.

在鱼类游动建模方面,鱼游模型可大致分为理论动力学模型和数值CFD 模型两类[13].鱼游理论动力学模型指利用经典流体力学理论,如Taylor 抗力理论、Lighthill 细长体理论和动作盘理论等,耦合鱼体动力学模型实现鱼游过程.而数值CFD 模型通常利用数值方法求解流体方程,并通过耦合求解鱼体动力学方程实现鱼游的模拟.例如,Tytell 等[13]建立了三维鳗鱼游模型,研究表明鱼体刚度直接影响鳗鱼游动速度和启动加速度,并预测鱼体大刚度更容易得到更大的游动速度,但会降低启动加速度.Wei等[14]在CFD 鱼游模型基础上,利用效率优化方法发现鲹科鱼类在高斯特劳哈尔数和低雷诺数下容易实现高效率游动.

目前,鱼类游动模型大多采用鱼体波曲线(如文献[14])或鱼体内部激活波为驱动,缺少肌肉驱动模型的深入分析.McMillen 等[15-16]结合生物学实验,构建了基于钙离子模型的肌肉力非线性驱动模型,并结合Taylor 抗力理论建立了鱼游模型,研究了鳗鲡科鱼类激活波和弯曲波的滞后现象.后续沈昊嫣等[17]、Williams 等[18]、Blight[19]和Long 等[20]研究进一步发现鱼体弯曲曲率、肌肉激活波等与鱼体刚度调整有关.但是目前缺少鱼体肌肉驱动、鱼体刚度变化和游动性能的耦合关系的深入研究,也没有讨论鱼体驱动力幅值的影响.

鉴于上述分析,本文以鳗鲡科鱼类(如七鳃鳗、盲鳗和鳗鱼等)为研究对象,利用钙离子肌肉力驱动模型,基于黏弹性梁动力学模型建立了鱼游模型,采用数值模拟方法分析鱼体驱动条件、刚度特性与游动性能的耦合关系.

1 鱼类游动动力学建模

1.1 鱼体动力学方程

鳗鲡科鱼类在游动过程中,肌肉激活行波沿鱼体头部向尾部逐渐传递,激活鱼体两侧肌肉产生肌肉收缩或伸长的驱动力,从而使得鱼体弯曲变形.将鱼体看作水中受到流体力作用的黏弹性梁,鱼体波动推进过程受到内部弯矩和流体动力的相互作用.

如图1,鳗鲡科鱼类在水中的游动可以简化为一个平面问题,将鱼体的摆动平面设为投影平面,并在惯性参考系下建立鱼体的直角坐标(x,y),以弧长s和转动角φ建立鱼体曲线坐标.一般鳗鲡科的鱼体横截面近似为椭圆形,鱼体的高度和宽度沿体长逐渐减小.根据鳗鲡科鱼类的体态特征,设定模型长度L=21 cm,鱼头长为0.1L,鱼身长为0.6L,鱼尾长度为0.3L;鱼体横截面为椭圆,其高度方向为长轴,宽度方向为短轴,则短半轴a(s)和长半轴b(s)沿着鱼体长度的分布可描述为

图1 基于黏弹性变截面梁的鱼游模型Fig.1 The dynamic model of fish body based on the viscoelastic rod with variable cross-sections

为确保鱼体弯曲变形过程中长度不发生变化,引入不可伸长条件,描述为

式中,弧长s表示鱼体全长,转动角φ表示鱼体中线上任意一点的切线与x轴夹角.

如图1,黏弹性杆上任意一处节段都会受到接触力F=(f,g)、弯矩M、流体力W=(Wx,Wy)的作用,其中接触力和弯矩是施加在鱼体上任意节段区域内的力,而流体力来自与外部流体环境的相互作用,平衡线动量方程和角动量方程后,建立鱼体运动学和弯曲变形方程,描述为

式中,ρ为鱼体密度;A为鱼体截面积,A=πab;I为椭圆截面惯性矩,I=πab3/4;Wx和Wy分别为沿x轴和y轴方向的流体力,f和g分别代表沿x轴和y轴方向的接触力,M为鱼体弯矩大小.

柔性鱼体与周围流场的相互作用力W可利用Taylor 抗力理论进行分析,描述为

其中,流体力W的法向n和切向t的分量分别为

式中,ρf为流体密度,μ为流体黏性系数;Cn为法向系数,设置为Cn=1;vn和vt分别为法向速度和切向速度.

方程(5)中的弯矩M包含弹性应力、黏性应力产生的力矩和肌肉激活波,描述为

式中,EI为弯曲刚度;δ为黏性阻尼;K为鱼体肌肉激活行波函数.

1.2 鱼游动力学模型离散化

根据1.1 节的设定,现将鱼体摆动平面设为投影平面,并建立鱼体的直角坐标(x,y).如图2,将鳗鲡科鱼体离散成冗余串并联结构,各串并联结构单元距离为h,并由铰链连接.多刚体串联结构代表鱼体脊椎以描述鱼体的波动运动情况.并联在鱼体两侧的线性弹簧、阻尼器、驱动器代表鱼体肌肉驱动及鱼体黏弹性动力学特性,用以分析鱼体变刚度特性.

图2 鳗鲡科鱼体离散化模型Fig.2 The discretization model of anguilliform fish

在惯性坐标系(x,y) 下,离散不可伸长条件方程(2),如下

在惯性坐标系(x,y) 下,离散鱼体运动学方程式(3)～式(4)和弯曲变形方程(5),如下

式中,Ji为鱼体离散体的转动惯量,Ji=ρIih;mi为离散体质量,mi=ρAih.

在惯性坐标系(x,y)下,离散鱼体弯矩方程(8),如下

进一步,根据图2 的离散鱼体几何尺寸关系,离散的弯矩方程(14)便改写为如下形式

式中,FRi和FLi分别为右、左侧的阻尼力、弹簧力和驱动力的合力;LRi和LLi分别为鱼体左、右侧到旋转中心的力臂;Ki为鱼体肌肉激活行波函数,1.3 节中有详细介绍;γ为阻尼器的阻尼,γ=aiμ/2;λ为线性弹簧的刚度,λ=aibiε;Hi为第i节鱼体的截面宽度,为了近似于肌肉的均匀分布设置Hi=bi/2;其中μ为阻尼系数,ε为弹性系数,ai为第i节鱼体的短半轴长度,bi为第i节鱼体的长半轴长度.上述相关参数和式(15)的具体含义和推导详细内容参见文献[15].结合方程(14)可知在方程(15)中,等式右边第3 项为弯曲刚度项,即EIi=2aiε/4.在图1 的椭圆截面鱼体中,若将Ii=πai/4 带入弯曲刚度项,则弹性系数变为ε=Eπ/2,其中E为杨氏模量,则鱼体弯曲刚度Gi可变为如下形式

式中,通过改变杨氏模量E便可统一变化鱼体的弯曲刚度,且鱼体的弯曲刚度与横截面积、杨氏模量呈正比关系,这一设置符合生物学[16,21],因为肌肉收缩会在横截面上产生应变[22],进而引起横截面的变化,并且越大的弯曲曲率会带来越大的应变,而应变对推进性能的主要影响在于变化了鱼体的身体刚度,即越大的应变会带来越大的身体刚度[23].

1.3 鱼体肌肉力驱动模型

本文的肌肉力生成采用Williams 等[15]的钙离子肌肉力模型,其包括线性化的Hill 肌肉模型和钙动力学模型两部分组成.

在线性化的Hill 肌肉模型中,一束肌肉纤维被视作一组串联组成的收缩元件和弹性元件.从头至尾传播的运动神经元激活行波促使肌肉收缩.当肌肉未被激活时,收缩和弹性元件不运动,它们两者产生力的大小相等.当肌肉被激活时,收缩元件缩短带动弹性元件伸长.在整个肌肉激活过程中,收缩和弹性元件产生力的大小相等,且收缩量等于伸长量.

设置弹性元件产生力P与其伸长量成线性关系,其对应图2 中的线性弹簧,表达式为

式中,μs为肌肉纤维弹性系数;ls为肌肉纤维变形后长度,即弹性元件伸长后的长度;ls0为肌肉纤维初始长度,即弹性元件的初始长度.

设置收缩元件产生力Pc随时间的变化呈倒钟形非线性关系,其影响因素有收缩长度、收缩速度和钙离子结合过程,表达式为

式中,P0为实验测得最佳肌肉力[13],60.86 mN/mm2;lc为肌肉收缩元件长度,vc为肌肉收缩速度,λ(lc)和α(vc)是生物学拟合常数;RCaf为肌肉细丝上钙离子结合位数量和细丝结合位数量的比值,由钙动力学模型给出.上述参数的具体含义和钙动力学模型详细内容参见文献[15].

本文钙动力学模型均采用生物学试验数据,由于实验数据肌肉激活频率不高于2 Hz,所以本文研究肌肉激活频率均不大于2 Hz.此外,肌肉收缩过程所需的时间,由下式描述

式中,kt为时间常数,100 s−1;P外弹性元件产生的力,其对应图2 中的线性弹簧(左侧为PLi,右侧为PRi),即肌肉驱动力;Pc为收缩元件产生的力.

联立方程式(17)～式(19)和钙动力学模型便可求解出肌肉驱动力P.结合本文的冗余串并联鱼体结构和肌肉力驱动模型,将式(15)中的鱼体激活驱动函数Ki定义为如下形式

式中,bi为第i节椭圆截面长半轴尺寸;D为肌肉驱动幅值系数,被用来缩放肌肉驱动力;PLi和PRi为第i个结构单元左、右两侧的肌肉驱动力.值得注意的是,激活驱动函数受左、右侧肌肉驱动力PRi和PLi的差异影响,使得运动控制存在冗余性,具体表现是降低了肌肉的驱动激活,从而减少弯曲刚度,事实上这是符合生物学中的肌肉收缩,因为当左右侧的肌肉被同时激活时,肌肉会产生分布式的轴向压缩载荷[1],引用经典的欧拉屈曲(Euler buckling)问题可以解释为外部施加的轴向载荷取消了弯曲刚度.

本文的鳗鲡科鱼游模型涉及了多个方程,为明晰求解流程,在图3 中给出了鳗鲡科鱼游模型的求解流程图.

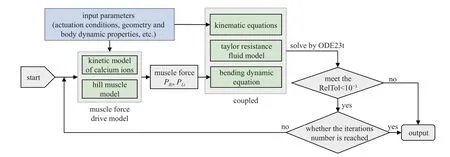
图3 鳗鲡科鱼游模型求解流程图Fig.3 The solution flowchart of anguilliform fish model

2 鱼游模型验证

文献[1]和文献[24]均采用与本文相同的离散化方法,文献[1]中设置链节数为10,验证了结果的收敛,只是游动速度下降了40%,文献[24]中设置链节数为21,得到了更贴近鳗鲡科生物动力学行为的结果,所以本文设定的离散节数N=21.

本文采用等距生物实验拟合肌肉驱动力数据[15],设定肌肉激活行波的波速为1 BL/s (体长/秒).基于生物学实验数据[25],确定鳗鲡科鱼类,肌肉激活位置神经信号持续时间为0.36 s,肌肉激活频率为1 Hz.本文模拟结果,若无其他特殊说明,模型输入参数默认均采用表1 数据.

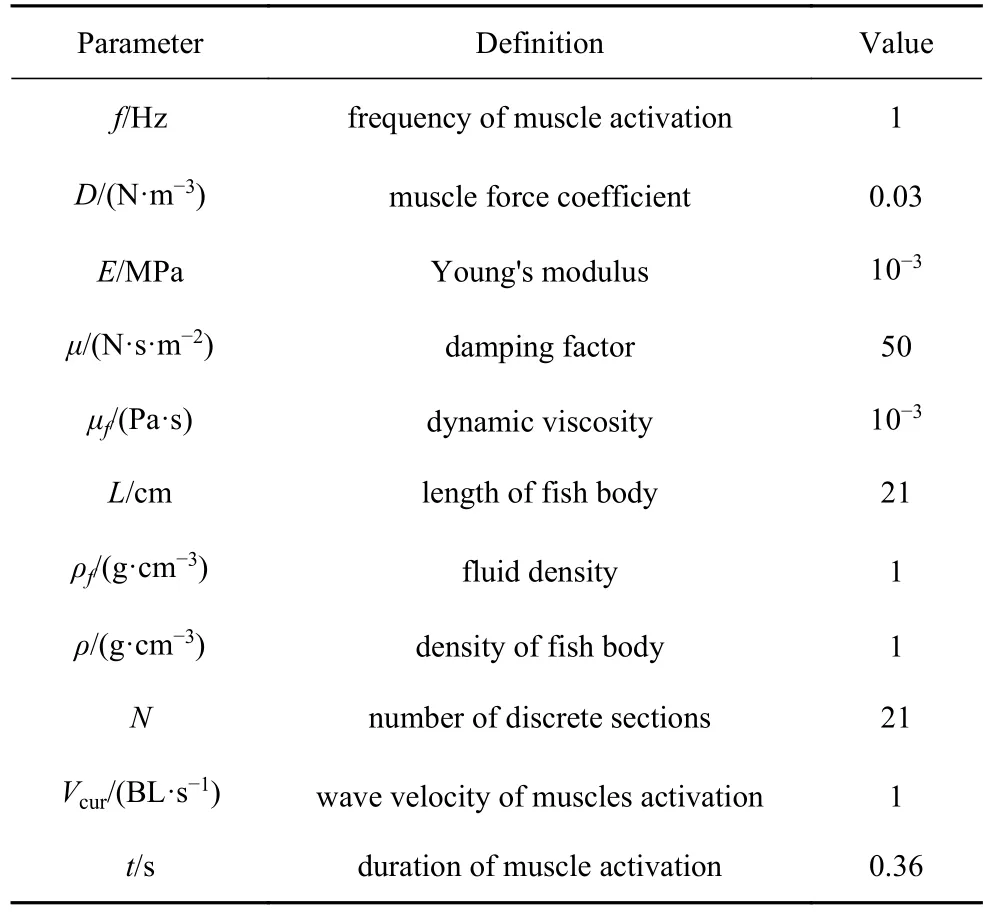
表1 鳗鲡科鱼体模型参数Table 1 The parameters of anguilliform fish model

如图4,在无量纲化的肌肉驱动力结果中,从肌肉激活开始,肌肉驱动力在0.36 个周期时发展到最高,随后的0.64 个周期逐渐减少,体现了鱼体肌肉从激活到生成驱动力的过程.依据文献[24]中生物学实验数据,肌肉驱动幅值确定的范围为0.05 ±0.02 N/m3,不妨设定本文的默认肌肉驱动幅值系数为0.03 N/m3,实际上该数值会随鱼体的游动状态而发生改变,详细讨论见3.1.该过程与McMillen 等[15]和Williams 等[16]的生物学肌肉力数据相匹配,表明本模型使用的肌肉力模型符合生物学驱动过程.

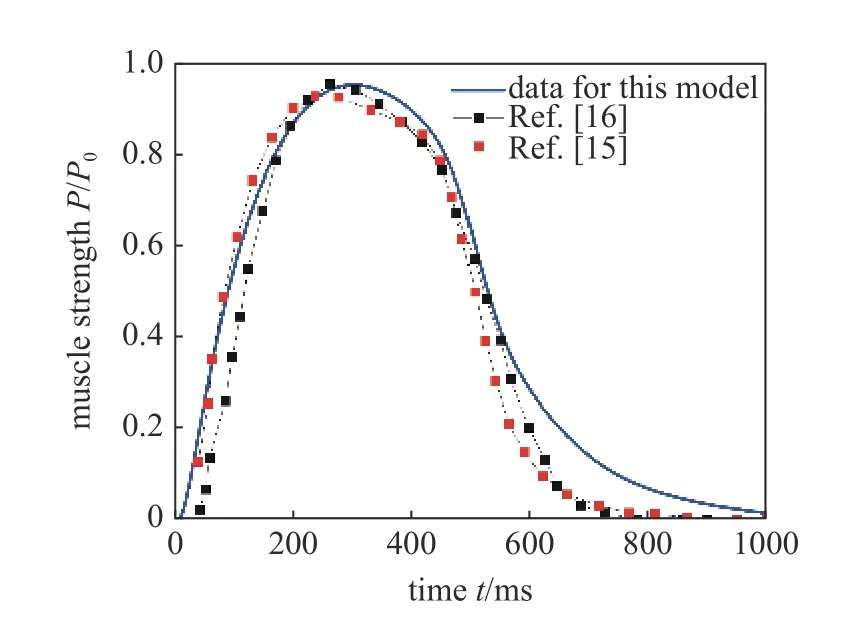
图4 基于钙离子肌肉力模型产生的驱动力Fig.4 The driving force generated based on the kinetic model of calcium ions

如图5,游动速度结果中黑线表示游动速度曲线,红线表示拟合后的鱼体平均渐进游动速度曲线.蓝线为相同输入参数下,McMillen 等[15]模拟的鱼类最大平均渐进游动速度0.40 BL/s,与本文计算结果0.39 BL/s 非常接近.

图5 游动速度结果Fig.5 Results of swimming speeds

如图6,鱼体波结果在头部和尾部有明显上翘,并且包络线沿着身体逐渐变高,这些都符合鳗鲡科鱼体波的生物学观察.与McMillen 等[15]在相同的模型输入参数下的模拟结果相比,无论是包络线发展趋势,还是头部和尾部的上翘,都有着相近的结果.

图6 鱼体波结果Fig.6 Results of fish midline motions

如图7,是模拟得到的激活波和弯曲波结果,其中激活波的波速为1 BL/s,模拟得到的波速比(弯曲波波速/激活波波速)为0.782,在相同的模型输入参数配置下,与McMillen 等[15]模拟的波速比结果0.780相近,并且弯曲波随时间的发展相同.

图7 波速比结果Fig.7 Results of wave speed ratios

3 游动性能影响因素分析

3.1 驱动力系数的影响

当驱动幅值系数从10−2N/m3变化到1 N/m3时,鱼体肌肉驱动系数对游动速度的影响如图8 所示.当肌肉激活频率为1 Hz 时,游动速度会随着肌肉幅值系数增大而先增大后减小;但随着肌肉激活频率不断增大(如2 Hz),游动速度会随着肌肉幅值系数增大而增大并逐渐趋于稳定.在不同肌肉激活频率下,鱼体获得最大游动速度的肌肉驱动幅值也逐渐增大,如表2 所示.

表2 不同驱动幅值对应最优速度表Table 2 Table of the optimal speeds varied with different driving amplitudes

图8 不同频率下肌肉驱动幅值系数对游动速度的影响Fig.8 The effects of muscle force coefficient on swimming speed at different frequencies

由图8 和表2 可知,鳗鲡科鱼类可通过肌肉驱动幅值来匹配合适的摆动频率,较大鱼体肌肉力驱动对应较大的摆动频率.由于杨氏模量间接变化了鱼体刚度,可进一步预测,在鱼体刚度固定情况下,鱼类极可能通过实时调整肌肉力驱动幅值来匹配最佳游动速度,满足其最佳的游动效率.上述结论与Williams 等[24]研究结论相同,这也间接验证了本文所建鱼游模型的正确性.

3.2 鱼体刚度与驱动力关系的分析

生物学研究发现,七鳃鳗鱼体的杨氏模量为47～99 kPa[8];鳗鱼的杨氏模量约为0.1 MPa[15];盲鳗的杨氏模值约为0.24 MPa[26].由于鳗鲡科鱼类的杨氏模量实验数据有限,本文为研究鱼体刚度变化对游动性能的影响,所以有目的适当扩大鱼体杨氏模量的变化范围,设其变化范围为1 kPa～1 MPa 之间.

游动鱼类游动的速度计算采用文献[1]中的计算方法,即单位时间内游动位移的变化率,单位有两种,一个是BL/s (体长/秒),一个是cm/s.如图9,当肌肉驱动力幅值D等于0.01 N/m3时,游动速度呈先增大后降低的变化趋势,存在最优游动速度;当D＞0.03 N/m3时,鱼体游动速度随杨氏模量的增大缓慢上升并逐渐趋于稳定.值得注意的是,当D=0.03 N/m3时,鱼体在不同杨氏模量条件下均可获得最佳游动速度.

图9 不同驱动幅值下鱼体刚度对游动速度的影响Fig.9 The effects of Young’s modulus of fish body on swimming speed under different driving amplitudes

游动鱼类的加速度计算,采用文献[13]中的计算方法,即鱼体在一个尾部节拍周期内游动速度的变化率.如图10,当D=0.03 N/m3时,启动加速度会随杨氏模量的增大而先增大后降低,且高于其他驱动幅值.当D＞ 0.03 N/m3时,启动加速度随杨氏模量增大而缓慢增大并趋于稳定.当D=0.01 N/m3时,启动加速度总体数值偏小.

图10 不同驱动幅值下鱼体刚度对启动加速度的影响Fig.10 The effects of Young’s modulus of fish body on the start acceleration under different driving amplitudes

综合上述研究表明,鱼类可通过肌肉产生合适的驱动幅值,以获得最大游动速度或最大启动加速度,且过大或过小的肌肉驱动幅值系数都会降低游动速度和启动加速度.在本文算例中,获得最大游动速度和启动加速度的鱼体最佳驱动幅值系数为0.03 N/m3.在Tytell 等[13]研究中,发现当鱼体刚度增大时,游动速度和启动加速度都呈现先增大后减小的变化趋势,该结论与本文D=0.03 N/m3的变化趋势相一致.但D＞ 0.03 N/m3时,游动速度或启动加速度并不会随鱼体刚度增加而先增大后下降,这也说明鱼类肌肉在过驱动状态下,虽然游动速度和加速度还可以维持较高水平,但肌肉消耗功率较大,鱼类将不在优先选择该状态进行波动推进.综合上述讨论,本文后续肌肉驱动幅值系数选择0.03 N/m3开展研究.

3.3 鱼体刚度对游动速度的影响研究

如图11,对于不同肌肉激活频率,鱼类游动速度随杨氏模量的增大而增大,而后当E＞ 0.01 MPa 时,游动速度随杨氏模量的增大而缓慢减小.如表3 所示,结果表明存在最优杨氏模量,使得鱼类在确定驱动条件下获得最快游动速度.

表3 不同肌肉驱动频率和杨氏模量条件下的鱼体最优速度Table 3 The optimal velocity of fish body under different muscle drive frequencies and Young's modulus

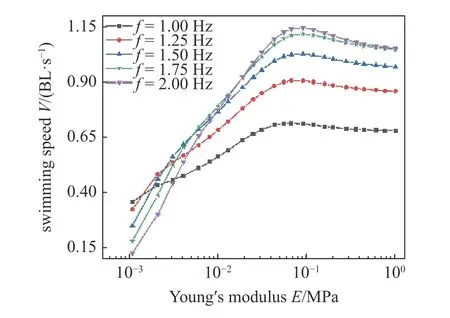
图11 不同肌肉驱动频率下鱼体刚度对游动速度的影响Fig.11 The effects of fish body stiffness on swimming speed under different muscle driving frequencies

当杨氏模量在0.08 MPa 附近时,肌肉激活频率越大对应的游动速度也越大,这是因为高激活频率会造成肌肉在收缩过程还未结束便被再次激活拉长,使得整个鱼体肌肉激活过程不完整,使鱼体摆动幅值变小,游动速度降低,这与文献[18]研究结论相一致.

如图12,对比固定刚度(E=0.001 MPa)和变刚度(E=0.1 MPa)条件下的鱼体游动速度结果,发现鱼类可通过改变刚度,有效提升鱼类的游动速度.以2 Hz 肌肉激活频率为例,通过改变刚度,游动速度由0.72 BL/s 增加到1.12 BL/s,提升了0.55 倍.该结论充分体现了鱼类变刚度特性对游动性能的重要影响,也为后续变刚度仿生机器鱼设计提供理论依据.

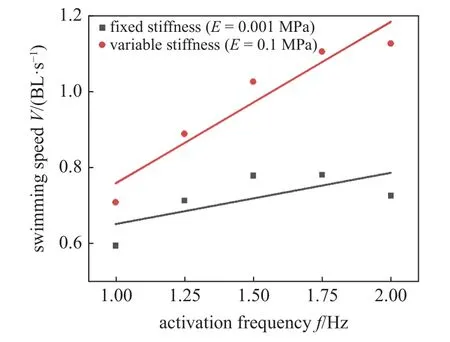
图12 鱼体变刚度特性对游动速度的影响Fig.12 The effects of the variable stiffness of fish body on the swimming speed

3.4 鱼体刚度对加速度的影响研究

本文还研究了鳗鲡科鱼类在不同肌肉激活频率下,鱼体杨氏模量对启动加速度的影响.如图13 所示,对于不同激活频率,启动加速度随杨氏模量的增大而迅速增大,当E＞ 0.1 MPa 时,加速度会出现缓慢下降趋势.当杨氏模量在0.1 MPa 左右时,各肌肉激活频率都有一个最大启动加速度,如表4 所示.

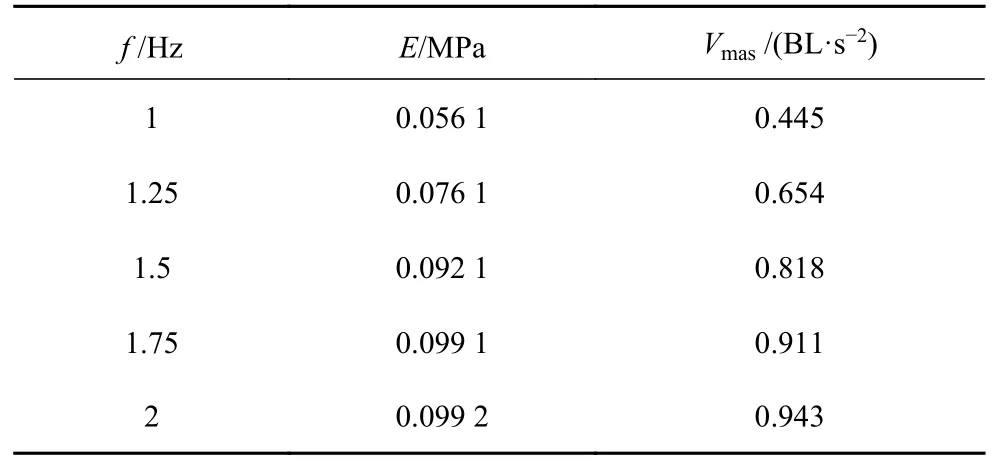
表4 不同肌肉驱动频率和杨氏模量条件下的鱼体最优启动加速度Table 4 The optimal start acceleration of fish body under different muscle drive frequencies and Young's modulus

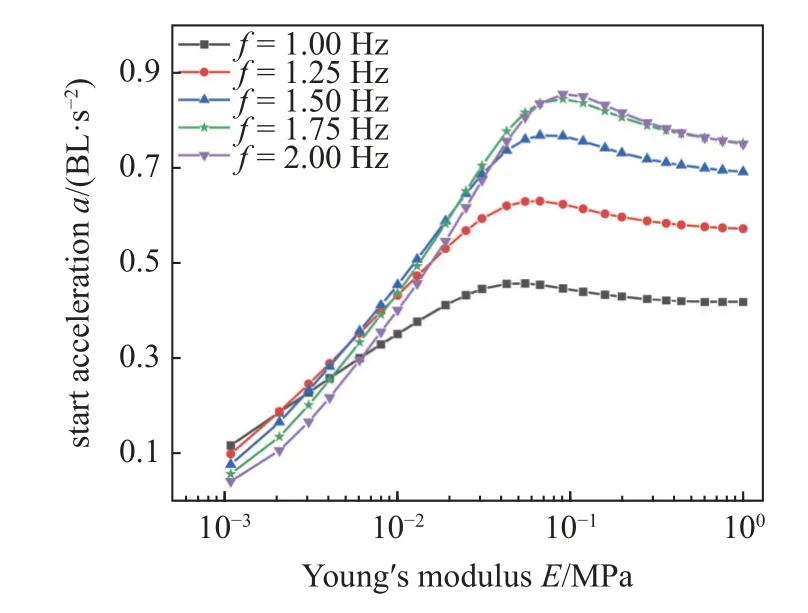
图13 不同肌肉驱动频率下鱼体刚度对加速度的影响Fig.13 The effects of fish body stiffness on the start acceleration under different muscle driving frequencies

对比表3 和表4,发现在不同肌肉激活频率下,获得最大游动速度的杨氏模量普遍大于获得最大启动加速度的杨氏模量.该结果表明不同肌肉激活频率下,鱼体通过增大刚度来获得更快游动速度,减小刚度得到更快启动加速度,该结论与Tytell 等[13]的预测相符.

图14 中展示了鱼体变刚度对加速度的影响.图中黑色曲线是杨氏模量在0.01 MPa 时加速度拟合曲线,红色曲线是各个频率下最优杨氏模量条件下加速度的曲线拟合,其中所采用的拟合方法是Akima插值拟合算法.表明可通过提升鱼体刚度方式来更快达到稳态速度.总体上,随着肌肉激活频率的增加,加速度的增幅也越大.鱼体变刚度特性对启动加速度有着显著影响,以2 Hz 激活频率为例,变刚度鱼体加速度从0.41 BL/s2到0.94 BL/s2提升了1.29 倍.

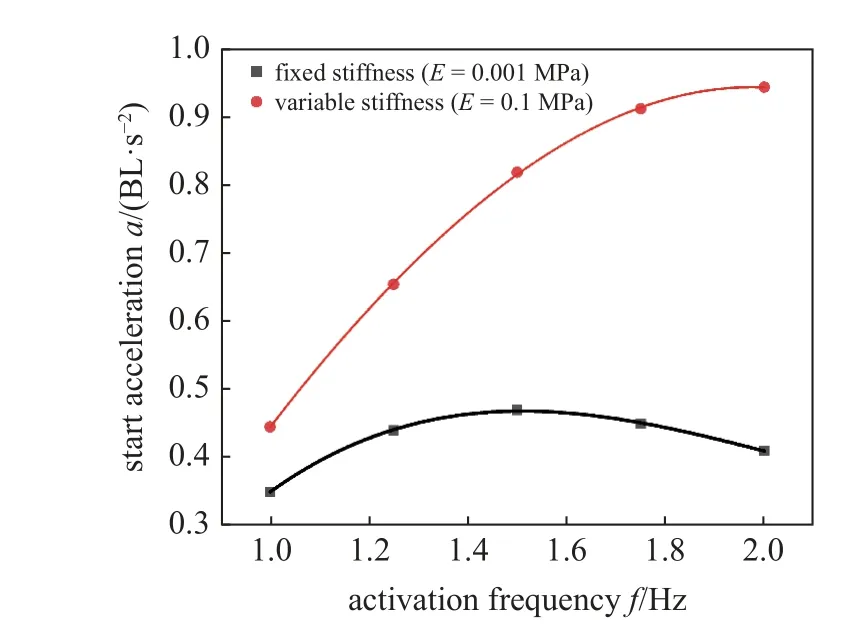
图14 鱼体变刚度特性对启动加速度的影响Fig.14 The effects of the variable stiffness of fish body on the start acceleration

文中拟合以及参数分析得到的分数阶次范围都超过1,这与驱动方式有关,因为同是作鳗鲡科游动分析,文献[24]中采用肌肉力驱动,得到了类似的结果,而文献[1]中提前设置的正弦曲率驱动并没有出现类似的情况.

4 变刚度特性实验验证

本章为了验证本文仿真得出的变刚度特性结论,忽略阻尼影响,设计了变刚度实验平台.如图15(a)和图15(b),整个机器鱼由弹性的硅胶包裹,因为鳗鲡科类仿生机器鱼的设计困难,所以设计了固定在机架上由5 个逐渐减小等距的(相距50 mm)鱼体关节总长为200 mm 以代表鱼身,并在平台连接处采用带轴承的铰链连接,以减小摩擦损失;连接在平台5 上的硅胶鱼尾长100 mm;舵机中心到平台1 的距离为33 mm 以代表鱼头.在整个实验过程中,固定在机架上的推力传感器将推力数据实时传至上位机.为了模拟鳗鲡科鱼类收缩两侧肌肉弯曲身体的过程,而采用舵机经拉绳驱动最后一节关节旋转带动鱼体弯曲的方式,并且连接关节的线性弹簧长度随着弯曲的变化而变化,从而模拟肌肉收缩过程.

图15 变刚度实验平台Fig.15 The experimental platform of variable stiffness

如图15(c),实验所设计的各关节鱼体在实际摆动弯曲时,因为各个关节间的角度变化并不大,最大值为10°位于尾部,且任意两平台间椭圆截面的短半轴和半长轴都只相差4 mm,所以当鱼体处在中性位(实验中相对转角q=0、支脚长度Lc=L1=L2,其中L1和L2为左、右两侧的弹簧支脚长度)时,在式(15)中采用如下设置,Hi=Hi+1,sin(ψi/2)=ψi/2,cos(ψi/2)=1,并结合图15(c)的三角关系可以推导出,当机构处于中性位时,转动刚度Q的计算方程如下

式中,k为实验弹簧刚度;ΔL为实验线性弹簧伸长量;rb为下平台宽度;Lh为实验链节长度.

由于本章实验为验证性实验,所以在选择实验弹簧刚度k时,遵循以下两点要求: (1) 鱼体处在中性位时,实验计算出的弹簧力k·ΔL范围要涵括模拟计算出的弹簧力λ·Δl范围,其中ΔL和k为实验弹簧的伸长量和刚度;Δl和λ为模拟弹簧的相对伸长量和刚度.当机构在中性位时,Δl=(lc−ls0)/ls0=1,ΔL=Lc−Ls0,其中ls0和lc为模拟弹簧初始长度和拉伸后长度;Ls0和Lc为实验弹簧初始长度和拉伸后长度.(2) 鱼体处在中性位时,模拟的鱼体弯曲刚度Gi和实验的鱼体转动刚度Qi分布规律应相同,其中弯曲刚度由式(16)求解,转动刚度由式(21)求解.当机构处于中性位时,各关节的具体尺寸如表5 所示.

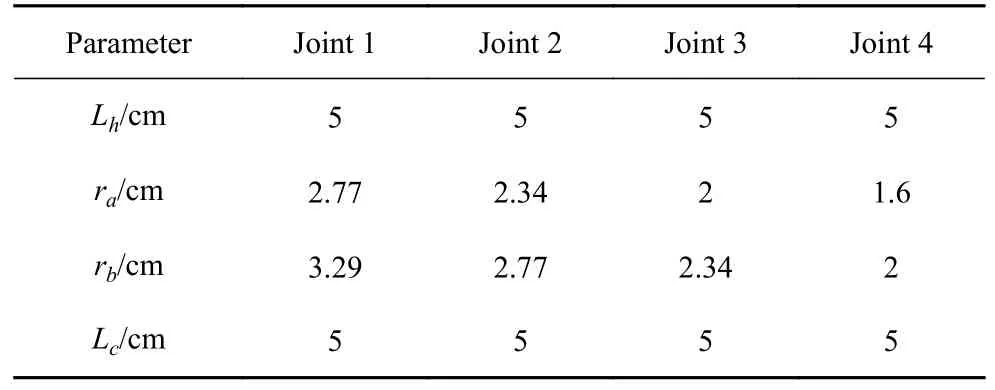
表5 鱼体关节尺寸参数Table 5 The joint parameters of fish body

因为图9～图14 中游动性能图都在E=0.1～0.05 MPa 范围内出现峰值,所以采用E=0.1 MPa和E=0.05 MPa 计算出的弹簧力作为模拟弹簧力的范围.按照1.1 的鱼体设定,鱼头、鱼身、鱼尾的长度比满足1: 6: 3,则在模拟的21 节鱼体中选用N=3,6,9,12 等距的4 个节段作为鱼身以满足比例要求,而实验设计的鱼身尺寸已满足比例要求.实验选择4 组长度为45 mm、外径为5 mm、不同线径(0.3 mm,0.4 mm,0.5 mm,0.6 mm)的挂钩弹簧,弹簧的刚度分别为k1=0.61 N/cm,k2=2.08 N/cm,k3=5.54 N/cm,k4=12.52 N/cm.采用上述设置,得到弹簧力和刚度计算结果,如表6～表9所示.表6～表7 模拟得到弹簧力的范围涵括了实验得到弹簧力的范围;表8～表9 模拟鱼体各节弯曲刚度和实验鱼体各节转动刚度的比例相同,即G3:G6:G9:G12=Q1:Q2:Q3:Q4.上述计算结果表明,本章所选用的4 组弹簧刚度k1,k2,k3,k4满足实验验证要求,实验选择了5 组不同的舵机驱动频率(1 Hz,1.25 Hz,1.5 Hz,1.75 Hz,2 Hz),推力实验数据如图16.

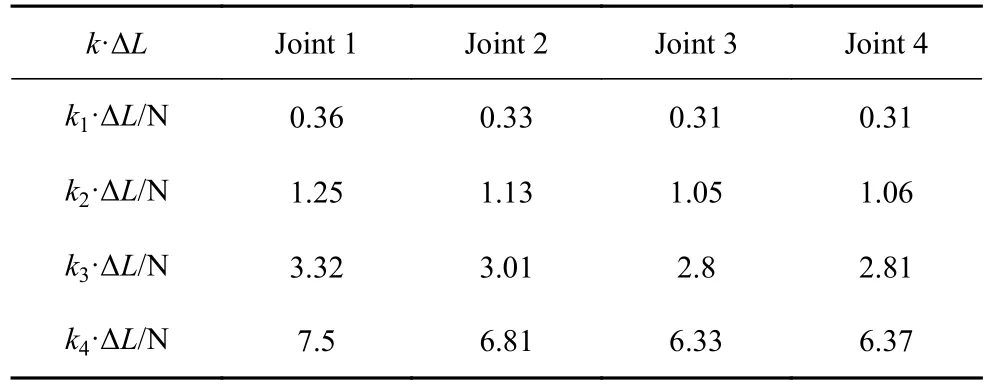
表6 实验中弹簧力k·ΔL 计算结果Table 6 Results of the spring force k·ΔL in the experiments

表7 模型中弹簧力λ·Δl 计算结果Table 7 Results of spring force λ·Δl in the simulations

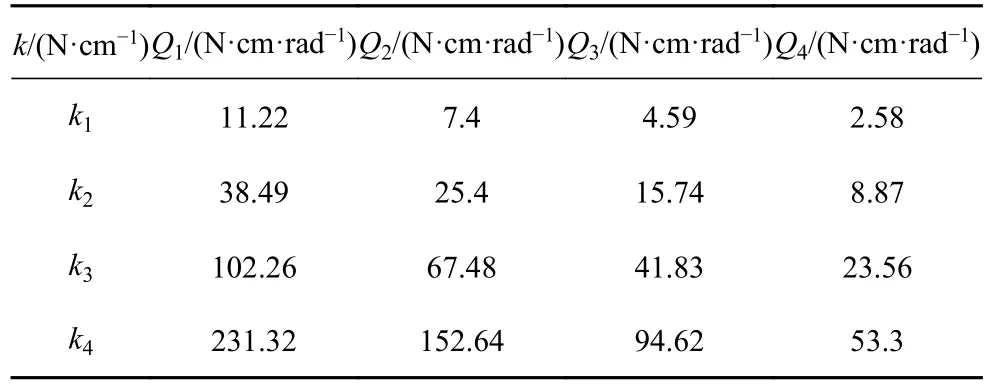
表8 实验中转动刚度Q 计算结果Table 8 Results of the rotational stiffness Q in the experiments

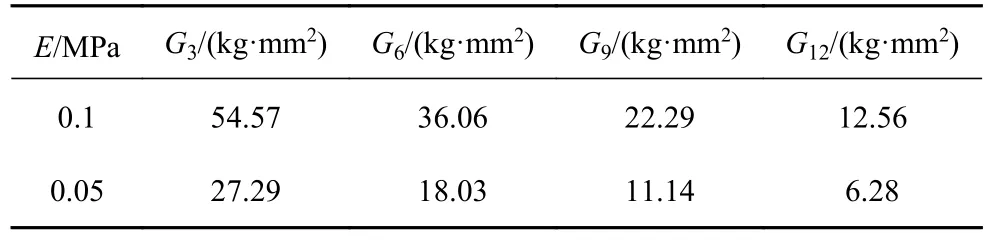
表9 模型中弯曲刚度G 计算结果Table 9 Results of the bending stiffness G in the simulations

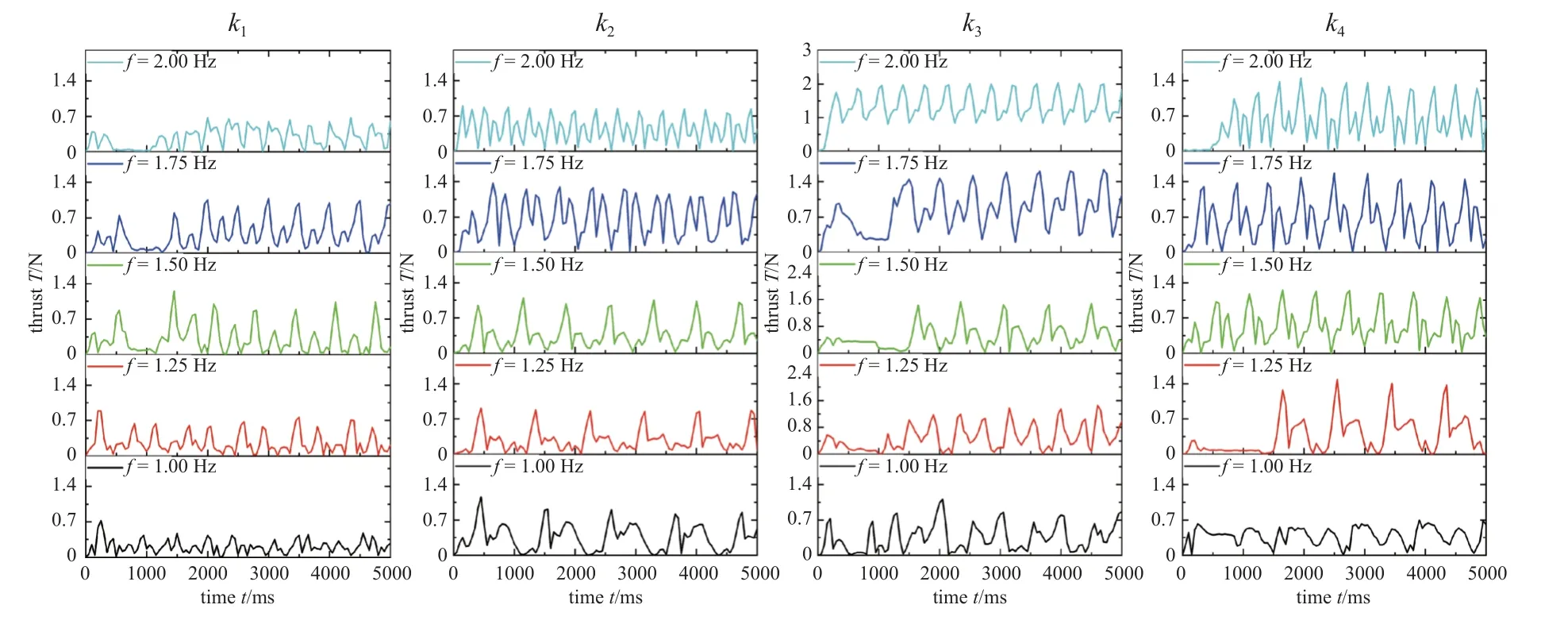
图16 实验测得的推力数据Fig.16 Thrust data measured in the experiments

图17 中的推力值是根据图16 的推力数据拟合出的最大平均值.图中随着弹簧刚度k的增加,推力曲线被随之抬升,当刚度达到k4时,推力曲线下移,在2 Hz 的驱动频率下,刚度为k4的推力为1.39 N,其推力相比于刚度为k1的推力值0.34 N 提升了3 倍.推力曲线随着频率的增加而不断爬升,特别是刚度等于k3时,推力由1 Hz 驱动频率下的0.39 N增加至2 Hz 驱动频率下的1.39 N,提升了2.5 倍,通过实验验证,鱼体的变刚度特性能显著提升鱼类推进性能.

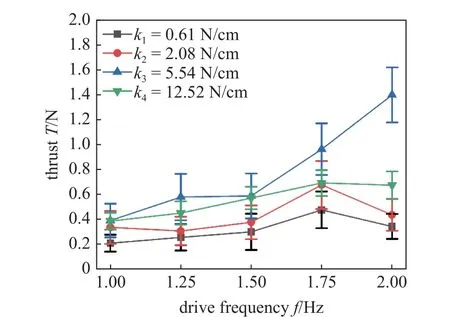
图17 变刚度条件下推力随驱动频率变化的实验结果Fig.17 Experiment results of the thrust varied with driving frequency under the condition of variable body stiffness

5 结论

本文基于串并联机构建立了鳗鲡科鱼类游动模型,结合钙离子肌肉驱动模型,研究肌肉驱动力幅值、摆动频率和游动性能之间的影响关系,得到主要结论如下.

(1)针对鱼体肌肉驱动,鱼类通过增大肌肉驱动幅值来匹配更高驱动频率,以获得更快游动速度.当鱼体肌肉力驱动确定时,过高或过低驱动频率都会导致游动速度降低.

(2)当肌肉驱动力确定时,鱼类游动速度和启动加速度随弹性模量的增大而增大;当E＞ 0.01 MPa时,游动速度和启动加速度随弹性模量的增大而缓慢减小.

(3)鱼体变刚度特性能显著提升鱼类游动速度和启动加速度,结果表明在低频游动状态下(频率小于2 Hz),通过调整鱼体刚度大小,最大可提升0.55倍游动速度和1.29 倍启动加速度.该结论充分展现了鱼体变刚度对游动性能的重要影响.

(4)在不同激活频率下,鱼体获得最大游动速度的杨氏模量普遍大于获得最大启动加速度的杨氏模量.该结果表明鱼体可通过增大刚度获得更快游动速度,减小刚度得到更快启动加速度,该结论与Tytell 等在文献[13]中预测结果相符.