黏性牛顿流体液滴撞击干燥或预湿网面的实验研究1)

宗绍强 徐 龙,† 郝继光,2)

* (北京理工大学宇航学院,北京 100081)

† (西安交通大学航天航空学院,西安 710049)

引言

液滴撞击网面现象广泛存在于自然界和一系列工农业应用中,如喷涂[1-6]、防护衣物开发[7]、传热[8]、印刷[9-11]、两相分离[12-17]、口罩的开发与使用[18-21]和农药喷洒[3]等.液滴撞击网面经历复杂的动态过程,除了在网面上产生液滴撞击固体表面时的飞溅、铺展和反弹[22-33]现象外,还会在网面下产生穿透和破碎,形成二次液滴.液滴撞网结果通常分为以下3 种: 韦伯数较低时,撞击液滴在网面上扩散,不穿透网面,定义为不穿透;在韦伯数较高时,液滴撞击网面后在网面下方形成液指,液指不断裂并最终回缩到网面上表面,定义为不完全穿透;进一步提高韦伯数到大于某一临界值Wep,液指会破裂并在网面下产生二次液滴,这种现象被定义为完全穿透[34-38].

液滴撞击网面产生的二次液滴在有些场合是需要的,在另一些场合又会产生负面影响,因而工程中存在认清其规律和机理,从而实现调控的迫切需求.如,对于防护衣物开发和口罩的使用,二次液滴的出现会显著降低防护效果;而对于喷涂和印刷,二次液滴是有助于用更少液体实现更大覆盖面积的目标的.临界韦伯数Wep通常被用来界定从不完全穿透到完全穿透的转变,当撞击韦伯数大于Wep时,完全穿透现象出现,撞击会形成二次液滴;反之,撞击不会形成二次液滴[34].对于特定的液滴,也可用临界速度Up来界定两种现象的转变[35,38].

随着高速摄影技术的发展,直接观测液滴撞网现象变得可能,对该现象的研究在过去的20 年中引起了学者们的广泛关注.Lorenceau 等[38]对液滴撞击单孔进行研究,首次定义了Up,并提出了一个基于动压和毛细压力平衡的穿透预测模型,还根据实验结果拟合了模型中的系数.此后,类似模型被广泛应用于分析网面材料[37,39-43]、网面润湿性[35-36,43-48]、网面形态[49-52]、网面倾角[53]和网面预湿[19,34]等因素对临界韦伯数Wep或速度Up的影响,建立了适应这些特定因素的穿透预测模型[34-36,52].

前述研究都是基于低黏性液滴(大部分是水)撞击开展的,关注点仍是网面属性对撞击结果的影响.液滴属性[54-58]对撞击结果的影响最近也引起了学者们的注意,如Blackwell 等[54]、Mehrizi 等[55]研究了非牛顿流体液滴撞击网面的现象和规律;Wang 等[56]和Vontas 等[57]采用数值模拟方法研究了液滴黏性的影响;Abouelsoud 等[58]实验研究了不同黏性的低表面张力硅油滴撞击亲油网的现象和规律,预测了最大液指长度.然而,前述研究都没有关注网面预湿的影响,实际应用中的网面只要经过一次液滴撞击,就会被预湿[19,34];针对预湿的研究[19,34]虽有开展,但是都没有研究液滴黏性的影响,尤其是大表面张力液滴黏性的影响.

本文利用高速阴影成像技术,研究了大表面张力液滴(甘油水溶液)黏性、网面尺寸和网面预湿对液滴撞网结果的影响,获得了系列条件下的最大液指长度和形成完全穿透所需的临界参数,分析了关键因素的影响规律和机制,建立了考虑液滴黏性、网面尺寸和网面预湿的最大液指长度和形成完成穿透所需临界参数的预测模型,预测结果与实验结果吻合良好,为工程应用提供了实验依据和理论工具.

1 实验设置

实验装置如图1 所示.利用注射泵缓慢驱动注射器在毛细管口产生甘油水溶液液滴,液滴在重力作用下加速并撞击网面.实验中用到了10 种具有不同甘油质量浓度ψ的甘油水溶液,分别使用不同质量比的分析纯甘油和去离子水混合形成,其物理属性[59]如表1 所示.液滴由相同尺寸的毛细管生成,直径D是由图像处理获得液滴接触网面前的水平宽度Dx和垂直高度Dy,再由式(1)计算得出(D=2.5 ±0.15 mm).液滴撞击速度U是由图像处理获得液滴与网面接触前10 帧内液滴上下沿移动距离的平均值,再除以10 帧对应的飞行时间计算得出,速度通过升降平台改变针头到网面的距离X来调控(U=0.96～3.82 m/s)

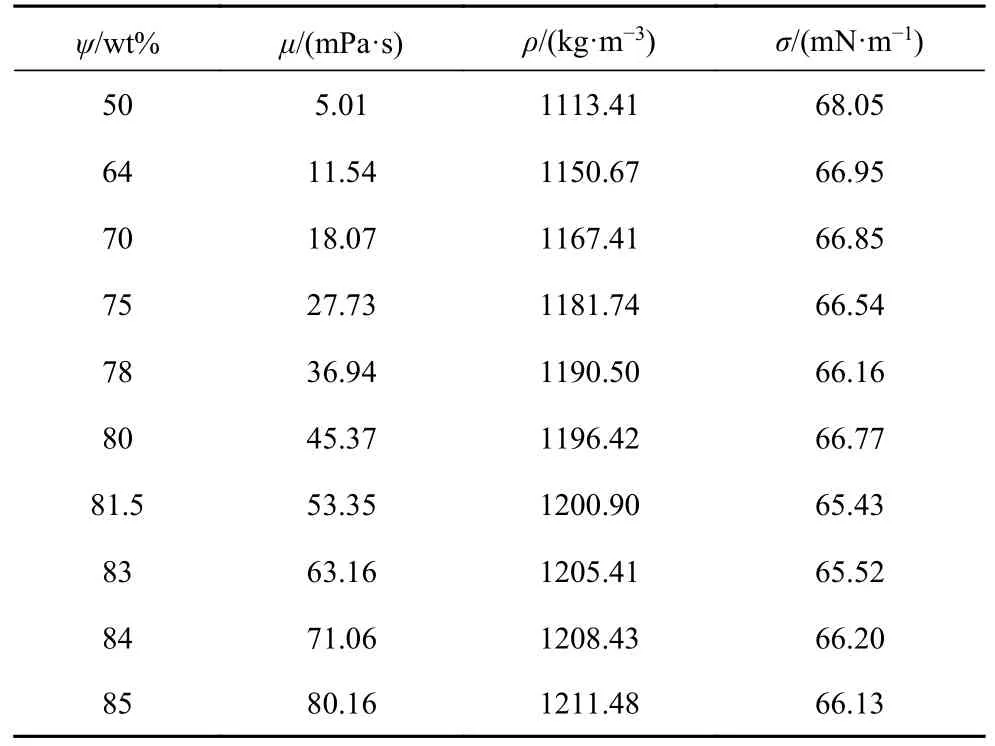
表1 甘油水液滴的物理属性(25 °C)Table 1 The physical properties of aqueous glycerol solutions at 25 °C

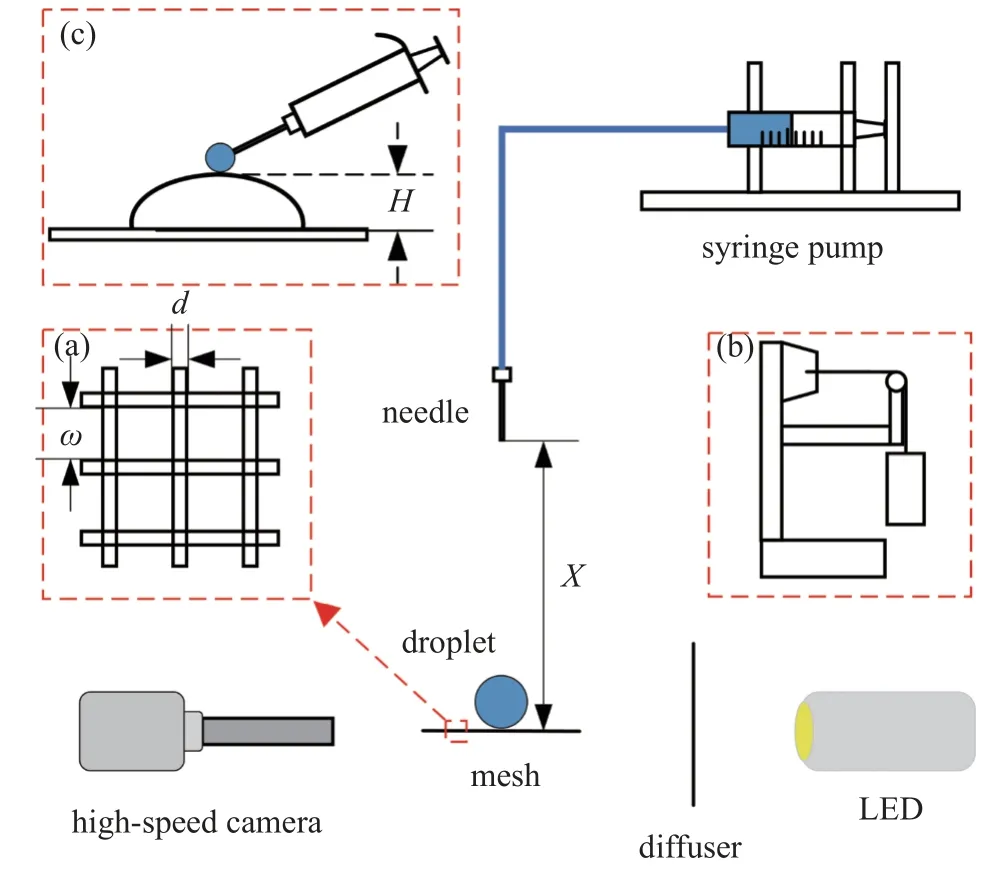
图1 实验装置示意图Fig.1 Schematic diagram of the experimental set up

本文用到以下无量纲参数: 雷诺数Re=ρUω/μ,韦伯数We=ρU2ω/σ,毛细数Ca=μU/σ.式中,ρ为液滴密度,U为液滴撞网速度,ω为网孔宽度(如图1(a)所示),μ为液体黏性系数,σ为液体表面张力系数,由Dataphysics OCA20接触角测量仪测定.

被碰撞网面为商用紫铜网,网面一端使用夹具固定,另一端利用砝码张紧网面(如图1(b)所示),使网面保持平整并减少液滴撞网过程中网面振动对液滴破碎的影响.实验中用到了5 种目数Nm的网面,它们的网孔宽度ω和网线直径d如表2 所示.为考量网面润湿性对实验结果的影响[60-63],我们使用ImageJ 软件测量了2 种甘油水液滴在5 种网面上的静态接触角θeq,如表3 所示,μ=5.01 mPa·s 和μ=80.16 mPa·s 液滴在网面上的静态接触角最大差值分别为10.3°和9.0°,该值相对各自的最小静态接触角均小于10%,因此网面润湿性的影响可以忽略.

表2 网面参数Table 2 The mesh parameters

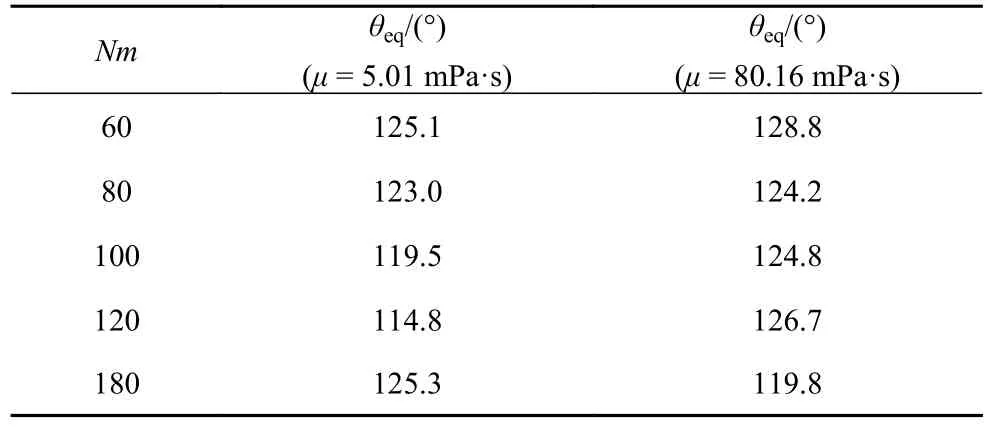
表3 甘油水溶液在网面上的静态接触角Table 3 The equilibrium contact angles of aqueous glycerol solutions droplet on the mesh

如图1 所示,一台Photron Nova S12 高速相机被用来以20 000 帧/秒的时间分辨率和20.6 μm/pixel的空间分辨率拍摄液滴撞网过程.LED 光源配合散光板可以为阴影成像提供均匀光照.

预湿网面是指网面上已经预先有液体存在,普遍存在于实际应用中[34].本文预湿网面的制备如图1(c)所示,使用微量移液器将液体轻放到网面上,通过调整液体量实现预湿高度H的控制,H使用高速相机记录的液滴撞击前图片测量.

2 结果与分析

2.1 液滴撞击干网

2.1.1 最大液指长度

液滴撞击网面后,在网面下产生的液指如果未达到破裂产生二次液滴的临界长度,就会在到达最大长度Lmax后回缩,每一次撞击中产生的最长液指都出现在撞击点附近,如图2 (a)所示.

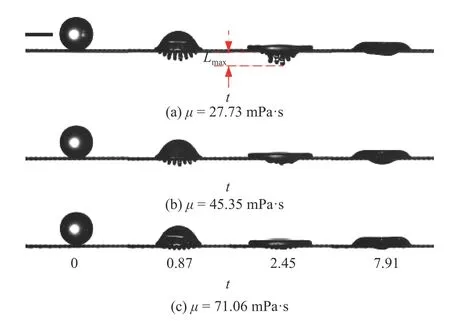
图2 不同黏性液滴撞击网面的演化过程Fig.2 Evolution of droplets with various viscosities impacting meshes of the same parameters

图2(a)～图2(c) 为浓度分别为75% (μ=27.73 mPa·s),80% (μ=45.37 mPa·s),84% (μ=71.06 mPa·s)的甘油水液滴以U=1.97 m/s 的速度撞击80 目网面后的演化过程.图中的无量纲时间t=T/[(D/2)/U]=2TU/D,T为图像对应的实际时刻,以液滴底部接触到网面或液膜的时刻为零点.图2 左上角标尺和本文其他图中的标尺长度均为2 mm.液滴撞击网面后形成液指,到达最大长度后逐渐缩短,并融合成为整体.在整个液滴撞网过程中,网面下形成的液指长度先增大后减小;图2(a) 中75% (μ=27.73 mPa·s)的甘油水液滴在t=2.45 时刻,液指达到最大长度;最大液指长度随黏性增加而减小,说明液体黏性耗散了液滴撞击动能.

图3(a)～图3(c) 为浓度为8 0% (μ=45.37 mPa·s)的甘油水液滴以速度U=1.97 m/s 分别撞击60 目、80 目、100 目网面后的演化过程.液指长度随时间的变化趋势与图2 相同;图3(a)中,t=3.63 时刻,液指达到最大长度;最大液指长度随网孔尺寸减小而减小.

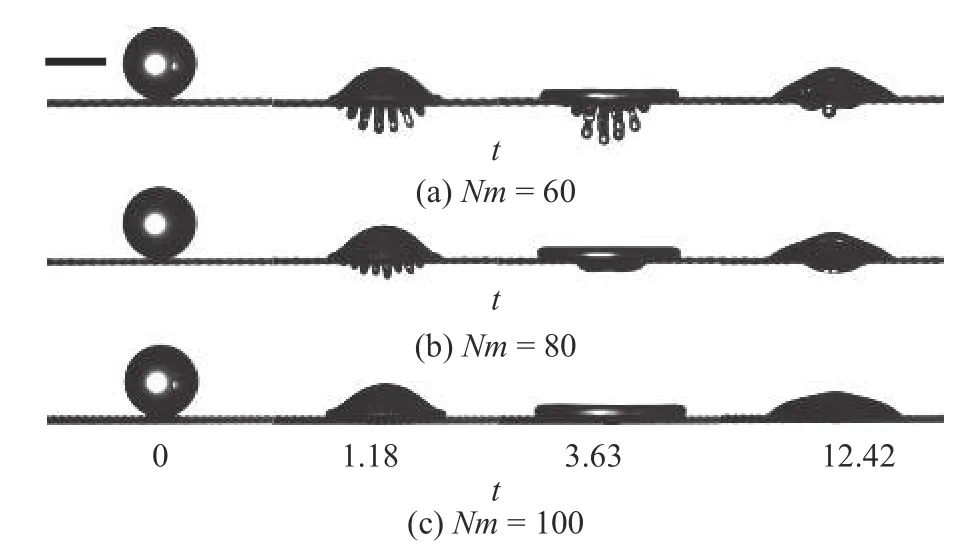
图3 黏性液滴撞击不同网面的演化过程Fig.3 Evolution of viscous droplets impacting meshes of various parameters

图4 为液滴撞击网面后形成的最大液指长度Lmax随液滴黏性μ和网目数Nm变化的曲线,实验中液滴撞击速度U均为 1.97 m/s.图中数据是3 次实验测得数据的平均值,误差线表示标准偏差.需要说明的是,当液滴黏性较小和/或网孔尺寸较大时,液滴撞击后形成完全穿透,液指断裂形成二次液滴而无法测量液指最大长度,所以没有数据,如液滴黏性为5.01 mPa·s 情况下,撞击4 种网面后均形成了完全穿透.由图可知,最大液指长度随液滴黏性的增大而减小,如在Nm=100 情况下,液滴黏性从11.54 mPa·s 增加到80.16 mPa·s,最大液指长度Lmax从0.52 mm 降低至0.03 mm;网线直径接近时,最大液指长度随网孔宽度的增加而增加,如在液滴黏性μ=36.94 mPa·s 情况下,网孔宽度从125 μm(120 目)增加到200 μm (80 目),Lmax从0.10 mm 增加至0.70 mm.实验室空气流动、实验台微振动等随机扰动影响撞击点而产生的随机误差是图4 中Nm=60 和μ=45.37 mPa·s 及Nm=80 和μ=27.73 mPa·s 条件下Lmax标准偏差较大的主要原因,该误差随网孔减小和液滴黏性增大而减小.

图4 最大液指长度随液滴黏性和网目数变化曲线Fig.4 Variations of maximum liquid finger length as functions of droplet viscosity and mesh parameter

图5 为浓度为78% (μ=36.94 mPa·s)的甘油水液滴分别以U=1.00,1.54,1.98 m/s 的速度撞击80 目网面后的演化过程.由图可知,最大液指长度随撞击速度的增加而增加,U=1.00 m/s 情况下Lmax=0.12 mm;U=1.54 m/s 情况下Lmax=0.30 mm;U=1.98 m/s 情况下Lmax=0.59 mm.3 种撞击速度下,液指均在t=0.99 时刻达到最大长度.

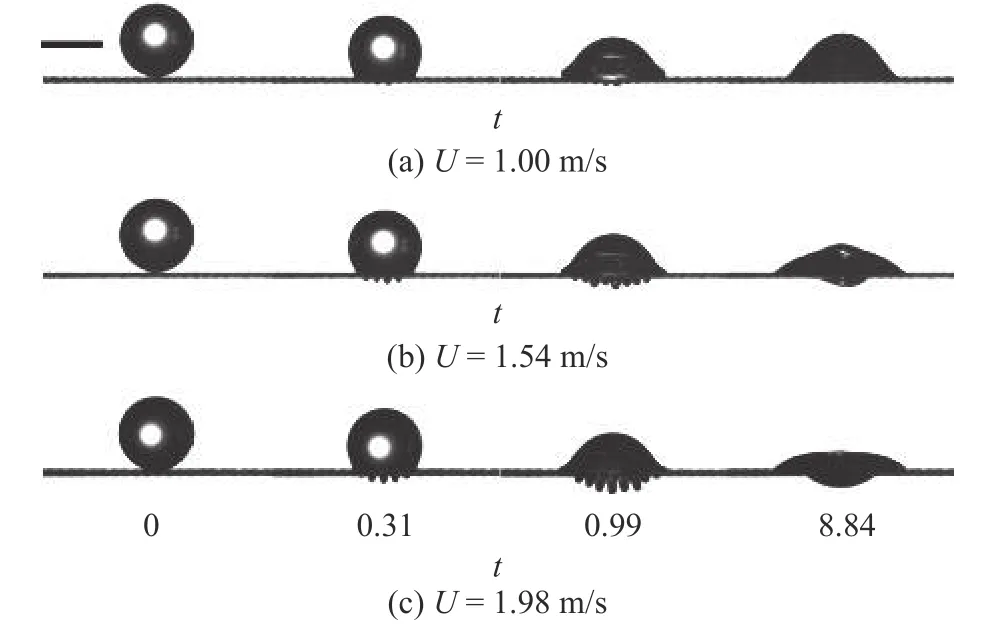
图5 不同速度液滴撞击网面的演化过程Fig.5 Evolution of droplets with various velocities impacting meshes of the same parameters

图6 为液滴撞击网面后形成的最大液指长度Lmax随液滴黏性μ和速度U变化的曲线,图中所有实验均使用80 目网面.与图4 类似,当液滴速度较大时,撞网形成完全穿透而没有最大液指长度数据.由图可知,最大液指长度Lmax随液滴黏性的增大而减小,如在U=1.21 m/s 情况下,液滴黏性从5.01 mPa·s 增加到80.16 mPa·s,最大液指长度Lmax从0.85 mm 降低至0.08 mm;Lmax随撞击速度增大而增大,如在液滴黏性μ=36.94 mPa·s 情况下,液滴速度从0.98 m/s 增加到1.97 m/s,Lmax从0.13 mm 增加至0.70 mm.

图6 最大液指长度随液滴黏性和速度变化曲线Fig.6 Variations of maximum liquid finger length as functions of droplet viscosity and velocity

2.1.2 最大液指长度预测模型

Abouelsoud 等[58]基于4 种黏性的低表面张力液滴撞击1 种网面(接近180 目)的实验结果,建立了一种预测液指最大长度的方法,该方法中的经验系数有4 个值,是分别根据这4 种黏性液滴的实验结果获得的,因此仅能预测这4 种黏性液滴撞击这1 种网面形成的液指长度,无法考虑其他黏性和网孔宽度变化对液指长度的影响,应用受到限制.使用该方法我们计算了9.35 mPa·s 和19 mPa·s 液滴撞击180 目网形成液指的最大长度,如图4 中2 个紫色实心圆所示,预测与实验结果也有偏差.为建立一个更为通用的预测模型,下面我们对液滴撞网时刻和液指长度最大时刻的能量进行分析.

液指达到最大长度时,所有能量转化为液体的表面能.在撞击时刻,初始撞击能量是动能 (ρDω2U2/2)和表面能(2ω2σ)的总和;在撞击过程中,重力对液指做正功(ρgω2L2/2),黏性力对液指做负功(μωLU);在液指达到最大长度时刻,表面能为(σπωL+σπω2/4),其中g为重力加速度,L为液指的实时长度.

在撞击过程中,部分液体穿透网面形成液指,剩余液体在网面上铺展.驱动液体铺展将消耗部分初始撞击能量,因此初始撞击能量只有部分被用于驱动液体穿透网面[58],而前述重力与黏性力做功则全部作用于液指.定义取值范围为0～1 的系数φ与初始撞击能量相乘,表示驱动液体穿透网面的初始撞击能量比例,即φ(ρDω2U2/2+2ω2σ).由能量守恒可得

由实验结果可知,液滴黏性和网孔宽度均影响φ取值,取φ=φ1φ2,φ1～μ1,φ2～ω1,其中μ1=μ/(1 mPa·s),ω1=ω/(1 μm)分别为无量纲黏性系数和网孔宽度.为根据图6 实验数据计算各个黏性系数对应的φ1值,需先确定ω1=200 时的φ2值,此处取φ2=1 (可取任意非零常数,不影响最终φ的拟合公式),由图6 数据可得图7 所示的φ1值,根据这些值可拟合计算φ1的经验公式,如图7 右上所示.根据φ1经验公式计算各个网孔宽度时的φ2值,如图8 中数据点所示,根据这些值拟合计算φ2的经验公式,如图8上部所示.

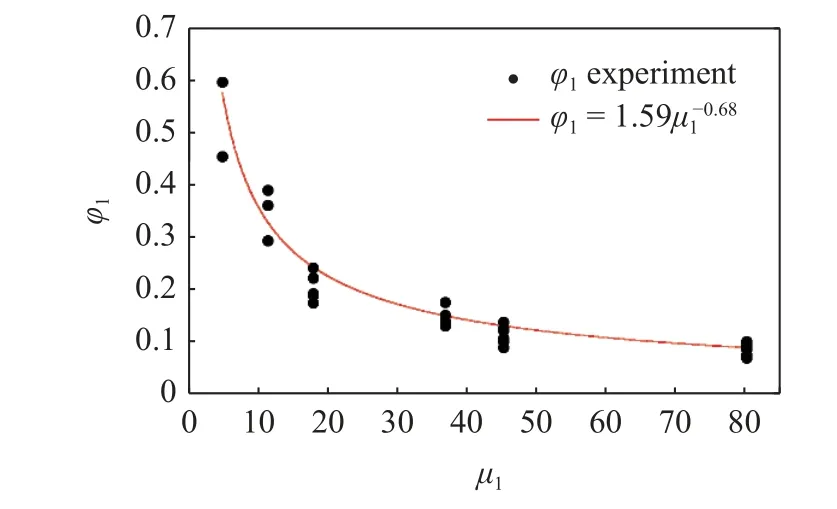
图7 φ1 的实验值与拟合经验公式Fig.7 Experimentally-determined values and fitted empirical formula of φ1

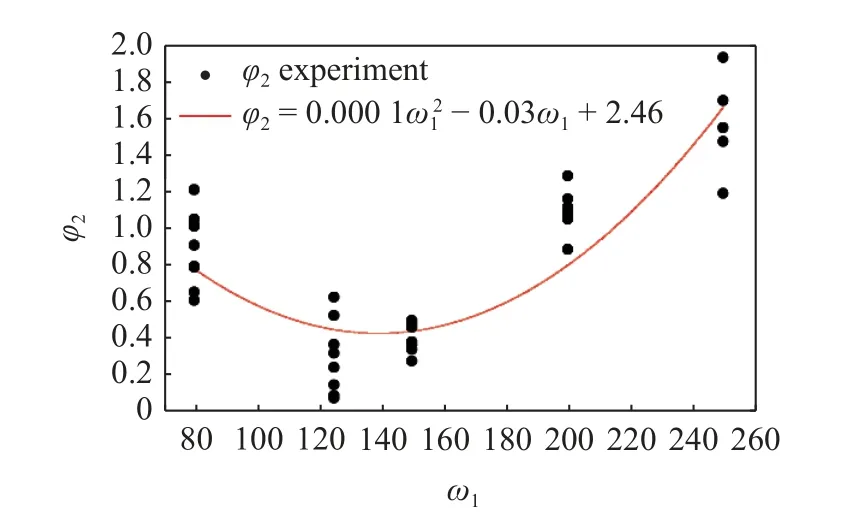
图8 φ2 的实验值与拟合经验公式Fig.8 Experimentally-determined values and fitted empirical formula of φ2

由式(2)可得最大液指长度

由φ=φ1φ2结合φ1和φ2的经验公式得

由式(3)和式(4)可获得各种情况下的最大液指长度预测值,如图4 和图6 中的实线所示.由图可知,该两式计算值与实验结果无论在数值还是变化趋势上都是较为吻合的,为合理预测黏性液滴撞击网面形成的最大液指长度提供了一种方法.

2.1.3 黏性、网面尺寸对撞击产生二次液滴的影响

图9(a)～图9(c) 为浓度分别为50% (μ=5.01 mPa·s),64% (μ=11.54 mPa·s),75% (μ=27.73 mPa·s)的甘油水液滴以U=1.97 m/s 的速度撞击80 目网面后的演化过程.浓度为50% (μ=5.01 mPa·s)和64%(μ=11.54 mPa·s)的甘油水液滴(图9(a)和图9(b))撞击网面后,由于Plateau-Rayleigh 不稳定性导致液指在网面下失稳破碎形成了二次液滴.浓度为75%(μ=27.73 mPa·s)的甘油水液滴(图9(c))撞击网面后形成液指,到达最大长度后逐渐缩短,并融合成为整体.浓度为50% (μ=5.01 mPa·s)的甘油水液滴(图9(a))在t=5.93 时刻,网面下的液指完全破碎形成二次液滴;从图9(a)～图9(b),二次液滴数量随黏性增大而减小,直至图9(c)未出现二次液滴,形象展示了液体黏性对液滴初始撞击能量的耗散.

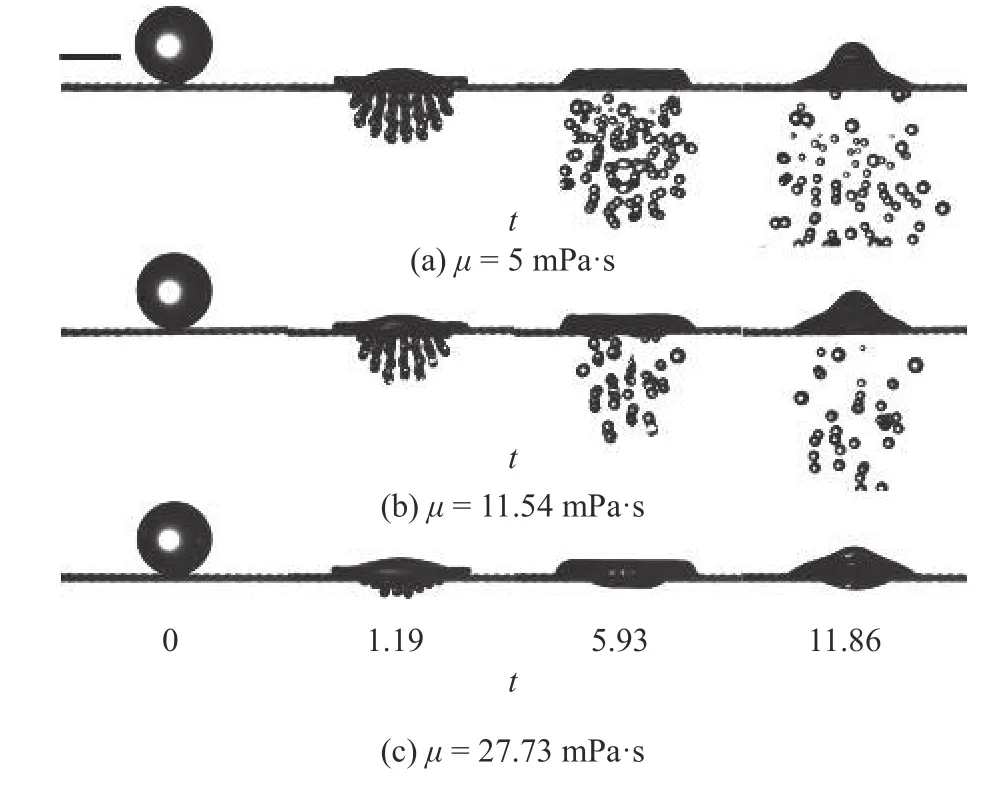
图9 不同黏性液滴撞击网面的演化过程Fig.9 Evolution of droplets with various viscosities impacting meshes of the same parameters

图1 0(a)～图1 0(c) 为浓度为7 0% (μ=18.07 mPa·s)的甘油水液滴以速度U=1.97 m/s 分别撞击60 目、80 目、100 目网面后的演化过程.液滴撞击后随时间的变化情况与图10 相同;图10(a)中t=5.93 时刻,二次液滴完全形成;二次液滴数量随网孔宽度减小而减少直至为0,演示了毛细力在液指形成过程中的阻滞作用.

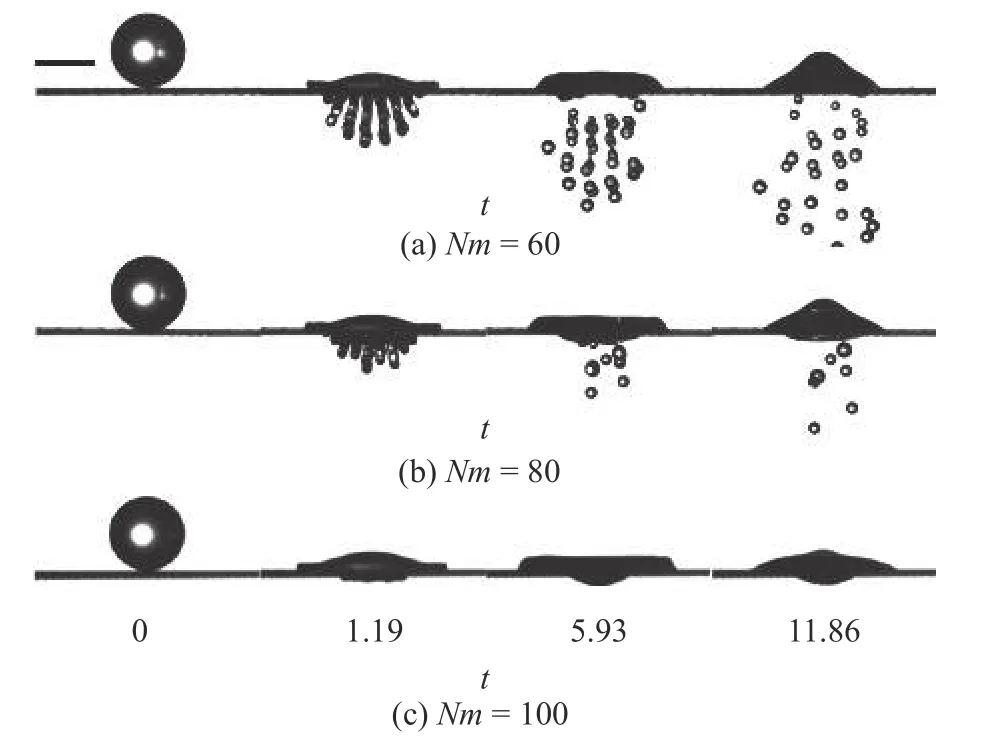
图10 黏性液滴撞击不同网面的演化过程Fig.10 Evolution of viscous droplets impacting meshes of various parameters

使用不同的黏性液滴撞击不同结构的干燥网面,我们获得了临界撞击韦伯数We和临界毛细数Ca,如图11 所示,临界韦伯数随临界毛细数增加而单调增加.图中用不同的符号形状表示不同的网面,不同的符号颜色表示不同的液滴黏性,误差线表示不确定度,实线为理论曲线.

图11 完全穿透临界韦伯数随临界毛细数的变化Fig.11 Variations of threshold We as a function of threshold Ca for completely penetration

2.1.4 产生二次液滴临界条件预测模型

液滴垂直撞击网面时,最容易穿透产生液指和二次液滴的位置是撞击的中心点,液滴的投影面积为～πD2/4,单个网孔结构大小为～(ω+d)2,因此液滴投影面积下的网格数目N=πD2/[4(ω+d)2],实验中使用网面中网孔尺寸最大为60 目,最小为180 目,对应N=34～265,因此可以假设液滴在每次撞击时落点都能保持在其中一个网孔的中心而不是撞击在网线上.

前人已经建立了不考虑液滴黏性的临界韦伯数或者临界速度的预测模型.在无黏情况下,液滴能否穿透网面由液滴的动压～ρU2和毛细压～σГ/A之间的平衡决定[35,38].这里,A=w2和Γ=4w分别表示网面单个开孔的开口面积和周长.液体黏性作用可表示为～μU/w[58].动压可看作是促进液滴穿透的因素,而毛细压和黏性作用都在阻碍液滴穿透网面,可得

式中,m和n是两个常数,需要通过实验确定.根据图11 所示实验结果拟合可得m=8.22 和n=1.45.图11 中黑色实线即为将这两个常数代入式(7)获得的理论曲线,由图可知,理论曲线在数值和变化趋势上均与实验数据吻合较好,可以用于合理预测黏性液滴撞击干燥网面时产生二次液滴的临界参数.

2.2 液滴撞击预湿网面

2.2.1 预湿对最大液指长度的影响

图12 为浓度为70% (μ=18.07 mPa·s)的甘油水液滴以U=1.40 m/s 的速度分别撞击无量纲预湿高度h=0,0.36,0.98,1.58 的60 目网面后的演化过程,其中h=H/(D/2)=2H/D.液滴撞击网面后形成液指,到达最大长度后逐渐缩短,并融合成为整体.从图12(a)～图12(c),网面下形成的最大液指长度随预湿高度的增加而减小,直到图12(d)不再出现,表明网面预湿可完全抑制不完全穿透现象的出现.

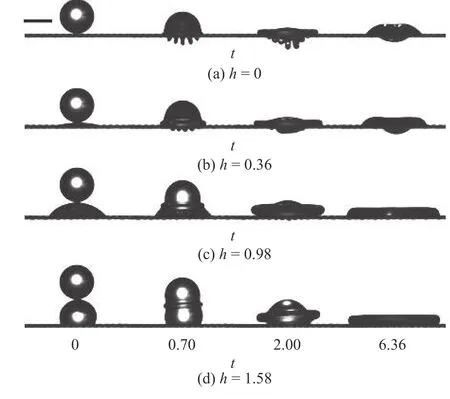
图12 液滴撞击预湿网面的演化过程Fig.12 Evolution of droplets impacting pre-wetted meshes

图13 为液滴撞击预湿网面后形成的最大液指长度Lmax随液滴黏性μ和无量纲预湿高度h的变化,液滴撞击速度U=1.4 m/s,被撞击网面为60 目,图中数据点均为3 次实验的平均值,误差线表示标准偏差,实线为理论预测值.与图3 类似,当预湿高度和液滴黏性较小时,撞网形成完全穿透而没有最大液指长度数据.由图可知,最大液指长度随预湿高度的增大而减小,如在液滴黏性μ=18.07 情况下,预湿高度从0 增加到1.18,最大液指长度Lmax从0.83 mm 降低至0.19 mm;最大液指长度随液滴黏性的减小而增加,如在h=0.47 情况下,液滴黏性μ从80.16 mPa·s 减小到5.01 mPa·s,Lmax从0.13 mm 增加至2.56 mm.

图13 最大液指长度随液滴黏性和预湿高度的变化Fig.13 Variations of maximum liquid finger length as functions of droplet viscosity and prewetted height

2.2.2 最大液指长度预测模型

与低黏度液滴撞击预湿网面[34]类似,黏性液滴撞击预湿网面的演化过程也可以分为如图14 所示的两个步骤,但不同之处是黏性的影响不再能被忽略.图14(a)显示了液滴以速度U撞击预湿液膜,此时,液滴体积为Vd=πD3/6,假设被撞击的预湿液膜为高度为H,直径为D的圆柱体,体积为Vunder=πD2H/4.

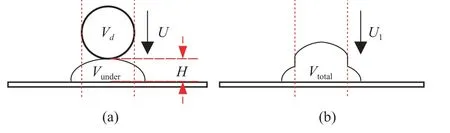
图14 (a) 液滴撞击前及(b) 液滴与液膜融合后流动示意图Fig.14 Sketch of the flow configuration (a) before the impacts and(b) after coalescence of the impacting droplet with the liquid trapped in the mesh

虽然液滴撞击液膜过程中局部流动异常复杂,但是整体来看,是液体流动的垂直分量决定了液滴穿透的类型,因此在分析中可以仅考虑流动的垂直分量.液滴与液滴下方液柱的总体积为Vtotal=Vd+Vunder,融合后速度为U1,如图14(b)所示.撞击过程中液体黏性力为～μDU[58],作用时间由液膜高度H和液滴速度决定U,即～H/U,由动量守恒可得

式(8)化简得

此后,融合的液体可被认为以速度U1撞击干燥网面,将U1代入式(3)可得黏性液滴撞击预湿网面形成的最大液指长度

将图13 的实验条件代入式(10)可得黏性液滴撞击预湿网面后的最大液指长度理论曲线,如图13中实线所示.理论曲线的数值和变化趋势均与实验结果吻合良好,说明式(10)可合理预测黏性液滴撞击预湿网面后的最大液指长度,也进一步说明φ1和φ2两个拟合参数是合理的.

2.2.3 预湿对产生二次液滴的影响

图15 为浓度为50% (μ=5.01 mPa·s)的甘油水液滴以U=1.54 m/s 的速度分别撞击无量纲预湿高度h=0,0.35,0.64,1.63 的60 目网面后的演化过程.液滴在撞击无量纲预湿高度h=0,0.35 (图15(a)和图15(b))的网面后,液指在网面下破碎形成了二次液滴.液滴在撞击无量纲预湿高度h=0.64,1.63(图15(c)和图15(d))的网面后形成液指,到达最大长度后回缩,未形成二次液滴.预湿高度为0 (图15(a))情况下,在t=4.13 时刻,网面下液指完全破碎形成二次液滴;从图15(a)到图15(b),二次液滴数量随预湿高度增大而减小直至图15(c) 未出现二次液滴,表明网面预湿同样可抑制完全穿透现象.

图15 液滴撞击预湿网面的演化过程Fig.15 Evolution of droplets impacting prewetted meshes

图16～图18 分别是浓度为50% (μ=5.01 mPa·s)的甘油水液滴撞击120 目、80 目和60 目网面后是否产生二次液滴的结果相图;图18～图20 分别是浓度为为50%,78%和85% (μ=5.01,36.94,80.16 mPa·s)的甘油水液滴撞击60 目网面后是否产生二次液滴的结果相图,纵坐标为撞击时液滴的雷诺数Re,横坐标为无量纲预湿高度h,h=0 代表干燥网面.图中,蓝色实心圆表示产生二次液滴,红色实心圆表示不产生二次液滴,黑色实线是理论预测的临界曲线.由图可知,完全穿透所需的雷诺数随预湿高度的增加而增大,对于同样的撞击条件,网面预湿可有效抑制完全穿透.

图16 5.01 mPa·s 液滴撞击120 目网面的结果相图Fig.16 Phase diagram illustrating the outcome of 5.01 mPa·s droplets impacting 120 mu meshes

图17 5.01 mPa·s 液滴撞击80 目网面的结果相图Fig.17 Phase diagram illustrating the outcome of 5.01 mPa·s droplets impacting 80 mu meshes

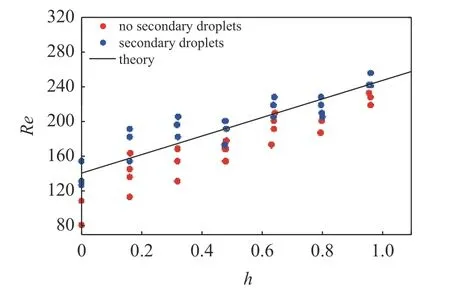
图18 5.01 mPa·s 液滴撞击60 目网面的结果相图Fig.18 Phase diagram illustrating the outcome of 5.01 mPa·s droplets impacting 60 mu meshes

图19 36.94 mPa·s 液滴撞击60 目网面的结果相图Fig.19 Phase diagram illustrating the outcome of 36.94 mPa·s droplets impacting 60 mu meshes

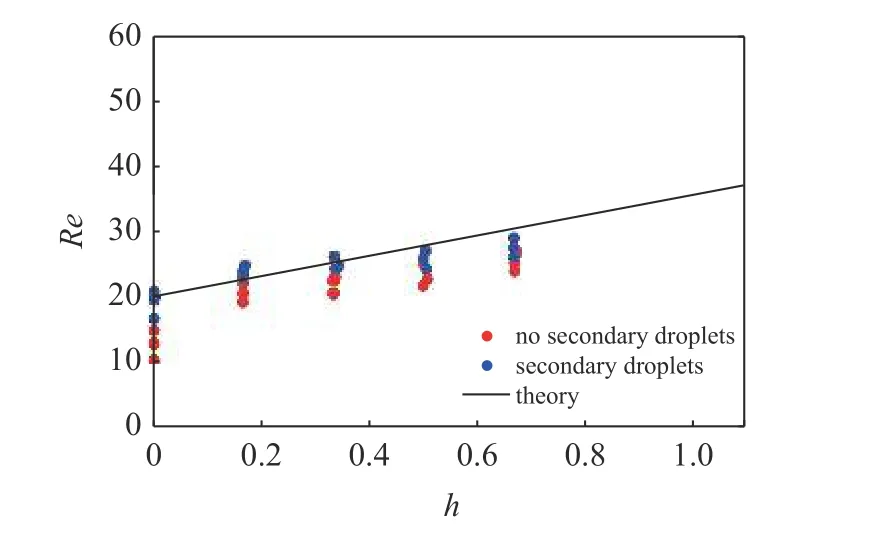
图20 80.16 mPa·s 液滴撞击60 目网面的结果相图Fig.20 Phase diagram illustrating the outcome of 80.16 mPa·s droplets impacting 60 mu meshes

2.2.4 产生二次液滴临界条件预测模型

与最大液指长度预测模型类似,首先引入液体黏性力的影响,通过动量守恒获得液滴与预湿液膜融合后的撞击速度为U1(式(9));此后的撞击过程,可认为是液体以U1撞击干燥网面[34].将U1代入式(6)可得临界速度UP

将式(11)带入雷诺数式可得临界雷诺数

将图16～图20 实验条件带入式(12)可得产生二次液滴所需的临界雷诺数理论曲线,如图中黑色实线所示,理论曲线与实验结果合理吻合,说明理论模型可以合理预测黏性液滴撞击预湿网面产生二次液滴的所需临界雷诺数.

3 结论

本文通过可视化实验研究了10 种不同黏性的液滴撞击5 种不同结构的干燥和预湿网面形成液指和二次液滴的演化规律,通过理论分析了相应机理,并建立了预测模型,获得主要结论如下:

(1)液滴撞击干燥网面后形成的最大液指长度和液滴完全穿透干燥网面所需的临界速度都随网孔宽度减小、液滴黏性增加而减小;

(2)网面预湿可以完全抑制液滴撞击网面后的不完全穿透和完全穿透,预湿液膜高度越高抑制效果越明显;

(3)建立了考虑液滴黏性、网孔宽度和网面预湿的液滴撞击网面后形成最大液指长度及出现完全穿透临界参数的理论预测模型,模型预测结果与实验结果吻合良好.