高速动车组数据驱动无模型自适应积分滑模预测控制

李中奇 周 靓 杨 辉

高速动车组 (Electric multiple unit,EMU) 是由拖车和电力机车组成的动力分布式列车,它已经成为人们日常生活中最重要的交通工具之一.但随着动车组运行速度越来越快、运行环境越来越复杂多变,其车辆之间的非线性效应也越来越显著[1-2].在这种情况下,仅凭借列车司机手动操作无法保证动车组的安全性和其他性能要求.因此,进一步开发列车自动驾驶系统以实现动车组高效运行是非常必要的[3].可靠性高、跟踪效果好的控制器是列车自动驾驶系统的核心,它是实现列车安全、准点、舒适和停车精度等要求的关键.针对动车组控制问题,国内外学者已经提出了许多先进的控制方法,从模型的角度出发,大体上可以分为基于模型和基于数据驱动的控制方法[4].其中基于模型的控制方法研究大多数是从牛顿力学定律出发,通过引入一些假设条件,推导出列车的机理模型从而设计控制方案[5-7].这种思路对单质点列车模型尚且有效,但研究对象是更接近实际情况的多质点动车组系统时则较为困难.同许多复杂系统一样,动车组实际运行过程具有多变量、强耦合以及非线性等特性,使得机理模型的建立异常困难.针对多质点动车组建模难的问题,许多研究开始使用数据驱动建模的方法[8-13].首先设立模型结构,将采集到的各个车厢的输入输出数据通过神经网络训练[8-9]、聚类分析[10-12]、系统辨识[13]等方法获取模型参数,最后对所得模型设计控制方案.虽然数据驱动建模的方法能有效地降低列车系统的非线性和耦合关系,但是其前提是获取列车的模型结构 (输入输出阶数和影响较大的非线性项);其次,各个车厢的输入输出数据不仅数量众多,而且具有较大的偶然性 (由环境因素、系统内扰、执行器故障等因素导致).

综上所述,动车组模型中的基本阻力系数、附加阻力和耦合关系由于诸多不确定因素的影响,导致精确数学模型无法得到;另外,即使建立了简化过后的多质点模型,设计控制器时也必然要考虑到解耦,这无疑增加了计算量和设计难度.因此本文结合动态线性化 (Dynamic linearization,DL) 技术、离散积分滑模控制 (Integral sliding mode control,ISMC) 和模型预测控制 (Model predictive control,MPC) 的优势,使得它们能共同工作,并更好地应用于动车组运行系统,具有重要的理论研究意义和实际应用价值.

侯忠生[14]提出的无模型自适应控制 (Modelfree adaptive control,MFAC) 拉开了 DL 技术的序幕.其大体思想是在系统每个工作点处建立一个虚拟等价的数据模型,根据系统复杂程度可分为紧格式动态线性化(Compact format dynamic linearization,CFDL)、偏格式动态线性化 (Partial format dynamic linearization,PFDL) 和全格式动态线性化 (Full format dynamic linearization,FFDL) 数据模型.这些数据模型仅依赖被控对象输入输出数据,通过在线估计系统的伪偏导数 (伪梯度向量或伪雅可比矩阵) 并最优化系统超前一步输出误差,即可实现数据模型参数的在线更新.随着相应理论的不断发展与完善,基于 DL 数据模型的控制方法已经在许多领域得到了广泛应用[15-18].除了奠基者 MFAC 之外,基于 DL 技术的离散滑模控制 (Discrete sliding mode control,DSMC) 方法亦受到大量关注,学者们在基于数据的建模与优化、数据驱动滑模控制方法改进及参数优化等方面开展了大量的研究.文献[19] 基于 DL 技术和 DSMC指数趋近律,首次提出了无模型自适应准滑模控制方法,并进行了对应的数值仿真实验,但没有考虑实际系统中的扰动等不确定性的影响.在文献[19]的基础上,文献[20] 利用径向基神经网络来估计系统的广义扰动,提出了基于 CFDL 数据模型的自适应滑模控制律,并将其推广至多输入多输出(Multi-input-multi-output,MIMO) 非线性系统,取得了较好的控制效果.但随着系统阶数的增多,滑模控制器数量亦会成倍增多.文献[21] 基于指数趋近律的数据驱动离散滑模控制方法,对智能汽车的速度和位置进行跟踪控制,响应速度和鲁棒性均有所提高.文献[22-23] 充分结合 MFAC 和 DSMC 方法的优点设计复合控制器,其中 MFAC 方法能降低控制器对系统模型信息的依赖,而 DSMC 方法能补偿系统未知外界扰动和未建模动态等不确定性的影响,但复合控制器的稳定性还有待证明.上述方法中,滑模控制律的设计均采用了指数趋近律的处理方法,系统中存在明显的抖振现象.而且,文献[20] 中径向基神经网络有较多参数,加上神经网络的初始权值取随机数,容易导致控制品质下降.

MPC 已成功应用于过程工业的各个领域.然而,对于受连续干扰的系统,仅靠 MPC 无法提供令人满意的效果.考虑到 DSMC 方法的鲁棒性,一些学者尝试将这两种方法结合起来.文献[24] 提出了一种基于积分终端滑模控制和 MPC 的控制方案,使系统在外界干扰下依然能保持良好的鲁棒性.文献[25] 采用 MPC 和 ISMC 实现机械手运动的分层控制.ISMC 用于补偿系统非线性影响,MPC能对状态和输入进行约束.针对受外界干扰的离散时间多输入多输出非线性系统,文献[26] 提出了一种新的基于输出的离散时间积分滑模预测控制 (Integral sliding mode predictive control,ISMPC) 方案,用 MPC 代替了 ISMC 的切换控制.

受上述文献的启发以及考虑动车组实际运行情况,本文首次针对包含外部扰动的 MIMO 动车组系统,提出了一种新的数据驱动离散积分滑模预测控制算法.所提算法基于更符合列车运行特性的FFDL 数据驱动模型,构建了一种新的 ISMC 控制律.为了将系统状态驱动到具有最优运动轨迹的滑模面上,用 MPC 代替 ISMC 的切换控制.这使得ISMPC 能够获得更高的输出跟踪误差精度.在满足一些合理假设的情况下,给出了上述两种方法的严格证明过程.最后,以实验室配备的 CRH380A型动车组仿真实验台对本文提出的 FFDL-ISMC和 FFDL-ISMPC 方法进行仿真测试,比较了两种控制策略的优劣性.

本文的具体贡献主要体现在 4 个方面:

1) 提出了新型的 MIMO 离散 ISMC 和 ISMPC算法,相较于文献[22-23]的方法,系统抖振现象得到了缓解;ISMC 抖振现象良好主要是因为其有切换控制,并使用饱和函数 sat 代替符号函数 sgn;而ISMPC 是因为其在滑模函数中存在两个误差积分权重因子,在跟踪误差和抖振现象中做了折中选择.另外,利用一步延时估计动车组系统参数误差、扰动等不确定因素,实现了较为高效的非线性控制.

2) 为提高控制精度,基于 FFDL 数据模型,结合已设计的 ISMC 和 MPC,进一步推导出积分滑模预测控制方案.与现有组合算法相比,本文的算法不依赖动车组动力学模型,是一种数据驱动控制算法.

3) 与文献[15-17,27]采用的 CFDL 数据模型相比,本文采用的 FFDL 方法综合考虑下一时刻输出变化量与固定长度滑动时间窗口内的输入输出之间的关系.FFDL 数据模型对系统的结构、参数的时变性不敏感.

4) 与已有将 DL 技术运用在列车上的文献[15,28]相比,本文的被控对象为多动力单元列车,更符合实际运行要求.本文所提的方法丰富了列车运行控制理论,可以推广到其他型号的列车系统中 (14 动2 拖的 CRH380AL、4 动 4 拖的 CRH380B、3～5节编组的 TR08 型磁浮列车).

本文的主要结构如下: 第 1 节给出动车组多动力单元模型结构 (仅为列车运行仿真提供数据支持);第 2 节和第 3 节分别提出基于 DL 技术的 ISMC 和 ISMPC 方法,并对其稳定性进行严格的证明;第 4 节和第 5 节分别是仿真分析和总结展望.

引理 1[26].考虑如下标量动态系统

式中,权值常数 0 ＜k1,0 ＜k2＜1,0 ＜α＜1;sig 的含义为 sigα(z)=[sgn(z1)|z1|α,···,sgn(zn)|zn|α]T,sigα(zi)=sgn(zi)|zi|α,sgn 为符号函数.如果|g(t)|＜R,R为任意小的正数,则状态z i(t) 总是有界的且在有限时间内,以下公式始终成立

式中,t*＞0为一个有界时间常数;max 表示取最大值.

1 动车组运行过程动力学分析

动车组运行系统是由多个相对独立的牵引动力单元组成的,每个动力单元又由若干动力机车和拖车分布式组合[2,28].其运行过程中各动力单元除了受自身控制力的作用外,还受到来自相邻单元的车钩影响,动车组纵向动力学分析如图1 所示.图中,中间车厢为装备了牵引单元的动力机车 (轮子为黑色的车厢),首尾两节车厢为拖车.

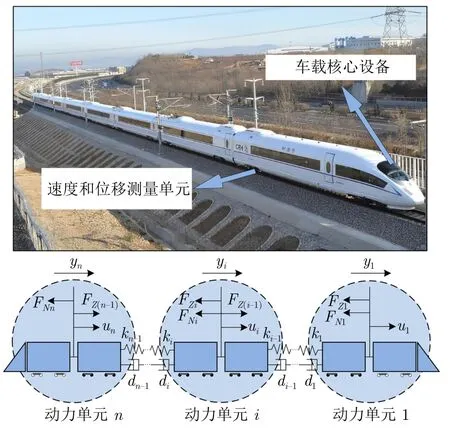
图1 动车组运行过程动力学描述Fig.1 Dynamic description of EMU operation process

根据牛顿运动学定律分析动车组的受力情况,各动力单元上均受到了牵引力或制动力、基本阻力、车间作用力.根据以上分析,可将列车动力单元数学模型表示为[2,28]

ui为列车在不同工况下动力单元i产生的牵引力或制动力;yi和xi分别表示动力单元i的速度和位移;εi为加速度系数,αi表示动力单元i所受的合力;FNi(t) 为列车运行时动力单元i所受到的基本阻力;参数a i,bi,ci分别表示基本阻力系数,均具有高度不确定性;FZi(t) 为动力单元i和动力单元i+1 间的车间作用力,k为相邻动力单元的弹性系数,d为阻尼系数.由基本阻力公式可以看出,动车组速度越快,非线性项对系统的影响则越明显[2,28].参考文献[2],考虑将一阶差分算子应用于系统 (3),得到如下离散时间非线性模型

式中,f i(·) 为非线性函数.

应用常规方案实现列车运行控制时,首要问题是对所有动力单元进行特性分析,将采集到的数据y(t),u(t),x(t)之间的非线性关系建立起来,得到可靠准确的动车组运行模型.然而动车组实际运行中,易受环境、路段变化的影响,列车模型中质量参数、阻力系数、弹簧系数及阻尼系数都存在不确定性,同时模型中还存在着非线性项,导致精确的模型很难得到.针对上述问题,一些研究考虑对列车的非线性部分和车钩作用进行简化,得到了理想情况下的列车模型,在此情况下,若采用非数据驱动控制方法设计控制器需考虑各动力单元的耦合关系,计算量巨大.为此本文设计无模型自适应滑模控制器,对动车组进行速度跟踪控制.

为方便后续动态线性化处理,首先将式 (6) 进行转换.式中所有动力单元的位移项xi都可以用与yi有关的公式表示,而yi又能转换成形如f(y(t),u(t),x(t))的表达式.将式(6) 中所有位移项都转换成与速度和控制力相关的形式,动车组的输入输出数据集合可等效如下 MIMO 离散时间非线性系统

式中,u(t)∈Rn,y(t)∈Rn分别表示系统t时刻的输入和输出;n u,ny分别为系统输入和输出阶数;g(·)为一个非线性且时变的函数.

2 动车组积分滑模控制器设计

2.1 问题描述

首先对列车的输入输出数据集合进行动态线性化处理.常用的 CFDL 方法仅考虑了系统下一时刻的输出变化量与当前时刻的输入变化量之间的关系[18].然而,动车组运行系统的输出不仅仅取决于某一个时刻的控制输入.基于以上考虑,在对数据线性化处理时,可将一个滑动时间窗口内的输入和输出对下一时刻输出的影响都考虑进来,这就是FFDL 数据处理方法.使用该方法可以很好地捕获原系统中存在的复杂动态,并且该动态线性化方法可有效地将系统复杂性分散降低[18].

式中,0 ≤Ly≤ny,0≤Lu≤nu分别为系统输出和控制输入线性化的长度常数,也称为伪阶数.

对动车组系统 (7) 做出如下两个假设:

假设 1[18,29-30].非线性时变函数g(·) 对系统所有偏量的偏导数为连续的.

假设 1 是控制系统设计中对一般非线性系统的一种典型约束条件,适用于一大类非线性系统;假设 2 是一个类线性化条件,即系统输出的变化受一定记忆长度的控制输入和系统输出变化的限制[29].

定理1.如果非线性时变系统 (7) 满足假设 1和假设 2,当时,一定存在一个叫做伪分块雅克比矩阵的参数矩阵Φ(t),使得系统可以等价为 FFDL 数据模型

定理 1 已被严格证明[18],不同的线性化长度常数可以得到不同的 FFDL 数据模型,合理选择长度常数可以提高数据模型对原系统描述时的灵活性.为方便描述,以下令Ly=Lu=1,其他情况类似.

考虑动车组运行过程中存在未知外界扰动、参数估计误差等不确定因素,将动车组的输入输出数据集合重写为

式 中,y m(t+1)=[ym1(t+1),···,ymn(t+1)]T是系统t+1 时刻的输出;d(t)=[d1(t),···,dn(t)]T为包含未知外界扰动、参数估计误差等不确定项的有界广义扰动.

将式 (7) 代入式 (11) 中,可得

根据式 (9) 和式 (12),可得到包含广义扰动的列车 FFDL 数据模型

由于d(t) 是未知的,因此本文基于扰动估计技术,将式 (13) 中的扰动项 Δd(t) 通过其一步延时的值估计

接下来需要对时变参数矩阵Φ(t) 进行实时估计,引入参数估计准则函数[17-18]

根据极小化参数估计准则函数 (15),可得到以下参数估计算法

式中,λ∈(0,2] 为步长因子.

2.2 积分滑模控制器

定义系统输出误差为

式中,y r(t) 为期望输出.

受文献[26] 中算法的启发,考虑引入一种新的积分滑模函数,形式如下

式中,积分权重因子 0 ＜k1＜1,0 ＜k2＜1,可以通过调节k1,k2权衡跟踪大小与抖振现象;两个积分输出跟踪误差项定义如下

随后,基于以下趋近律设计滑模控制策略

结合式 (17)、式 (18) 和式 (21),不难得到

将数据模型 (13) 代入式 (22) 中,可得

由式 (23) 可以推导出等效控制律表达式

当系统的初始状态不在滑模面上或者运动期间出现外部干扰时,独立的等效控制不能驱动系统的轨迹到滑模面[26-27].为了减轻滑模抖振现象,提高系统鲁棒性,设计如下切换控制律

式中,0 ＜γ＜β表示切换增益,γ为一个无穷小的正数.

综上所述,MIMO 动车组滑模控制方案为

注1.本文的等效控制 Δueq(t) 是由滑模函数、滑模趋近律和数据模型共同推导而成,不仅与系统误差有关,还与数据模型的参数矩阵有关;切换控制 Δusw(t) 的系数矩阵与 FFDL 数据模型中有关;而文献[24,26] 中切换控制的系数矩阵与状态空间方程中控制矩阵和输出矩阵有关.此外,不难看出,本文与文献[24,26] 最显著的区别是,本文方法是一种数据驱动方法.

注2.为减轻滑模抖振现象,可以考虑采用如下饱和函数 sat 代替符号函数 sgn

式中,Δ ＞0.当 |si(t)|＜Δ 时,系统的鲁棒性将会受到影响,因此,参数 Δ 的大小应在抑制抖振与鲁棒性之间折中选择.

2.3 算法稳定性分析

假设 3[24,26].当采样时间足够小时,相邻的两个采样间隔广义扰动的变化量不大,即存在一个任意小的正数γ使得以下公式成立

式中,o (γ) 表示γ的同阶无穷小,以下同理.

注3.本文方法的误差收敛值与相邻采样间隔广义扰动的变化量有关,所以只要噪声变量有界,误差收敛值则有界,而噪声在实验过程中是人为设计的 (可控),不影响误差的有界性;另外,排除一些极端突发情况,动车组正常运行过程中,一个采样间隔内的环境因素、系统内扰等变化是可以忽略不计的,所以假设 3 合理.

定理 2.对于具有外部扰动的离散时间 MIMO非线性系统 (11),如果不确定项d(t) 满足假设 3,控制方案采用式 (26),则被控系统满足如下性质:

2) 系统在有限步骤内达到准滑模状态;

3) 输出跟踪误差e(t)=[e1(t),···,en(t)]T收敛到区域 Ωe,其中

式 (30) 展开可得如下形式

将数据模型 (13) 代入式 (31) 中可得

由于时变参数矩阵Φ(t) 有界,令‖Φ(t)‖≤v,v为有界常数.对式 (32) 两边取范数,可推出

对式 (33) 右侧第 2 项取平方

由于步长因子λ∈(0,2],以及µ＞0,不难得到

通过式 (34) 和式(35) 可推出

由式 (36) 可推出,一定存在一个0＜M1＜1的数,使以下不等式成立

将式 (37) 代入式 (33) 中可得到如下不等式

证明 2.系统在有限步骤内达到准滑模状态.

将式 (13) 代入式 (17) 中,可得

将控制律 (26) 代入式 (39) 中,可得

由假设 3 不难得出

将式 (40) 代入滑模函数 (18) 中可得

给出式 (43) 的子元素形式

由式 (44) 不难得出

由式 (45) 可推出

综上所述可知,系统满足如下滑模存在和到达条件

因此,s(t) 单调递减且在有限数量步骤内达到准滑模状态.

证明 3.以下是对输出跟踪误差有界性的分析.

将滑模函数 (18) 代入式 (43) 中

理同式 (44),可以给出式 (48) 的子元素形式

由假设 3 可得

根据引理 1、式 (49) 和式 (50),可得到跟踪误差e i(t) 的收敛性表达式

式中,α,γ,β,k1,k2,b均为有界常数,不难得出系统的跟踪误差e(t) 是有界的.

综上所述,利用控制方案 (26),系统 (11) 的输出能够成功地跟踪期望输出,系统 (11) 的输出也能以期望输出附近的邻域为界.

3 动车组积分滑模预测控制器设计

3.1 积分滑模预测控制器

为了提高系统的输出跟踪控制精度,将所提出的 ISMC 与 MPC 方案相结合.考虑如下 ISMPC定律

式中,Δueq为已设计的等效控制,Δump为 MPC方法生成的最优控制.该控制律使用最优控制Δump将系统状态驱动到滑模面上,等效控制Δueq用于在后续时间内将状态轨迹维持在滑模面上.由式 (24) 中 Δueq可知,ISMPC 总控制量Δu*(t)如下

由于 Δump(t) 是未知的,下一步的目标是基于MPC 方法设计 Δump(t).将数据模型 (13) 代入误差表达式 (17) 中

将式 (24) 中的等效控制 Δueq(t) 代入式 (54)并整理可得

结合式 (18) 和式 (55),给出滑模状态的一步向前预测s(t+1)

因此,2,···,N步向前预测滑模状态为

式中,N是预测长度也是控制长度.对以上N个方程积分得到

N个预测方程可以整理成以下形式

根据上述格式,引入指标函数J2的矩阵形式[26]

式中,θ为权重因子,决定了控制量的大小.将式(65) 代入式 (66),性能指标函数可重写为

极小化性能指标函数 (67),可得到如下控制序列

事实上,式 (68) 中扰动估计误差的值是未知的,用上一采样时刻的扰动估计误差代替是一种可行的方法.由式 (41) 中定义的p(t) 可得

与第 2.1 节的处理类似,Δd(t-1) 可以由得到,那么,p(t-1) 可以由下式得到

通过式 (60)、式 (69) 和式 (70),P(t) 也可以用它的估计代替

所以,控制序列U(t) 可重新写为

由于只需要将预测控制序列U(t) 的第一个控制信号作用到系统中,得到最优控制律为

式中

综合以上,积分滑模预测控制律整体组合为

注4.与文献[24,26] 中的算法相比,本文 ISMPC 算法使用基于 FFDL 数据模型的 MPC,因此也是数据驱动的方法.由于参数矩阵是时变的,在使用 MPC 时则需要进行参数预测处理或者使用向后 (与预测步数一致) 的参数值进行等效替代,控制性能提升的同时复杂度也相应增加.

3.2 算法稳定性分析

定理 3.对于具有外部扰动的离散时间 MIMO非线性系统 (11),在θ=0 时,当不确定项d(t) 满足假设 3,采用式 (75) 的控制方案,被控系统满足如下性质:

1) 任意初始状态,s(t)=[s1(t)···sn(t)]T将收敛到区域 Ωs内,其中

2) 输出跟踪误差e(t)=[e1(t)···en(t)]T收敛到区域 Ωe,其中

证明 4.滑模状态收敛到区域 Ωs内.

首先,当θ=0 时,将最优控制律 (73) 代入式(56) 中,再根据式 (70),可得

根据假设 3,可得出

综上所述,滑模状态s(t) 将收敛到区域 Ωs内.

证明 5.输出跟踪误差e(t) 收敛到区域 Ωe.

首先,当θ=0 时,将最优控制律 (73) 代入式(55) 中,可得

将滑模函数 (18) 代入式 (81) 中

式中

根据定理 3 的性质 1),可推出

将式 (82) 重写为如下的子元素形式

根据引理 1、式 (84) 和式 (85),可以得到输出跟踪误差e i(t) 的上界为

式中,α,γ,k1,k2,b均为有界常数,不难得出系统的跟踪误差e(t) 是有界的.

注5.由本文的系统跟踪误差有界性证明可知,系统误差的最终表达式只与滑模函数的形式以及干扰项的估计误差有关,与系统的数据模型形式无关.当系统干扰项的估计误差有界以及系统满足滑模存在和到达条件时,系统的跟踪误差有界.

注6.本文分析了θ=0 时系统在 ISMPC 方案(75) 下的收敛性.当θ0 时,系统的收敛性还有待证明,将作为作者未来的工作.

4 仿真实现及分析

采用实验室装备的 CRH380A 型动车组实验台对本文提出的 MIMO 数据驱动 ISMC 和 ISMPC 算法进行仿真实验和性能评估,实验装置如图2 所示.通过该平台预留的编程接口输入相应的控制策略,可以将列车运行效果实时显示在虚拟视景设备上,同时记录列车的运行速度、位置、与目标点的距离等信息,模拟真实运行环境.

图2 CRH380A 型动车组模拟实验台Fig.2 Simulation experiment device of CRH380A EMU

CRH380A 动车组有 3 个独立的牵引动力单元,编组方式如图3 所示.该动车组的各节车辆的基本信息如表1 所示[10,28].

表1 CRH380A 型动车组模型参数Table 1 The CRH380A EMU model parameters

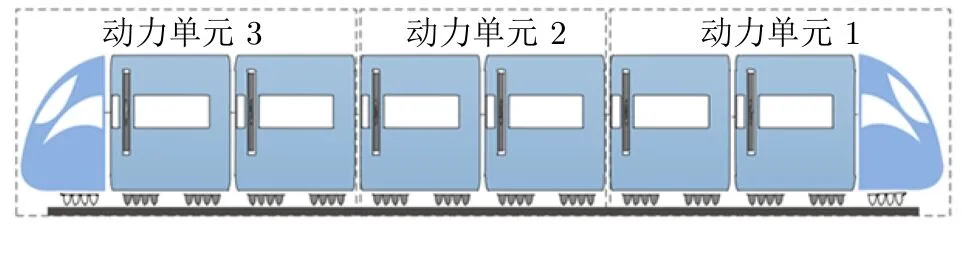
图3 CRH380A 型动车组动力单元分布Fig.3 Distribution of CRH380A EMU power unit

4.1 仿真设置

车辆模拟运行于华东地区的济南西至徐州东路段,速度-位移曲线如图4 所示,其中青色线为限速曲线,红色线为期望的速度-位移曲线,包括牵引、惰行和制动运行模式.匀速段的减速过程表示动车组通过中性段时的滑行模式.图5 为 CRH380A 型动车组牵引/制动特性曲线.

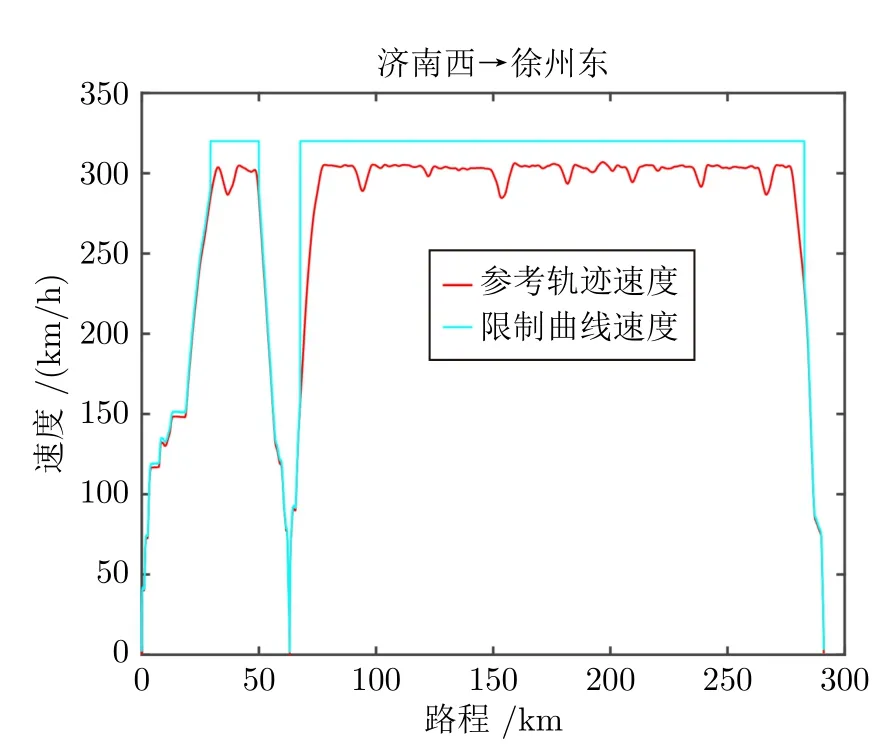
图4 CRH380A 型动车组济南西至徐州东的实际曲线Fig.4 The actual curves of CRH380A EMU from Jinan west to Xuzhou east

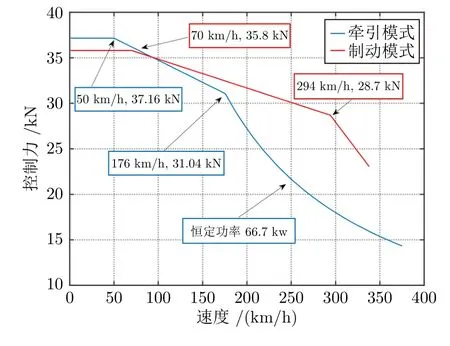
图5 CRH380A 型动车组牵引/制动特性曲线Fig.5 The traction/braking characteristic curves of CRH380A EMU

操作过程中,引入白噪声模拟列车实际运行过程中遇到的外界干扰,用以验证所提算法的鲁棒性.将控制策略以及车辆信息输入到仿真实验台中,记录各方法的列车速度、位置、控制力等信息,并与传统 FFDL-MFAC 和广义预测控制 (Generalized predictive control,GPC) 方法进行对比.

1) FFDL-ISMPC 方法: 系统的初始条件设置为y1(1)=y2(1)=y3(1)=yr(1),Φ1(1)=Φ2(1)=diag{0.5,0.5,0.5}.控制器参数设置为µ=1,λ=0.2,k1=0.5,k2=2,α=0.5,N=10.

2) FFDL-ISMC 方法: 系统的初始条件设置为y1(1)=y2(1)=y3(1)=yr(1),Φ1(1)=Φ2(1)=diag{0.5,0.5,0.5}.控制器参数设置为µ=1,λ=0.2,β=0.05,k1=0.5,k2=2,α=0.65.

3) FFDL-MFAC 方法: FFDL-MFAC 方案可参考文献[18].系统的初始条件设置为y1(1)=y2(1)=y3(1)=yr(1),Φ1(1)=Φ2(1)=diag{0.52,0.52,0.52}.控制器参数设置为µ=1,λ=0.2,δ=1,ρ=0.85.

4) GPC 方法: GPC 方案可参考文献[9-10].系统的初始条件设置为y1(1)=y2(1)=y3(1)=yr(1).控制器参数设置为: 预测时域和控制时域分别为Nv=3,Nu=2;遗忘因子λGPC=0.9.

4.2 各种控制方法的速度跟踪及误差对比

图6 为 ISMPC、ISMC、MFAC 和 GPC 的各动力单元速度-位移跟踪曲线,图7 为对应的速度跟踪误差曲线.由于存在外界扰动,ISMC、MFAC和 GPC 方法的性能受到了较大的影响,收敛性难以保证.平稳路段中,ISMC 的各个动力单元跟踪误差范围在 [-0.274 km/h,0.228 km/h] 之间,由于切换控制的加入,系统抖振程度较轻;MFAC 和 GPC的各动力单元跟踪误差范围分别在 [-0.408 km/h,0.413 km/h] 之间和 [-0.446 km/h,0.438 km/h]之间;在经过分相区等期望速度变化频繁的路段时,MFAC 和 GPC 方法的跟踪性能进一步恶化,误差分别只能稳定在 [-0.627 km/h,0.548 km/h]之间和 [-0.811 km/h,0.862 km/h] 之间.反观 ISMPC 方法,采用新型的积分滑模控制策略,同时,为了将系统状态驱动到具有最优运动轨迹的滑模面上,用 MPC 代替了 ISMC 的切换控制,进一步提升控制性能.各个动力单元跟踪误差范围全程稳定在 [-0.121 km/h,0.132 km/h] 之间,受扰动影响较小,满足速度跟踪精度要求.但相较于 ISMC 方法,系统存在一定的抖振现象,实际工程过程中可在抑制抖振与收敛性之间折中选择.

图6 本文方法与其他方法速度跟踪曲线对比Fig.6 The velocity tracking curves of the proposed method are compared with those of other methods

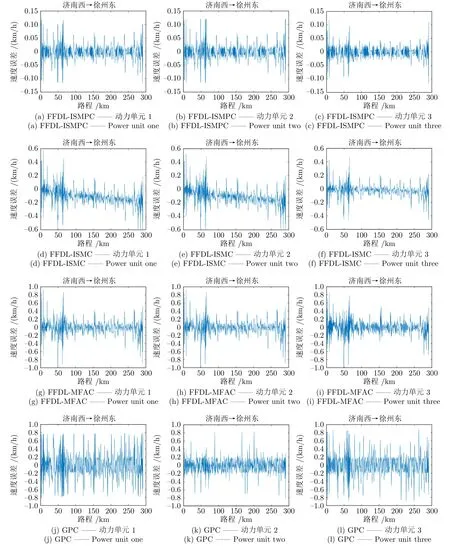
图7 本文方法与其他方法各动力单元速度跟踪误差对比Fig.7 The velocity tracking errors of the proposed method are compared with those of other methods

图8 为 ISMPC、ISMC、MFAC 和 GPC 各动力单元速度分级误差,为图7 的扩展,目的是讨论 4种方法是否符合列车安全速度运行要求.根据 CTCS-3[1-2](中国列车运行控制系统三级) 对速度误差的要求: 当速度小于等于30 km/h 时,速度误差范围不超过 ±2 km/h;当速度大于 30 km/h 时,速度误差应在速度的 2%以内.图8 清楚地阐释了 ISMPC 和 ISMC 方法在所有速度等级都满足 CTCS-3 速度误差要求,而 MFAC 和 GPC 在 30 km/h 和50 km/h 等级处超出速度误差限制,不满足 CTCS-3 速度误差要求.在速度等级 50～300 km/h 范围中,虽然 MFAC 和 GPC 的误差在要求范围以内,但如果出现一些特殊情况 (如过长隧道和长大下坡等特殊路段时),速度容易超出限制,给列车运行带来了一定的安全隐患.

图8 本文方法与其他方法分级速度跟踪曲线对比Fig.8 The proposed method and other methods classify the speed tracking curve

4.3 各种控制方法的控制力和加速度对比

图9 为各个控制方案的控制力变化图,可以看出,在启动、制动、惰行时 ISMPC 和 ISMC 的控制方案各动力单元给出的单位控制力满足恒牵引力启动、恒功率运行等要求[12],控制力范围分别为 [-52 kN,42 kN] 和 [-53 kN,43 kN],在工况过渡阶段,控制力也能以一定的速率缓和变化.同第 4.2 节的分析,由于切换控制的加入,ISMC 较 ISMPC 方法系统抖振现象缓解.MFAC 和 GPC 在启动、制动时存在较大的控制力变化,控制力范围分别为 [-55 kN,47 kN] 和 [-57 kN,58 kN],变化较为频繁且幅值较大,在不节能的情况下,还给列车运行带来一定程度的安全问题.

图9 本文方法与其他方法单位控制力变化对比Fig.9 The variation of unit control force of the proposed method is compared with this of other methods

从图10 各个控制方案的加速度变化可得:MFAC 和 GPC 方法加速度变化过快,范围分别为 [-0.9749 m/s2,0.8687 m/s2] 和 [-1.0124 m/s2,0.8746 m/s2],幅值较大.而采用ISMPC 和ISMC 方法的高速动车组加速度过渡阶段变化平缓,除了启动阶段,范围分别为 [-0.9249 m/s2,0.8187 m/s2] 和[-0.9432 m/s2,0.8210 m/s2],幅值小于 MFAC 方法的同时,满足乘客的舒适度要求[5,12](列车运行的加速度在 [-1 m/s2,1 m/s2] 范围内时,乘客感觉舒适).

图10 本文方法与其他方法加速度变化对比Fig.10 The acceleration changes of the proposed method are compared with those of other methods

综上,本节引入外界干扰,通过速度跟踪误差、控制力变化情况、加速度变化情况验证了 ISMPC和 ISMC 算法的有效性、鲁棒性及各自优劣性所在.

4.4 各种控制方法的若干性能指标对比

进一步,为了更直观分析各个控制器的控制性能,考虑以下若干性能指标对控制器进行评价.

1) 均方误差 (Mean square error,MSE)

2) 积分误差绝对值 (Integral absolute error,IAE)

3) 最大加速度[5,31](Maximum acceleration,MA)

MSE 指标衡量的是观测值与真值偏差,并且对数据中的异常值较为敏感,该值越小,系统跟踪效果越好,IAE 值类似,MA 值反映系统输入的稳定性.各个控制方法的性能指标值如表2 所示,可以看出,ISMPC 和 ISMC 算法的 MSE 值和 IAE 值均小于 MFAC 和 GPC 方法.使用 ISMPC 和 ISMC 算法的列车,MA 值分别为 0.9249 和 0.9432,变化偏小;MFAC 和 GPC 的 MA 值较大,分别为0.9749 和 1.0124,也意味着 MFAC 和 GPC 不满足乘客的舒适性要求,而 ISMPC 和 ISMC 算法可以达到要求.综上,在有干扰的情况下,ISMPC和 ISMC 算法能控制动车组以较小的跟踪误差、稳定的加速度运行.

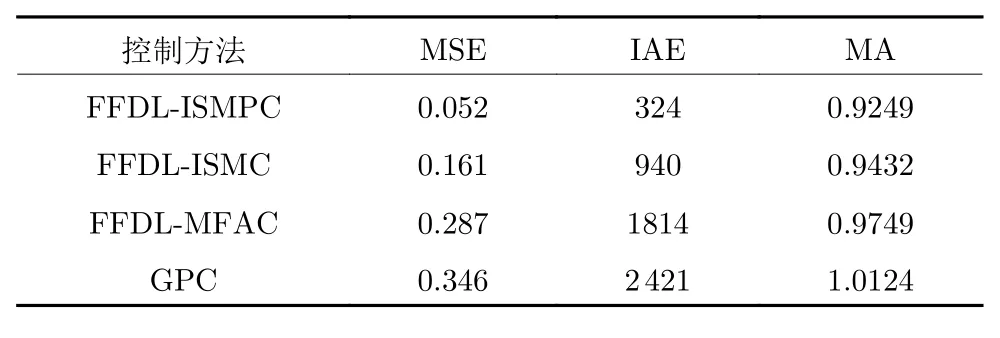
表2 各个控制方法的若干性能指标对比Table 2 Comparison of several performance indexes of each control method

5 结论

本文首次针对包含未知外部扰动的动车组MIMO 系统,提出一种新的数据驱动离散积分滑模预测控制算法.所提算法基于更符合列车运行特性的 FFDL 数据驱动模型,构建了一种新的 ISMC控制律.为了将系统状态驱动到具有最优运动轨迹的滑模面上,用 MPC 代替了 ISMC 的切换控制.在满足一些合理假设的情况下,给出了上述两种算法的严格证明过程.最后,以实验室配备的 CRH-380A 型动车组仿真实验台对本文提出的 ISMC 和ISMPC 算法进行仿真测试.通过与 MFAC 和 GPC对比,仿真结果表明:

1) ISMPC 实现了比 ISMC、MFAC 和 GPC方法对给定速度-位移曲线更高精度的跟踪控制,误差范围在[-0.121 km/h,0.132 km/h] 之间,满足列车速度误差要求,确保列车安全准时运行;

2) ISMPC 算法控制力变化更平稳,各动力单元加速度变化范围均在 [-0.9249 m/s2,0.8187 m/s2]之间,满足乘客的舒适度要求;

3) 由于用 MPC 代替了 ISMC 的切换控制,ISMPC 相较于 ISMC 算法,系统存在一定的抖振现象,实际工程中应该在抑制抖振与收敛性之间折中选择;

4) ISMC 相比于 ISMPC,跟踪性能会差一些,但是由于切换控制的存在,它的抖振情况又比 ISMPC 要好;ISMPC 所使用的方法是基于 FFDL数据模型的 MPC 方法,因此也是数据驱动的方法.由于参数矩阵是时变的,在使用 MPC 时则需要进行参数预测处理或者使用向后(与预测步数一致)的参数值进行等效替代,控制性能提升的同时复杂度也相应地增加了;此外它的抖振现象比 ISMC 要明显.如何使得该算法在跟踪性能良好的情况下无抖振现象,将作为作者未来的工作重心.

进一步,在本文的基础上,作者将在未来进行以下研究:

1) 在引入外部干扰的基础上,考虑不同车厢类型和延时影响;

2) 考虑采用神经网络方法对本文提出的控制算法进行参数优化;

3) 近年来,许多学者开始关注列车多智能体系统的协调控制和编队控制问题.其目标是通过系统中各智能体的相互协作,提高运行效率,防止事故发生[32-33].因此,在未来的工作中,作者将研究具有多智能体的高速列车无模型自适应控制.