利用直达波计算稳健的深水OBN双检匹配算子

王明星,张庆淮,朱立彬

(1.中石化石油工程地球物理有限公司国际业务发展中心,北京 100020;2.中国海洋大学海洋地球科学学院,山东青岛266100)

目前,海洋油气勘探开发面临更加复杂的海底作业环境,传统的拖缆或海底电缆(ocean bottom cable,OBC)等海洋地震数据采集方式难以满足复杂海底区域作业要求。基于海底节点(ocean bottom node,OBN)的海洋地震数据采集则不受采集电缆与地震船连接的束缚,可以灵活地设计观测系统,能够实现大偏移距、宽方位(全方位)地震数据采集[1-3]。此外,四分量OBN采集的地震数据提供了包含纵波和转换波在内的更多的地震信息。因此,OBN地震采集越来越成为海洋油气勘探,尤其是在复杂海底情况下的主要采集方式。

数据成像是OBN地震勘探面临的主要难题之一,其中鬼波压制和上、下行波场分离是一个长期存在的挑战。波场分离是通过将地震数据中水检记录的压力波场和陆检记录的垂直质点速度波场进行合并,然后再将合并后的波场分离成上行波和下行波。最初,人们直接通过垂直叠加,或者使用固定的匹配系数进行双检振幅匹配后再通过合并水检数据和陆检数据来压制鬼波,再进行波场分离。这种方法极不精确,不能适应水深和水底介质等因素的变化,波场分离效果不好。为此,人们提出了许多双检求和、分离上、下行波场的方法。如童思友等[4]提出了基于维纳滤波的双检数据鬼波压制技术。高少武等[5-6]对海上地震数据双检匹配做了大量研究,总结出多种上、下行波场分离方法。BARR[7]提出时空变的匹配算法,计算出每个检波点的每一个采样点的振幅匹配系数并对陆检数据进行匹配后,再与水检数据合并,分离上、下行波场。这种算法也是目前主流商业软件中主要的OBC/OBN地震数据波场分离算法。SOUBARAS[8-9]提出一种经典的匹配算子求取算法,首先,对水检和陆检数据进行共检波点叠加及交互鬼波化,然后,采用这两个交叉鬼波化后的叠加数据求取匹配算子,从而避免了极性相反的下行波对求取双检匹配算子的干扰。这种方法之所以成为经典,是因为它为人们提供了一种稳定的匹配算子求取方法,也是目前浅水地震数据处理中较好的鬼波解决方案。但是这种方法在交互鬼波化后,依然没有办法完全避免下行波对匹配算子求取的干扰。

随着OBN在海洋地震数据采集中的应用越来越广泛,做好接收点鬼波压制,更好地保留地震数据的带宽和分辨率,更好地分离上、下行波场,对改善海上地震数据成像质量至关重要。目前OBN采集的地震数据基本上利用反射波计算双检匹配算子,但在深水OBN采集中,利用反射波求取双检匹配算子面临许多局限性。利用直达波求取匹配算子的方法有其独特的优势,可以避免噪声对匹配算子计算的影响,从而求取稳定的双检匹配算子,达到更好地分离上、下行波场,改善地震资料波场特征的目的。

1 问题的提出

深水OBN地震勘探采用多分量检波器接收,将水检数据和陆检垂直分量数据进行合并,可以压制鬼波,分离上、下行波场。

双检合并最理想的情况是水检和陆检具有相位相同的上行波和相位相反的下行波,上、下行波场之间没有绝对振幅、频率和时间差异,如图1所示。图1a 为水检理论记录;图1b为陆检理论记录;图1c 为双检合并后的结果;图1d为水检记录的一维傅里叶变换,显示了水检记录接收点侧鬼波的频率陷波问题;图1e为陆检记录的一维傅里叶变换,显示了陆检记录接收点侧鬼波的频率陷波问题;图1f为双检合并记录的一维傅里叶变换。可见双检合并后,鬼波得到压制,由鬼波造成的频率陷波点消失,说明双检合并能对鬼波频率陷波进行补偿。因此,在水检和陆检地震数据没有振幅、频率和相位差异的前提下,水检和陆检记录的波场中鬼波的频率互补,经过双检合并可以压制鬼波,分离上、下行波场。

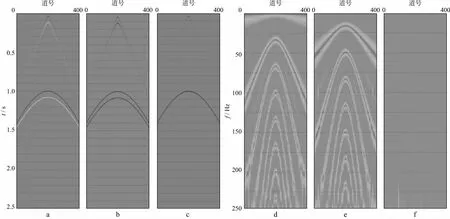
图1 理想情况下的双检合并a 水检记录; b 陆检记录; c 双检合并后记录; d 水检记录一维傅里叶变换; e 陆检记录一维傅里叶变换; f 双检合并后记录的一维傅里叶变换

但是,在实际OBN地震数据中,水检记录的压力波场和陆检垂直分量记录的速度波场并不会达到理想状态,两者之间会存在振幅、频率、相位上的差异[10],而且地震数据中总会存在各种各样的噪声,这些因素导致直接对双检数据进行合并时难以取得较好的鬼波压制效果。从20世纪90年代开始,地球物理学家们就认识到了这个问题,对地震数据净化进行了许多研究[11],并对水陆双检合并问题进行了大量探索,寻找合并前的双检匹配方法。但这些技术大多基于两种检波器数据中的反射波求取双检匹配算子,Soubaras方法[8]就是其中的典型代表。下面以该方法为例,分析利用反射波求取双检匹配算子在深水OBN波场分离中可能遇到的一些挑战。

基于水检和陆检垂直分量双检合并的理论公式[12],SOUBARAS提出了基于交叉鬼波化的双检合并算法[8],采用估算一个将水检与陆检垂直分量相匹配的滤波器,解决水底反射率变化、检波器不同、检波器耦合不良等因素导致的信号差异问题。该双检合并方法可以分解为3个步骤,即双检匹配、波场分离和微屈多次波压制。考虑到深水OBN地震勘探中下行波具有明显的照明优势,而压制微屈多次波仅针对上行波,因此,这里不考虑微屈多次波压制,仅介绍其中的双检匹配和波场分离。波场分离采用公式:

(1)

式中:U是上行波场;D是下行波场;H是水检记录的压力波场;G是陆检记录的速度波场;fc是用于校正陆检的匹配算子。

计算fc之前,为了排除下行波的干扰,Soubaras方法首先使用(2)式计算交叉鬼波化的水检波场H′和陆检波场G′:

(2)

式中:Z=e-iωΔt表示水层中地震波双向垂直移动的算子;Δt是水中传播的双程延迟时间。交叉鬼波化后,水检和陆检数据具有相同的时间,但幅度和相位不同,可通过最小化交叉鬼波化后的水检和陆检之间的差异来求解双检匹配算子fc:

(3)

在几米到几十米,甚至100m以深的浅海地震勘探中,很难提取稳定的直达波信号,Soubaras用交叉鬼波化后的反射波求取水陆检的匹配算子,为人们提供了一种稳定的双检匹配算子计算方法。但是,在深水OBN地震数据处理中,用反射波计算双检匹配算子会面临以下4个方面的挑战。

1) 李斌等[13]指出,陆检垂直分量含有大量不易去除的转换波噪声,如何避免这些噪声对求取更稳定的双检匹配算子的影响需要继续深入研究。ZHANG等[14-15]提出陆检垂直分量中的横波泄漏是深水OBN双检合并面临的一个挑战,并分别通过利用所有4个分量数据的降噪方法[16-17]和只使用两个纵波分量的自适应减法[18-19]来消除陆检垂直分量中不需要的横波,取得了较好的效果。图2a是水检记录;图2b 是陆检垂直分量记录,可以明显观察到泄漏到垂直分量上的横波能量,如图2b中的红色箭头所示。

图2 OBN数据中的横波泄漏噪声a 水检记录; b 含横波泄漏的陆检记录

2) OBN地震数据中含有包括随机噪声在内的各种噪声,含噪声反射信号的相关运算不可避免地会影响双检匹配算子的稳定性。

3) 深水OBN地震数据中浅层上行波的照明不好,利用上行反射波的双检匹配方法会面临反射波能量太弱的挑战。

4) 深水OBN地震数据的静校正非常困难,使得利用反射波共检波点叠加的双检匹配方法面临极大挑战。

受以上因素的制约,有必要研究替代反射波的深水OBN双检匹配算子计算方法。

2 用直达波求取双检匹配算子的方法

在OBN地震采集中,如果达到一定深度,就可以获得一定偏移距的稳定的直达波信号。根据水深、地震波在海底传播的速度和水中传播的速度,可以确定直达波信号的偏移距范围。另外,直达波完全在水中传播,因此我们可以根据水深和偏移距获得准确的直达波校正时差,从而实现直达波信号的同相叠加。在深水地震勘探中,直达波与其对应的水底多次波有一定的时间间隔,选取小时窗直达波可以避免噪声对求取匹配算子的影响。理论和实践证明,水、陆检波器波场的差异子波可以用直达波的差异子波代替,因此,可以直接用直达波来求取水检和陆检数据的匹配算子。

在接收点水深hr、激发点水深hs、地震波在水中传播的速度vw和沿海底的传播速度vb已知的前提下,初至为直达波的数据的偏移距范围为(0～x),其中x由下式判定:

(4)

在偏移距(0～x)范围内选取一定数量的双检数据,用图3所示流程求取双检匹配算子,进行波场分离。

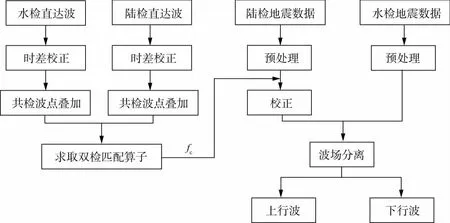
图3 利用直达波求取双检匹配算子及波场分离的流程

用直达波求取双检匹配算子、进行双检合并、分离上下行波场的主要步骤如下。

1) 在共接收点道集上由(4)式定义的范围内选取一定偏移距范围的直达波。深水OBN直达波一

般没有被噪声污染,因此不需要太多的地震道用于共检波点叠加。

2) 根据零偏移距接收点水深h0r、激发点水深hs、偏移距x和地震波在水中传播的速度(1500m/s左右)计算校正时差,对双检数据分别进行时差校正。

(5)

然后对时差校正后的双检数据分别进行共检波点叠加,得到各检波点的叠加数据,如图4所示。

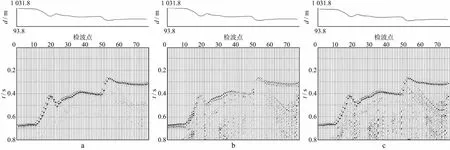
图4 含有直达波的共检波点叠加剖面a 水检记录的共检波点叠加; b 陆检记录的共检波点叠加; c校正后的陆检记录共检波点叠加

3) 根据检波点水深、激发点水深和地震波在水中传播的速度获取计算时窗的中心点时间tm=(h-hs)/vw,向上向下扩展得到匹配算子的计算时窗tm-τ1～tm+τ2,时窗长度τ1+τ2不宜太大,经验值为100～300ms。

4) 输入水检和陆检共检波点叠加数据,在选取的时窗内用最小二乘方法求取每一个检波点的双检匹配算子fc。

argmin‖H-fc*G‖2

(6)

5) 用求取的匹配算子fc校正陆检数据,使水检和陆检数据匹配。

6) 水检和陆检数据匹配之后,用公式(7)进行双检合并,分离上下行波场。

(7)

式中,fc是利用直达波求取的匹配算子。用直达波求取的匹配子波与用反射波求取的匹配子波相位相反,因此,请注意(7)式与(1)式的区别。

3 应用效果分析

图4是含有直达波的共检波点叠加结果。图4a为水检数据的共检波点叠加结果;图4b为陆检数据的共检波点叠加结果;图4c为利用求取的匹配算子校正后的陆检数据共检波点叠加结果。由图4可见,在校正之前,水检、陆检的共检波点叠加有明显的相位和振幅差异;校正之后,水检和陆检的直达波波形趋于一致。

图5分别是利用反射波交叉鬼波化后求取的双检匹配算子(Soubaras方法)和利用直达波求取的双检匹配算子。不难看出,两种算子具有相反的相位。Soubaras方法由于噪声等因素的干扰计算出的算子不稳定,而本文方法求取的匹配算子稳定。

图5 两种方法求取的双检匹配算子对比a Soubaras方法求取的双检匹配算子; b 本文方法求取的双检匹配算子

利用匹配算子校正之后,水检和陆检数据的直达波相似程度越高,双检合并的效果就越好,因此,经过计算校正之后水检直达波和陆检直达波的相似系数来对匹配算子的匹配效果进行评价。图6是用Soubaras方法和本文方法计算的匹配算子校正后水检和陆检共检波点叠加的相似系数。图6a为Soubaras方法双检匹配后的水检、陆检相似系数,可以看出,相似系数大部分介于0.6～1.0之间。图6b为本文方法校正后水检、陆检相似系数,可见绝大部分相似系数都在0.9以上。二者对比说明,在深水OBN地震数据双检匹配中,本文方法校正后的水检和陆检数据的匹配度更高,具有明显优势。

图6 两种方法双检匹配后的相似系数对比a Soubaras方法双检匹配后的相似系数; b 本文方法双检匹配后的相似系数

图7是一对水检、陆检记录的匹配及合并效果对比。其中,图7a是原始陆检记录;图7b为原始水检记录;图7c为本文方法校正后陆检记录。可以看出,原始水检、陆检记录存在明显的振幅、相位差异;校正后,水检、陆检下行波相位一致,上行波相位相反,振幅接近。图7d和图7e分别为利用(7)式进行双检合并分离波场后的上、下行波场记录,可以看出波场分离效果很好,上行波波场中看不到明显的下行波能量,下行波波场中的上行波残留也非常小。

图7 双检数据的校正与合并a 原始陆检记录; b 原始水检记录; c 校正后陆检记录; d 合并后上行波场; e 合并后下行波场

图8是应用本文方法对海底起伏剧烈的记录进行波场分离的效果。图8a为陆检记录;图8b为水检记录;图8c和图8d分别为应用本文方法进行波场分离后的上、下行波场记录。经过对比可以看出,即使海底崎岖导致经海面反射的下行波同相轴严重偏离了双曲线形态,利用本文方法依然可以很好地分离上、下行波场。

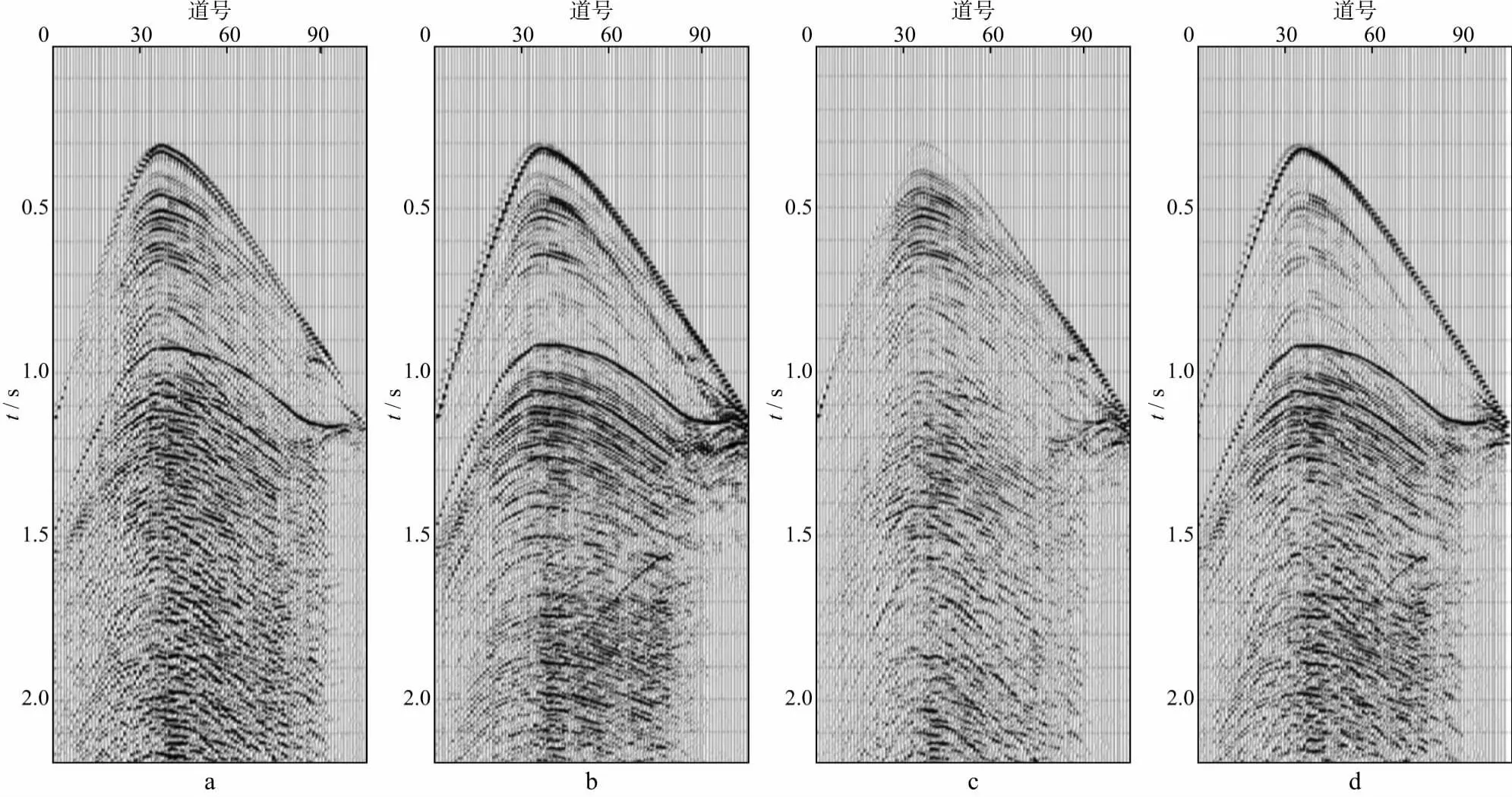
图8 海底起伏剧烈的双检数据波场分离效果a 陆检记录; b 水检记录; c 上行波记录; d 下行波记录

为了验证本文方法在计算深水OBN双检匹配算子中的优势,分别对水、陆检记录直接合并、利用商业软件进行振幅匹配后再合并、利用Soubaras方法进行双检匹配后再合并,以及利用本文方法进行双检匹配后再合并的效果进行了对比,如图9所示。图9a 是水检、陆检直接合并的结果。可以看出,双检直接合并波场分离效果不好,在上行波场中存在明显的下行波;图9b是利用商业软件进行了时空变双检振幅匹配后合并的结果,由于没有进行相位匹配,波场分离效果依然很差,分离后的上行波场中存在明显的下行波;图9c是应用Soubaras方法,即利用反射波进行双检匹配后合并的结果,可以看出,Soubaras方法较好地解决了双检匹配问题,波场分离效果较好,但是在上行波场中依然可以看到残留的下行波能量;图9d是采用本文方法求取双检匹配算子,并用该匹配算子进行双检匹配后合并的结果,可以看出,本文方法波场分离效果最好,在上行波场中,几乎看不到下行波能量。

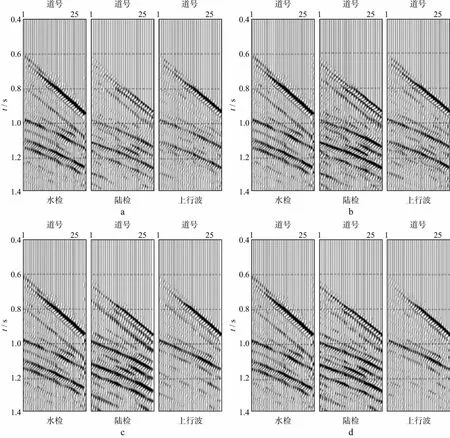
图9 不同双检合并效果对比a 水、陆检直接合并; b 振幅匹配后双检合并; c Soubaras方法双检合并; d 本文方法双检合并

图10是深海OBN水检数据、陆检数据和利用本文方法进行波场分离后的上行波、下行波数据快速QC叠加剖面对比。图10a是水检数据的叠加剖面;图10b是陆检数据的叠加剖面;图10c是波场分离后的上行波叠加剖面;图10d是波场分离后的下行波叠加剖面。在水检叠加和陆检叠加剖面上可以明显观察到海底多次波和近海底反射多次波同相轴;波场分离后的上行波叠加剖面上由于排除了下行波的干扰,叠加效果更好。与上行波叠加剖面相比,深海OBN数据的下行波叠加剖面(图10d)优势更加明显,海底和地下反射的叠加效果明显好于上行波。

图10 深海OBN双检数据和波场分离后的数据叠加剖面对比a 水检数据叠加; b 陆检数据叠加; c 上行波叠加; d 下行波叠加

4 结论与认识

1) 在深水OBN地震数据的上、下行波场分离中,用反射波求取双检匹配算子的方法受一系列因素的制约,求取的匹配算子不够稳定,从而影响上、下行波场分离效果。

2) 如果水深达到一定深度,在OBN地震数据中就会有相对稳定的直达波,选取一定范围的直达波来求取双检匹配算子,可以避免噪声对计算结果的干扰,而且几乎不受海底起伏和上行波照明的影响,求取稳定的双检匹配算子,更好地分离上、下行波场。

3) 用直达波求取双检匹配算子不适用于浅水OBN地震数据,但是,直达波计算深水OBN双检匹配算子的方法给我们带来启示,利用浅水低信噪比地震数据中反射波之外的其它较稳定的信号可以成为计算双检匹配算子的潜在方案。