一种确定海底地震仪位置与等效海水速度的多维扫描法

李 华,刘佳仪

(1.同济大学图书馆,上海200092;2.长江大学工程技术学院,湖北荆州434022)

受海流影响,海底地震仪(包括OBN,OBS,为方便论述以下统称为OBS)在设计点位投放以后,在下沉过程中会发生横向漂移。水深越深、流速越大、水文情况越复杂,着底点的漂移量会越大或越不确定。因此,OBS的定位是主动源海底地震勘探的关键步骤之一。OBS的定位有两种方法:①利用OBS声学通讯,但这种方式受声学通讯有效范围制约,且需要多方位测量,定位效率低,受水速影响误差大,目前较少使用;②利用地震数据的冗余到时信息,这种方法定位效率高,但定位精度受水速误差、海底深度以及到时拾取误差等影响。

为此,很多研究对地震定位方法进行了改进。为了提高定位精度,李丽青等[1]和徐云霞等[2]对实测数据进行线性动校正,根据直达波同相轴拉平效果确定OBS的位置。TRABATTONI等[3]利用船上噪声,采用频谱分析技术实现OBS的定位,定位精度较高,但需要准确的船舶自动识别系统(AIS)数据和尽量多且宽频的噪声信号。为了克服海底深度和海水速度未知的影响,OSHIDA等[4]利用初至波走时,结合精确的水深测量和全局搜索方法实现OBS的定位。马德堂等[5]根据初至波到达时,首先利用搜索法确定海水速度,再利用三点定位法和最小平方法确定OBS位置,同时减小了拾取误差、炮点误差和水速误差对定位精度的影响。DU等[6]利用初至波走时,首先,结合最小二乘法和蒙特卡洛方法对OBS进行定位,然后,利用二次曲线拟合获得平均水速与水深。BENAZZOUZ等[7]则利用初至波到达时,构建关于OBS坐标与水速的超定方程,分两步获得OBS坐标与水速。马力等[8]联合利用海水直达波与海底折射波,采用模拟退火法迭代求解实现浅水OBN的二次定位,相较于仅利用单一直达波走时,定位精度有所提高。但可以看出,以上地震定位方法要么假设海水速度恒定,但需要已知准确的海底深度与海水速度;要么采用分步法逐次实现OBS的定位与海水速度的估计,实际应用都存在挑战。由于海水的盐度和温度分层不均匀,海水速度存在垂向变化[9-10],海水中存在不同尺度涡旋等物理海洋现象,也导致海水速度在横向上具有非均匀性[11]。在重定位方法中假设海水速度恒定或视为已知而不参与反演都会引入海水速度模型误差,导致定位不准确,直接影响后续的多分量重定向处理[12],进而影响后续的多分量建模与成像。王忠成等[13]利用直达波走时,构建OBS坐标与等效海水速度的超定方程,利用最小二乘法迭代求解OBS坐标与等效海水速度,提高了定位的精度,但梯度导引类方法存在多参数串扰的风险。白杰等[14]结合水下机器人投放与初至波二次定位技术,获得较传统海面投放方式精度更高且点位偏移量更稳定的布放效果,但布放及回收效率大幅降低。

为此,本文提出了一种简单、快速、精准的多维扫描法,可以同时实现OBS的定位、海底深度估计及等效海水速度反演。

1 方法原理

受盐度、温度和压力变化的影响,海水中的地震波传播速度存在不均匀性,特别是在深水环境中,不均匀性尤其明显,速度范围通常在1450～1550m/s[15]。目前仍缺乏海水速度建模的有效手段。所以,在海洋地震调查中海水通常被视为均匀速度层或按照Munk模型[16]给出,导致海底声呐测深所得到的海底深度通常存在误差。在海上地震勘探中,受水流影响,OBS着底位置往往偏离投放的设计位置。利用不准确的海水速度和海底深度进行OBS重定位必然存在位置偏差。为此,提出着底位置、海底深度和等效海水速度同时反演的方法。利用共接收点道集上拾取的海水直达波走时t0,在三维空间与速度共4个维度上进行扫描,寻找如下二范数的最小解,即:

(1)

其中,

(2)

(3)

式中:i为共OBS道集中的炮点下标;sxi,syi,szi为任一炮点坐标;rx,ry,rz为扫描的虚拟OBS坐标,其中,rz代表海底深度;v为等效海水速度;tc为虚拟OBS对应的理论走时。需要指出的是,由于海水速度变化不大,通常在1450～1550m/s,故此处假设射线路径为直射线,进而等效海水速度即相当于射线路径方向上的平均海水速度。另外,根据Munk模型[16],假设海水速度局部呈水平层状分布,那么根据简单的几何关系(图1)可以得到,局部等效海水速度在各个偏移距上相同(公式(4))。而整个区域的横向非均匀海水速度模型通过对多个OBS对应的局部等效海水速度叠加再拟合即可获得:

(4)

图1 等效海水速度计算示意

根据(1)式～(3)式可导出rx,ry,rz,v4个参数的核函数表达式((5)式～(8)式)。不难发现,rx,ry,rz3个位置参数的敏感性依赖于单一方向的偏移距与炮检绝对距离d之比(总是小于1),故敏感性不超过10-4,且偏移距越大,水平位置敏感性越大,海底深度敏感性越小。说明可以用大偏移距数据定位OBS,小偏移距数据反演水深;等效海水速度的敏感性依赖于炮检绝对距离d,在大于1500m的超深水情况下,即使利用小偏移距数据,3个位置参数的敏感性也可以达到10-3,偏移距越大敏感性越强。也就意味着等效海水速度最容易被准确地估计出来,3个位置参数次之,大偏移距数据更有助于等效海水速度的反演。

(5)

(6)

(7)

(8)

该多维扫描法的技术流程如图2所示,具体实现步骤为:

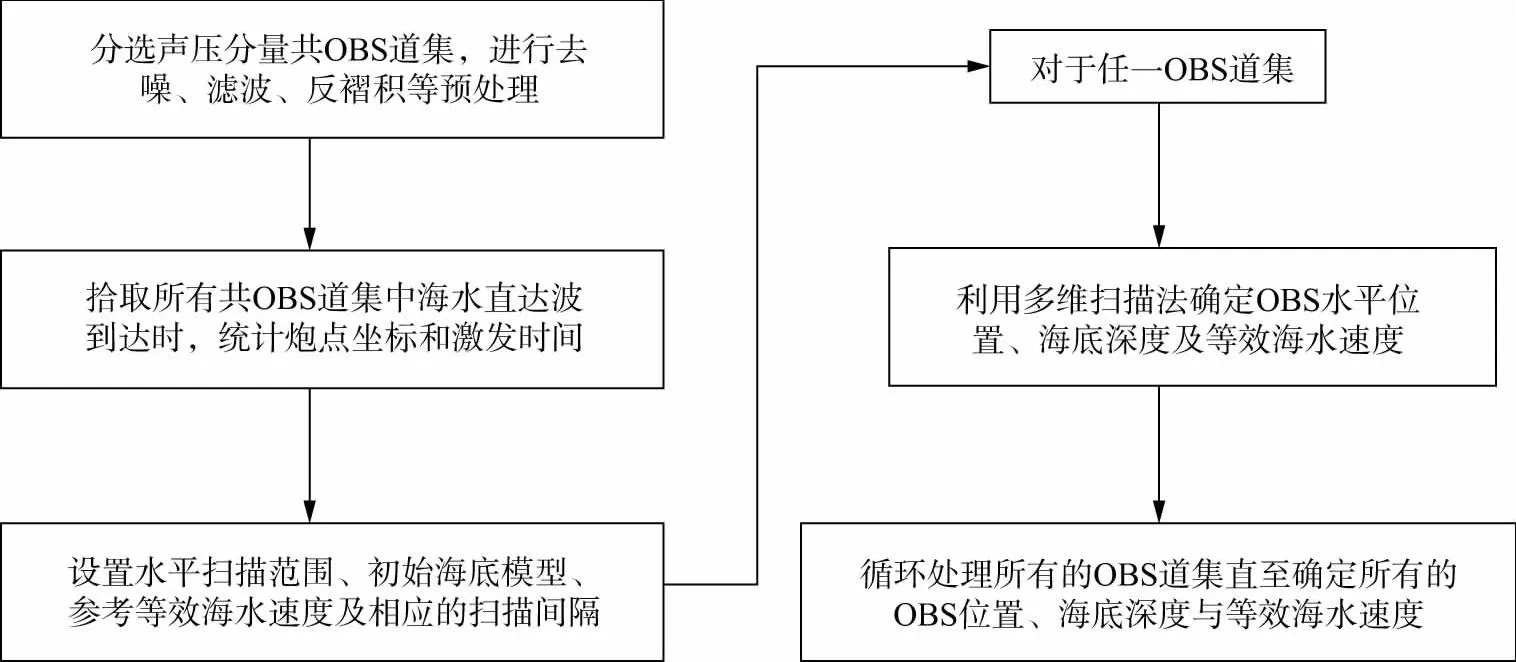
图2 多维扫描法的技术流程

1) 对原始地震数据进行滤波、去噪和反褶积等预处理,并将预处理后的地震数据分选为共检波点道集(即共OBS道集)。

2) 拾取所有共检波点道集中海水直达波震相(或同相轴)的到达时t0,统计炮点坐标sx,sy,sz和激发时间。需要注意的是,在小偏移距内,海水直达波即为初至波,但随着偏移距的增大,海水直达波不再是初至走时,而位于海底的折射波震相(或同相轴)之下。所以,一定要确保拾取的是连续的海水直达波震相(或同相轴)。同时,需要保证拾取的直达波走时、统计的炮点坐标和激发时间尽量精准。

3) 根据观测系统的覆盖情况及水文情况预设空间水平扫描范围,保证OBS的着底范围在预设扫描范围内。同时根据船上测深结果提供初始海底深度模型以及等效海水速度参考模型。权衡定位精度与计算能力,设置以上参数的扫描间隔。间隔越小、精度越高,但计算量越大。

4) 对于任一OBS道集,以投放点水平坐标为中心,在设定的正负水平范围内,按照设定的水平间隔逐次变化OBS水平坐标rx,ry,进行一级循环;以投放点水平坐标所对应的海底初始深度为中心,在设定的正负垂直范围内,按照设定的垂直间隔逐次变化OBS深度rz,进行二级循环;以给定的参考等效海水速度为中心,在设定的正负范围内,按照设定的间隔逐次变化参考海水速度,进行三级循环;对该OBS道集所涉及的所有炮点逐个扫描,进行内层循环,按照(1)式～(3)式累积计算每个虚拟OBS的目标函数φ(rx,ry,rz,v)。

5) 取前三层循环中使得目标函数取最小的rx,ry,rz,v即为该道集所确定的OBS坐标、海底深度以及等效海水速度。

6) 循环处理所有的OBS道集直至确定所有的OBS位置、海底深度与等效海水速度。

2 数值实验

2.1 二维理论海水速度模型

根据实际OBS采集观测系统特点,我们设置以下三维模型实验:模型大小为x方向(370000,373000),共3000m;y方向(2092000,2103000),共11000m;海水深度为2750～2850m;在模型中心2000m×2000m范围内布设9台OBS于水平海底,具体坐标如表1所示。参考海水速度为1460～1540m/s;海面以下8m处以100m间隔沿二维线自北向南均匀激发93炮,模拟OBS接收到的海水直达波走时作为观测数据。为了更加接近实际情况,观测数据保留<1ms的误差,即观测数据到时为整毫秒时间。多维扫描时,参考海水速度设置为1500m/s,扫描范围±40m/s,扫描间隔为1m/s;参考海水深度为2800m,扫描范围±50m,扫描间隔为1m;水平方向在整个模型范围内扫描,扫描间隔为5m。理论模型实验多维扫描结果如表1所示。利用单进程每次实验的扫描用时380s。实验表明,当真实水平坐标落在扫描网格点上时,所有参数都可以被准确地反演出来(1～5组),尽管观测数据有较小的误差存在;当真实水平坐标没有落在扫描网格点上时(更加符合实际情况),OBS水平位置的平均误差为7.5m,海底深度平均误差为3m;所有情况下,等效海水速度的值都可以被准确地反演出来。由表1可见,3个位置参数的敏感性相当,而等效海水速度的敏感性最强,与以上理论认识相吻合。该理论测试同时表明,本文提出的多维扫描OBS定位方法计算速度快且定位精度高。

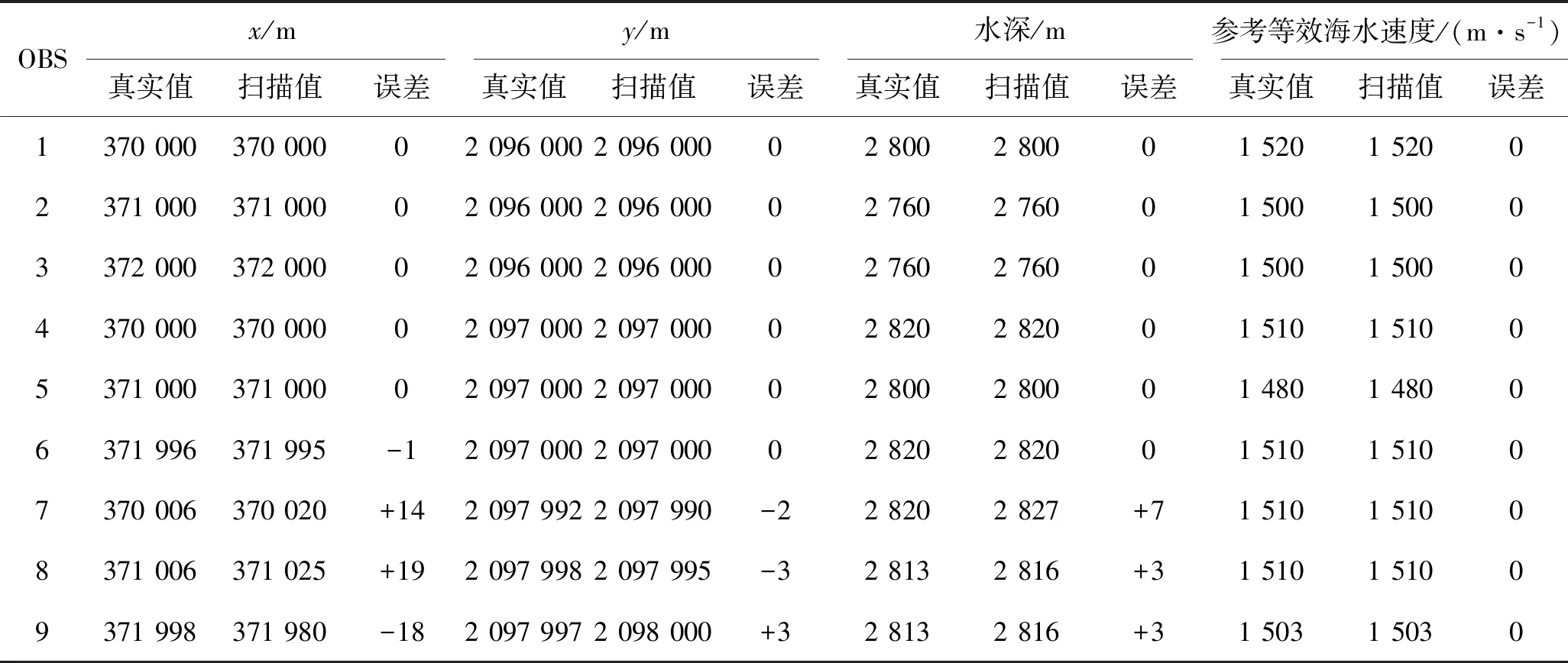
表1 理论模型实验多维扫描结果

需要说明的是,为了进一步提高扫描效率,可以适当加大参数的扫描间隔,但这样会导致参数估计误差的增大;在计算能力允许的情况下,考虑到海水深度与速度一般局限于较小的范围内,因此深度参数与速度参数的扫描间隔可以尽量小,如以上实验中间隔设为1m和1m/s,就可以得到较好的反演精度。

2.2 二维实际OBS资料

将本文提出的方法应用于我国南海荔湾凹陷附近的3个实际OBS数据。观测系统覆盖范围为x方向(370000,373000),共3000m;y方向(2087000,2107000),共20000m;海面以下8m处以100m间隔沿二维线自北向南均匀激发164炮;在共OBS声压分量道集上拾取海水直达波走时作为观测数据,观测数据到时为整毫秒时间(图3)。多维扫描时,参考海水速度设置为1500m/s,扫描范围±40m/s,扫描间隔1m/s;根据声呐测深建立参考海底深度模型,深度范围为2600～3000m,深度扫描范围在参考深度基础上±50m,扫描间隔1m;水平方向在整个测线范围内扫描,扫描间隔10m。南海实际OBS数据多维扫描结果如表2所示。利用单进程每次实验的扫描用时200s。多维扫描结果表明,OBS整体向西南漂移,x方向偏移量皆为300m左右,y方向偏移量皆为100m左右,与当时的水流方向相符。水深估计值2760～2800m,水速为1490～1510m/s。利用定位前、后的坐标分别对道集进行线性动校正,动校正前、后海水直达波线性动校正曲线如图4至图6所示。其中,红色线表示利用投放点坐标动校正之后的结果;绿色线表示利用多维扫描法重定位后坐标动校正的结果。由图4至图6可见,重定位坐标动校正后海水直达波震相更平,说明重定位坐标的相对准确性。直达波震相不完全水平,仍有一定起伏,可能是由于海水的水平层状假设无法得到满足,随着偏移距的增大,等效海水速度不再适用。

表2 南海实际OBS数据多维扫描结果

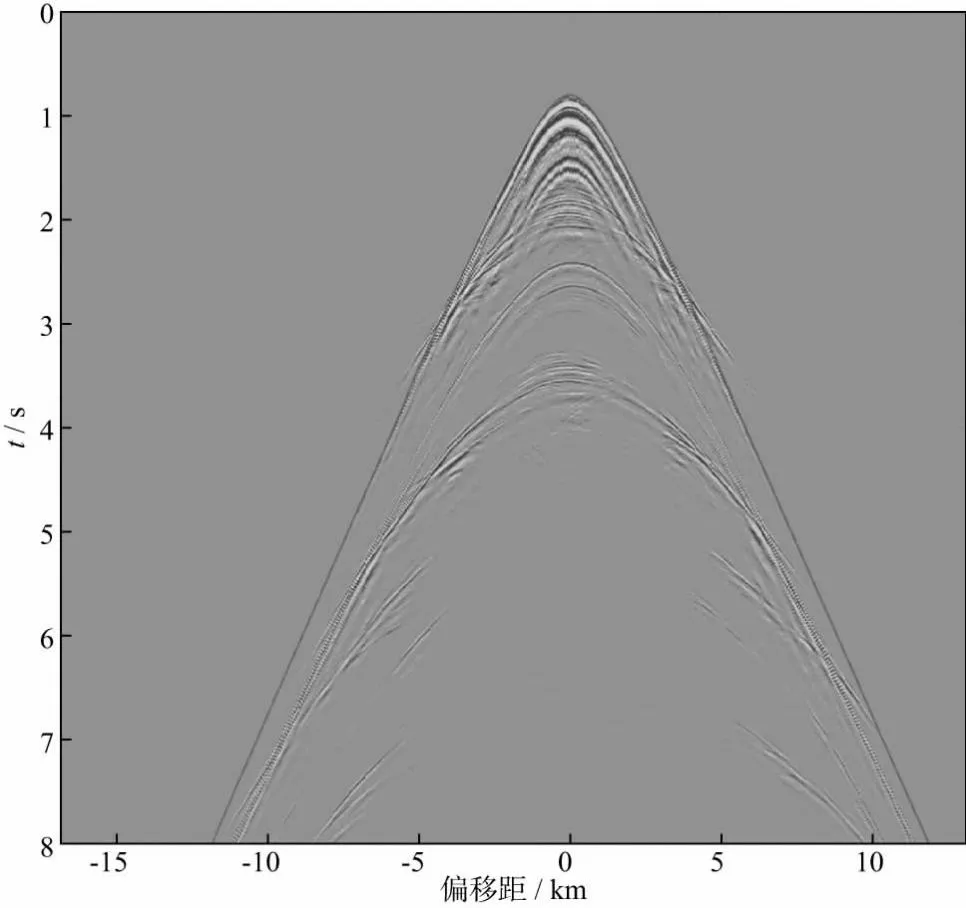
图3 南海实际资料含海水直达波拾取结果的共OBS声压分量道集

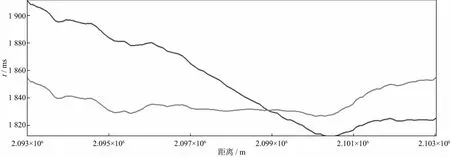
图4 南海实际资料OBS01重定位前(红线)、后(绿线)海水直达波线性动校正曲线

图5 南海实际资料OBS02重定位前(红线)、后(绿线)海水直达波线性动校正曲线

图6 南海实际资料OBS03重定位前(红线)、后(绿线)海水直达波线性动校正曲线

3 讨论

除本文的多维扫描方法外,理论分析部分展示了另外一种分步反演策略的可行性。首先,利用大偏移距数据扫描反演等效海水速度,然后,利用小偏移距数据扫描确定海底深度,最后,利用大偏移距数据获得水平坐标。

利用理论实验的模型和数据进行分步反演策略测试。第1步反演等效海水速度时需要初始OBS坐标和初始海底深度。此处,初始OBS水平位置从共检波点道集中最小海水直达波走时所在的炮点坐标中提取,误差控制在±100m/s以内。初始海底深度设为2800m;第2步更新海底深度时,利用第1步确定的等效海水速度和初始OBS坐标;第3步利用前两步确定的等效海水速度和海底深度更新OBS水平坐标。利用单进程每次实验的扫描用时小于1s。理论模型实验分布扫描结果如表3所示。可见等效海水速度误差约为10m/s,海底深度误差约为30m,水平坐标误差约为70m。与前文的多维扫描法相比,分步策略反演精度降低了10倍,但效率提升了近400倍。反向说明在计算能力允许的条件下,为了获得尽量高的反演精度,还是需要采用本文提出的多维扫描反演策略。

表3 理论模型实验分步扫描结果

另外,考虑到直达波走时拾取难免存在拾取误差,本部分进一步测试数据误差对反演结果的影响。在前述理论模型实验中引入更大的随机数据误差(<10ms),其它参数保持不变,多维扫描结果如表4所示。由表4可见,OBSx方向平均误差达到140m,y方向平均误差达到21m,海底深度平均误差达到17m,说明以上参数受拾取精度影响较大;但等效海水速度仍可以被较准确地反演出来,受拾取误差影响较小。基于核函数定量分析(5)式～(8)式,不难发现实验数据的合理性。x方向的误差大于y方向与观测系统在y方向的优势排列有关。总之,与传统利用直达波走时进行定位的方法相同,本文方法的反演精度也严重依赖于走时拾取的准确度。

表4 理论模型实验数据含误差(<10ms)情况下的多维扫描结果

需要说明的是,本文数值实验的反演精度是在接近3000m水深的超深水情况下获得的。在浅水情况下,为了节约成本通常采用OBN采集,本文方法和取得的认识同样适用。甚至,考虑到数据拾取误差和采集孔径变小,扫描密度更高,浅水情况下会获得更高的反演精度。

4 结论

传统OBS定位方法通常依赖海水速度与海底深度的预测精度,为此提出了一种多维扫描法。除水平坐标维度外,经过增加海底深度和等效海水速度两个维度的扫描,实现OBS水平位置、海底深度与等效海水速度4个参数的同时反演。

二维理论海水速度模型实验验证了该方法的有效性和理想的反演效果。实际OBS资料测试也表明,该方法可以在实际应用中提供准确、高效的4个参数的反演结果。

反演精度同时依赖于扫描密度,即扫描密度越高,反演精度越高。在地震勘探尺度上,通常水平方向扫描间隔10m,在参考海底深度基础上垂直方向扫描间隔1m,在参考海水速度基础上等效海水速度扫描间隔为1m/s,即可以获得相当高的反演精度。本文方法的假设前提是海水中射线路径近似直线,且局部海水速度为水平层状,后续将考虑海水横向非均匀性较强的情况下,同时反演OBS坐标与非均匀海水速度的方法。