基于 MATLAB分析的动车组跨接电缆计算
李春波,周安德,李丰收,李西宁
中车株洲电力机车有限公司,湖南 株洲 412001
0 引言
跨接电缆是动车组车辆间实现电气线缆连接的关键部分,主要功能是实现列车供电电路、控制信号、网络信号的连接等。跨接电缆的安装方式及线缆长度等因素对车辆的运行安全性和可靠性十分重要。跨接电缆在运行过程中的受力及活动情况复杂是影响电缆寿命的主要原因,而线缆长度的选择是影响可靠性的关键因素之一:跨接电缆太长,可能超出列车限界造成线缆刮蹭磨耗;跨接电缆太短,则会出现拉升现象,造成连接器和线缆脱离,影响电气和安全性能。因此,如何设计跨接电缆的长度是行业内重点研究的内容。 目前,国内跨接电缆的设计尚无理论支持,一般是通过试验模拟车辆实际运行状态,多次试验后确定跨接电缆长度;部分动车组跨接跳线则是通过分析各种工况,模拟计算得出线缆长度。而本文基于电缆的各方向受力分析,借助悬链线方程,搭建跨接电缆长度计算模型,确定跨接电缆长度,在无试验条件情况下,可指导跨接电缆的设计确定。
1 现有跨接电缆计算方法
现有项目的跨接电缆计算方法大多为估算,根据线缆固定点之间的距离、受力分析、车辆运行线路条件分析等给出一个范围取值,计算过程较为繁琐,耗时费力,该方法没有实际模型做支撑,估算长度也根据设计师因人而异,无法形成统一的计算方法。 一般是根据固定点最近距离与最远距离不断调整弯曲半径以使其满足最低点限界要求和最小弯曲半径要求,然后根据极限距离估算出线缆长度,最后确定一个取值范围[1]。
2 基于悬链线方程的跨接电缆计算方法
本文借助悬链线,使用MATLAB进行车辆跨接电缆长度的计算设计,建立适当的数学模型,提出了基于悬链线方程的跨接电缆计算方法。
2.1 采用悬链线方程的跨接电缆长度分析
悬链线是将1根绝对柔软、无刚性的绳子,两端挂在垂直的墙上,自然悬垂形成的曲线[2],其方程为:
(1)
即:
y=acosh(x/a)(双曲线函数)
(2)
式中:x∈R,且x=0时,y=a,a为常系数。
在实际的工程应用中,一般可转化为
y=a[cosh(x/a)-1]
(3)
在跨接电缆长度计算中引入悬链线方程,以固定点处的曲线斜率与安装面垂直为约束,使得电缆实际形状拟合悬链线曲线,则电缆两端固定点处附加弯曲应力为0,计算出电缆长度,线缆受力情况如图1所示[3]。
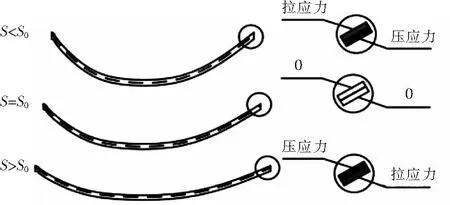
图1 3种工况下电缆固定点附近的受力情况
假定对于某条自由状态下长度为L0、2个固定点距离为S0的电缆,在静止时,S等于S0,此时电缆固定点附近所受到的附加弯曲应力为0。车钩压缩状态下,S小于S0,车钩拉伸状态下,S大于S0,这2种工况下电缆固定点附件所受到的附加弯曲应力最大[3]。
基于以上分析,可知悬链线方程适用于跨接电缆的计算。以固定点处的曲线斜率与安装面垂直为约束,使电缆实际形状拟合悬链线曲线,则电缆两端固定点处附加弯曲应力为0,可有效提高电缆寿命[4]。
2.2 数学模型的建立
由于车辆限界,电缆的最低点不在坐标轴原点,因此引入常数m0,对式(3)进行修正:
y=a[cosh(x/a)-1]x+m0
(4)
式中:m0为常数且为悬链线最低点到横坐标轴的距离。
P点的曲线斜率为tanγ,对式(4)进行求导,可得:
y′=tanγ=sinh(x/a)
(5)
弧长计算公式为:
(6)
将式(5)带入式(7),可得电缆长度L的方程为:
L=2asinh(x/a)
(7)
以轨道作为x轴,距离轨面的高度作为y轴,跨接电缆曲线轨迹示意如图2所示。

图2 跨接电缆曲线轨迹示意
2.3 中间车钩机械运动学对计算参数的影响
在列车实际运行中,会面临各种各样的工况,例如在过弯道时,车钩、贯通道外挡风、缓冲装置等部件的相对运动和振动等机械运动会使跨接电缆出现一定的拉伸和压缩。考虑到列车在实际运行中,2个车间车钩会产生相互运动,出现压缩或拉伸现象,因此会产生一定的误差,所以在跨接电缆计算过程中,需要考虑车钩机械运动学等因素,将这些可能影响的因素适当转化为数学参数,对模型计算公式进行修正。主要有以下2个参数[5]:车钩的拉伸(牵引时) 和压缩(制动时)量ΔL为30 mm;根据线路条件得知,线路最小半径为180 m,分析可得,此弯道内2辆车之间的距离的最大弯曲角α为12°。
以上参数是基于长沙某动车组实际运行线路进行选取。这2个参数对跨接电缆对应的安装结构和安装距离影响最大,直接影响电缆自由长度在实际运行工况下的变化。在计算过程中忽略由弯曲角α引起的电缆安装板在水平方向相对角度的变化。
综上所述,图2中的固定安装点P(x,y)的横坐标应修正为:
(8)
式中:ΔL为车钩最大伸缩量;α为车辆最大弯曲角;R为最大弯曲角时的线路曲率半径;T为电缆固定点到车体纵向中心线的距离。
结合以上分析,根据车辆参数求出动态固定点P(x0,y)以及tanγ,带入式(4)和式(5)中,得出:
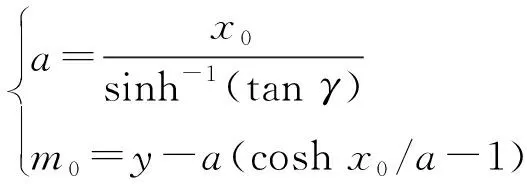
(9)
式中:a为常系数;γ为悬链线固定点P与y轴的角度;x0为固定点P的横坐标;m0为悬链线最低点与横坐标间的距离;L为悬链线长度。
3 MATLAB仿真计算结果验证
借助软件MATLAB仿真工具中的各运算模块来建立数学模型进行仿真运算,然后根据计算出的数据模拟出跨接跳线形状以及计算出跨接线缆长度。将本文的计算结果与实际结果进行对比,最终验证了基于悬链线方程的跨接电缆计算方法的可行性与准确性。
3.1 试验过程模拟计算结果分析
以某型动车组跨接为例,选取2节车厢之间的跨接电缆,计算设计跨接电缆的长度。 其跨接电缆设计输入参数如表1所示。

表1 跨接电缆设计输入参数
跨接电缆计算输出结果:L为跨接电缆长度;a为系数;m0为电缆中心线最低点到轨面的距离;em为电缆中心线最低点到轨面的距离与车辆限界的差值。
自然状态下(车钩无伸缩)的计算结果如表2所示。

表2 无拉伸(或压缩)时的输出参数
车钩拉伸达到最大时,根据式(8)对横坐标进行修正,即得到
(10)
得到x0为347,根据图3可得此时a为736。
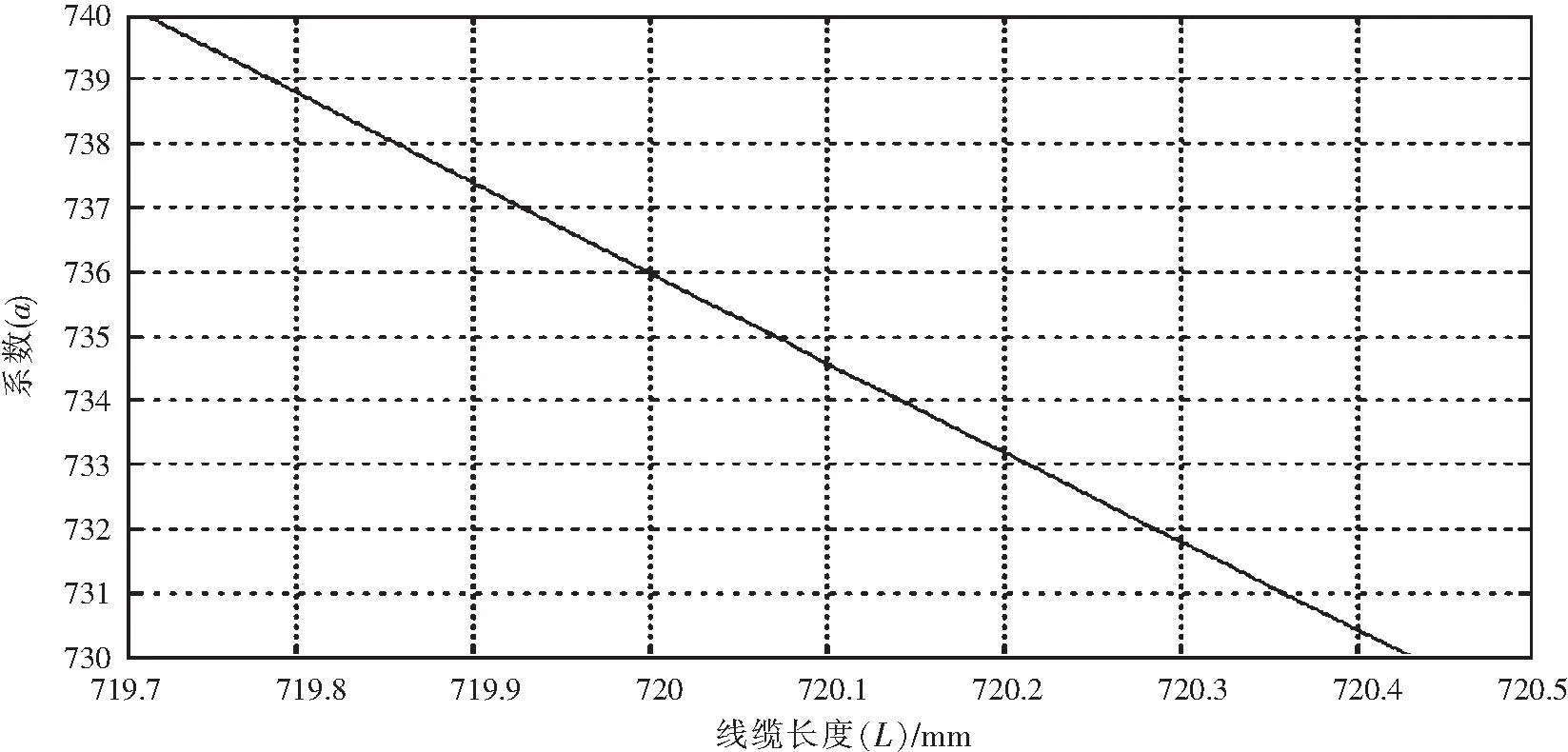
图3 车辆拉伸最大时的系数a与长度L曲线
车钩拉伸最大时,输出参数如表3所示。

表3 车钩拉伸最大时的输出参数
车钩压缩达到最大时,根据式(8)对横坐标进行补修正,即
(11)
得到x0为282,根据图4可得此时a为227.5。
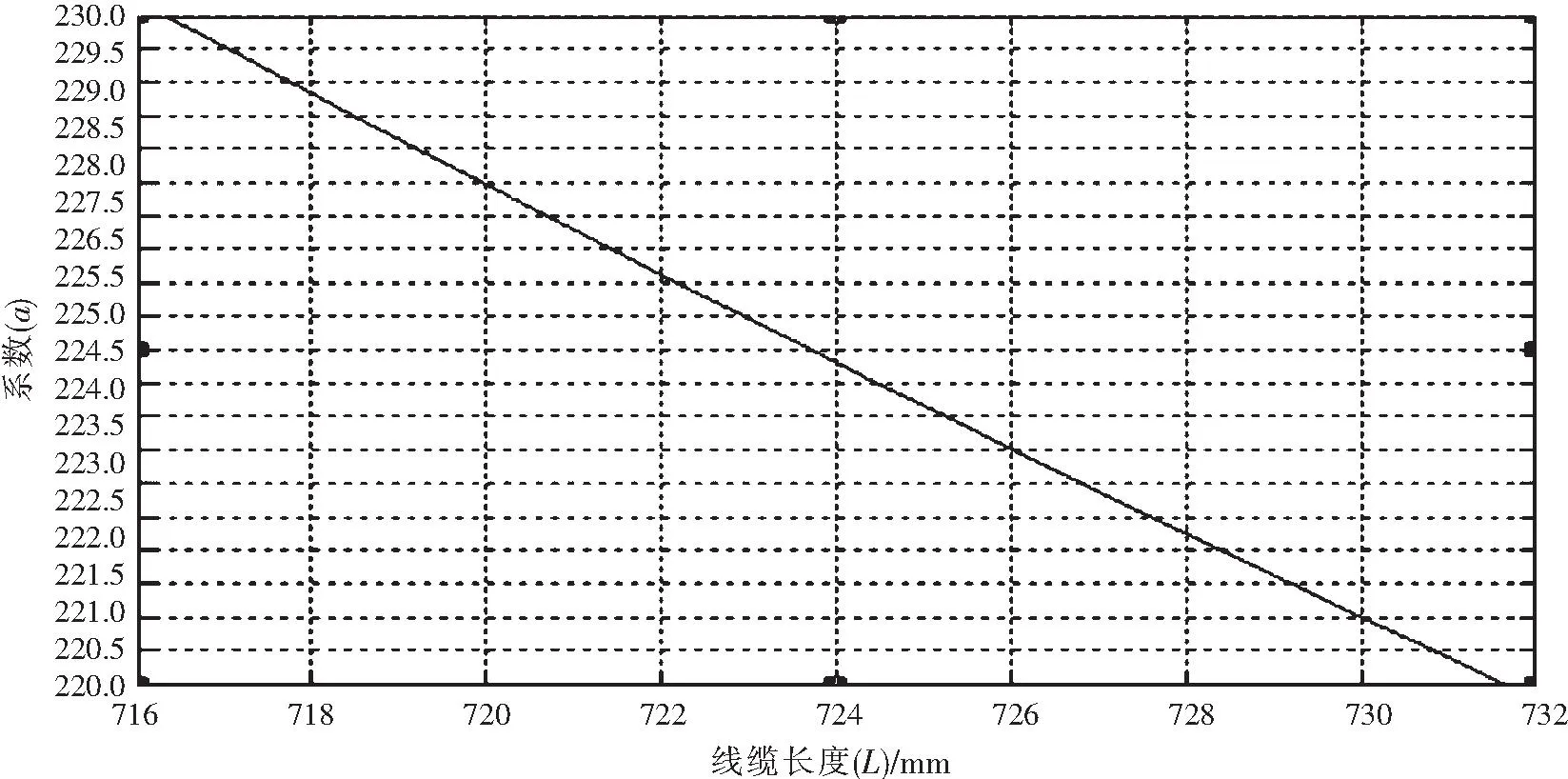
图4 车钩压缩最大时的系数a与长度L曲线
当车钩压缩最大时,输出参数如表4所示。

表4 车钩压缩最大时的输出参数
根据以上数据,可以模拟出自然状态下的跨接电缆形状,如图5所示。

图5 单根跨接电缆模拟自然状态
3.2 计算结果比较
将单根线缆自然状态、最大拉伸、最大压缩3种情况下的计算结果与实际结果相比较,如表5所示。

表5 计算结果与实际结果比较
从表5可以看到,计算长度与实际长度相差较小,自然状态下,电缆最低点距轨面高度为351 mm,而当车钩压缩最大时,线缆最低点距轨面高度为 302 mm,高于标准车钩压缩最大时的GB 146.1—2020《标准轨距铁路限界 第1部分:机车车辆限界》规定的限界244 mm,满足要求。
以上计算结果是基于单根线缆的数据计算所得,在实际过程中,主辅线同一竖直面可能会安装2根或多根线缆,模型如图6所示;下层线缆的数据如表5所示。按照同样的方法,上层计算出的结果如表6所示。

表6 上层电缆计算结果

图6 主辅线跨接电缆安装板
将同一竖直面上的2根线缆的结果与实际对比,可得表7。
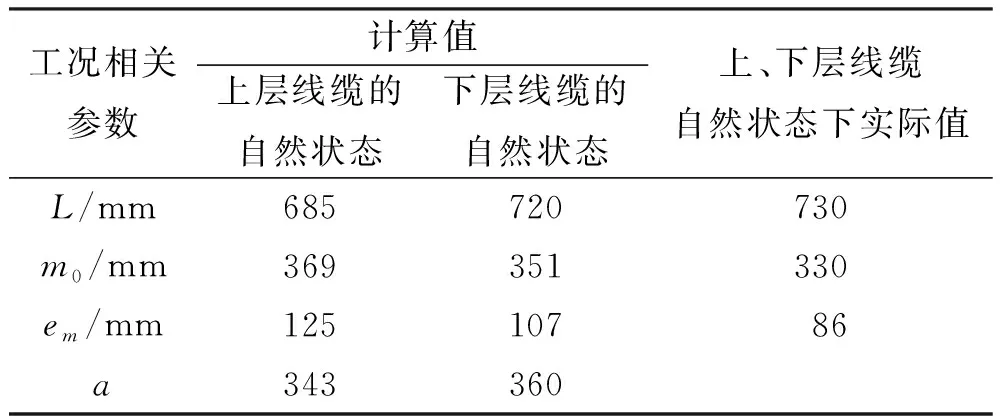
表7 计算结果与实际结果比较
根据表7线缆计算值,使用MATLAB仿真出线缆形状,如图7所示。

图7 主辅线跨接电缆仿真形状
根据模拟计算结果,可知同一竖直面上的2根线缆应该如图7所示,下层线缆较长,上层线缆较短。而在实际中,同一竖直平面的2根线缆一样长,这样会导致自然状态下造成线缆不合理的弯曲,运动过程中会产生摩擦,影响电缆的性能及寿命。
3.3 试验结果电缆弯曲半径的校核
电缆的最小弯曲半径(即曲率半径)是电缆本身的固有特性,为了保证电缆的正常使用,应保证基于悬链线设计和安装的跨接电缆满足最小弯曲半径大于电缆本身允许的最小弯曲半径。曲率半径公式为:
(12)
将式(5)代入式(9),可以得到悬链线方程的曲率半径公式为:
(13)
由上式可知,在x为0处,曲率半径最小,此时ρ为a,即电缆变形最大量在跨接电缆的最低点。从计算结果可知,当车钩的压缩量最大时跨接电缆最底部的弯曲半径为228 mm,而主辅线缆的直径为22 mm,按照要求电缆动态最小弯曲半径为220 mm,满足线缆应力要求,可见此处电缆受到的附加弯曲应力较小。
4 结束语
本文通过对电缆固定点附近受力的影响、车辆运动位置影响等进行分析,以MTALAB为仿真平台,建立了以悬链线方程为基础的跨接电缆长度计算模型,对本文中提出的仿真计算方法进行了验证,证明了模型对于计算车辆跨接电缆长度的可行性和准确性。
本文建立了跨接电缆的计算模型,并以某型动车跨接电缆为例,对模型计算结果进行验证,结果表明,此计算模型符合实际工程需求。

