基于空间逻辑回归模型的滑坡易发性评价

郑 雪，唐章英，宋 超

1.西南石油大学 地球科学与技术学院，四川 成都 610500；2.四川大学 华西公共卫生学院，四川 成都 610041

滑坡是中国山地丘陵地区发生频率最高的自然灾害之一，常造成多人伤亡和巨大的经济损失[1]。根据中国国土资源通报，2013年中国发生滑坡灾害数量占地质灾害总数量的63.9%，占比最大，并造成近500人死亡以及大约100亿元的直接经济损失(https：//www.mnr.gov.cn/)；同时，伴随着更密集的道路建设，过度放牧，农田耕作灌溉，矿山开采，城市向乡村扩张等人类活动对地质环境造成了一定程度的破坏[2]，地质环境变得越来越脆弱，再加上气候变化改变了全球极端降雨的频率和强度[3]，使得滑坡、崩塌、泥石流等一系列相关的地质灾害发生的概率大大增加。滑坡易发性制图是防灾减灾的一个重要工具，因为它可以指出滑坡的脆弱地区以便于我们有指向性的进行灾害防护。因此，选择合适的影响因素和研究方法来保证滑坡灾害制图和评估的准确性是减轻滑坡灾害损失的关键。

区域滑坡灾害易发性评价，有些研究也将其称为滑坡敏感性评价或是危险性区划，旨在区域尺度上(通常是一个较大的区域)根据当地的地理环境因素确定未来容易发生滑坡的地区并进行分级，量化不同因素对滑坡发生的影响，进而划分干预方式区别对待，这种方法已是主动有效预警滑坡并减轻灾害损失的重要手段之一[4]。一般来说，主要有基于机器学习算法的模型和统计方法的模型。基于机器学习的模型有支持向量机[5]、相关向量机[6]、人工神经网络[7]、灰色关联度[8]等。但是这类传统的机器学习方法往往需要大量的先验知识和假设，调参复杂，深度不足以完全提取潜在的滑坡特征[9]，不能合理地解释滑坡空间分布与滑坡风险因子之间的联系[10]。统计方法的模型包括逻辑回归[11]、贝叶斯空间统计[12]、频率比[13]、信息量[14]、确定系数法[15]等。现如今，逻辑回归模型、频率比模型、信息量模型、确定性系数模型已经有很多的学者进行了大量的研究并应用，这些方法比较容易快速实现，且原理较为简单。同时，也有一些文章将这几种模型进行组合并同单一模型进行对比，得到了相较于前人好一些的结果[16]。而贝叶斯空间统计模型由于考虑到数据的空间信息，与当前许多研究仅仅只利用数据的属性信息有较大区别，因为能够显著提升滑坡易发性预测的精度而得到推崇。

本文就是基于贝叶斯空间统计模型的分支——贝叶斯空间逻辑回归模型，使用当前主流的随机森林模型筛选风险因子后进行建模，对四川雅安芦山地区震后滑坡易发性进行分级并与普通未考虑空间结构信息的逻辑回归建模结果进行比较。

1 研究区域和数据

1.1 研究区概况

研究区大部分位于四川省雅安市内，跨雅安市市辖区、宝兴县、芦山县、名山县、荥经县、天全县，小部分位于成都市的大邑县和邛崃市，其地理覆盖范围接近29°87′-30°62′N 纬度和102°40′-103°30′E 经度，覆盖面积约4 888平方公里(图1)。该地区为亚热带湿润季风气候，夏季通常漫长、炎热且潮湿，冬季凉爽温和，全年降水量分布大致均匀，植被覆盖较为茂密。研究区地形自东南向西北，由平原、低丘陵转向高山，位于青藏高原和四川盆地之间的地形起伏很大的区域，有巨大的高差和陡峭的山坡。研究区大部分位于的雅安市是中国城市年降水量最高的城市之一，年均降雨量1 800毫米左右，有雨城之称(四川省公共气象服务网，https：//www.scggqx.com/)。

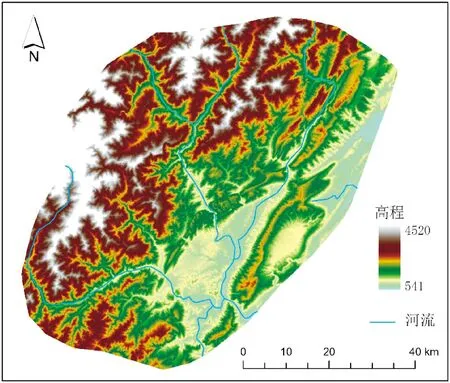
图1 研究区概况Fig.1 General situation

1.2 数据来源

研究使用的15 546个滑坡点清单来自于2013年4月20日中国庐山6.6级地震引发滑坡数据库。此数据库是基于之前不完整的数据库和补充遥感数据，包括地震后的高分辨率Rapid-Eye和ZY-3卫星图像，来建立的一个更详细、更客观、更完整的芦山事件的滑坡数据库[17]，并且在选定地区进行了现场调查来验证所得到的滑坡库存。

同时，本研究总共收集处理了16个影响滑坡发生的风险因素，分为地质地形 (高程、坡向、坡度、到断层的距离、岩性、地形、土地覆盖)、生态 (归一化植被指数、年平均降水量、地形湿度指数、到河流的距离)，以及社会经济 (到道路的距离、到居民点的距离)，地震相关因素(到震中的距离、地震烈度、峰值地面加速度)。具体来源如表1所示。

表1 风险因子数据汇总表Table 1 Summary of risk factor

2 风险因子的选取

2.1 共线性检查

为了使数据更容易解释和比较，对所有候选的风险因素进行了标准化。随后，在这些统计变量中，使用方差膨胀因子(VIF)结合斯皮尔曼相关系数进行筛选。VIF越大，多重共线性越严重，通常以VIF<10为阈值，再综合斯皮尔曼相关系数查看相关性>0.7的因子，删除两个相关性较高的因子的其中一个。最后，经过筛选和比较保留了除降水和地面峰值加速度之外的14个风险因子。

2.2 随机森林进一步筛选风险因子

由于将贡献率较低的风险因子纳入回归模型中将会影响其他相对重要的变量，所以使用随机森林这种流行且有效的方法进一步筛选对滑坡发生具有高度贡献的风险因子[18]。该方法不依赖于特定的模型假设，而是基于数据驱动的阈值来做出决策[19]。具体来说，就是要训练随机森林模型，再使用随机森林模型计算各个风险因子重要性得分。具有高重要性分数的风险因子是结果的驱动因素，它们的值对结果值有重大的影响。根据重要性得分对风险因子进行排序，选择排名靠前的11个因子作为滑坡是否发生的潜在预测因子(图2)。这些筛选后的风险因子能够构建更简单、更快速的预测模型。

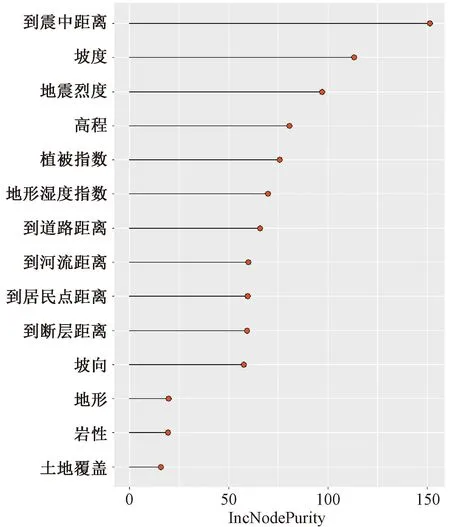
图2 随机森林筛选结果Fig.2 Random forest screening results

3 滑坡易发性评价模型及结果分析

3.1 逻辑回归模型

逻辑回归公式可用于根据各种风险因素对二元结果进行建模，对本研究来说体现为是否发生滑坡。它可以处理有多个自变量的情况，这对于模拟滑坡与各种风险因素之间的复杂关系非常重要[20]，已经在滑坡易发性评价领域得到了广泛的应用[21，22]。逻辑回归通过将滑坡事件的对数概率作为多个自变量的线性组合来对滑坡事件发生的概率进行建模，具体计算公式如下：

logit(P)=β0+β1X1+β2X2+…+βnXn

(1)

(2)

其中，P是滑坡事件发生的几率，logit(P)是滑坡事件发生的对数几率，β0是截距项，β1，β2，…，βn是要确定的回归系数，X1，X2，…，Xn是自变量。

3.2 贝叶斯空间逻辑回归模型

1970年，沃尔多·托布勒(Waldo Tobler)提出了地理学第一定律(空间自相关定律)：“一切事物都与其他事物相关，但进处的事物比远处的更相关[23]。”由于地理学第一定律的存在，使用空间回归模型，考虑数据的自相关性来对滑坡这种具有地理空间位置信息的数据进行建模是要比普通的回归模型更有道理的[24]。

空间逻辑回归是一种将逻辑回归与空间分析技术相结合的统计方法，它用于对二元因变量与一个或多个自变量之间的关系建模，同时考虑数据的属性信息和空间结构。在空间逻辑回归中，因变量是二元的，这意味着它只有两种可能的结果(滑坡或者不滑坡)，自变量可以是连续的或是分类的。简单来说，贝叶斯空间逻辑回归模型就是在普通逻辑回归模型之上考虑地理数据空间分布的结构信息，并采用贝叶斯统计的思想完成的适用于地理数据分析和预测的模型。该模型在考虑了数据的空间自相关性后，估计自变量的系数及其与因变量的关系，具体的计算公式如下：

Y=β0+β1X1+β2X2+…+βnXn+ρWY+ε

(3)

其中，Y是滑坡事件发生的对数几率，β0是截距项，β1，β2，…，βn是要确定的回归系数，X1，X2，…，Xn是自变量，ρ是空间自相关参数，W是n×n维的空间权重矩阵，其中n是滑坡单元的总数，该矩阵定义了滑坡单元之间的邻接关系。ρWY是由空间自相关引起的空间结构因素。ε是服从高斯分布的误差项。

3.3 评价结果及分析

在进行滑坡易发性评价之前，首先要将研究区划分为一个一个小的评价单元，以便于将风险指标进行收集与整理。目前主流的划分单元有两个：基于网格的单元和基于斜坡的单元，与基于网格的单元相比，斜坡单元可以贴切的反映研究区域的地形，更具有地貌意义[25]。本研究是采用改进后的曲率流域法将研究区划分为5 352个斜坡单元再进行滑坡易发性评价[26]。

为了避免过度拟合，把数据集划分为训练集(80%)和测试集(20%)，在训练集上训练逻辑回归和空间逻辑回归模型，并在测试集上评估其性能。再将模型得出的滑坡发生概率分别使用自然断点法进行分类，图3是逻辑回归输出的滑坡易发性图，图4是空间逻辑回归输出的结果。区别于传统的逻辑回归，空间逻辑回归还可以输出一个能够反应研究区空间自相关效应强弱的空间效应图(图5)，这是更具有空间自相关规律(平滑后的)的滑坡易发性风险趋势。可以观察到，空间效应图与空间逻辑回归输出的滑坡易发性图具有相似的空间格局，说明空间自相关效应提示了滑坡发生的风险。滑坡高易发区和极高易发区均集中在研究区中部，位于龙门山断裂带，沿盐井—五龙断裂、双石—大川断裂发育。这些滑坡易发区处在青藏高原与四川盆地之间高地势起伏区，海拔高的地区往往具有陡坡的特点，这会使土壤和岩石不稳定，更容易发生滑坡。起伏的地形会产生压力脊和凹陷，从而削弱土壤和岩石并使其更容易滑动。

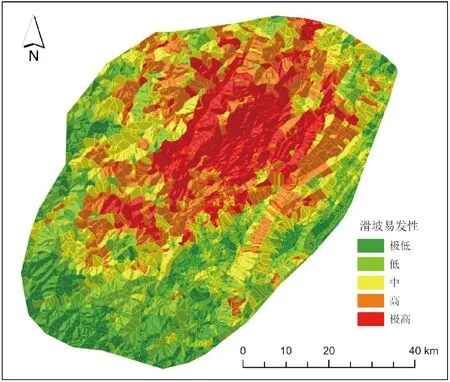
图3 逻辑回归易发性图Fig.3 Logistic regression susceptibility map

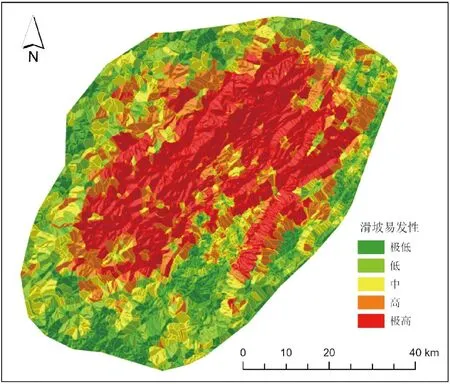
图4 空间逻辑回归易发性图Fig.4 Spatial logistic regression susceptibility map

图5 空间逻辑回归得出的空间效应图Fig.5 Spatial effect map obtained from spatial logistic regression

4 精度验证与讨论

本研究采用ROC曲线和混淆矩阵评估两个模型的性能。ROC曲线是二元分类模型性能的图形表示，它显示了灵敏度(真阳性率，TPR)和特异性(1-假阳性率，FPR)之间的权衡。通过测试每个可能的阈值并将每个结果绘制为曲线上的一个点来生成曲线，该曲线在 y 轴上绘制了 TPR，在 x 轴上绘制了 FPR(图6)。阈值是模型预测正类的概率，越靠近左上角的ROC曲线表示模型性能越好。ROC曲线下的面积 (AUC)是衡量模型在所有可能的分类阈值下的整体性能的指标。AUC的范围从 0到1，完美模型的AUC值为1，0.7～0.8是可以接受的识别能力，0.8～0.9是具有优秀的分类能力，模型的AUC值大于0.9表示模型具有杰出的分类识别能力[27]。混淆矩阵是显示分类模型的真正值、真负值、假正值和假负值的表格，它评估每个类的正确和错误分类实例的数量(表2)。

表2 混淆矩阵Table 2 Confusion matrix

图6 逻辑回归与空间逻辑回归ROC曲线图Fig.6 ROC curves of logistic regression and spatial logistic regression

如图6所示，空间逻辑回归模型的AUC值相较于传统的逻辑回归模型提升了近14%，大于了0.9，表示此模型具有杰出的分类识别能力。对比来看，空间逻辑回归模型的ROC曲线也更靠近左上角，说明对于存在空间自相关性的滑坡数据，空间逻辑回归模型在模型的预测效果方面显著优于传统的逻辑回归模型。结合混淆矩阵，空间逻辑回归的预测准确率为84.9%，在传统逻辑回归的基础上提升了11.5%，单独比较阳性(滑坡)预测正确率和阴性(非滑坡)预测正确率也分别提升了14.3%和9.8%。为了更直观的进行比较，我们利用源数据生成了实际滑坡点密度图(图7)，空间逻辑回归的预测结果(图4)与其高度一致，而传统逻辑回归在研究区东北边缘将没有发生滑坡的区域预测为高和极高易发性，在研究区西南有滑坡发生的区域预测为低和极低易发性。出现这种差异的原因还是在于有没有考虑空间自相关这个不可忽视的风险因子，空间自相关效应(图5)会导致传统的回归模型高估或低估某些区域的滑坡易发性。因为邻近的区域往往具有相似的特征，如果这些特征与滑坡的发生相关联，则模型可能预测附近区域也容易发生滑坡，即使它们在传统回归模型的预测中并不容易发生滑坡。

图7 实际滑坡点密度图Fig.7 Actual landslide point density map

5 结论

总的来说，空间逻辑回归模型具有在斜坡单元水平上定义的空间潜在效应，允许评估模型中的影响因子仍然无法解释的空间影响，大大提高了传统逻辑回归模型的性能和预测精度，易于绘制出更准确的滑坡易发性地图，从而帮助政府确定高滑坡风险区域，并因地制宜的采取适当措施降低风险，这有助于保护人民的生命和财产，减少滑坡对社会的整体影响。