中国省域科技创新水平评价
李国柱,黄琪骏
1.河北地质大学 经济学院,河北 石家庄 050031;2.中央财经大学 保险学院,北京 100081
0 引言
社会发展的经验表明,科技的革新能改变世界的发展水平,对国家的发展前景具有深远的影响。回首过去,中国凭借“四大发明”引领了世界的发展。通过不断的努力,中国的综合科技水平持续得到改善,并且在许多领域中领先世界其他国家。在农业科学技术、国防军事科学、生物医学科学技术、信息技术等方面创造了良好成绩。
随着经济社会的飞速发展,愈发让我们意识到科技创新[1]是中国共产党执政兴国的重要方略。2015年10月,“十三五”规划基于中国发展前景,针对性地提出“创新、协调、绿色、开放、共享”的五大发展理念。在五大发展理念中,创新发展强调要把创新置于中国总体发展核心地位,持续促进科技、理论和制度等的全方面的创新。2017年10月,党的十九大报告指出,中国经济发展方向得到转变,已经从之前的高速增长转变为高质量发展。创新是使国家能够高质量发展、前进的动力,需要尽可能利用其在经济高质量发展过程中的带头作用。创新是促进发展的中坚力量,科技创新对经济发展的重要性显著增强是经济高质量发展的特征之一。
科技从来没有像今天这样对一个国家的未来起着重要作用。推进科技创新的发展,完善中国创新体系,加快建设中国成为科技强国[2]。这不仅是党中央针对世界科学技术的发展和竞争以及综合国家实力竞争的发展趋势和客观规律做出的科学性判断,也是吸取中国社会发展的历史经验和教训得出的结论。新时代的到来,代表着近代以来饱受苦难的中华民族迎来了从站起来、富起来到强起来的绝对飞跃,这必须得到科技创新的坚定支持,在不断提高自主创新能力的基础上向前发展。因此,探索全国31个省市(限于数据的可得性,未包括香港、 澳门特别行政区和台湾省)科技创新发展情况,有利于了解中国各地区科技创新发展水平,反映各省市经济高质量发展状况。
1 数据来源与变量选取
1.1 数据来源
文章对全国31个省市科技创新的发展水平进行评价。利用到的相关科技创新数据主要来源于《中国统计年鉴2020》。
1.2 变量选取
参考ZHANG Y et al.[3]构建的科技系统,结合2019年中国科技创新数据,选择8个正向指标,分别是规模以上工业企业的R&D经费、规模以上工业企业的R&D项目数、地方科学技术投入资金、授权专利数、技术市场成交额、产品质量合格率、普通高等学校正高级专任教师和普通高等学校数目。上述8个指标均为正项指标,当其数值越大时,说明该地区科技越发达。
2 主成分分析
2.1 主成分分析概念
主成分分析方法最初由皮尔森将非随机变量进行代入,然后由霍特林对该方法进行了改进,使其同样适用于随机变量。一般情况下使用离差平方和或者方差来衡量变量所包含信息的多少。主成分分析:利用降维的想法将原始变量组合成互不相干的新变量,进而依据现实要求,从中提取出少量的总变量,以达到可以充分体现原始变量信息的目的[4]。
经过线性组合,将初始的P个指标变量重新组合成n个综合指标。用选取的第一个线性组合F1的方差Var(F1)来说明信息量的多少,方差越大,代表F1所包罗的信息就越多。因此F1作为第一主成分,在选取的全部线性组合中,它的方差是最大的。当第一主成分F1未能充分表示初始P个指标变量信息时,需要选择第二个线性组合F2,为达到能有效表示初始信息的目的,已经存在于F1中信息此时不必再呈现于F2中。F1与F2的协方差为零,这时选取的第二个线性组合F2被称为第二主成分。根据上述步骤,在需要的情况下,继续选取第三、第四,……,第P个主成分[5]。
2.2 主成分确定
利用SPSS软件,利用主成分分析方法对原始指标进行降维,从而提取主成分。采用极差法对初始数据进行标准化处理,再对初始数据的样本进行充足性检验,结果见表1。

表1 KMO和Bartlett的检验Table 1 KMO and Bartlett′s test
根据表1,KMO值为0.730>0.5,这说明给定的样本充足。Bartlett的球形度检验Sig.值为0.000<0.05,可以拒绝Bartlett的球形度检验的零假设,说明原始变量间具有相关性,KMO值与Bartlett的球形度检验均说明该原始数据可以进行因子分析。
公因子方差结果见表2,呈现了在本次分析过程中,从各个初始变量中所提取到的信息情况,信息提取方法为主成分分析,提取度均在0.7以上,说明主成分涵盖每个初始变量较多的信息。
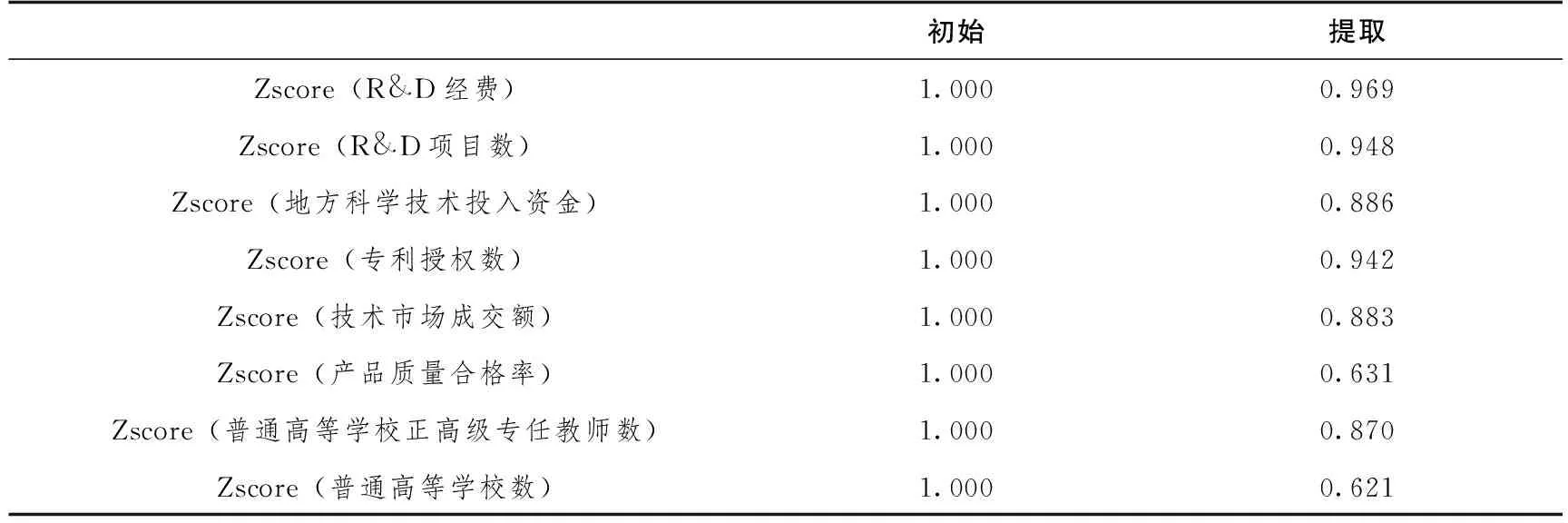
表2 公因子方差Table 2 Common factor variance
表3解释的总方差说明了各主成分解释初始变量总方差的状况。依据累计贡献率靠近85%,选取2个主成分,将8个变量转化为2个新指标,起到了降维的作用。

表3 解释的总方差Table 3 The total variance explained
未旋转的因子载荷见表4,结果显示提取2个主成分。R&D经费、R&D项目数、地方科学技术投入资金、专利授权数、产品质量合格率、普通高等学校正高级专任教师数以及普通高等学校数,在成分1上具有较高载荷,表明成分1能够大致表示上述指标的信息情况。技术市场成交额在成分2上拥有较高载荷,表明成分2能够大致表示技术市场成交额的信息。因而表明提取两个主成分能够大体代表原本指标信息。
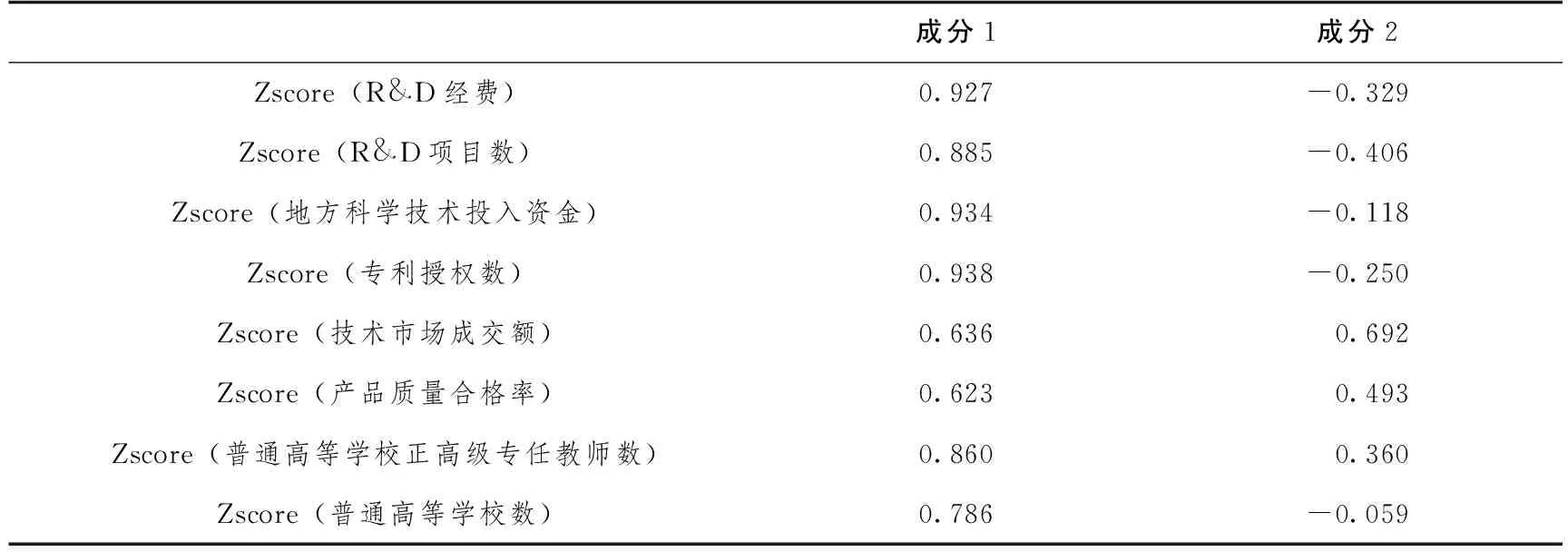
表4 成分矩阵aTable 4 Component matrix a
2.3 主成分得分
成分得分系数矩阵见表5。

表5 成分得分系数矩阵Table 5 Coefficient matrix of component scores
主成分得分情况见表6,其中Y1与Y2分别代表第一主成分得分与第二主成分得分,Y代表主成分综合得分。对主成分综合得分Y进行排名,主成分综合得分在前5名,即地区科技创新发展水平在前5名的分别是广东、北京、江苏、浙江、山东,说明2019年这些地区科技创新水平较高,可能是北京作为中国首都,以及腾讯、阿里巴巴等高科技公司在广东、浙江的原因。主成分综合得分在后5名,即地区科技创新发展水平在后5名的分别是新疆、海南、西藏、宁夏与青海,说明2019年这5个地区科技创新水平较低,可能是地处偏僻、经济社会发展较缓慢的原因。

表6 主成分得分Table 6 Principal component scores
3 有序聚类分析
3.1 有序聚类概念
通常的聚类分析,各个样本之间是平等的,在进行聚类时,是将所有样本混合在一起,以距离或相似系数的标准来对样本进行分类[6]。有序聚类法作为一种常用的聚类分析方法,将n个样本根据某种条件(时间、底层深度等)进行排序,只有次序相邻的样本才可以聚为同一类。
本质上,有序样本的分类是在样本中寻找n个划分点,并且使用寻找的n个划分点将以某种顺序排列的样本分段,并且将划分后的每个片段看作不同类别。当划分点在不同位置处被获取时,能够获得完全不同的划分结果。为了确保最佳划分方法,首先必须使划分后的各个段内样本之间的差异达到最小化,同时需要与不同段的样本之间达到差异最大化。因此有序聚类法又称为最优分割法[7]。
3.2 结果分析
利用R软件,对全国31个省市科技创新水平的主成分综合得分降序排名,进而对其进行有序聚类分析,有序聚类结果见表7。

表7 有序聚类表Table 7 Ordered clustering table
由表7可知,全国31个省市通过有序聚类可聚4类。第一类包括排名为19~31的地区,即黑龙江、云南、广西、贵州、甘肃、山西、内蒙古、吉林、新疆、海南、西藏、宁夏和青海,这些地区地理位置偏僻,经济发展水平较低,科学创新发展情况较差。第二类包括排名为9~18的地区,即湖南、安徽、河南、陕西、辽宁、福建、江西、河北、天津和重庆,上述省市大部分属于华北和华中地区,经济与科技创新发展情况一般。第三类包括排名为4~8的地区,即浙江、山东、上海、湖北和四川,这些地区经济发展状况相对较好,科技创新实力较强。第四类包括排名为1~3的地区,即广东、北京和江苏,这3个地区经济社会发展情况很好,北京作为中国首都,聚集众多高新科技,广东、江苏具有良好的地理优势、经济高速发展的条件,科技创新发展情况在全国最强。
4 结论与建议
4.1 结论
(1)2019年全国31个省市的科技创新发展数据适合主成分分析,可以提取2个主成分。计算主成分得分,并对主成分综合得分Y进行排名。排名依次是:广东、北京、江苏、浙江、山东、上海、湖北、四川、湖南、安徽、河南、陕西、辽宁、福建、江西、河北、天津、重庆、黑龙江、云南、广西、贵州、甘肃、山西、内蒙古、吉林、新疆、海南、西藏、宁夏及青海。
(2)对全国31个省市主成分综合得分排名进行降序排列后,对排名进行有序聚类,能聚4类。第一类包括排名为19~31的地区,第二类包括排名为9~18的地区,第三类包括排名为4~8的地区,第四类包括排名为1~3的地区。
4.2 建议
从结果中可以看出广东、北京和江苏,这3个地区科技创新发展状况最好,聚为一类。三者经济、科技等发展水平在全国范围内均属于领先地位,社会发展势头好。黑龙江、云南、广西、贵州、甘肃、山西、内蒙古、吉林、新疆、海南、西藏、宁夏和青海,由于地域因素,经济发展水平较低,科学创新发展情况较差,与广东、北京及江苏比较,经济社会发展情况较差。针对上述分析,现提出以下几点建议。
(1)缩小地区发展差距。研究结果表明,中国各地区间的发展存在一定的差距。其中金融、城镇化以及对外开放作为影响地区经济差距的主导力量[8],经济发展与科技创新关系密切。北上广深等大城市经济社会发展情况良好,科技创新发展实力较强,相比之下,中国偏远地区,云南、广西和甘肃等省市经济发展情况差,科技创新水平较低。缩小地区差距对全国科技创新的整体发展存在重要意义。
(2)坚持“引进来”的发展战略[9]。科技是第一生产力,科技人才是科学技术发展的根本。深究贫困地区中经济水平相对较高的省市,大部分存在政府支出来聘请外部科技人员的现象。这些人才一般具有丰富的经验,能够通过科学技术繁荣农业,拥有新的科学技术并且能将其付诸实践。但是,一般贫困地区地处偏僻,而且在恶劣气候和生活条件下,吸引人才是一项重要而又艰巨的项目工程。在发展的过程中,中国也应该注意东西部地区的结合,借鉴东部地区发展的经验,来促进西部地区的高效发展,加快缩小东西发展差距[10]。遵循共同富裕、互惠互利的发展原则,推动中国东西部地区之间的高效协调发展。

