基于产状Fisher分布的岩石节理最小样本容量确定方法
杨梓枫,夏华宗,杜玉芳,王晓明,3
1.河北地质大学 城市地质与工程学院,河北 石家庄 050031;2.河北地矿建设工程集团有限责任公司,河北 石家庄 050000;3.河北省地下人工环境智慧开发与管控技术创新中心,河北 石家庄 050031
0 引言
节理是岩体中普遍发育的一种结构面,这些结构面将完整岩体切割成大小不等、形状各异的岩石块体,而且节理通常强度低、易变形,同时能够为地下水提供存储空间和运移通道,对岩体的完整性、力学特性、渗流特性及稳定性起着控制作用。节理产状是影响岩体结构及其工程性质的关键参数之一,其平均值及离散性对边坡、地下洞室等工程岩体的稳定性及可靠性具有显著影响[1,2]。因此,准确计算节理的平均产状及其离散性对掌握岩体的工程特性进而开展工程岩体的评价、设计及施工具有重要意义。
节理平均产状的准确性受样本容量(即采样数量)和离散性的影响,产状离散性越大,则节理的采样数量应越大,反之亦然。为保证统计结果的准确性,节理样本应不少于某一数量,该数量即为最小样本容量。在实际工程中,受采样条件的限制,如节理露头较少或测量困难而造成采样数量较少,平均产状的统计准确性势必会受到影响。因此,确定节理的最小样本容量对于节理统计分析具有现实意义。
岩体中的节理往往具有一定的方向性,通常会沿2~5个优势方向发育,产状相近的节理应划分为同一组。节理的产状一般用倾向(或走向)和倾角表示,同一组节理的产状通常服从一定的分布形式。常见的节理分布类型包括Fisher分布、Bingham分布和双正态分布等[3-6]。其中,Fisher分布由于仅包含1个参数且为可积分函数便于实现Monte Carlo模拟,得到了广泛应用[7-12]。此外,一些研究表明,实测节理产状能够较好地拟合Fisher分布[13,14]。由于节理发育的随机性和离散性,在工程实践中通常将节理进行分组统计来确定每组节理的平均产状[15-17]。
基于节理产状服从Fisher分布,本文探讨产状离散性对节理采样数量的影响。通过Monte Carlo随机模拟技术产生具有不同离散性的产状随机数,在保证准确性的条件下确定节理的最小样本容量,并建立最小样本容量与产状离散性的经验关系,最后通过算例验证其适用性。
1 Fisher分布及产状离散性
该分布于1953年由Fisher提出,是一种将节理产状视为球面上关于平均产状对称的分布形式[3]。Fisher分布的概率密度函数为:
(1a)
(1b)
式中,θ′和φ′分别是当把坐标系z轴旋转至节理的平均矢量方向(θm,φm)后在新坐标系中的方向角;参数κ反映了节理产状分布的离散性或集中程度,κ越大表明节理的产状围绕平均产状越集中,即离散性小。如果κ=0,则Fisher分布转化为球面上的均匀分布。均质岩体中的构造节理产状通常较为集中,具有较大的κ值;而非均质岩体中的节理产状往往具有较大的离散性,其κ值通常较小。κ可按下式计算[3]:
(2)
式中,N为节理的数量;rN为节理的和向量,其方向即为节理的平均产状,其计算过程将在2.2节中详述。Watson的研究认为当κ>3时,公式(2)的计算结果具有足够精度[18]。众多研究表明[10-12],同一组节理的κ一般大于3,因此公式(2)具有较好的适用性。
2 研究方法
2.1 Fisher分布产状的随机生成
节理的方向是以其单位法向量表示的,一般取指向上方的法向量。在直角坐标系中(图1),假设OP为某节理的单位法向量,点N为P点在xOy平面上的垂直投影,θ为OP与z轴正方向的夹角,φ为x轴正方向沿逆时针方向与ON的夹角。
Fisher分布是当把z轴旋转至节理的平均矢量方向(θm,φm)之后的形式,此时它的两个变量θ′和φ′是独立的,其概率密度函数见公式(1)。其中φ′服从(0,2π)之间的均匀分布,可直接利用公式(3)产生,u为(0,1)范围内的均匀分布随机数。
φ′=2πu
(3)
θ′的密度函数是一个可积分函数,其累计分布函数为:
(4)
这样可利用逆变换法产生Fisher分布的随机数,即:
(5)
得到:
(6)
如果称旋转前(z轴铅直向上)的坐标系为旧坐标系,它的变量为(φ,θ);称旋转后(z轴与节理的平均矢量一致)的坐标系为新坐标系,它的变量为(φ′,θ′),则两个坐标系的变化关系为[7,9]:
式中:(l,m,n)和(l′,m′,n′)分别为对应(φ,θ)和(φ′,θ′)的方向余弦。l,m,n分别为:
(8)
地质学中,节理的方向是用倾向和倾角(α,β)表示的,而非(φ,θ)。如果采用图3中的坐标系,(α,β)和(φ,θ)的关系可以用下式计算:
(9)
综合上述分析,产生一组N个Fisher分布的随机节理产状的过程如图2所示。
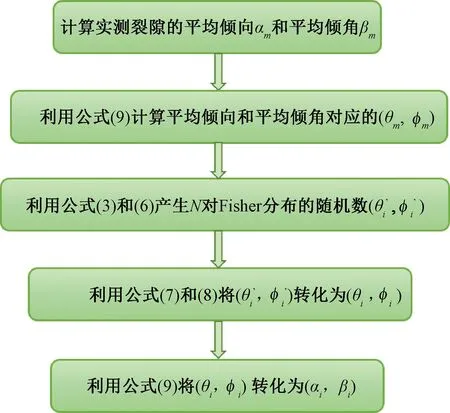
图2 Fisher分布随机节理产状的产生流程Fig.2 Generation flowchart of random joint orientation obeying Fisher distribution
2.2 节理平均产状计算
节理平均产状是指节理组中每一条节理面的单位法向量之和所在的方向。假设一组节理包含N条节理,每一条节理的倾向和倾角分别为φi和θi,通过公式(8)可以得到每条节理的单位法向量。由于节理产状的离散性,节理产状的分布范围有时较大,当采用上半球赤平极射投影时可能出现“超越上半球投影的产状”(OEBEUHP)[9,13]。图3为200个随机产生的服从Fisher分布的节理产状,其平均产状为45°∠60°,κ=10,其中11个节理极点为OEBEUHP。
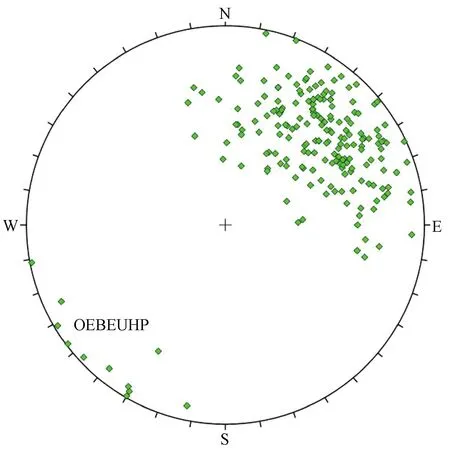
图3 平均产状为45°∠60°的节理产状极点图(κ=10)Fig.3 Pole diagram of joint orientations with mean orientation of 45°∠60°(κ=10)
由于存在OEBEUHP,同一组节理向上的法向量之间的夹角可能大于90°,所以在计算节理平均产状时,不能将节理的法向量ni简单相加,应考虑采用ni还是-ni。郑俊等提出了一种识别和调整OEBEUHP的策略,通过计算ni与合向量rN的夹角来识别OEBEUHP,并用-ni重新计算rN[9,13]。实际上,初始rN的计算已经存在由OEBEUHP引起的问题,因此这种策略需要适当调整。本文在此基础上,提出了一种计算rN的修正方法,具体过程见图4。根据得到的rN,可利用公式(8)和(9)将其转换为节理的平均产状。节理产状的随机生成和平均产状的计算均通过Python程序实现。
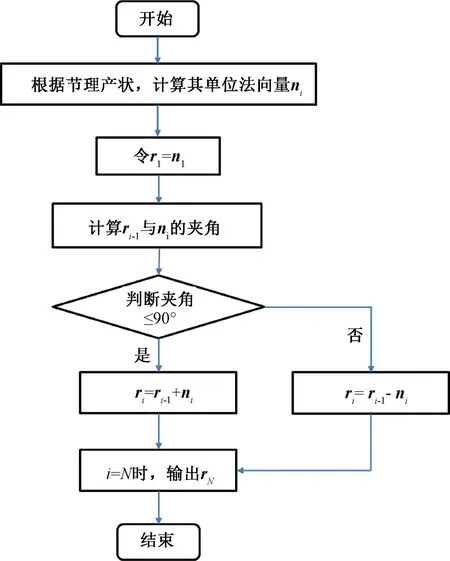
图4 节理和向量rN的计算过程Fig.4 Calculation process of joint and vector rN
3 最小节理采样数量的确定
由于节理产状的离散性,节理平均产状的计算结果受样本大小的影响。产状离散性越大,即κ值越小,节理的样本容量应越大才能保证平均产状计算的准确性。本文以平均产状为45°∠60°的节理为例,通过随机生成不同数量、不同κ值的Fisher分布产状来研究样本容量对平均产状计算准确性的影响,κ值分别取5,10,15,20,25,30,35,40,45,50,55,60,70,80,90和100。对于每一个κ值,共进行1 000次抽样,样本容量为ns。图5绘制了一次随机实现时不同κ值的节理极点分布图,样本容量ns为250。
若每次抽样的平均产状与45°∠60°的夹角小于5°,则认为满足准确性要求。将满足以上要求的抽样次数记为np,那么准确率p可以定义为:
(10)
当κ≤40时,每次抽样的样本容量ns为5的倍数;当κ>40时,ns为自然数。
图6反映了不同κ值时样本大小对平均产状准确率的影响。样本容量对平均产状的统计准确性影响显著,样本容量越大,平均产状的统计准确率越高;产状离散性(即κ值)对统计准确率也有明显影响,离散性越大即κ值越小,达到一定准确率所需的样本数越多。一般情况下,准确率p为0.95可满足工程要求,因此将p=0.95对应的样本容量定义为最小样本容量。当样本大小超过最小样本容量时,可以保证产状的统计准确率不低于0.95。图7为具有不同κ值的节理产状所应满足的最小样本容量ns,min,可以看出,ns,min随着κ值的增大迅速减小,当κ值达到40以后,ns,min的变化很小且趋于水平。为方便在工程实践中确定节理的最小样本容量,采用反比例函数(公式(11))对ns,min和κ值的关系进行拟合,得到了图7中的拟合曲线。公式(11)的确定系数R2为0.994,表明该式能准确反映ns,min与κ值的反比例关系,可用于确定节理的最小样本容量。
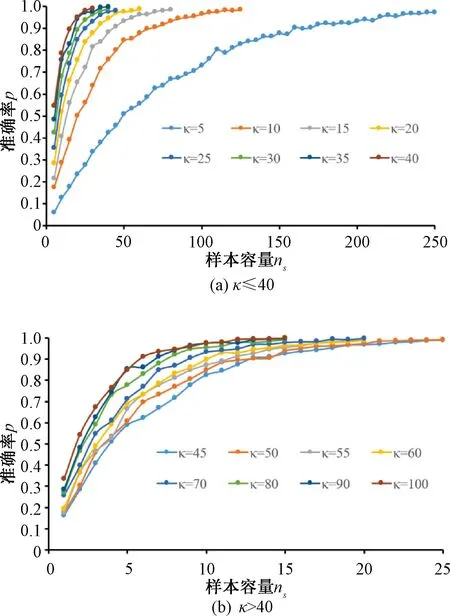
图6 不同κ值时样本容量对统计准确率的影响Fig.6 Effect of sample size on statistical accuracy with different κ values
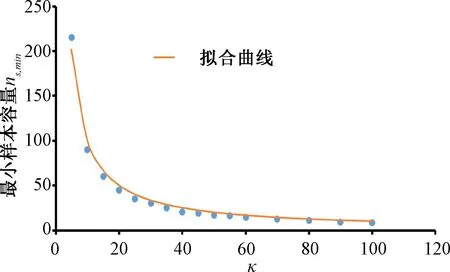
图7 不同κ值对应的最小样本容量Fig.7 Minimum sample size corresponding to different κ values
(11)
实际上,在对节理产状进行采样之前无法预知节理组的κ值。但随着采样过程的进行,会得到越来越多的产状数据,可以利用这些数据对κ值进行估算,从而判断最终的采样数量ns是否满足公式(11)的要求。如果ns不小于ns,min,则采样数量满足要求,平均产状的准确率能够得到保障。本文的研究基于产状服从Fisher分布,实际岩体中大多数构造节理均成组发育且服从Fisher分布,因此公式(11)对构造节理具有较好的适用性。对于孤立的随机节理,其发育没有规律性,不适合采用公式(11)进行计算。
4 验证算例
为验证公式(11)的适用性,对三峡工程地下厂房的上游边墙和乌东德水电站平洞PD5-2节理产状进行了抽样统计分析。三峡水电站是世界上最大的水利枢纽之一,位于中国湖北省宜昌市夷陵区。地下电站位于长江右岸白岩尖山体内,主厂房洞室为圆拱直墙型,全长 311.3 m,轴线走向 223.5°,最大跨度 32.6 m,最大高度 87.3 m。厂房围岩为坚硬的花岗岩,岩体完整~较完整,整体稳定性较好。地下电站厂房洞室的开挖揭露了708条节理,分组后的节理极点分布情况见图8,每组节理产状的统计参数见表1。乌东德水电站平洞PD5-2位于金沙江乌东德坝址左岸850 m高程,为顺江支洞。平洞洞形为城门洞形,断面尺寸约2 m×2 m。本平洞共揭露节理354条,分组后的节理极点分布情况见图9,每组节理产状的统计参数见表2。

表1 三峡地下厂房上游边墙节理产状统计结果Table 1 Statistical results of the orientation of joints in the upstream side wall of the Three Gorges underground powerhouse
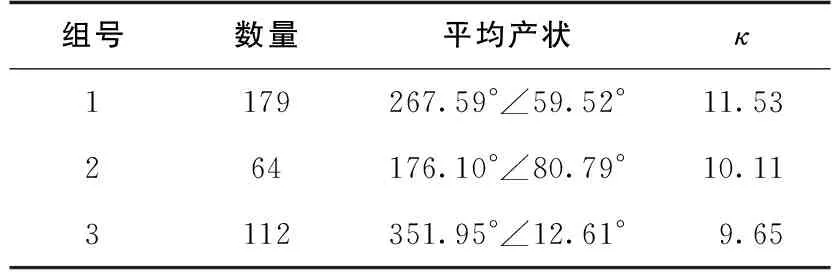
表2 乌东德水电站平洞PD5-2节理产状统计结果Table 2 Statistical results of the orientation of joints in the adit PD5-2 of the Wudongde hydropower station
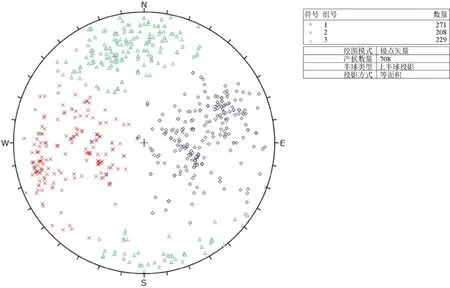
图8 三峡地下厂房上游边墙节理极点分布图Fig.8 Distribution diagram of joint poles in the upstream side wall of the Three Gorges underground powerhouse
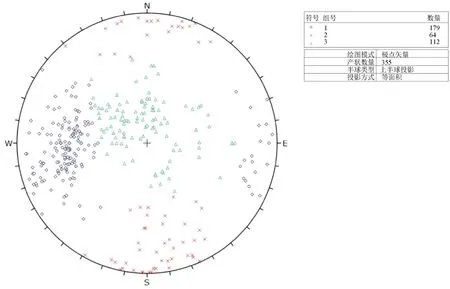
图9 乌东德水电站平洞PD5-2节理极点分布图Fig.9 Distribution diagram of joint poles in the adit PD5-2 of the Wudongde hydropower station
根据公式(11),计算出三峡地下厂房上游边墙每组节理的最小样本容量应达到97、97和105。接下来,对每组节理产状进行模拟抽样,抽样次数均为1 000次,样本大小为最小样本容量。最后利用公式(10)计算抽样结果的准确率。经程序计算,每组节理平均产状的准确率分别为0.988、0.992和0.994,均满足准确率要求。该研究区每组节理的采样数量均大于相应的最小样本容量,满足采样要求。因此,三峡工程地下厂房的上游边墙的节理产状具有统计学意义。
根据公式(11),计算得到乌东德水电站平洞PD5-2每组节理的最小样本容量应达到87、100和104。假设每组节理采样数分别为80、90和95,未达到相应组别的最小样本容量。利用公式(10),计算出每组抽样结果的准确率分别为0.955、0.948和0.946。结果表明,除第一组采样能达到准确率以外,其余两组未能满足准确率要求。抽样过程具有一定的随机性和偶然性,在抽样数量不足时,仍有较小可能达到准确率,但是为保证抽样结果具有较高的可信度,节理抽样应达到最小样本容量的要求。本节通过正反两个算例验证了公式(11)的可靠性,表明节理最小样本容量ns,min与κ值的经验关系适用于确定节理产状的最小样本容量。
5 结论
本文基于节理产状服从Fisher分布,实现了节理产状的随机生成。为解决“超越上半球投影的产状”(OEBEUHP)引起平均产状计算不准确的问题,提出了一种计算平均产状的修正方法。在此基础上,随机生成不同数量、不同离散性(κ值)的Fisher分布产状来研究节理样本容量对平均产状准确性的影响,并建立了最小样本容量与κ值的经验关系。研究结果表明:节理样本容量对平均产状的统计准确性影响显著,样本容量越大,平均产状的统计准确率越高;产状离散性对统计准确率也有明显影响,离散性越大即κ值越小,达到一定准确率所需的样本数越多。为保证平均产状的统计准确率不低于0.95,节理的最小样本容量随着Fisher分布常数κ值的增大迅速减小;二者之间具有明显的反比例关系,反比例系数为1 007.23,经验公式的确定系数为0.994。对三峡地下厂房上游边墙和乌东德水电站平洞PD5-2的节理统计分析从正反两方面验证了本文方法的适用性,节理采样具有一定的随机性,在满足最小样本容量的条件下,产状统计分析结果具有较高的可靠性。本文提出的方法适用于确定节理产状的最小采样数量,判断节理的采样数量是否具有统计意义,能有效指导节理的采样工作。

