环形丁腈橡胶件静刚度的有限元模拟

范宗瑞,张 健,霍肇波,姜雨霆,郝文龙

(1.中国船舶集团有限公司第七○三研究所,哈尔滨 150078;2.南京航空航天大学机电学院,南京 210016)

0 引 言

橡胶作为一种高分子非线性超弹性材料,广泛应用于承载结构轴承、密封件、吸振垫、连接器和轮胎中,已成为现代工业的重要原材料[1]。橡胶具有很强的可变形能力和不可压缩性。为了能在应用中合理设计橡胶零件的结构尺寸,需了解其静刚度特性,为此首先需要获得橡胶材料的超弹性本构模型参数,在其基础上利用有限元方法获得零件的数学模型,从而对静刚度特性进行仿真。许多学者对橡胶的超弹性本构模型进行了研究,例如:LUO[2]提出了一种根据试验数据预测橡胶时变响应与蠕变、松弛等行为的时变超弹性本构模型;李雪冰等[3]提出了一种改进的Yeoh超弹性本构模型,并且通过试验证明了该模型可以模拟橡胶在大应变状态下的应力、应变关系;刘晓东等[4]利用试验得到的应力、应变数据识别参数,建立了硅橡胶的超弹性Mooney模型;WANG等[5]利用Mooney-Rivlin模型和Ogden模型对橡胶支座进行了静态特性仿真分析。橡胶的自身结构会对其静态特性产生影响。陈茜[6]提出了基于不完全信息的材料力学参数识别方法,并基于此方法得到三阶Ogden超弹性本构系数,并用该模型分析了缩颈量对橡胶衬套静态特性的影响;于永杰[7]利用Mooney-Rivlin模型对4种不同结构类型的橡胶悬置进行静态仿真分析;邱跃统等[8]在ABAQUS软件中采用Mooney-Rivlin超弹性本构模型对橡胶进行材料属性定义,计算分析了楔块结构数量及孔结构形式对橡胶联轴器静态特性的影响。外界环境因素也会对橡胶材料的静态特性产生影响。衣晨阳[9]使用不同温度下的静态拉伸试验数据拟合出不同温度下的Yeoh本构模型参数,并使用该参数定义材料属性,通过有限元仿真分析了不同温度下橡胶减振器的静态特性。

丁腈橡胶作为一种常见的橡胶材料,制成的环形结构件在机械传动装置的隔振方面有着重要的用途。但目前关于环形丁腈橡胶件的静态特性,尤其是静刚度受自身结构尺寸及温度影响的报道相对较少。相比于矩形结构件,环形结构件的结构复杂,静刚度影响因素较多,直接进行刚度测试的试验难度相对大,且需要的试验次数多,消耗物力大。为解决此问题,作者在不同温度下对丁腈橡胶制成的矩形试样进行了静态拉伸试验,对试验得到的应力、应变数据进行拟合得到Mooney-Rivlin超弹性本构模型参数;基于该本构模型对环形丁腈橡胶件的静压缩进行有限元模拟,通过与静态压缩试验结果对比来验证有限元模型的准确性,并利用该有限元模型分析环形丁腈橡胶件的壁厚、外径以及外界环境温度对其静刚度的影响规律。

1 试样制备与试验方法

试验材料为兰州石化生产的N41E丁腈橡胶。采用该材料制备尺寸为43 mm×6 mm×2 mm矩形橡胶件以及如图1所示的环形橡胶件。

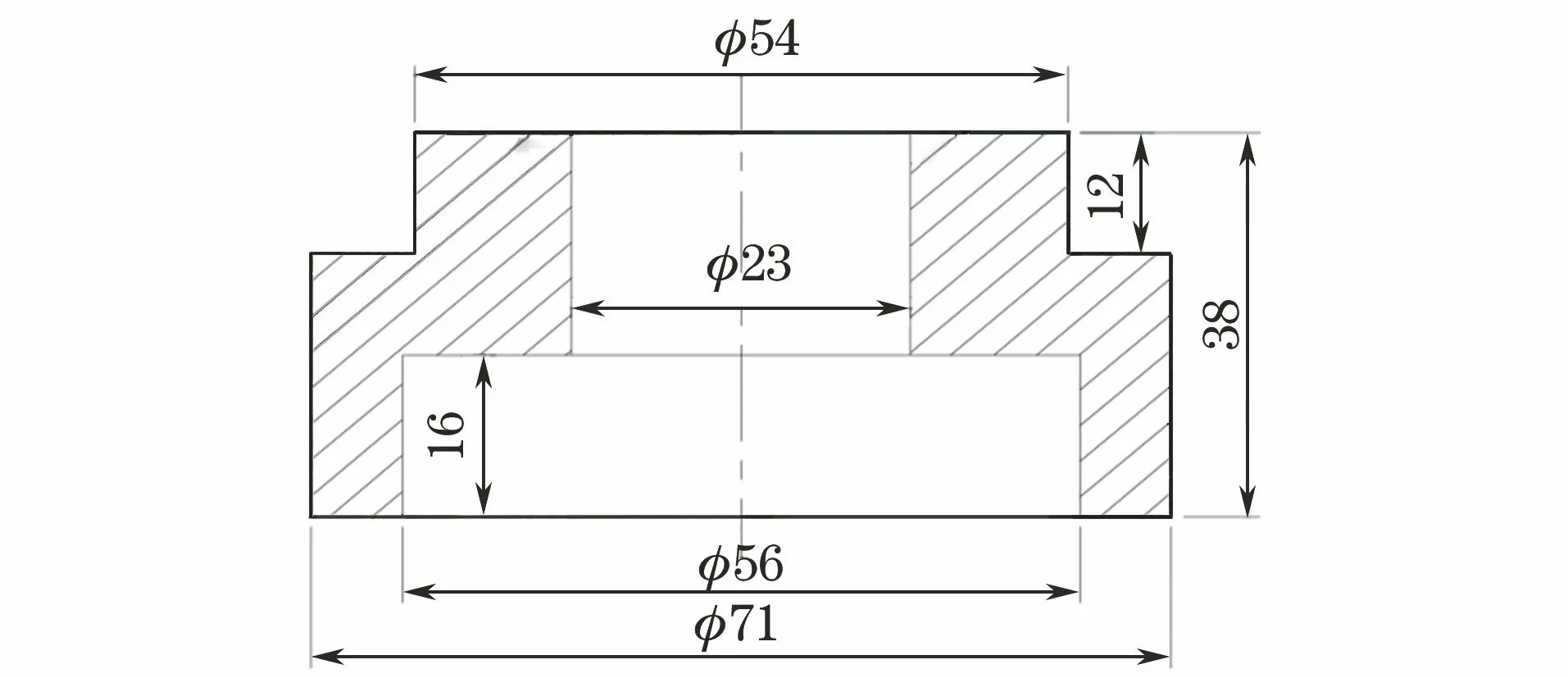
图1 环形丁腈橡胶件的尺寸Fig.1 Dimension of annular nitrile butadiene rubber part

在Eplexor 500N型黏弹谱仪上对矩形丁腈橡胶件进行静态拉伸试验,接触力为1 N,最大拉力为160 N,拉伸应变为150%,试验温度为20～80 ℃。在20 ℃下采用PA20型电液伺服疲劳试验机对环形橡胶件进行静态压缩试验,压缩速度为0.5 mm·min-1,加载位移为3 mm。

2 超弹性本构模型的建立

2.1 理论模型

橡胶是一种各向同性且体积近似不可压缩的材料,具有非线性的超弹性特性。通常用基于应变能密度函数的大弹性变形本构理论来描述拉伸、压缩变形时的超弹性特性,其应变能密度函数[10]模型为

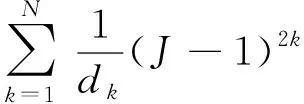
(1)

式中:U为应变能密度;N为项数;Cij为Rivlin系数;i,j,k为整数;dk为与材料的体积压缩性能有关的系数;I1,I2分别为第一、第二应变不变量;J为弹性体积比。

当N=1时,上式可简化[10]为

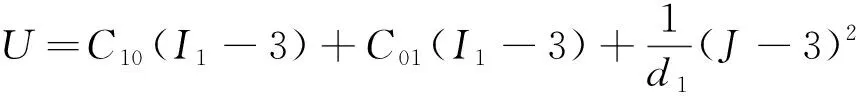
(2)

式中:C10,C01分别为i=1,j=0以及i=0,j=1时的Rivlin系数;d1为k=1时与材料的体积压缩性能有关的系数。

式(2)为橡胶的Mooney-Rivlin超弹性本构模型,确定该模型中材料系数C10,C01,d1的值,即可使用该模型来描述橡胶的超弹性特性。当d1取0时,橡胶为体积完全不可压缩材料。根据超弹性材料所做的功,基于Mooney-Rivlin超弹性模型的应力-应变关系[11]可表示为

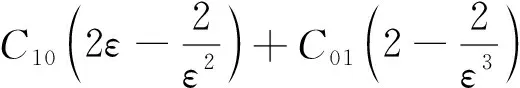
(3)

式中:σ为应力;ε为应变。

2.2 模型参数的确定

将试验获得的矩形丁腈橡胶件在20 ℃静态拉伸时的应力、应变数据输入ABAQUS软件中[10],选择Mooney-Rivlin模型进行数据拟合,结果如图2所示,通过拟合得到的C10,C01,d1分别为0.115 9,0.214 7,0。

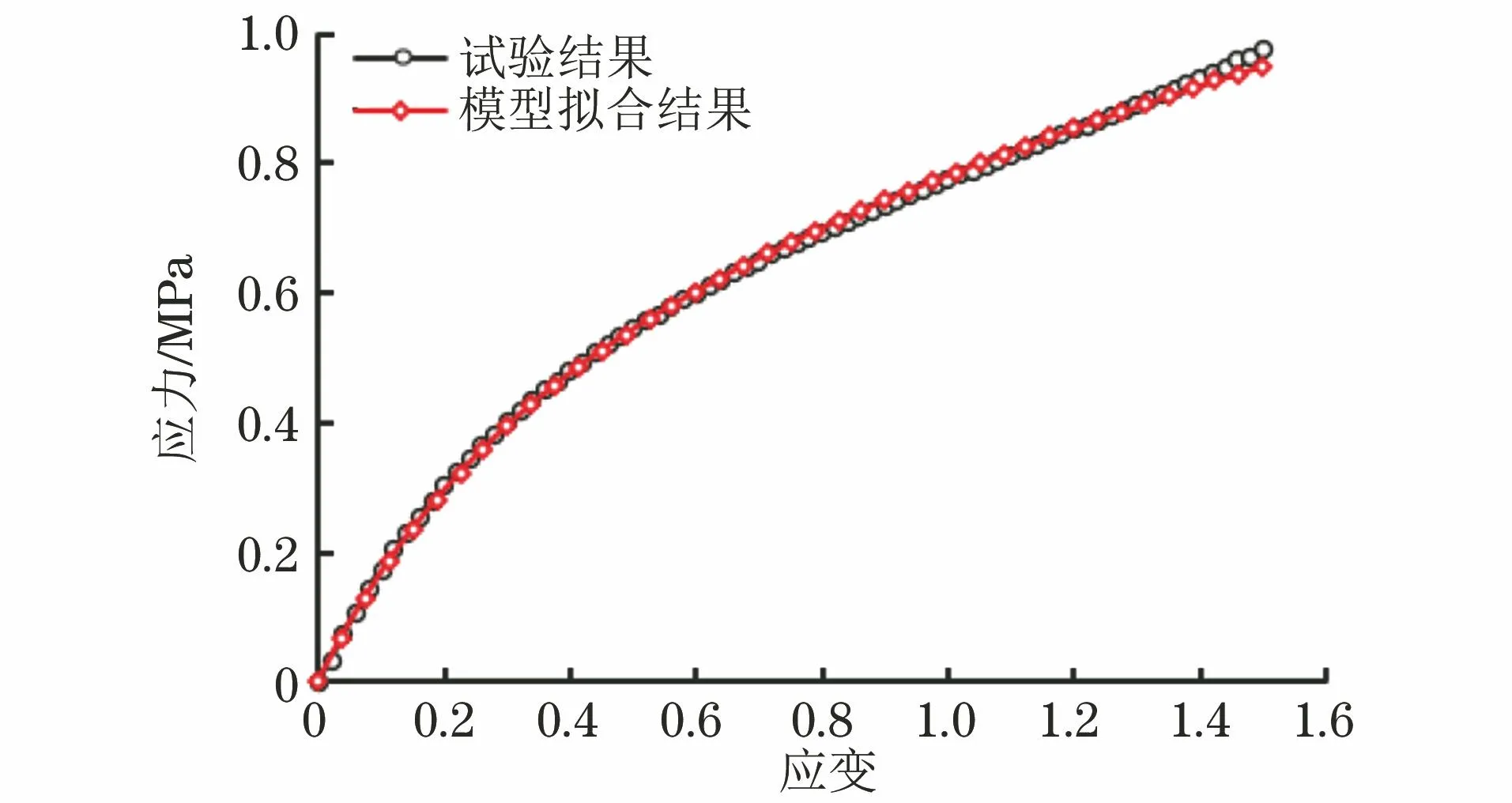
图2 矩形丁腈橡胶件的应力-应变曲线试验结果与模型拟合结果Fig.2 Test and model fitting results of stress-strain curve of rectangular nitrile butadiene rubber part

通过ABAQUS软件建立矩形丁腈橡胶件有限元模型,采用六面体减缩积分杂交单元C3D8H划分网格,如图3所示。材料密度设为1.26×10-9t·mm-3,将拟合得到的20 ℃下的模型参数输入到模型中,设定静态分析步1 s,对丁腈橡胶件上端面施加位移载荷约束,下端面施加固定约束,采用所建立的有限元模型进行静态拉伸仿真分析。

图3 矩形丁腈橡胶件的有限元模型Fig.3 Finite element model of rectangular nitrile butadiene rubber part

由图4可以看出,静态拉伸仿真得到的力-位移曲线与试验得到的曲线重合性很好。当位移小于1 mm时,仿真与试验结果间的相对误差最大达到20%;当位移大于1 mm时,相对误差小于5%。由于一般对橡胶材料进行大变形处理,小变形阶段的误差对仿真结果影响不大,因此Mooney-Rivlin超弹性本构模型可以准确描述丁腈橡胶件的超弹性特性。按照同样的方法可以获得丁腈橡胶在不同温度下的Mooney-Rivlin模型参数,结果如表1所示。

表1 不同温度下丁腈橡胶的Mooney-Rivlin模型参数Table 1 Mooney-Rivlin model parameters of nitrile butadiene rubber at different temperatures

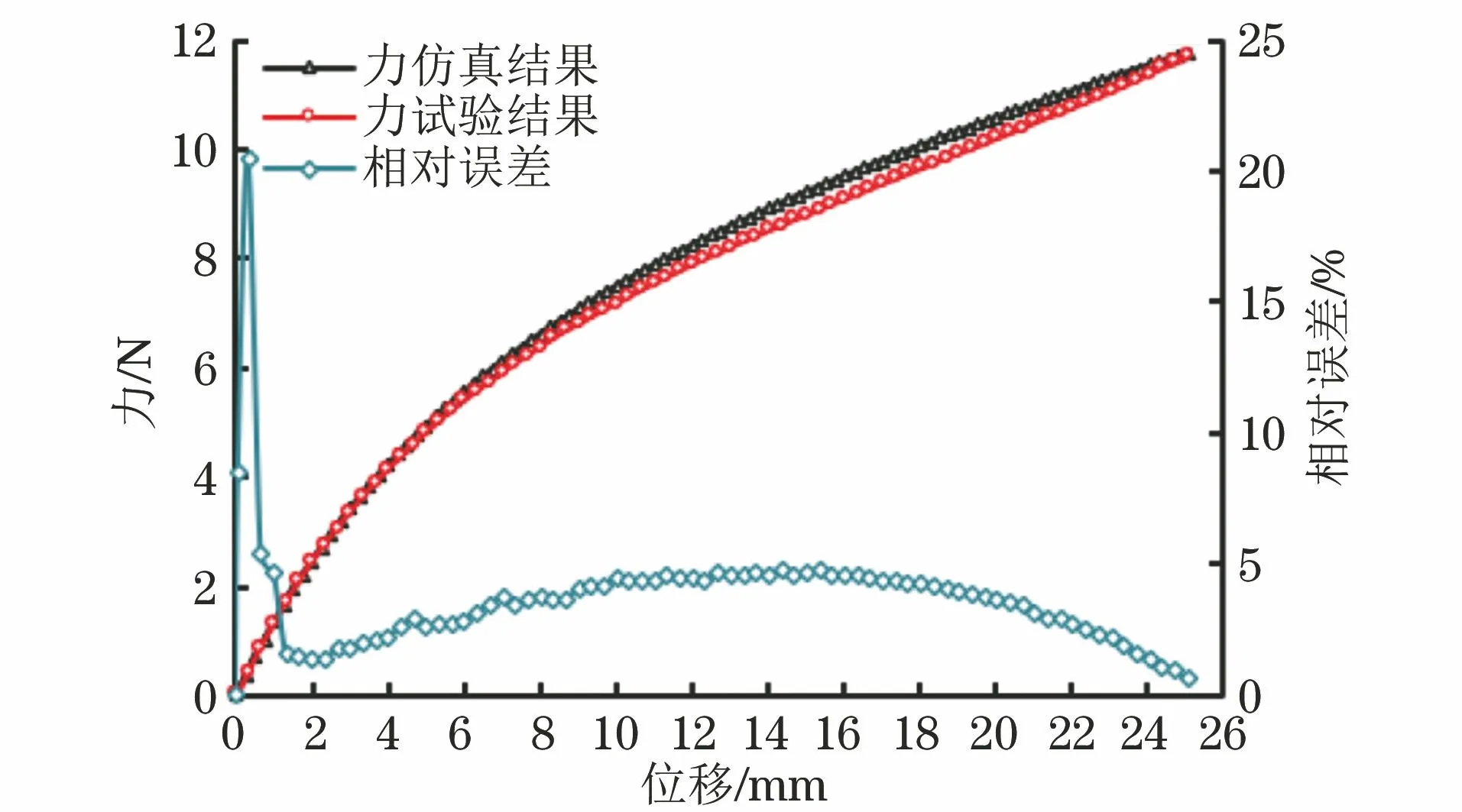
图4 矩形丁腈橡胶件的力-位移曲线试验结果与仿真结果以及相对误差Fig.4 Test results and simulation of force-displacement curves of rectangular nitrile butadiene rubber part and relative errors

3 环形丁腈橡胶件静刚度的有限元模拟

3.1 有限元模型的建立

按照静态压缩试验所用环形件的结构和尺寸,采用ABAQUS软件建立环形丁腈橡胶件的几何模型,如图5所示,支撑螺杆为橡胶件提供轴向支撑并限制轴向位移,橡胶件安装在支撑螺杆上,工作时螺杆下端固定,橡胶件轴向受力。螺杆材料为40CrMo钢,在ABAQUS软件中赋予其密度为7.9×10-9t·mm-3,弹性模量为206 000 MPa,泊松比为0.3[12]。超弹性材料在拉伸和压缩时可使用同一本构模型[13],将丁腈橡胶的超弹性本构模型参数输入到模型中。支撑螺杆采用C3D10单元划分网格,环形丁腈橡胶件使用C3D8H六面体单元划分网格。设定Static General分析步,将大变形开关打开;环形丁腈橡胶件与中心支撑螺杆接触的水平表面和垂直表面设定法向硬接触和切向无摩擦接触,在支撑螺杆下表面施加全方向的固定约束,设定参考点,与环形丁腈橡胶件受载面建立耦合关系,耦合点记为RP。

3.2 试验验证

采用所建立的有限元模型在相同的试验参数下对环形丁腈橡胶件进行20 ℃静态压缩模拟,并将模拟得到的力-位移曲线与试验结果进行对比。由图6可以看出,在小位移阶段,模拟得到的力-位移曲线与试验结果吻合较好,随着位移的增大,模拟结果和试验结果的误差增大,但相对误差仍小于15%。环形丁腈橡胶件静刚度Ks的计算公式[14]为

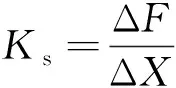
(4)

式中:ΔF,ΔX分别为静态加载结束时的加载力与变形量。

由模拟结果计算得到的静刚度为268 N·mm-1,试验静刚度为237 N·mm-1,相对误差为13.1%,验证了该有限元模型的可靠性。因此,可以采用该有限元模型对环形丁腈橡胶件的静态压缩行为进行模拟。

3.3 壁厚对环形丁腈橡胶件静刚度的影响

保持环形丁腈橡胶外径(54 mm)不变,建立壁厚分别为26,31,36 mm的环形丁腈橡胶件三维模型,导入ABAQUS软件中进行静态压缩模拟,材料本构模型及边界条件保持不变,对RP点施加3 mm位移约束载荷,模拟得到的力-位移曲线如图7所示。计算得到,壁厚为26,31,36 mm的环形丁腈橡胶件的静刚度分别为362.72,271.75,242.13 N·mm-1,可见随着壁厚的增加,环形丁腈橡胶件的静刚度减小。这是因为壁厚越大,相同载荷下环形丁腈橡胶件的压缩变形量越大,导致其静刚度越小。

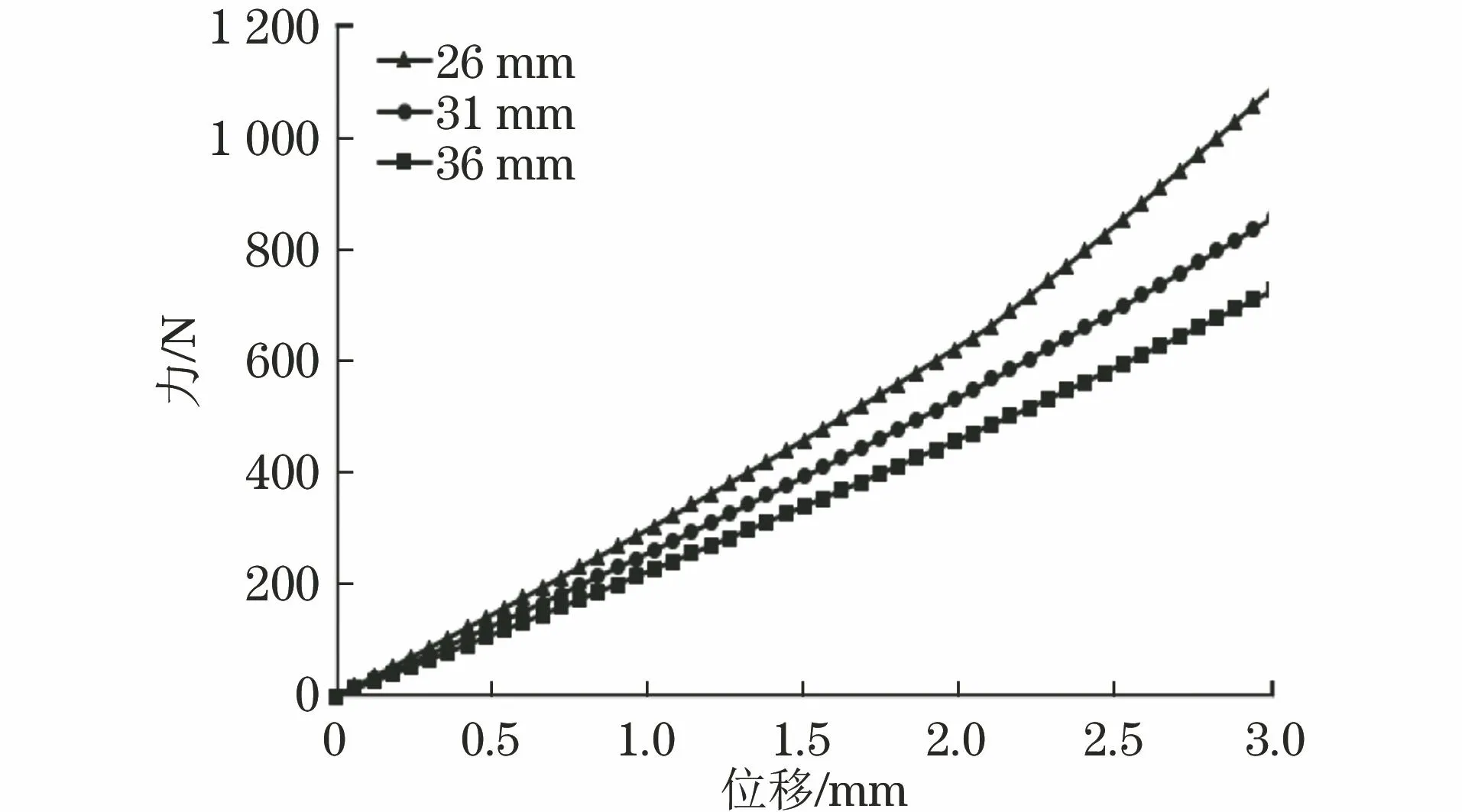
图7 不同壁厚环形丁腈橡胶件的力-位移曲线(外径54 mm,温度20 ℃)Fig.7 Force-displacement curves of annular nitrile butadiene rubber part with different wall thicknesses (outer diameter of 54 mm and temperature of 20 ℃)

3.4 外径对环形丁腈橡胶件静刚度的影响

保持环形丁腈橡胶件的壁厚(26 mm)不变,建立外径分别为54,60,66 mm的环形丁腈橡胶件三维模型,导入ABAQUS中进行静态压缩模拟,材料本构模型及边界条件保持不变,分别对RP点施加3 mm位移约束载荷,模拟得到的力-位移曲线如图8所示。计算得到,外径为54,60,66 mm的环形丁腈橡胶件的静刚度分别为362.72,206.5,149.2 N·mm-1,可见随着外径的增加,环形丁腈橡胶件的静刚度减小。这是因为外径越大,相同载荷下环形丁腈橡胶件的压缩量越大,导致静刚度越小。

图8 不同外径环形丁腈橡胶件的力-位移曲线(壁厚26 mm,温度20 ℃)Fig.8 Force-displacement curves of annular nitrile butadiene rubber part with different outer diameters (wall thickness of 26 mm andtemperature of 20 ℃)

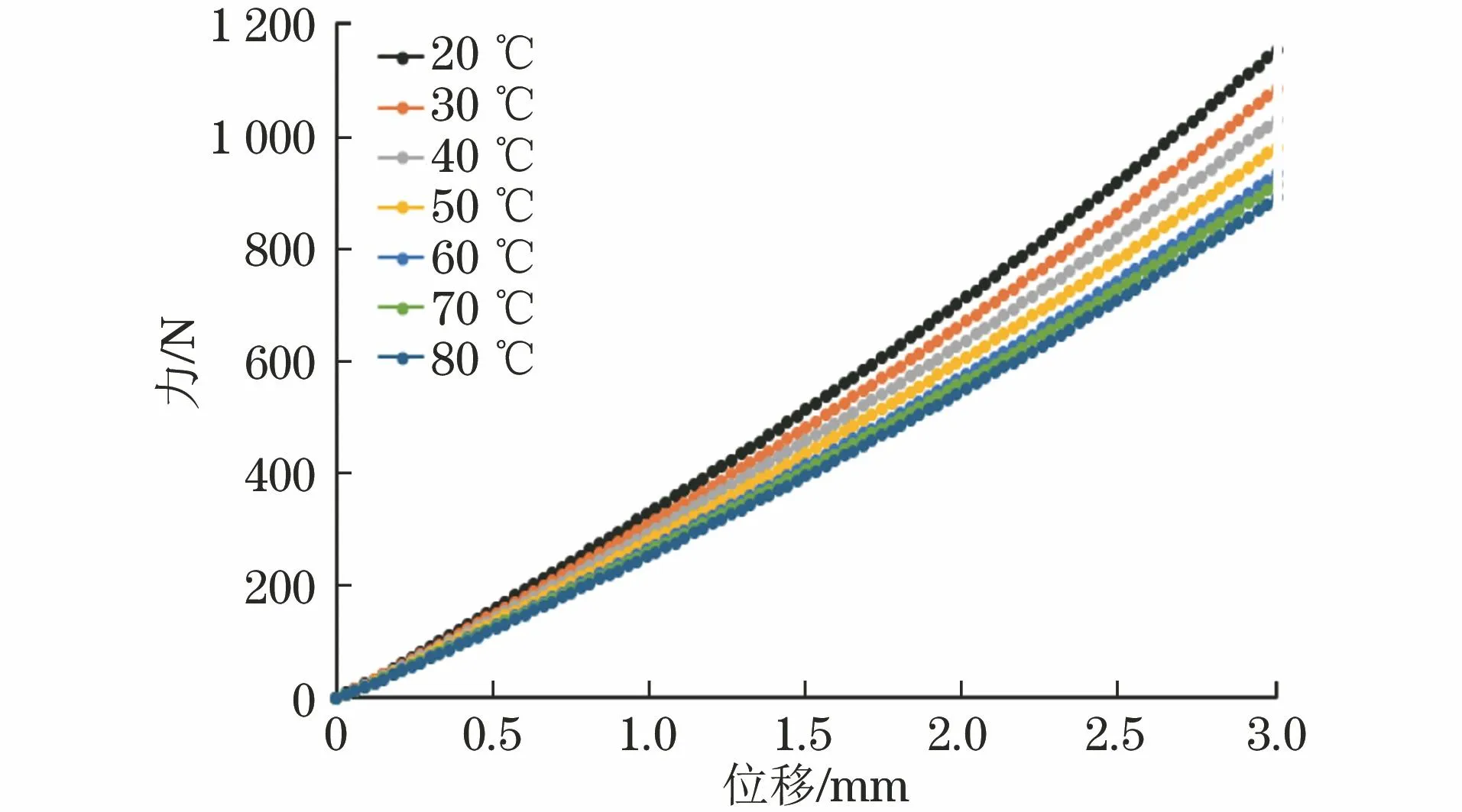
图9 不同温度下环形丁腈橡胶件的力-位移曲线(壁厚26 mm,外径54 mm)Fig.9 Force-displacement curves of annular nitrile butadiene rubber part at different temperatures (wall thickness of 26 mm and outer diameter of 54 mm)

3.5 温度对环形丁腈橡胶件静刚度的影响

保持环形丁腈橡胶件的壁厚(26 mm)和外径(54 mm)不变,建立环形丁腈橡胶件三维模型,导入ABAQUS软件中进行不同温度(20,30,40,50,60,70,80 ℃)的静态压缩模拟,根据表1中的模型参数定义不同温度下的材料属性,边界条件保持不变,对RP点施加3 mm位移约束载荷,模拟得到的力-位移曲线如图8所示。计算得到,20,30,40,50,60,70,80 ℃下,环形丁腈橡胶件的静刚度分别为362.72,343.81,327.56,315.75,306.68,300.25,296.49 N·mm-1,可见随着温度的升高,环形丁腈橡胶件的静刚度减小,且减小速率逐渐减慢。这是因为随着温度的升高,橡胶分子间相互作用减弱[15]。

4 结 论

(1) 基于Mooney-Rivlin超弹性本构模型,通过有限元方法模拟得到矩形丁腈橡胶件静态拉伸大变形阶段的力-位移曲线与试验结果相吻合,相对误差小于5%,表明Mooney-Rivlin超弹性本构模型可准确描述丁腈橡胶的超弹性特性。

(2) 基于矩形丁腈橡胶件静态拉伸模拟得到的模型参数,通过有限元方法模拟得到环形丁腈橡胶件在20 ℃静态压缩力-位移曲线与试验结果吻合较好,相对误差小于15%,计算得到的静刚度相对误差为13.1%,验证了该有限元方法的准确性。

(3) 采用上述模拟方法研究发现:随着壁厚或外径增加,环形丁腈橡胶件的静刚度减小;随着温度的升高,静刚度减小,但减小速率逐渐降低。