云爆超压对火箭车内有生力量毁伤评估研究

周炜智, 李 强, 李 波, 杜 烨

(中北大学 机电工程学院, 太原 030051)

0 引言

随着科学技术的不断进步,武器系统迅速发展。为适应远程化、精确化的作战需求,大量高新科技投入到了现代火箭炮武器系统的研发改进中,增强了该武器系统的作战能力。现代火箭炮武器系统在射程、覆盖范围及单位火力密度方面拥有较大的优势[1],是火力输出的主要力量之一。因此,在作战中火箭炮武器系统也必将成为我军打击的重点目标。但随着火箭炮武器系统轻型化的改革,火箭炮在具备一定防护能力的基础上,拥有着强大的机动性,能极大程度规避点杀伤形式的打击,大大增加了我军打击行动的难度。

在现有的武器系统中,云爆弹是一种特殊的面杀伤武器。在作用时,首先抛洒云爆剂散布至空气中,形成气溶胶云团,随后将其引爆,形成冲击波效应、热效应、窒息效应等[2-3]。其中,爆炸冲击波是云爆弹主要的毁伤源[4-6],加以出色的杀伤范围,可对有生力量、软目标造成很大的毁伤威力,可有效针对火箭发射车机动性强、反应快的特点,威胁火箭发射车内有生力量的生命安全,进而达到有效打击火箭炮武器系统的目的。

为掌握云爆弹毁伤效能,准确把握云爆弹在特定作战情形下的毁伤效果,许多学者进行了研究。许化珍等[7]提出了云爆弹效能评估数学模型,可估算云爆弹的杀伤范围,并指出散布均方差对云爆弹杀伤效能的影响。刘想炎等[8]基于云爆弹超压和热辐射效应,建立了云爆弹对地面人员的综合毁伤评估模型。叶军等[9]提出了云爆弹冲击波效应对单个地堡内有生力量的封锁评估模型。刘、叶二人分别对相应作战条件下,云爆弹的打击效果进行了评估。但如今作战形式多元,远程作战趋势明显。火箭炮武器系统作为远程化作战的代表,为进行有效打击,如何评估云爆弹对目标的毁伤效果成为亟待解决的问题。

本研究中为解决云爆弹冲击波超压效应对火箭发射车内有生力量的杀伤评估问题,从云爆弹在地面超压分布的实验数据出发,采用AUTODYN软件数值模拟计算,获得火箭发射车内超压分布场,并结合超压杀伤判据,提出一种基于蒙特卡洛方法的针对火箭发射车内人员的毁伤评估模型。研究结果可用于云爆弹毁伤效能的评估,为云爆弹设计提供参考。

1 车内超压的数值计算方法及等效性验证

为探究云爆弹面杀伤特性对火箭发射车目标的打击效果,以160 kg装药的ZBD-2型云爆弹[10]为例,研究分析云爆弹在火箭发射车前方不同弹目相对距离下起爆的毁伤效果。

1.1 超压数值计算模型

本研究中以俄制BM-30型“龙卷风”式火箭炮系统为研究对象,火箭发射车由供2人呈纵列乘坐的驾驶/指挥室和供2人并列操作的火力控制室[11]组成。模型采用拉格朗日网格建立,为保证计算效率,对模型简化。其中,驾驶/指挥室前端车窗以及火力控制室两侧车窗不设置车窗玻璃,简化冲击波传播过程。相关参数如表1所示。

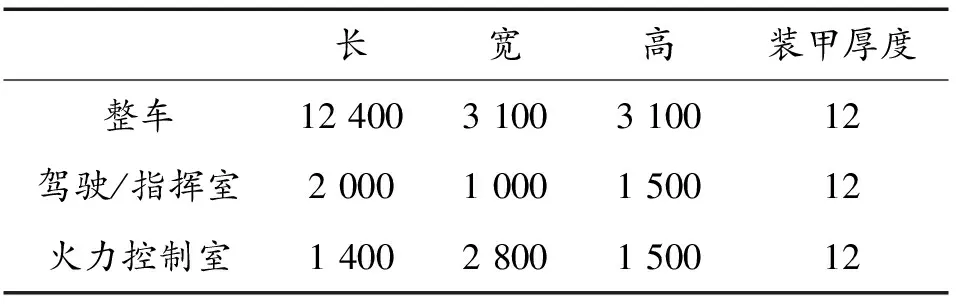
表1 火箭发射车模型尺寸

云爆弹采用圆柱体结构。考虑到实际情形中弹目相对距离远、冲击波传播距离长,为加快求解的速度,将模型进行缩减。对于各个弹目相对距离工况,将云爆弹与火箭发射车的相对位置固定、装药等效处理,并保证等效计算所得车内超压与实验结果一致。

空气域采用欧拉网格建模,模型尺寸为17 000 mm×4 500 mm×8 000 mm,网格尺寸25 mm。边界条件除底面设置为刚性反射,其余边界采用FLOW_OUT流出边界。数值计算模型如图1所示。

图1 车内超压数值计算模型

1.2 材料参数

结合文献[12-13]的经验,本研究中采用TNT等效模拟云爆弹爆炸所产生的超压效果。爆源状态方程采用JWL方程描述。火箭发射车材料选用装甲钢[14],采用Linear状态方程以及Johnson-Cook强度模型描述。空气视为理想气体状态,气体密度为1.225×10-3g/cm3,比内能取2.068×105μJ/mg。具体的材料模型及参数[15]如表2—表4所示。

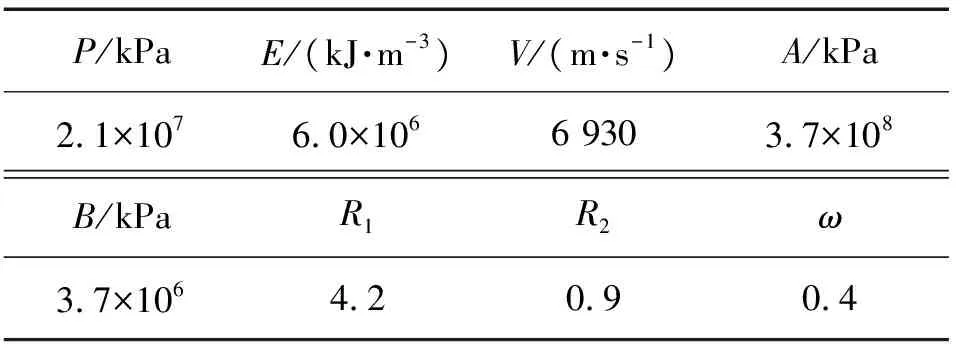
表2 JWL状态方程参数

表2中,P为爆轰压力;E为初始内能;V为比容;A、B、R1、R2、ω为材料的特征参数。

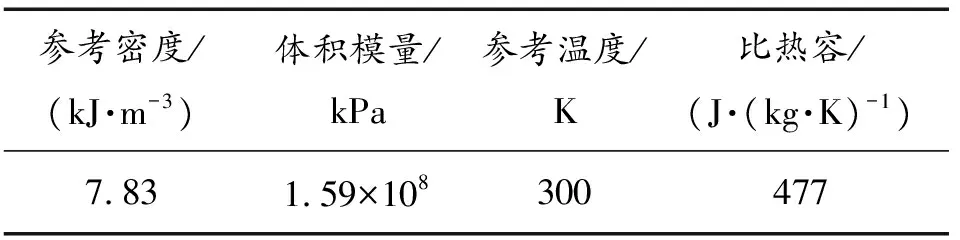
表3 Linear状态方程参数

表4 Johnson-Cook强度模型参数

表4中,G为剪切模量;σy为屈服应力;CH为硬化常数;n为硬化指数;Cs为应变力常数;m为热软化指数;T为参考温度。

1.3 计算条件设置

为方便分析,对车内坐标系进行定义。坐标系原点O的位置如图2、图3所示。OX轴沿车体纵向,指向驾驶/指挥室。OY轴垂直于OX轴,沿横向指向车尾。OZ轴垂直于OXY平面,以沿竖直方向指向车顶为正,且符合右手螺旋定则。因此,X、Y、Z轴坐标可分别代表火箭发射车内各点在纵、横、竖向的位置。

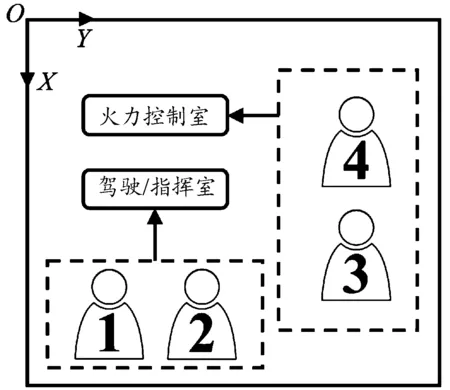
图2 人员分布示意图 Fig.2 Diagram of personnel distribution

结合火箭发射车结构功能,可知火箭发射车内人员的主要位置分布,如图2所示。其中,1为主驾驶区、2为副驾驶区,负责火箭发射车的驾驶和指挥;3、4为火力控制一、二区,负责弹道校准以及操纵发射。车内人员姿态可分为坐姿和跪姿2种,分别模拟车内人员正常驾驶以及应急躲避状态。观测点设置位置如图3所示,其中,#1、#2、#5、#6为主驾驶区,#3、#4、#7、#8为副驾驶区,#9、#12为火力控制一区,#11、#14为火力控制二区,#10、#13为火力控制室中央。此外,#1～#4、#9～#11观测点位于坐姿平面,用于测量人员坐姿所受的超压峰值;#5～#8、#12～#14观测点位于跪姿平面,用于测量人员跪姿所受的超压峰值。

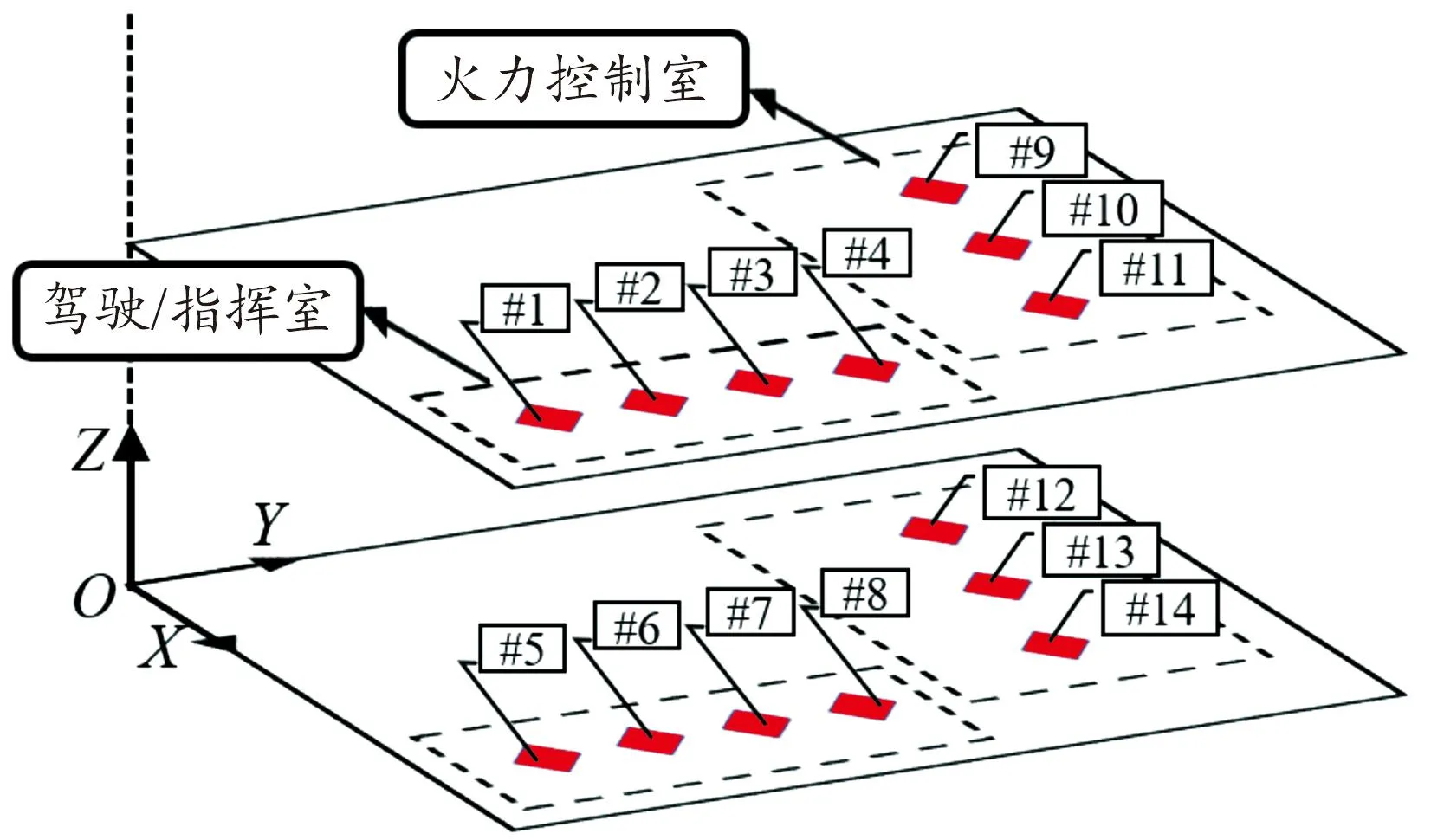
图3 观测点布置示意图

1.4 数值计算方法等效性验证

由于本文中仅探究云爆弹冲击波超压效应的杀伤效果,暂不考虑热效应的影响。当弹目相对距离大于18 m时,超压效应为主导杀伤因素。因此,基于实验数据,选取云爆弹与火箭发射车弹目相对距离为18、25、30、35、40、45、48 m的7种工况模拟计算,获得各工况下云爆弹在火箭发射车内形成的超压分布场。

起爆如图1所示位置处的TNT,将计算所得TNT在车头前端产生的超压与云爆弹在18～48 m处的实验数值对比,使两者相差小于1%。从而确定各个相对弹目距离工况下云爆弹超压效果所对应的等效TNT当量,结果如表5所示。

表5 实验数据与等效结果对比

考虑到火箭发射车横向长度不超过3.4 m,且随距离的增加,TNT产生的冲击波超压衰减效果相较于云爆弹愈加明显。为验证利用TNT等效模拟云爆弹爆炸冲击波超压分布的合理性,以弹目相对距离后3.4 m处的超压值为依据,对比分析此处等效当量TNT与云爆弹在空气中产生的冲击波超压值,结果汇总于表5。

表5中,计算结果与实验所测超压峰值误差均小于10%。因此,基于本节所述数值计算方法,起爆表5中各等效当量的TNT,可分别模拟云爆弹在相应弹目相对距离工况下对火箭发射车内产生的超压效应。

2 车内超压计算结果分析

采用第1节所述超压数值计算方法,分别起爆表5所示等效当量的TNT,获得弹目相对距离为18、25、30、35、40、45、48 m时云爆弹在火箭发射车内形成的超压。将计算结果对比分析,探究弹目相对距离、乘员姿态以及车内位置3因素对火箭车内的超压分布场的影响。

2.1 冲击波在火箭发射车内的传播规律

由爆炸相似率可知,云爆弹在不同弹目相对距离下起爆,产生的冲击波在火箭发射车内的传播过程均一致。因此,以弹目相对距离为25 m的工况为例,对冲击波传播过程进行分析,如图4所示。冲击波首先以图4(b)中箭头所指方向,由火箭发射车前端车窗进入驾驶/指挥室,并向室内传播,如图4(c)所示。在驾驶/指挥室中,由于受到车体壁面的约束作用,冲击波经壁面反射产生反射波。反射波和入射波的相互作用,使得图4(d)中所示驾驶/指挥室内的高压区Ⅰ的范围大于室外的高压区Ⅱ的范围。随后,冲击波依次沿图4(e)、图4(f)中箭头所指方向,由火箭发射车通风系统以及火力控制室车窗进入火力控制室内,并向室内传播。

2.2 乘员姿态对超压分布的影响

冲击波在传播至车内底面时形成反射,继而向反方向传播。跪姿平面与室内底面的距离较近,反射波作用效应更加明显,使得当其余条件均一致时,乘员跪姿所受的超压始终高于坐姿,如图5所示。

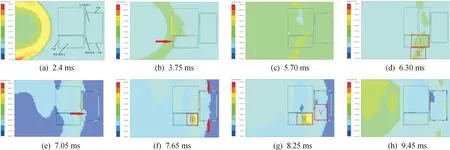
图4 弹目相对距离为25 m时压力云图随时间的变化

图5 弹目相对距离为25 m时车内区域的压力云图

图6展示了不同弹目相对距离下车内同一位置坐、跪姿平面超压峰值的差异。对比分析各位置处坐、跪姿平面的超压峰值可知,火箭发射车内主、副驾驶区处乘员跪姿所受超压高于坐姿乘员的18%～27%;火力控制一、二区处乘员跪姿所受超压高于坐姿乘员的3%～8%。

2.3 火箭发射车内位置对超压分布的影响

图7为不同弹目相对距离下驾驶/指挥室内坐、跪姿平面的超压分布场。考虑到驾驶/指挥室内乘员呈横向分布,故对驾驶/指挥室内超压随横向距离(Y轴)的变化进行分析。图7中表明,驾驶/指挥室内坐、跪姿平面的超压分布的规律均为:随着横向距离的增加,超压峰值先衰减后增加。在坐姿或跪姿平面内,副驾驶区域的超压将高于主驾驶区域超压的4%～12%。

为探究图7趋势变化的机理,以弹目相对距离为25 m工况为例,对驾驶/指挥室坐姿平面内各处超压随时间的变化进行分析。图8展示了该工况下对应观测点#1～#4的超压-时间曲线。

图6 超压峰值和弹目相对距离关系曲线

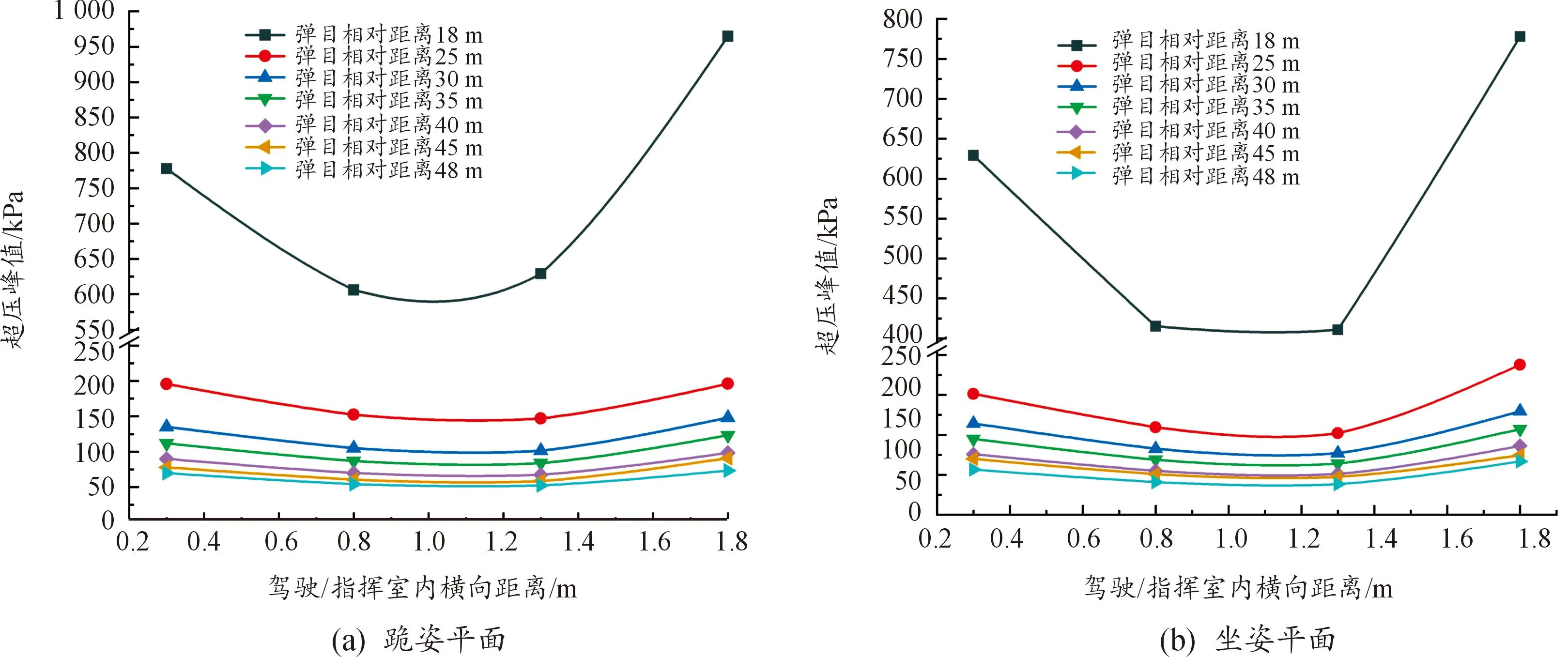
图7 驾驶/指挥室内超压随横向距离变化关系图

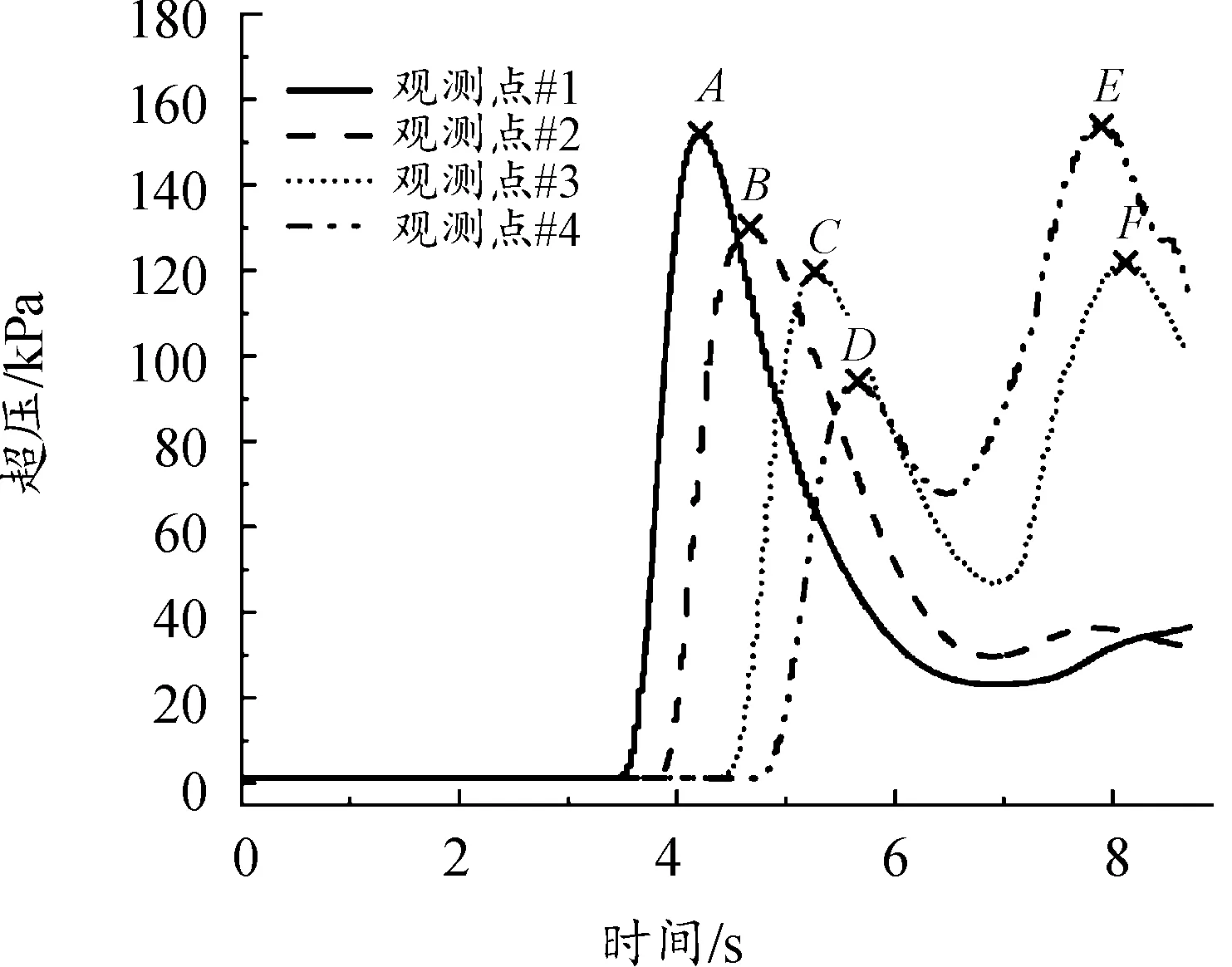
图8 弹目相对距离为25 m时各观测点的超压-时间曲线

图8中,随着时间的推移,观测点#1～4依次出现超压峰值点A、B、C、D,且超压峰值递减,符合冲击波传播过程中超压衰减规律。但观测点#3、#4的超压-时间曲线均出现2个峰值,且超压峰值ΔPE>ΔPA>ΔPB>ΔPF。结合冲击波传播理论[16-17],A、B、C、D为入射波超压峰值点,E、F为反射波超压峰值点。通过冲击波传播过程可知,在驾驶/指挥室横向末端产生高压区域,如图4 (f)、图4(g)中Ⅲ、Ⅳ区域所示。证明冲击波在驾驶/指挥室横向末端反射,使得驾驶/指挥室内副驾驶区的超压高于主驾驶。

对于火力控制室内的超压分布场,由于火力控制室内乘员呈纵向分布,对火力控制室内超压分布沿纵向(X轴)进行分析,如图9所示。

图9中,在同一姿态平面内,随着纵向距离的增加,火力控制室内超压峰值先减小后增大。结合2.1节中冲击波在火力控制室内的传播过程可知,冲击波由两侧同时进入室内,传播至中间位置处发生叠加,如图4(f)、图4(h)所示,使得室内同一姿态平面内超压的最小值与最大值之比大于97%。此外,由于火箭发射车通风系统的存在,驾驶/指挥室内的冲击波将穿透通风系统并传播至火力控制室内,与空气中传播至室内的冲击波叠加,如图4(g)中Ⅴ区域所示,导致火力控制一区的超压峰值略高于火力控制二区0.5%～2.5%,故忽略冲击波穿透通风系统所引起的超压。因此,结合以上2点可认为火力控制一、二区同一姿态平面内的超压一致。

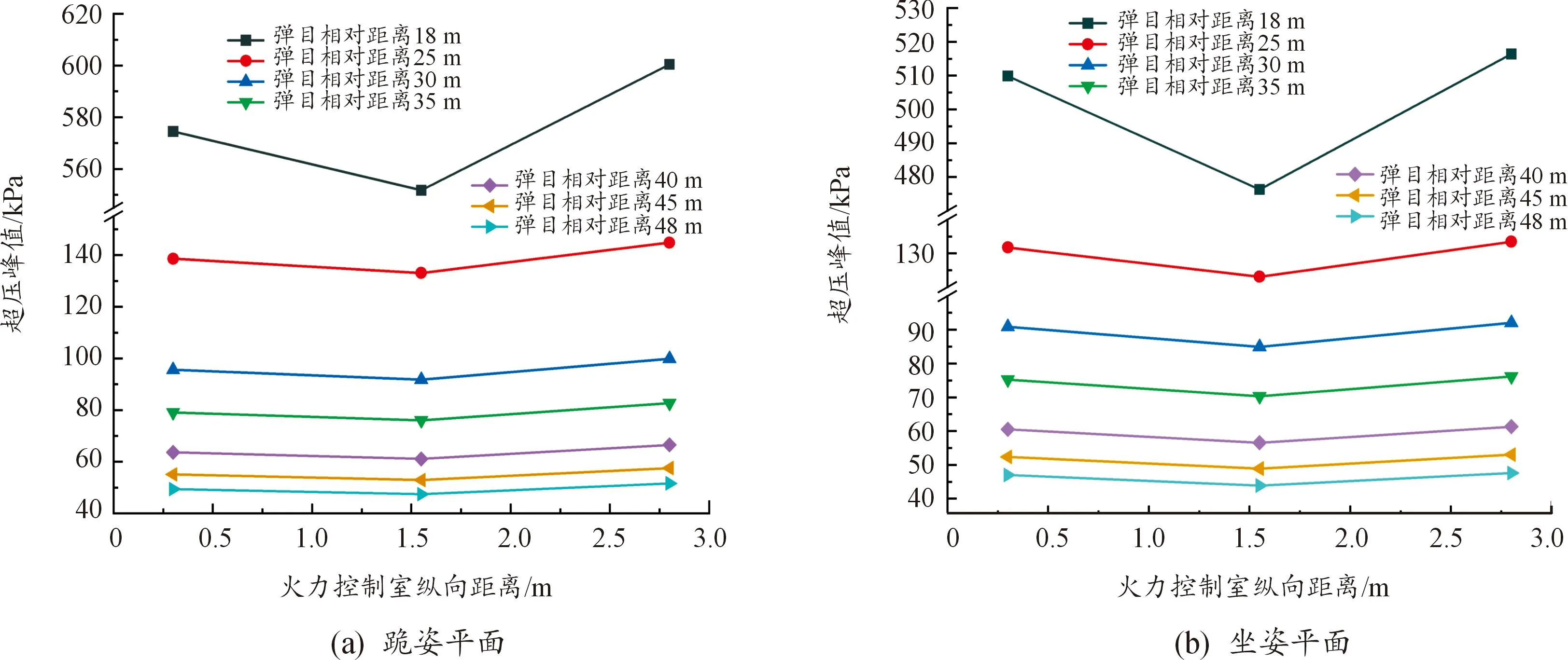
图9 火力控制室内超压随纵向距离变化关系

3 毁伤评估模型的建立及验证

为研究云爆弹超压对火箭发射车内人员的毁伤效应,本文中采用蒙特卡洛方法[9]建立毁伤评估模型。首先,明确冲击波超压对有生力量的杀伤判据、构造火箭发射车内人员状态的随机问题。其次,根据已知概率分布随机抽样,并结合第2节所得车内超压分布,确定车内人员状态以及受伤等级。通过不断重复试验,以频率表示概率,获得云爆弹对火箭发射车内人员的封锁率,构建毁伤评估模型并验证。

3.1 超压对有生力量的杀伤判据

云爆弹对有生力量的易损性主要取决于爆炸时伴生的超压峰值和瞬时风动压的幅度与持续时间[7]。文献[16]给出了人员不同伤亡程度时的毁伤超压阈值,见表6所示。

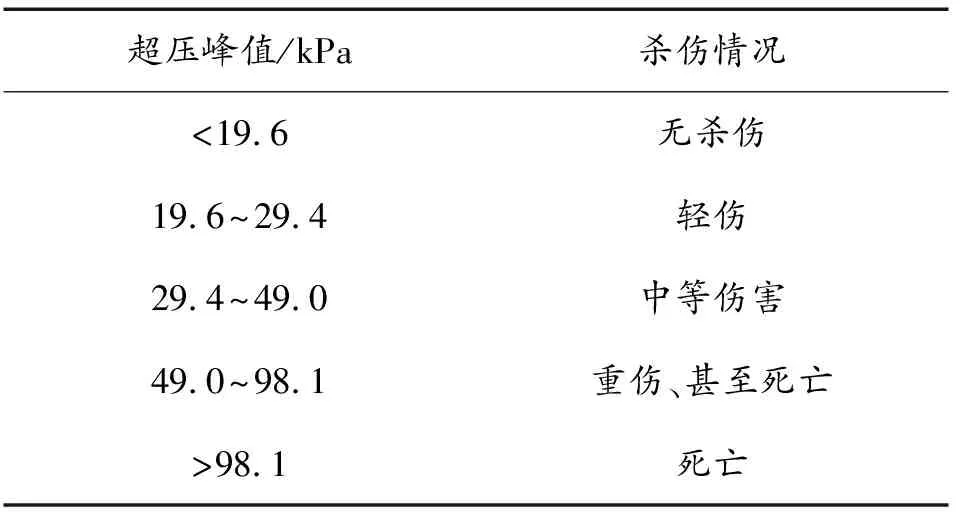
表6 冲击波超压对人的杀伤判据

3.2 车内有生力量状态分析

火箭发射车主要有发射以及行驶2种状态,设2种状态发生的概率均为50%。在分析火箭发射车行驶状态时,考虑到火箭发射车行驶速度相较于冲击波传播速度可忽略不计[16],将行驶状态的火箭发射车同发射状态视为静止。因此,在本研究中火箭发射车的状态仅影响着人员的分布。

火箭发射车在执行作战任务时,需有4名炮班成员。其中,2人呈纵列坐在前部的驾驶/指挥室中,另外2人并排坐在底盘前部的火力控制室中。但当火箭发射车进入战斗状态时,车内炮班成员可能由于支援、伤亡等因素而导致人手不足。当车内不满员时,行驶状态的火箭发射车,人员将集中分布于驾驶/指挥室,且优先处于主驾驶位置;发射状态的火箭发射车,人员将集中分布于火力控制室中。因此,可对火箭发射车内人员分布情况做出假设,结果如表7、表8所示。

表7 火箭发射车行驶状态车内人员分布统计

表8 火箭发射车发射状态车内人员分布统计

对于各个位置处的车内人员,均有坐姿和跪姿2种姿态,且设2种姿态发生的概率均为50%。

3.3 封锁结果计算

图10为云爆弹对火箭发射车内有生力量的毁伤评估流程。基于3.2节内容,对车内人员的数量、位置以及姿态随机抽样。结合第2节车内超压分布的仿真计算结果以及表6所示的判定依据,确定云爆弹对车内人员的杀伤等级。将杀伤结果与封锁条件进行比对,判断是否成功封锁火箭发射车内有生力量。重复以上过程N次,获得不同弹目相对距离条件下云爆弹对火箭发射车内有生力量的封锁率。

以火箭发射车内有生力量全部死亡为成功封锁火箭发射车的判定标准,基于图10所示流程对不同弹目相对距离的情况分别模拟计算 100 000 次,所得结果表9所示。

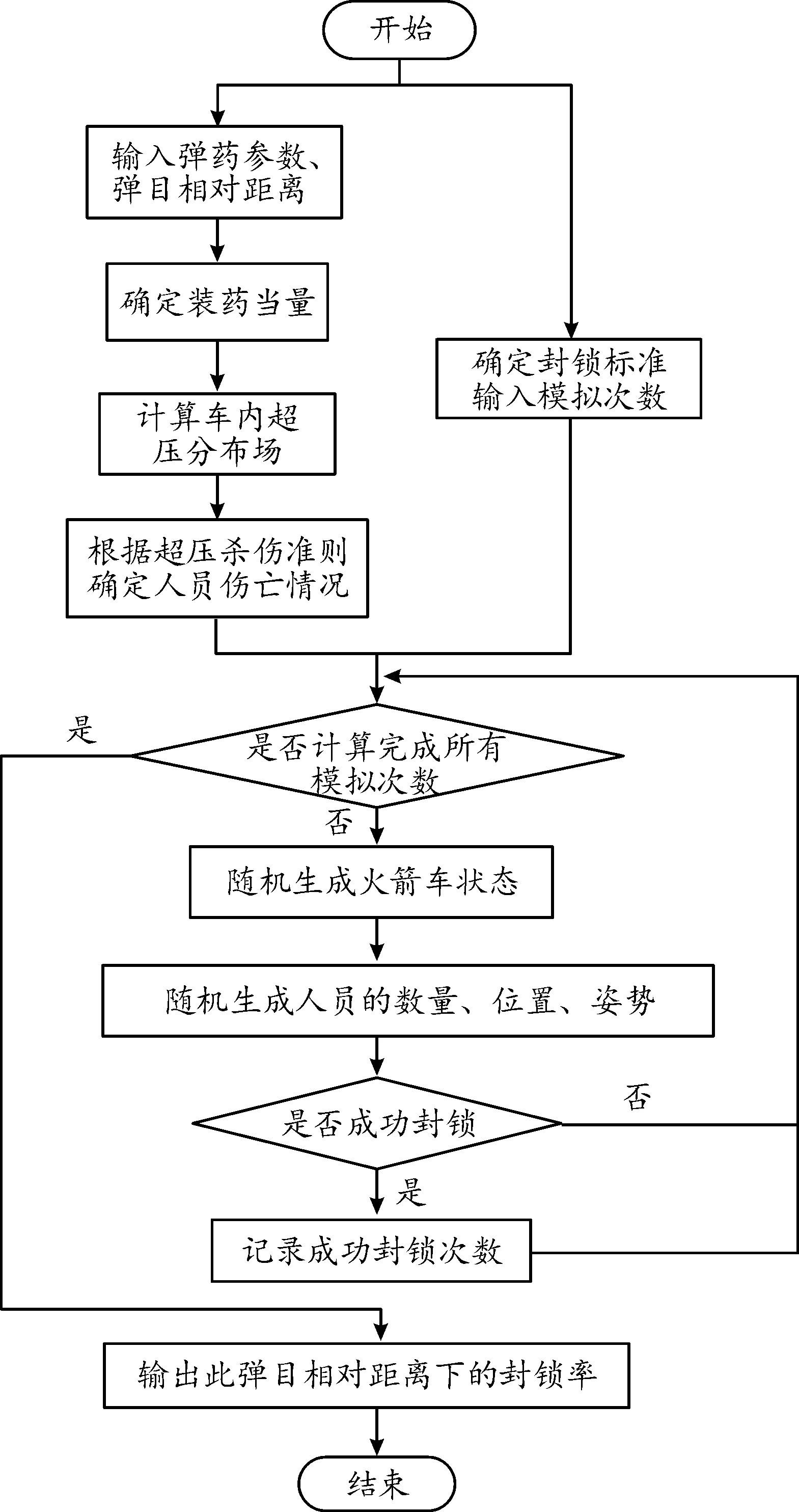
图10 毁伤评估流程框图

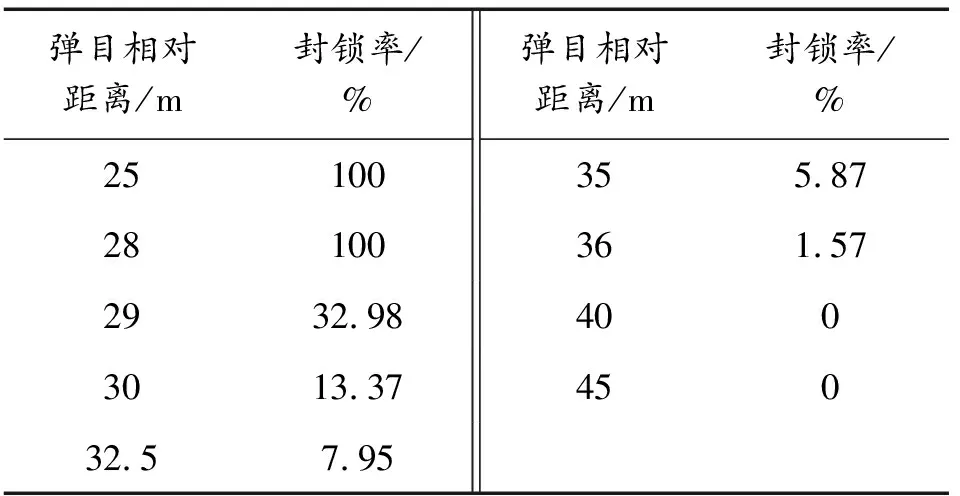
表9 160 kg装药云爆弹对各弹目相对距离 车内人员封锁率

由表9中数据可知,云爆弹对火箭发射车内有生力量的封锁率随弹目相对距离的增加而递减。对于160 kg装药的云爆弹,在弹目相对距离小于28 m时,火箭发射车内有生力量全部死亡,云爆弹可对火箭发射车成功封锁。在弹目相对距离大于36.35 m时,车内有生力量均存活,将丧失对火箭发射车的封锁能力。当弹目相对距离为在弹目相对距离为28～36.35 m,结合第2节中车内超压的分布规律可知,随着弹目相对距离的增加,云爆弹将依次丧失对火力控制二区、一区、主驾驶区以及副驾驶区内坐、跪姿人员封锁能力,从而导致对火箭发射车内有生力量的封锁率下降。

3.4 毁伤评估模型的建立

由爆炸相似率可知,相似的爆炸现象之间在几何和力学上具有相同的规律性[16]。因此,可通过表9中封锁率随弹目相对距离的变化趋势,得出几何相似云爆弹的毁伤评估模型。并结合云爆超压的衰减规律,对模型修正完善,建立适用性强的云爆超压对火箭发射车内有生力量的毁伤评估模型。

由表9中数据可得,云爆超压对车内人员的封锁率随弹目相对距离的变化规律符合

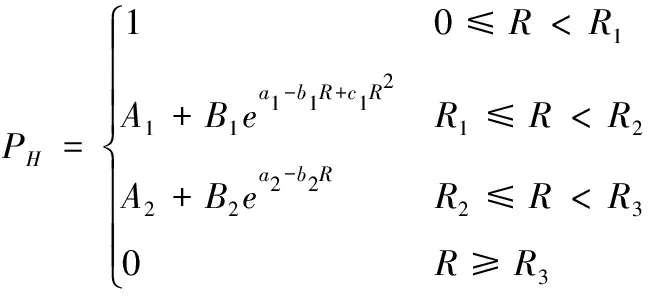
(1)

式(1)中:PH为云爆弹对火箭发射车内有生力量的封锁率;R为弹目相对距离;A1、B1、A2、B2、a1、b1、c1、a2、b2为模型常数;R1、R2、R3为封锁范围分段点。

对于云雾爆轰区外冲击波超压的衰减规律,符合爆炸相似律,有

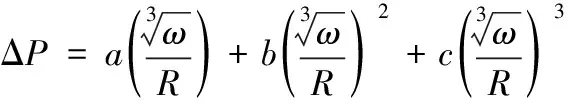
(2)

式(2)中:ΔP为冲击波超压;ω为炸药装药量;R为冲击波传播距离;a、b、c为衰减系数。

考虑到云爆弹分布爆炸,超压衰减缓慢,且实测地面超压受马赫杆的影响。为准确表达云爆剂质量以及冲击波传播距离对地面超压的关系,对式(2)进行修正[16]

(3)

式(3)中:m为云爆剂装药量;AR为TNT当量比,可直接反映各距离R处云爆弹的冲击波超压威力,且满足AR=ωTNT/m。

最终,结合式(1)与式(3),通过最小二乘法,得出式(1)中函数模型常数,获得云爆弹对火箭发射车内有生力量的毁伤评估模型:

(4)

根据式(4)可以直接以车内有生力量死亡为封锁依据,通过云爆弹装药质量以及TNT当量比,直接判断云爆弹在各个弹目距离下对火箭车内有生力量的毁伤效能。

3.5 毁伤评估模型的验证

为验证毁伤评估模型的有效性,以33 kg云爆弹为例,将毁伤评估模型所得结果与地面超压实验数据结论[18]对比,通过分析两者误差进行验证。

首先,基于毁伤评估模型,由33 kg装药云爆弹的TNT当量比以及装药质量,获得该云爆弹对各弹目相对距离火箭发射车内有生力量的封锁率,结果如图11所示。33 kg装药的云爆弹可对11.35 m范围内火箭车目标完全封锁;在11.35～15.46 m范围内,封锁率迅速下降,并在弹目相对距离为15.46 m时,封锁率减为0。

图11 各弹目相对距离下火箭发射车内 有生力量的封锁率

其次,为减小验证计算量,选取图11中不同封锁范围内弹目相对距离为9、12、15、18 m这4个特征工况进行验证。通过对33 kg云爆弹静爆实验数据仿真分析,获得各个工况实际封锁率,并将实验分析结果与毁伤评估模型所得结果进行对比,两者相差在2%左右,证明了毁伤评估模型的有效性和适用性,结果如表10所示。

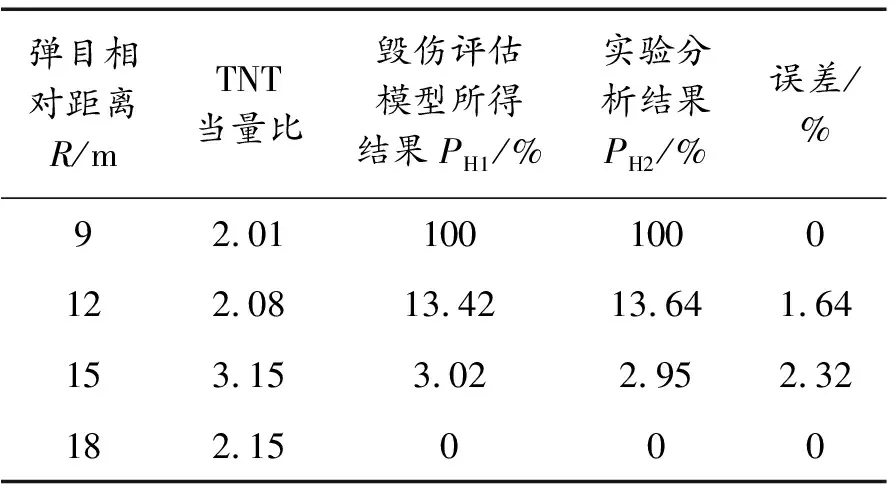
表10 33 kg装药云爆弹对火箭车内人员封锁率计算结果

4 结论

基于云爆弹在地面超压分布场的实测数据,提出一种计算云爆弹在车内所形成超压分布场的数值方法,并验证了该方法的等效性。通过分析不同因素对车内超压分布场的影响,确定了车内超压的分布规律。并结合超压对人员的杀伤判据,采用蒙特卡洛方法,提出了该云爆弹超压效应对火箭发射车内有生力量的毁伤评估模型,得到以下结论:

1) 在同一位置起爆不同等效当量的TNT,以此模拟ZBD-2型云爆弹在对应各弹目相对距离情形中的超压威力。该方法计算所得超压与实验结果两者误差小于10%,可有效模拟云爆弹攻击火箭发射车时的超压效果。

2) 对于云爆弹在火箭发射车内的超压分布场,在其余条件均一致时,跪姿乘员所受超压高于坐姿;在驾驶/指挥室中,副驾驶区域乘员所受超压高于主驾驶区域;在火力控制室中,各区域所受超压一致。

3) 以有生力量全部死亡为标准,基于蒙特卡洛法可得,ZDB-2型云爆弹可成功封锁28 m范围内的火箭发射车;随着弹目相对距离的增加,该云爆弹将逐渐丧失对火力控制二区、一区、主驾驶区以及副驾驶区内人员的封锁能力;直至在弹目距离为36.35 m时,将丧失对火箭发射车的封锁能力。

4) 基于爆炸相似律,提出云爆超压效应对火箭发射车内有生力量的毁伤评估模型。该模型可根据云爆弹装药量及其TNT当量比,确定对各弹目相对距离处车内人员的封锁率,并由33 kg云爆弹实验数据验证了该模型的有效性。