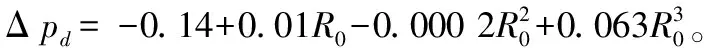两点串联装药爆炸区域增效效果分析

吕中杰,赵开元,王乐阳,刘 彦,黄风雷,黄 宁,杨剑波

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.北京理工大学重庆创新中心, 重庆 401120; 3.中国人民解放军32184部队)

0 引言

串联装药爆炸冲击波威力场的分布规律是扫雷、破障[1]和多点同步爆炸[2]等领域研究的焦点。与单个装药爆炸冲击波传播相比,串联装药爆炸冲击波在发生正面碰撞、交汇作用后,会形成强反射波[3],使得部分爆炸区域出现冲击波区域增效现象。增效区域内冲击波相互作用机理、波形结构、超压分布复杂,揭示串联装药爆炸冲击波相互作用机理及分布规律对扫雷、破障和多点同步爆炸等领域研究有着重要意义。

国内外学者对多点同步起爆进行了大量的研究。一些学者对多点同步爆炸的研究主要集中在多点同步爆炸的毁伤效应相较于同质量单点爆炸的毁伤效果增益上。孟闻远等[4]利用ANSYS/LS-DYNA仿真软件研究了两点水下同步爆炸冲击波对冰体的破坏效应。张世豪等[5]利用AUTODYN软件对多点装药在混凝土中的同步爆炸进行了数值模拟,分别从爆炸应力波和混凝土的毁伤情况对多点爆炸能量聚集效应进行了研究。翟红波等[6]通过设计舰船舱室的等效缩比模型,对双点装药同步内爆炸和单点装药同步内爆炸对缩比舱室的毁伤情况进行了研究。一些学者对多点同步爆炸的研究则是集中在多点同步爆炸的冲击波超压、冲量等特性相较于同质量单点爆炸的增益研究上。美国核防局和Sandia实验室[7-9]研究了多点装药同步和非同步爆炸所形成的冲击波高压峰值相较于单点装药的增益效果。胡宏伟等[10]基于实验,通过改变装药质量组合和布局对多点同步地面爆炸冲击波的增强效应进行了研究。冯海云等[11]研究了两点同步爆炸冲击波场的分布规律及其相对于同质量整体单点爆炸威力的增益效果。

上述研究多为多点同步爆炸在毁伤效果或冲击波特征值相较同质量单点爆炸的增益效果上,然而对于同步爆炸冲击波的传播过程、相互作用以及增效区域的研究没有深入阐述。串联装药爆炸的主要特征是多点同步爆炸所产生的冲击波能够发生相互作用,2个冲击波的汇聚和反射导致了更为复杂的波系结构和冲击波超压场、冲量场的分布。本研究中基于两点装药同步爆炸,设计了不同装药质量及不同装药间距的工况,并开展了对数值模拟结果的超压、冲量衰减规律的试验验证,对两点装药爆炸过程中的相互作用进行了数值模拟,分析了两点装药爆炸冲击波的传播和相互作用过程,得出了典型爆炸区域的入射波超压、反射波超压分布结果,并对增效区域进行了划分。针对不同毁伤阈值的应用场景,得出了装药质量、最佳装药间距与毁伤阈值之间的关系。

1 数值模拟

1.1 计算工况

炸药为圆柱形TNT药柱,长径比为1∶1,采用中心点起爆方式,药柱放置于地面上。计算工况见表1,两点装药爆炸的布局如图1所示。

表1 仿真工况表

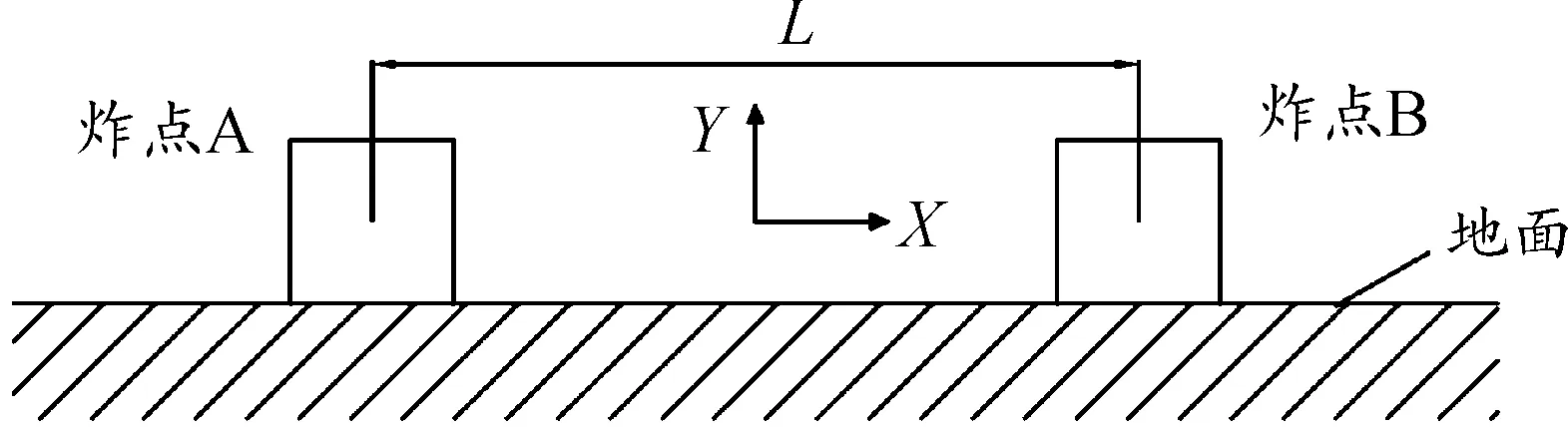
图1 仿真布置示意图

1.2 模型和参数

文献[12-13]认为,用LS-DYNA软件中的无反射边界条件来模拟无限空域时,会造成能量的不守恒,导致在离无反射边界条件越近的空气区域,冲击波的超压历程越背离实际的物理过程,模型尺度与考察范围的比例约为1.2倍,可减小无反射边界的影响。文献[14]指出使用LS-DYNA在进行爆炸冲击波数值模拟时,采用部分建模可以节约大量计算时间的同时不会影响计算精度。为了在提高计算效率的同时保证计算精度,建模时考虑2个部分:一是模型整体以两装药的连线为对称轴,采用1/2建模的方式来缩短计算时间;二是建模尺度应该适当地大于考察范围,消除无反射边界对计算精度的影响。

有限元模型局部放大图如图2所示,整体模型采用1/2建模方式,其中蓝色区域为空气域,米黄色区域为TNT药柱,黑色区域为混凝土地面。计算模型中的空气域为1/2圆柱体,高为2.5 m,半圆面直径为5 m,空气四周设置为无反射边界,TNT与空气域采用ALE多物质组分算法模型。地面为1/2圆柱体,高为0.3 m,半圆面直径为5 m,采用拉格朗日算法模型。TNT、空气域和地面之间采用流固耦合算法来实现2种网格的相互作用。

图2 有限元模型局部放大图

计算过程涉及材料包含空气、TNT和混凝土地面。其中,TNT采用高能炸药材料模型并用 JWL状态方程描述,其表达式为

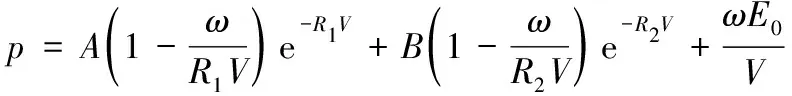
(1)

式(1)中:p为压力;A、B、R1、R2、ω为JWL状态方程参数;V为相对体积;E0为初始内能。相关参数取值如表2所示。表2中:D为炸药的爆速;Pcj为爆压;ρ为炸药密度;V0为初始相对体积。

空气材料选用线性多项式状态方程描述,其表达式为

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(2)

表2 TNT炸药参数

表3 空气参数

混凝土采用*MAT_ CONCRETE_DAMAGE_REL3材料模型。该模型简化材料输入,基于3个剪切破坏面,考虑损伤和应变率的影响,通过输入混凝土无侧限抗压强度、材料密度和泊松比,自动生成其他参数以及状态方程,能够较为准确模拟混凝土在爆炸荷载下的动态响应[15]。相关参数取值如表4所示,表4中,RSIZE为长度单位的转换量(转换成英寸),UCF将当前压力单位转换成磅每平方英寸。

表4 混凝土参数

2 实验验证

为了验证数值模拟模型,选用TNT装药进行实验,装药密度为1.58 g/cm3,长径比为1∶1,质量为75、150 g等2种药柱,实验场地为混凝土地面。实验测试了75 g和150 g单点装药爆炸和药柱质量75 g、装药间距2 m的两点装药爆炸冲击波参数,以此验证所采用计算模型的正确性。实验现场布置图如图3所示。

为了保证两点装药同步爆炸的同时性,实验中采用导爆索将2个TNT药柱连接,使用工业8号雷管对导爆索的中点进行起爆,通过导爆索中传导的爆轰波起爆2个TNT药柱。实验测点布局如图4所示,超压测点位置固定,测点3位于炸点A和炸点B连线的中点处,测点1、2、3、4、5间隔30 cm,测点3、6、7、8、9间隔50 cm。

图3 炸药起爆示意图

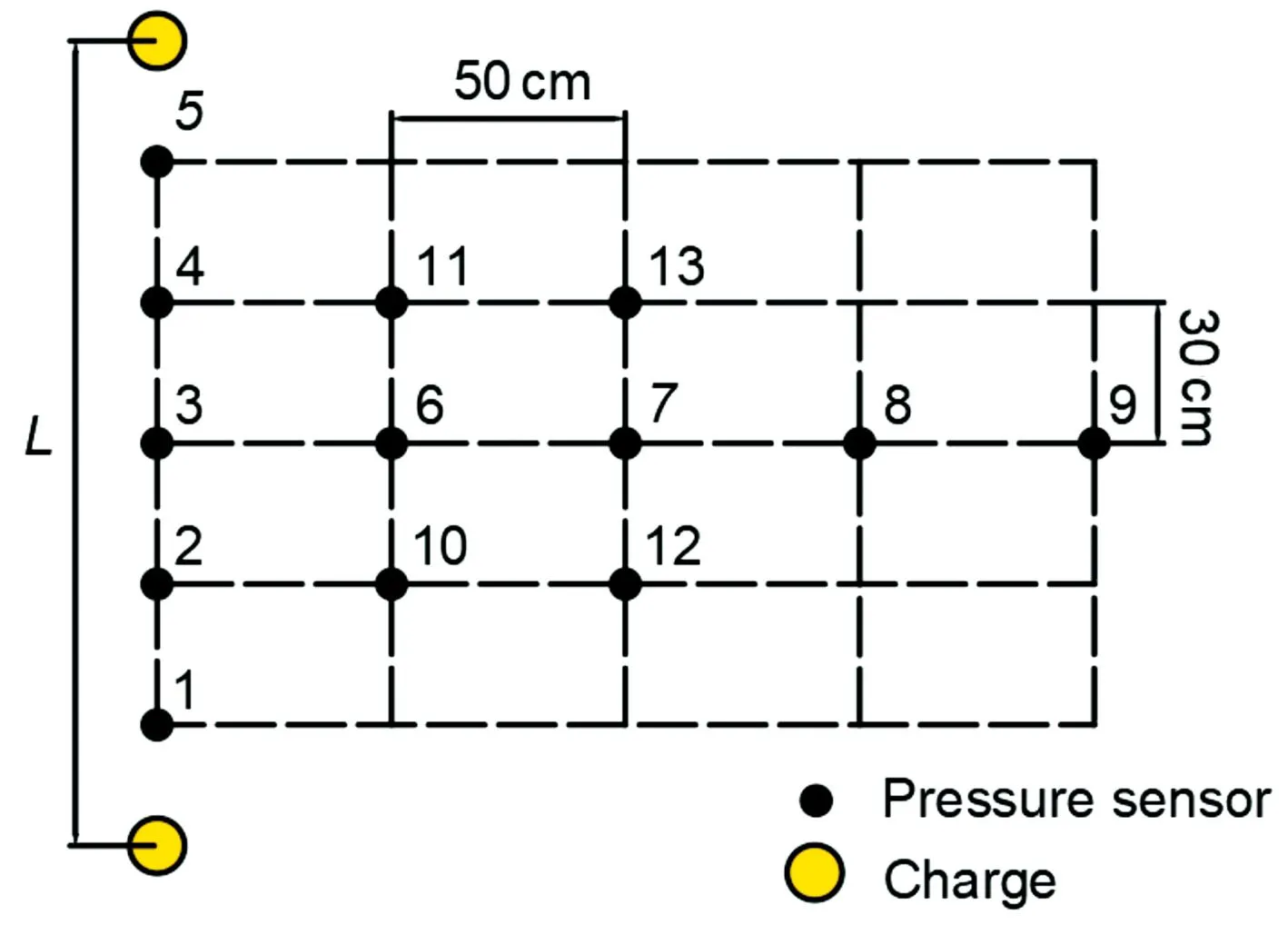
图4 超压测点布置图

3 结果与讨论

3.1 经验计算公式

以往的研究人员基于不同比例距离和装药质量的大量实验数据,分析得到了多种不同的经验公式来预测爆炸冲击波的参数。其中运用较为广泛的有Henrych公式和叶晓华公式。

Henrych公式:

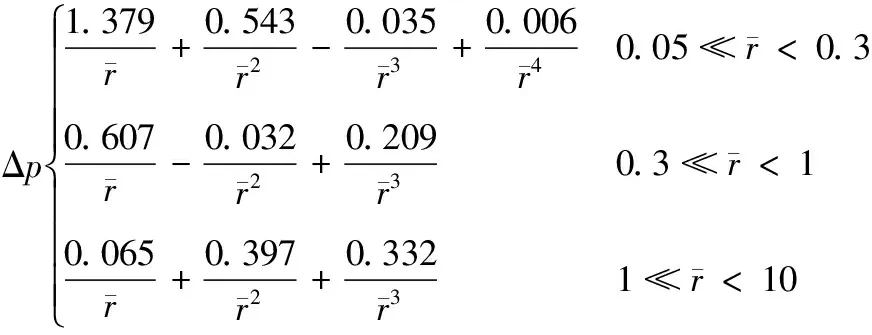
(3)

叶晓华公式:

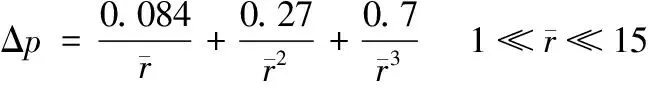
(4)

对于装药地面爆炸,一般对刚性地面以2倍装药量,普通土壤地面以1.8倍装药量代入计算。

3.2 模型参数设置的有效性验证

由图5可看出,冲击波超压的实验值、数值模拟结果与经验公式计算结果在总体衰减趋势上基本保持一致,经验公式计算结果整体高于数值模拟结果和实验值,这是因为临地爆炸时冲击波与地介质之间的相互作用在地介质中产生应力波造成能量损失[15],导致实验测得的冲击波参数较经验公式计算结果偏小。由表5可知,数值模拟结果与实验值在衰减趋势上保持一致且偏差不大于20%。

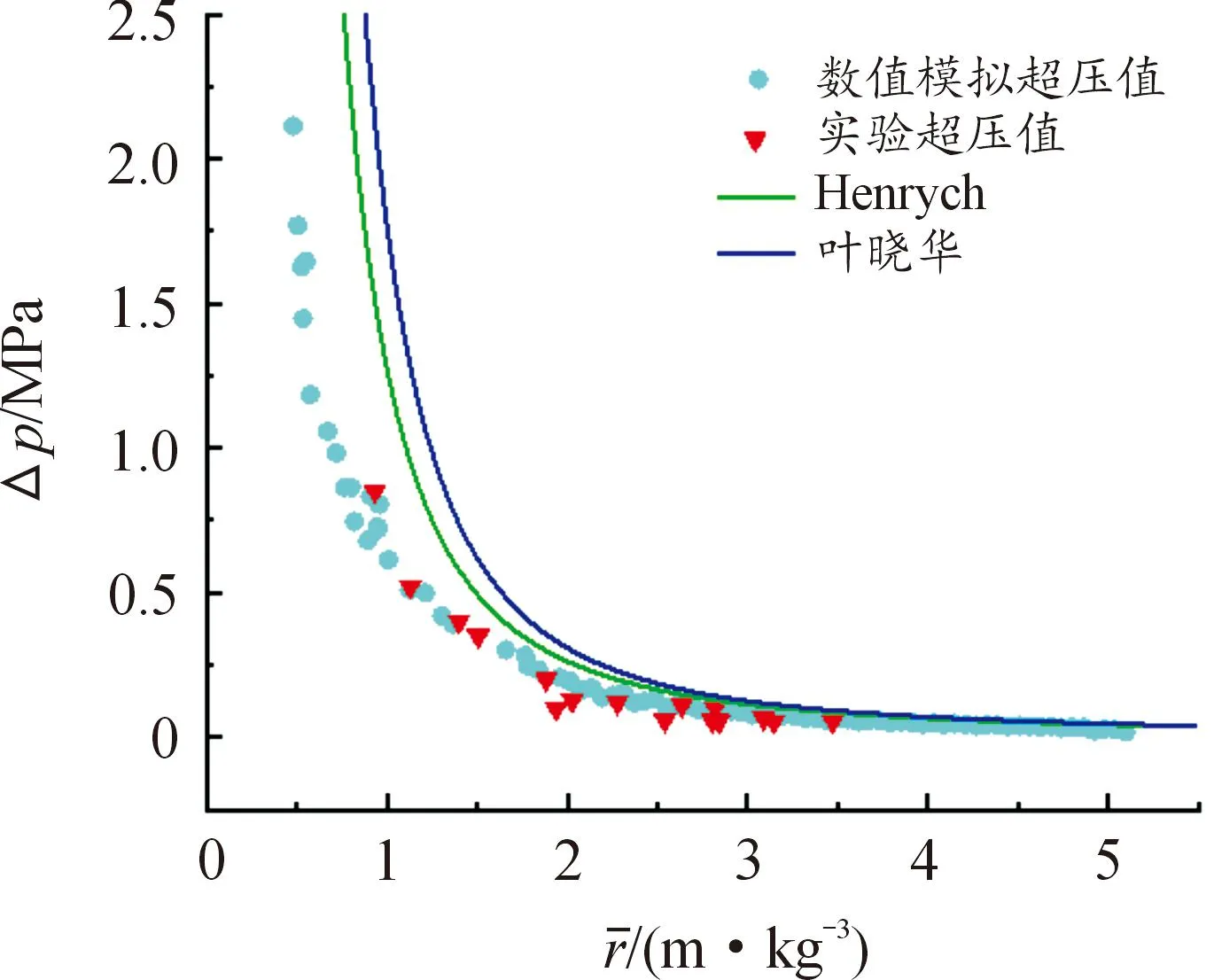
图5 超压-比例距离衰减趋势对比图

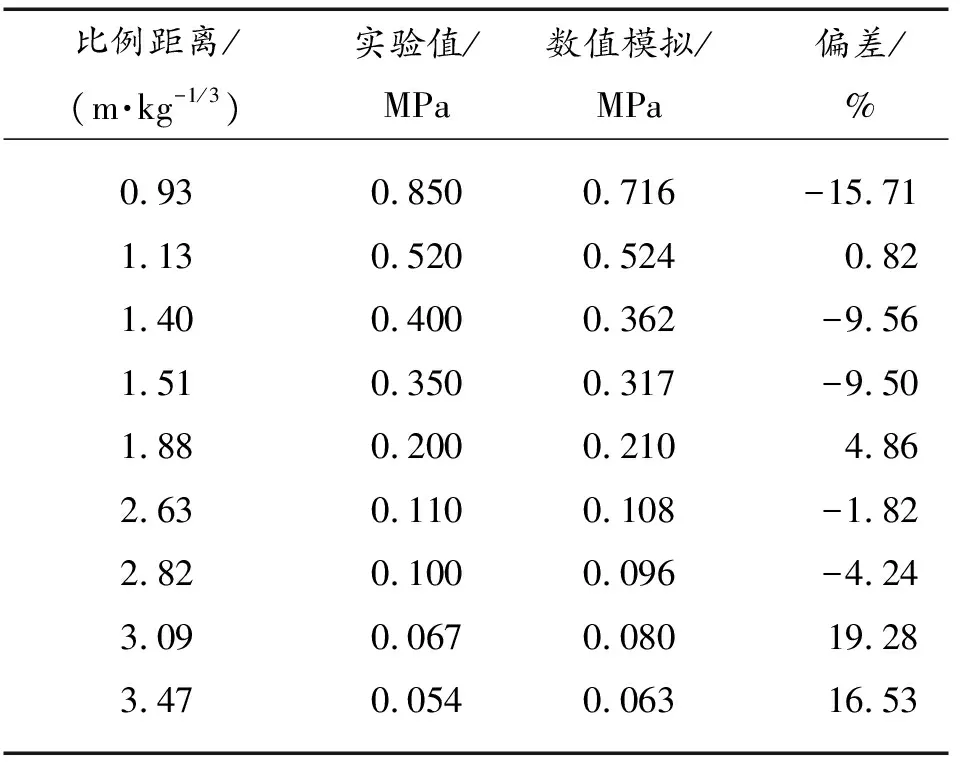
表5 超压实验结果和数值模拟结果对比

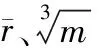
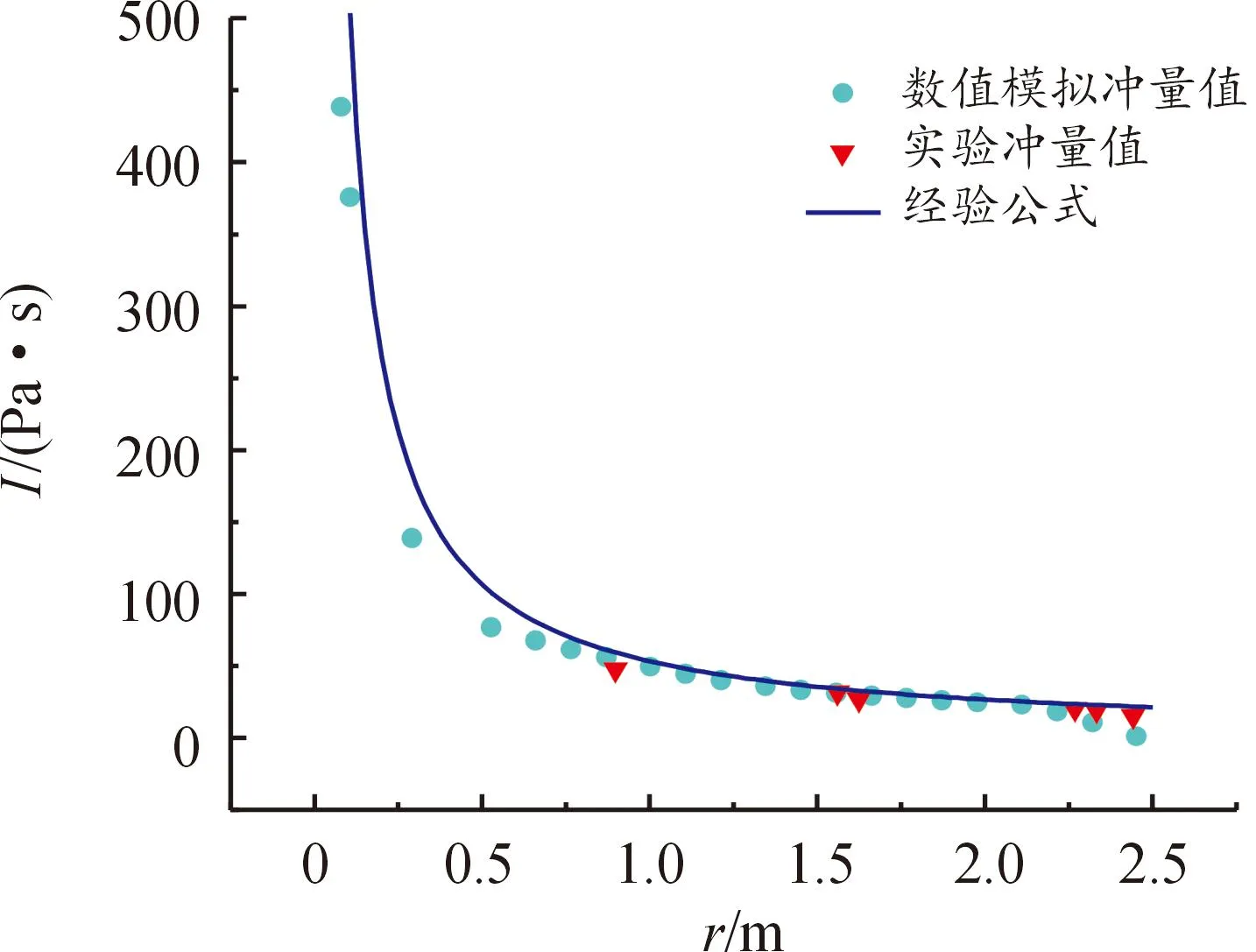
图6 75 g TNT冲量-距离衰减趋势对比图 Fig.6 75 g TNT impulse-distance attenuation trend comparison chart

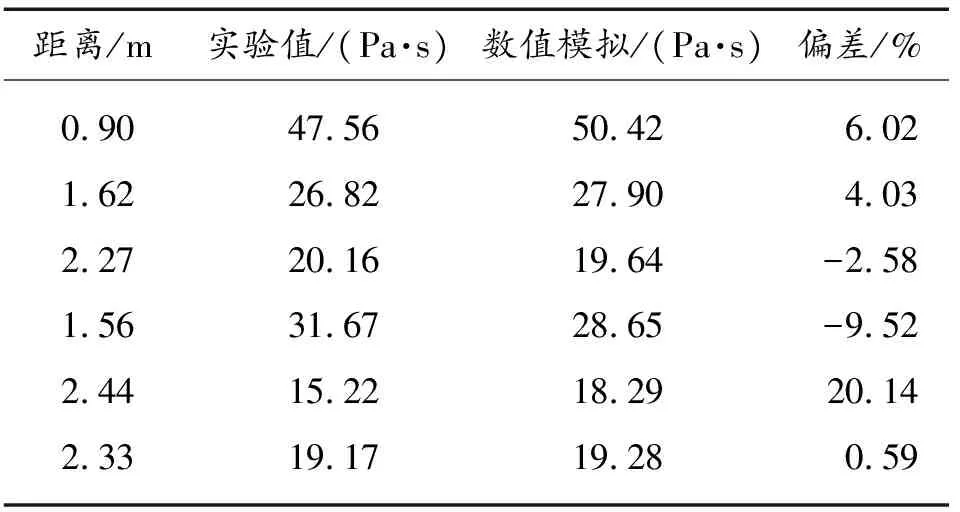
表6 75 g TNT冲量实验结果和数值模拟结果对比

为验证数值模拟在爆炸冲击波在发生叠加后结果的准确性,对两药柱连线上测点的超压值进行对比。选取工况75×2两点装药的数值模拟结果和试验结果的超压值进行对比验证。超压对比结果见表7。

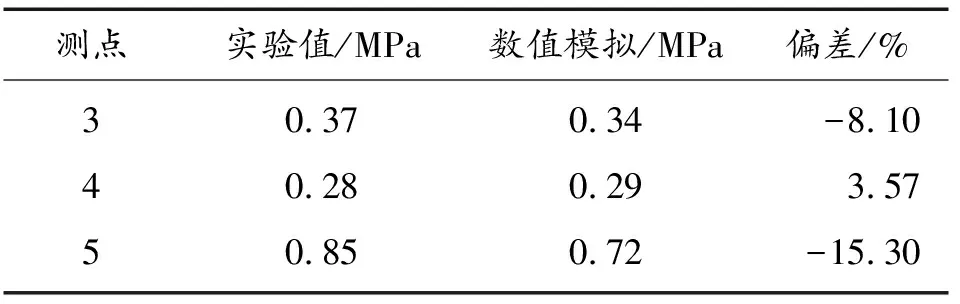
表7 两点装药冲击波参数对比 Table 7 Comparison of shock wave parameters of the two-point charge

综上所述,可以得到数值模拟结果和实验值吻合较好,冲击波超压、冲量在衰减趋势上一致且与经验公式计算结果相近,超压峰值和正压冲量的对比最大误差不超过20%。说明数值模型参数设置有效,得到的计算结果准确可靠。

3.3 两点装药同步爆炸增效区域划分

为探究两点装药爆炸出现区域增效现象的原因,选择75 g×2(药柱质量×个数),装药间距L为2 m工况的数值模拟结果对两点装药爆炸冲击波传播过程及相互作用进行分析。2个冲击波从开始传播到发生相互作用的这段时间中,选取0.7、1.1、1.3、2.3 ms等4个典型时刻的压力等值面,对冲击波的演化过程进行分析,数值模拟结果如图7所示,选取视角为两药柱中点连线的剖面。

图7 压力等值面图

由图7可以看出,2个药柱同步起爆后,在0.7 ms时刻由2个药柱爆炸产生的冲击波各自独立的向外界传播,此时2个冲击波之间互不干扰,此阶段为入射冲击波的独立传播阶段。随着冲击波继续传播,在1.1 ms时刻2个半球形的入射冲击波阵面开始交汇并发生正反射形成2道反射波,此时入射波和反射波叠加形成高压区,随着时间的发展,2个入射冲击波的交汇面积开始增大,交接点开始垂直地面向上移动,在1.3 ms时刻,高压区开始变得狭长,此时由于入射波与反射波的速度方向相反,入射波和反射波开始分离,此阶段为入射冲击波交汇阶段。随着冲击波的继续演化,在2.3 ms时刻反射波和入射波完全分离,此时的反射波开始以入射波交汇区为中点向四周空间独立传播,此阶段为反射冲击波传播阶段。

通过对两点装药爆炸冲击波传播过程及相互作用分析可以得到,两点装药爆炸区域出现冲击波超压区域增效现象是因为2个药柱爆炸产生的入射波在交汇区域发生正反射形成反射波,入射波和反射波在交汇区域的叠加造成超压峰值的增加。下面对两点装药中点连线上的爆炸冲击波超压进行分析,以两点装药连线的中点作为横坐标原点,建立两点装药冲击波超压和距离之间的关系,增效区域划分如图8所示。

图8中,黑线代表冲击波独立传播阶段的特征,在此距离内,冲击波的衰减趋势与单点装药爆炸冲击波的衰减趋势相同。红线代表入射冲击波交汇阶段和反射冲击波传播阶段,通过与单点装药爆炸冲击波超压峰值对比,将两点装药爆炸增效区域划分为3个部分。图8中红线与蓝线相交的点是两点装药反射波超压值与单点装药入射波超压值相等的点,交点横坐标为0.1 m和-0.1 m。两点装药反射波超压值整体大于单点装药入射波超压值的区域为增效明显区(坐标区间(-0.1 m,0.1 m)),此区域冲击波超压的最高峰值达到0.34 MPa,相较于相同位置处单点爆炸冲击波超压峰值0.13 MPa提高了2.6倍。两点装药反射波超压值整体小于单点装药入射波超压值且高于0.03 MPa的区域为增效过渡区(坐标区间(-0.21 m,-0.1 m)∪(0.1 m,0.21 m)),在此区域内,反射波仍存在,但反射波超压峰值已经低于相同距离处单点装药爆炸入射波的超压峰值。反射波超压值衰减至低于0.03 MPa是增效不显区(坐标区间(-0.6 m,-0.21 m)∪(0.21 m,0.6 m)),在此区域反射波的超压值衰减到接近0 MPa,与相同距离处单点装药入射波超压峰值相比影响可以忽略。

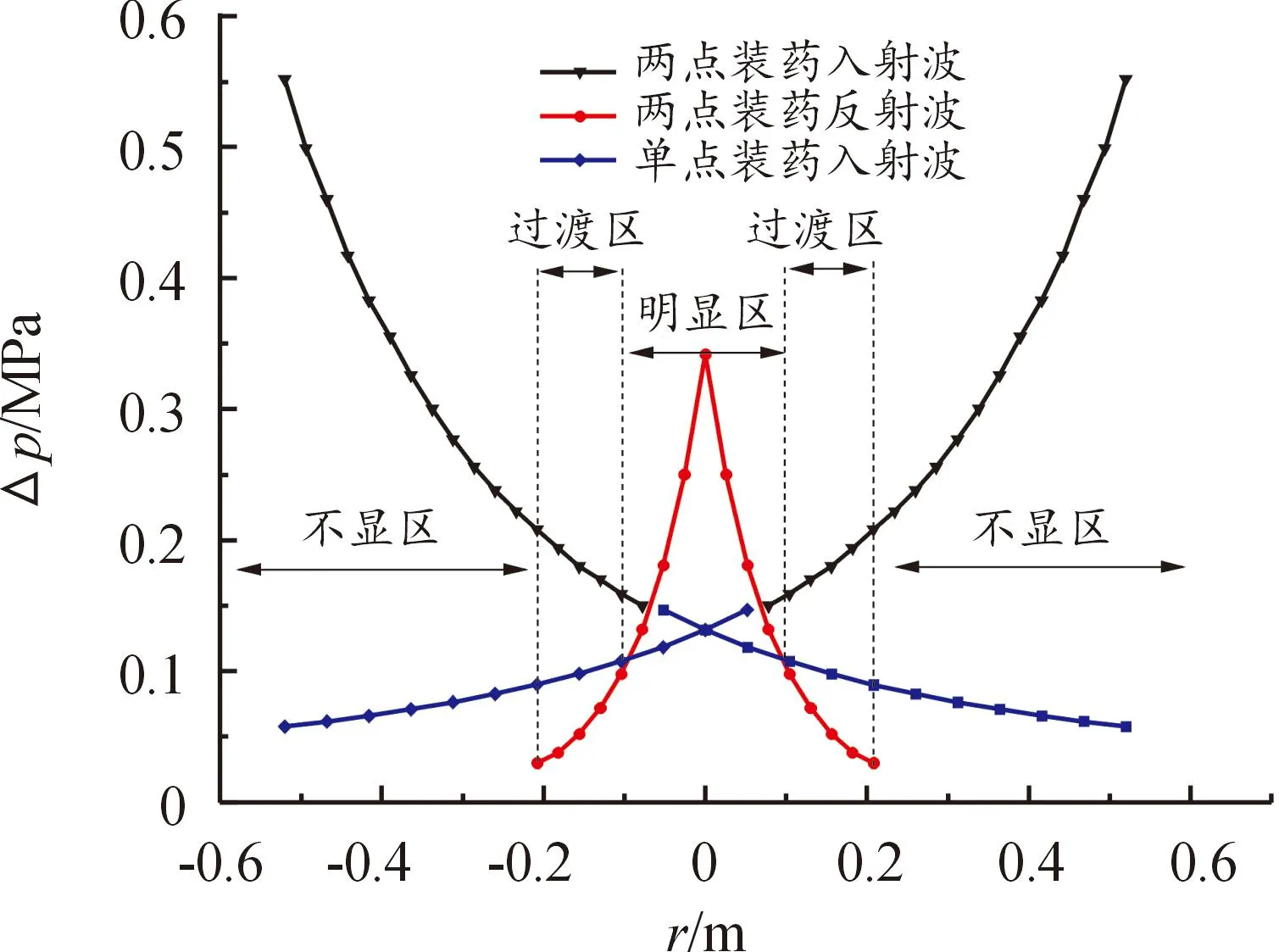
图8 增效区域划分

3.4 装药间距对有效作用区域面积的影响规律

以给定的冲击波超压Δpd为毁伤阈值基准,单点装药爆炸冲击波的有效作用区域是以爆炸中心为圆心,以能达到超压Δpd的最远距离为半径rd的圆包围起来的区域。如图9所示,在两点装药爆炸冲击波互不干涉的情况下,两点装药爆炸冲击波的有效作用区域为2个半径为rd的圆相交的区域。在冲击波的相互作用的情况下,冲击波交汇区域附近存在着超压增效现象,因此冲击波相互作用下的有效作用区域面积相较于冲击波互不干涉的情况有着区域增效现象。

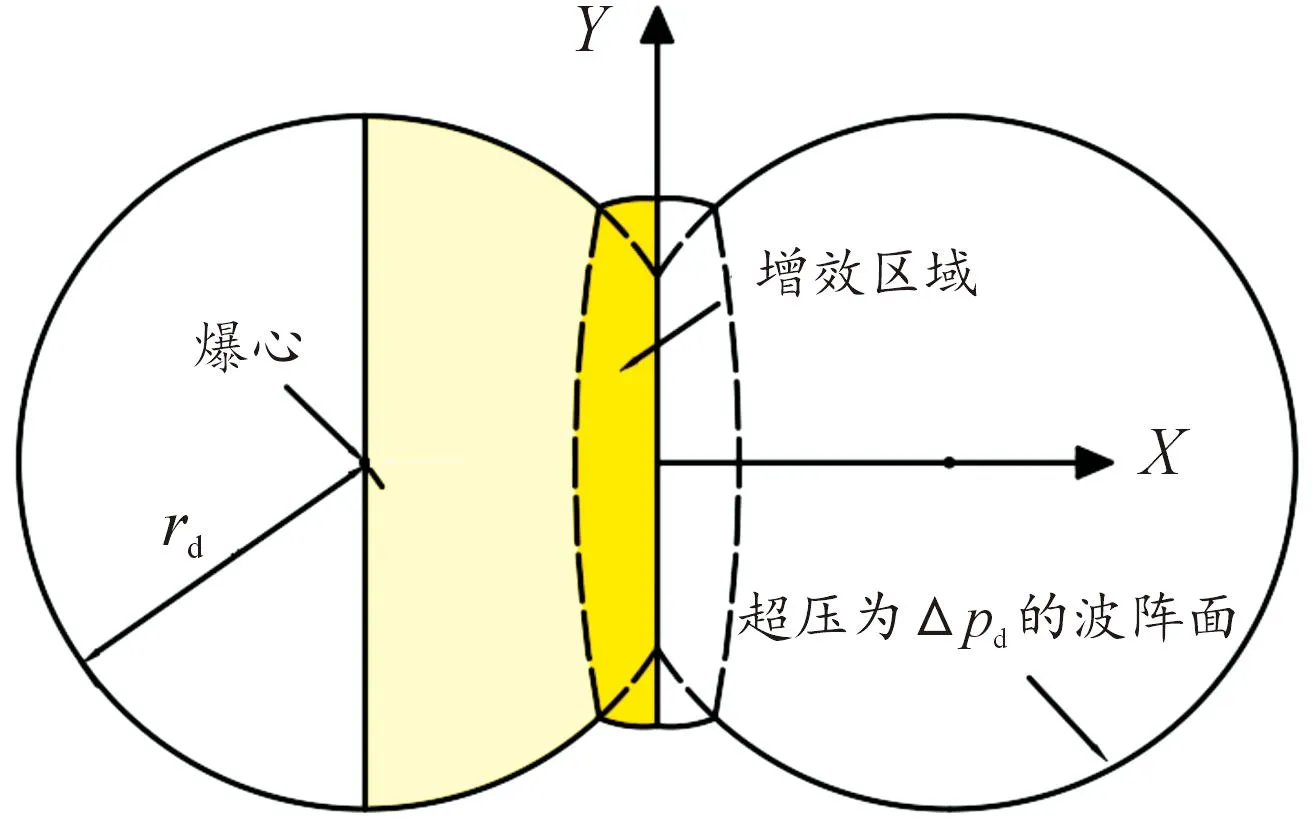
图9 两点装药冲击波有效作用区域

总质量150 g装药工况选取Δpd为0.05、0.06、0.09 MPa和0.12 MPa的毁伤阈值,总质量300 g装药工况选取Δpd为0.08、0.10、0.14、0.18、0.23 MPa的毁伤阈值。得到冲击波有效作用区域面积Sd随装药间距L的变化关系如图10、图11所示。

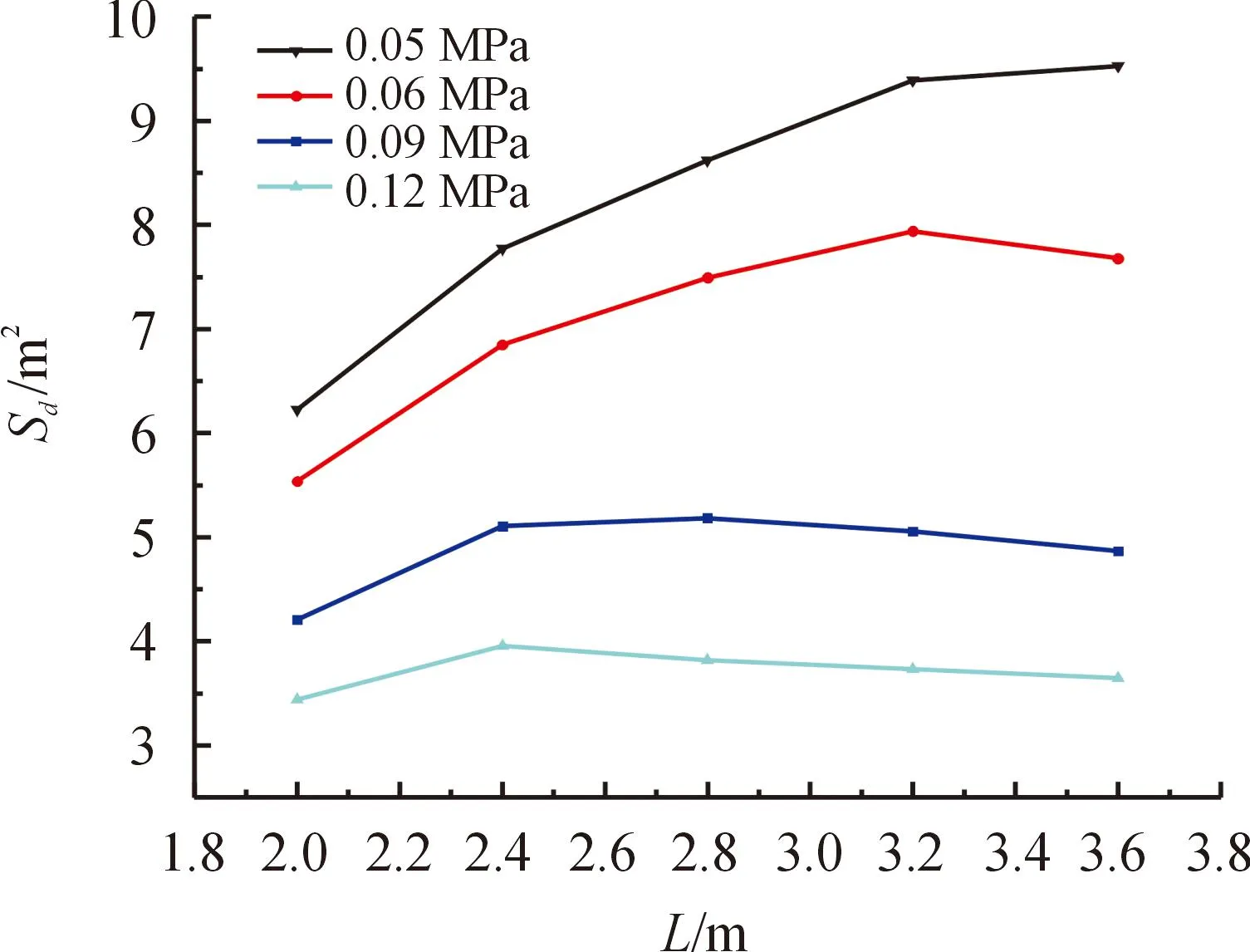
图10 150 g装药有效作用区域面积随装药间距的变化

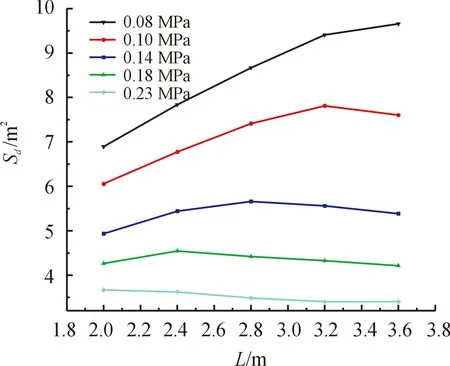
图11 300 g装药有效作用区域面积随装药间距的变化

选择总质量150 g装药工况得到的结果进行分析。从图10中可以看到,装药间距L的变化对两点装药爆炸冲击波的有效作用区域面积有着明显的影响。对于0.05、0.06、0.09、0.12 MPa的毁伤阈值来说,总质量150 g两点装药最佳的有效作用区域面积对应的装药间距L分别为3.6、3.2、2.8 m和2.4 m,随着毁伤阈值的提高,最佳有效作用区域面积对应的装药间距随之减小。总体来看,对于不同的毁伤阈值,有效作用区域面积随着装药间距L的增加,出现先增大后下降的趋势,对于指定的装药质量,指定的毁伤阈值来说,存在着一个最佳的装药间距L0使有效作用区域面积达到最大。

3.5 不同毁伤阈值的最佳装药间距工程计算模型

表8 不同毁伤阈值的最佳装药间距结果

图12 毁伤阈值和装药质量、最佳装药间距的关系

基于爆炸相似律,毁伤阈值Δpd和最佳装药间距与装药质量立方根的比值R0存在函数关系。设函数关系为:

Δpd=f(R0)

(5)

将式(5)进行泰勒展开,精度保留三次项得到:

Δpd=A0+A1R0+A2(R0)2+A3(R0)3

(6)

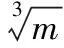
4 结论

1) 通过数值模拟和装药间距2 m的两点装药爆炸实验,验证了数值模拟结果与实验数据结果吻合较好,证明了本文所采用计算模型的有效。

2) 通过对两点装药爆炸冲击波的传播过程进行了分析,根据冲击波叠加反射的特性,得到了两点装药爆炸冲击波增效区域划分结果,结果表明,在冲击波相互作用的影响下,爆炸区域出现增效明显区、增效过渡区和增效不显区。

3) 对于指定的超压毁伤阈值,装药质量,总存在一个最佳装药间距使得冲击波有效作用区域面积达到最大。