双重响应异常约束的无人机目标跟踪

郭伟， 林畅， 王春艳， 杨涵西， 才海亮

（辽宁工程技术大学 软件学院， 辽宁 葫芦岛 125105）

1 引言

随着无人机行业的兴起，无人机因其外形小巧、运动灵活且方便操控等特点，与目标跟踪技术的结合使其在普通居民生活、军事活动以及科学研究等多个领域得到越来越广泛的应用［1-2］，如空中监控、基础设施巡逻、抢险救灾、侦察敌情等。与普通的跟踪场景相比，无人机目标跟踪面临着更艰巨的挑战，如恶劣的外部挑战、复杂环境中的机动飞行等。

相关滤波类目标跟踪算法因其跟踪速度快、跟踪性能好而得到了广泛应用［3-5］。Bolme等人［6］在2010年提出了最小输出误差平方和（MOSSE）跟踪算法，并将相关滤波算法应用于目标跟踪领域。Li等人［7］将时间正则化引入空间正则化相关滤波算法，为了提高算法跟踪精度和速度，建立了相邻两帧滤波器之间的关系，并提出了交替方向乘子法（ADMM）求解方程组。Huang等人［8］利用前后两帧响应图的全局变化情况检测跟踪过程中的异常情况，避免滤波器错误学习过多的背景信息，能有效解决边界效应以及抑制畸变。Li等人［9］提出了一种在线自动自适应学习方法，能够自动学习和调整预定义参数，在多个无人机跟踪任务测试中均达到最优效果。Fu等人［10］将显著性检测方法融入到滤波器训练中，并利用了双重正则化（DRCF）突出了对象外观并取得较好的实验结果。Lin等人［11］提出了一种新的双向不协调感知相关滤波器，将响应的双向不一致误差集成到滤波器中，可以有效地学习外观的变化并抑制不一致误差。王海军等人［12］根据前后帧之间的响应差和相关滤波器的变化建立双重约束的目标函数，能够有效跟踪无人机目标。由此可知，利用响应变化可以有效约束外观变化。在无人机航拍的复杂场景下，实现鲁棒、准确和实时的跟踪是一项非常具有挑战性的任务。

本文提出一种双重响应异常约束的无人机目标跟踪算法（DRACF）。通过计算局部响应变化和全局响应峰值旁瓣比在线动态更新空间正则化参数，确保空间一致性；采用异常峰值判断机制，评估当前帧次峰值所带来的影响，动态更新时间正则化参数，以适应复杂场景变化，解决跟踪漂移问题，进一步抑制异常发生。目标函数通过交替方向乘子迭代求解最优解。将DRACF算法与原算法在多个主流的无人机数据集上进行对比，评估实验结果。

2 时空正则化相关滤波方法

在过去，所有目标跟踪算法都是在时域中处理的。由于其求解过程中需要进行复杂的矩阵求逆运算，因此需要大量的计算量和实时性能，基于相关滤波的目标跟踪方法将计算转换到频域，利用循环矩阵在频域可对角化的特性，使运算量大为降低，运算效率明显加快。为便于了解无人机平台基于相关滤波类目标跟踪算法的跟踪原理，给出一般跟踪结构图如图1所示。

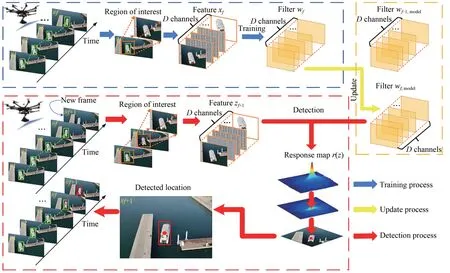
图1 无人机平台基于相关滤波类方法的一般跟踪结构Fig.1 General tracking structure of UAV platform based on correlation filtering class method

基于时空正则化相关滤波（STRCF）［13］目标跟踪算法以相关滤波理论为基础，主要思想源于在线被动攻击学习算法（PA）［14］以及空间约束相关滤波（SRDCF）［4］目标跟踪算法，将时间正则化方法与SRDCF相融合，得到了时空正则化相关滤波器，能够有效降低边界效应的影响，在外观变化较大的情况下比SRDCF具有更强的鲁棒性。STRCF算法的目标函数如式（1）所示：

其中：y为目标响应函数，D表示总通道数，xd为当前帧中提取到的样本，d表示特征通道索引，w为空间权重矩阵，μ为时间权重因子。

相比SRDCF算法，由于引入了时间正则项，在训练阶段不需要用到之前所有T帧的信息，从而大幅减少了训练所需的内存，提高了计算速度，达到实时跟踪的效果（30帧/s）。尽管STRCF取得了令人满意的性能，但它仍然存在两个局限性：（1）时间正则化参数设置为常数，不具有通用性，在很多视频序列中不能获得理想的跟踪结果；（2）固定空间正则化不能有效处理跟踪场景中不可预见的外观变化问题。

3 算法描述

3.1 局部响应变化约束

在目标跟踪过程中，由于背景环境、边缘效应和物体外形改变等因素的干扰，使所产生的响应图在特定的地方发生畸变或异常，而响应图提供的信息能从某种角度反应出当前帧的外观模型与实际目标之间的相似性［15］。不同状态下响应图的变化情况如图2所示。

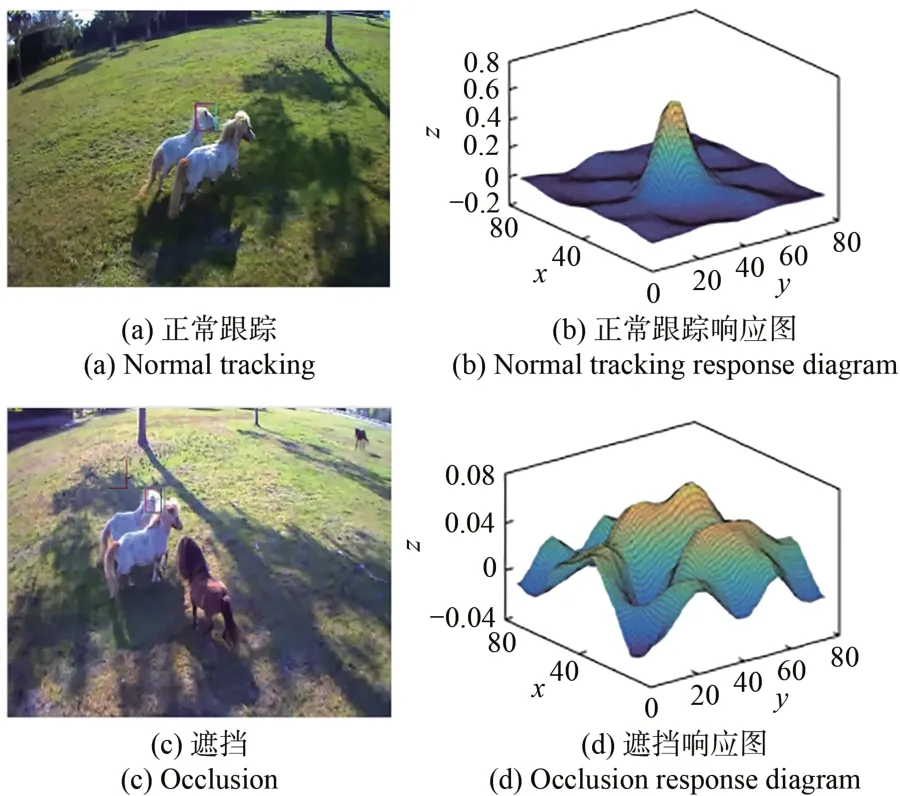
图2 跟踪状态及其对应的响应图Fig.2 Tracking states and corresponding response maps

本文利用前后两帧全局响应偏差构造局部响应变化向量，以此作为判断目标跟踪过程中前后两帧图像的响应图变化剧烈程度的依据。当前后两帧响应图剧烈改变时，这一区间的可靠性降低。

我们将局部响应变化向量Δi定义为：

式中：Rt[ψΛ]i为当前样本生成的响应图为上一帧样本生成的响应图；Rt表示响应图R中的第t个元素；η为学习率，设置为8。

在此基础上，通过局部响应变化向量，以及由视频第一帧中获取到的目标大小信息构建的裁剪矩阵PT，构建了如式（3）所示的空间正则项

μ继承STRCF以减轻边界效应，正则化参数δ为常数。在实际运用中，当跟踪的可信度较高时，目标的空间变化范围相对较小。与此对应的是，在快速运动且视角变化较大的情况下，其跟踪可靠性较差。为实现基于可信程度的实时校正，本文提出以峰值旁瓣比法（Peak to Sidelobe Ratio，PSR）为衡量跟踪系统可靠性的指标，实现对正则参数的实时动态计算和更新。峰值旁瓣比的定义如式（4）所示：

式中：Rt最大值用max函数求解，ωt为特征响应图的均值，σt为特征响应图的方差。图3为coke序列的峰值旁瓣比变化情况，当出现遮挡或模糊时，峰值旁瓣比低于20，判断为不可靠。当算法能够精确跟踪定位时，峰值旁瓣比较大，反之峰值旁瓣比很小，所以用峰值旁瓣比自适应地计算空间正则化系数δ：

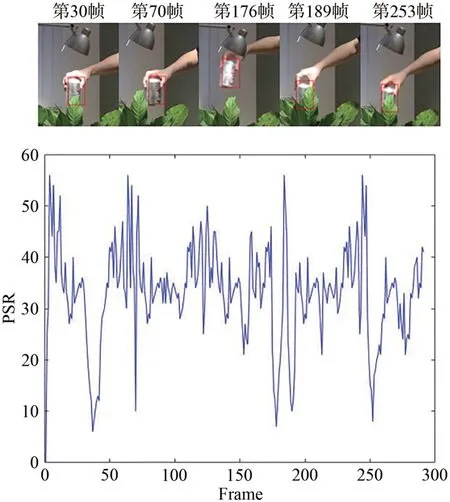
图3 峰值旁瓣比随跟踪变化图Fig.3 Variation of peak sidelobe ratio with tracking

式中：β为学习率，Pt为当前帧的峰值旁瓣比。

3.2 次峰响应变化约束

在STRCF算法中的时间正则项的超参数是固定的，无法自适应复杂的跟踪场景变化。当跟踪目标物体由于快速运动、遮挡、形变、相机旋转等因素造成目标外观发生明显变化时，模型因鲁棒性较差易导致跟踪漂移。

无人机目标跟踪场景复杂多变，当遇到严重的环境变化、类似的物体干扰和其他不利条件时，响应图将严重波动，同时出现多个峰值，如图4所示。对跟踪目标而言，威胁最大的将在响应图中体现为次峰值，图5为响应异常峰值变化情况。这里我们定义一个衡量系数Mk，用以衡量威胁最大的子峰值对当前帧影响的严重性：

图4 目标不同状态时响应峰值变化Fig.4 Response peak changed with the target in different states

图5 响应异常时峰值变化图Fig.5 Peak values change when response is abnormal

其中：R表示搜索区域中的响应图，k表示第k帧，是R中的最大值，ψ表示一个二进制矩阵以显示响应图中的子峰，T定义为：

式中：ν表示T中的权重，ℓ表示距离的影响程度，实验中ν取值为1，ℓ取值为0.2，这两个参数都是预先定义的；d(i，j)表示第i行和第j列的点到矩阵中心的距离，距离中心越远，T值越低；由于响应图的中心峰会影响子峰的搜索，因此中心区域的阈值为dmin，权重设置为0。

最后将得到的Mk融合到时间正则项超参数θt，计算公式如式（8）所示：

其中，υ为经验值，实验中取16。通过动态更新时间正则项参数，将异常影响降到最低，进而使跟踪器更加鲁棒。

3.3 模型更新

在之前的大部分跟踪方法中都使用了固定的学习率，在每帧后都会对滤波器模型进行更新。在目标定位后，会将其作为一个默认的状态，然后在新的目标位置进行新一轮的建模训练并用来对其进行更新［16］。但是，由于现实环境中存在遮挡、背景杂波等因素，由于预测误差，使得被检测到的对象盒中存在一些受影响的数据，因此，若对其进行直接的更新，将会造成对其进行建模的“污染”，进而造成“漂移”的结果。所以，必须选取适当的准则对其进行评价。Wang等［17］提出平均峰值相关能量（Average Peak Correlation Energy，APCE）指标，通过响应图峰值分布情况判别滤波器跟踪状态，即

其中，Fmax、Fmin、Fω，h分别为响应最高、最低和(ω，h)位置的响应值。当目标跟踪正常时，生成的响应图为单峰且计算得到的APCE的数值较大；当目标出现遮挡等异常性情况时，生成的响应图中出现多个不同的波峰且计算得到的APCE数值较小。仅利用最大峰值判据目标的位置和滤波器的更新容易引起目标的漂移甚至丢失。因此，当最大值和APCE值均以一定比例大于前面帧的均值时，可判定当前可以进行模型更新操作；否则，将保持上一帧的跟踪模型，停止更新。在第t帧时，跟踪模型的更新条件按照如下约束：

其中：APCEt，分别表示第i帧响应的平均峰值相关能量和最大响应值，比例阈值ζ1、ζ2为0～1之间的常数。

本文模型更新阶段采用如下方式：

3.4 双重响应异常约束的无人机目标跟踪

DRACF算法以STRCF为基准算法，引入峰值旁瓣比和次峰响应比双重响应异常约束机制，动态更新时空正则项参数，能够有效达到抑制异常准确跟踪的目的，目标函数如式（12）所示：

式中：K为样本特征通道数为空间正则化参数，θt为时间正则项超参数。

类似于STRCF算法的解法，在该方法中，采用了一个附加的变量q，将方程式转换为增广拉格朗日型，然后用ADMM的方法求出：

采用ADMM方法，将拉格朗日形式问题分成多个子问题：

对公式（15）、（16）、（17）进行迭代法的最优值求解。

4 实验与结果分析

4.1 实验环境及参数设置

本文使用的计算机操作系统为Window10，CPU为英特尔i7-10750H，频率为2.60 GHz，内存大小为16 GB。编程软件为MATLAB R2018b。参数设置：局部响应变化学习率η=8，空间正则化系数δ的学习率β=0.3，模型更新阶段学习率α=0.02，ADMM的迭代次数为3，其余参数设置与STRCF相同。

为检验DRACF算法性能，选取近几年优秀的基于相关滤波的目标跟踪算法在3个流行的无人机跟踪数据库UAV123［18］、UAV20L［9］、DTB70［19］上进行仿真实验，并利用benchmark平台与KCF、DSST、SAMF、SRDCF、STRCF、AutoTrack、ARCF这7种算法进行实验并对比分析（表1），对比算法的参数与原文一致。

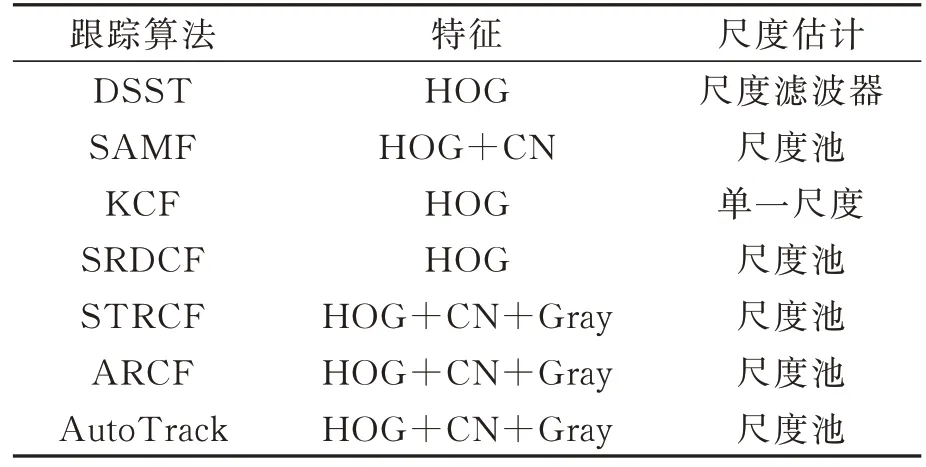
表1 与本文对比的算法Tab.1 Algorithms compared with that in this paper

4.2 数据集及评估标准

UAV123数据集是一个用于低空无人机目标跟踪的测试基准，包括103个专业级无人机拍摄的视频序列，12个小型低成本无人机拍摄的视频序列以及8个虚拟的合成视频序列，共123个视频序列，包含各种不同场景和不同跟踪目标，是无人机目标跟踪领域的代表性数据集之一。有12种挑战属性，分别是尺度变化（SV）、纵横比变化（ARC）、低分辨率（LR）、快速运动（FM）、完全遮挡（FOC）、部分遮挡（POC）、超出视野（OV）、背景杂波（BC）、光照变化（IV）、视角变化（VC）、相机运动（CM）和相似物体（SOB）。UAV20L是UAV123的一个子集，专为长期跟踪而设计，包括20个最长的序列。DTB70数据是一个高多样性无人机航拍数据集，该数据集包含70个视频序列，平均时长7 s，高空环境复杂多样，为短时彩色视频，主要关注相机运动场景下人和车辆的跟踪。

为了评估跟踪算法的跟踪性能，本文采取的评估方式为一次跟踪评估（OPE），即所有视频只跟踪一次。实验中采用OTB-2015测试数据集中两种通用评估方法即跟踪精确度图（Precision Plots）和跟踪成功率图（Success Plots），作为定量评价标准。精确度图显示了阈值在一定范围内的平均精度，本文中阈值取20。成功率图表示阈值在一定范围内的重叠率精度，由曲线下的面积（AUC）评估跟踪器性能。

4.3 实验结果分析

4.3.1 定量分析

图6展示了8种对比算法在数据集UAV123上的距离精度和成功率。图7展示了8种对比算法在UAV20L数据集上的距离精度和成功率。由结果可知，本文算法在数据集UAV123和UAV20L上的表现相对于近几年的优秀算法都是较优的。

图6 UAV123数据集的测试结果Fig.6 Test results of UAV123 dataset

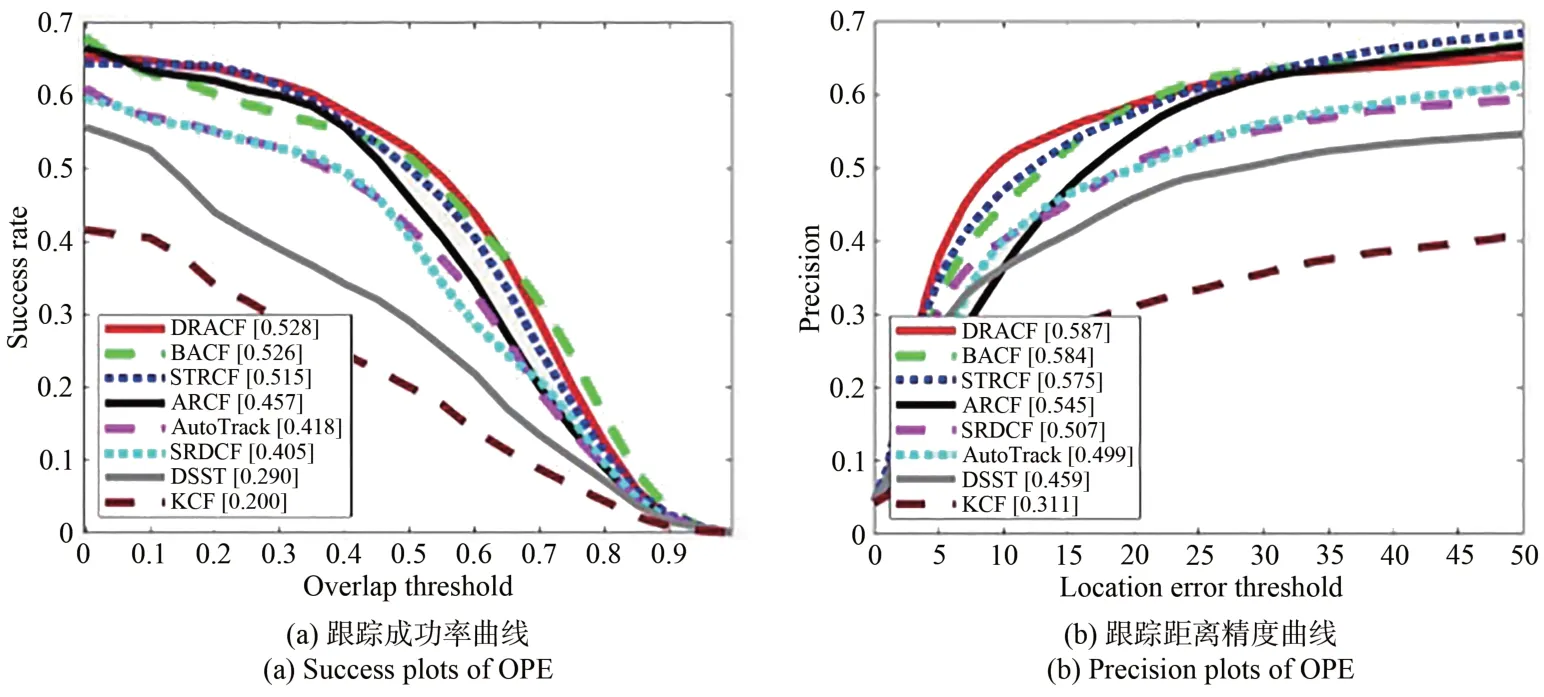
图7 UAV20L数据集的测试结果Fig.7 Test results of UAV20L dataset

DRACF算法在数据集UAV123的距离精度和成功率分别达到71.7%和60.0%，在数据集UAV20L的距离精度和成功率分别达到58.7%和52.8%，精确度和成功率均排名第一，在长时间的跟踪任务中表现优异。图8为本文算法与7种对比算法在数据集UAV123中遮挡、尺度变化、视点变化、相机运动4种属性场景下的成功率曲线图。

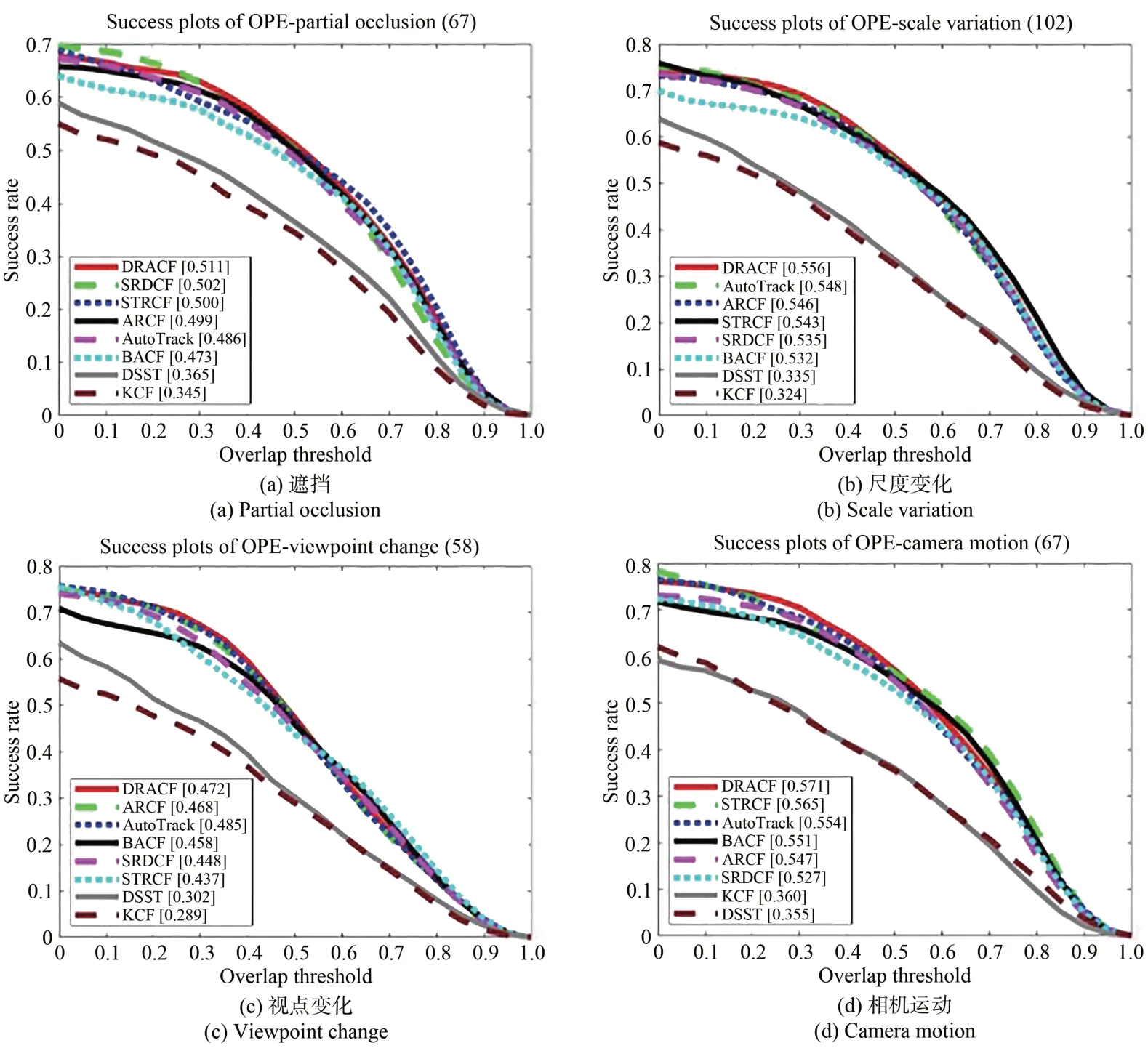
图8 在UAV123数据集中遮挡、尺度变化、视点变化、相机运动属性的成功率曲线。Fig.8 Success rate curves of partial occlusion， scale change， viewpoint change and camera motion attribute in UAV123 dataset.

由实验结果可知，DRACF算法在遮挡、尺度变化、视点变化、相机运动属性的视频序列上均表现良好，优于其他7种对比算法。在UAV123航拍数据集上的出色表现验证了DRACF算法在实际无人机系统上完成目标跟踪抗遮挡、应对目标尺度变化及视点变化等挑战时具有优良的性能。在数据集DTB70的距离精度和成功率分别达到66.7%和52.9%，相对于基准算法STRCF，成功率提升了4.4%、距离精度提升了1.8%。图9为DRACF算法与7种对比算法在数据集DTB70中背景杂波属性场景下的成功率曲线图和精确度曲线图。在背景杂波场景下，相比于同类型的ARCF和AutoTrack算法，DRACF的成功率与精确度均为最高；与基准算法STRCF相比，成功率提升了10.2%。DTB70数据集中的视频序列环境复杂多样，实验结果表明DRACF算法有较好的抑制异常能力。

图9 DTB70数据集中背景杂波属性的距离精度曲线图和成功率曲线图Fig.9 Range accuracy curves and success rate curves of background clutter attribute in DTB70 dataset

为了更加直观地对比DRACF算法与对比算法在各属性下的跟踪效果，表2列出了这8种算法在UAV123数据集上12种视频属性下的跟踪成功率。

表2 8种跟踪算法在各属性序列上的成功率得分Tab.2 Success rate scores of 8 tracking algorithms on each attribute sequence

4.3.2 定性分析

为了更加直观地分析DRACF算法的跟踪性能，将本文算法与SRDCF、STRCF、AutoTrack、ARCF等4种算法在3个具有挑战性的视频序列对比跟踪结果。

图10（a）为DTB70数据集的horse图像序列中的部分关键图像帧的跟踪结果，视频图像包括部分遮挡和完全遮挡的挑战。在开始阶段，无人机低空飞行，目标周围没有障碍物没有发生遮挡现象，所有算法均能够成功跟踪目标；第53～60帧，目标发生了部分遮挡，AutoTrack和ARCF都有不同程度的跟踪误差；第67～70帧，目标发生了完全遮挡，此时STRCF、AutoTrack、ARCF算法跟踪完全失败；第80～126帧，目标脱离遮挡后DRACF算法和SRDCF、STRCF跟踪依旧相对成功，但是STRCF相较于DRACF算法也存在跟踪误差。因此本文采用双重响应异常约束策略，防止其进行错误的更新从而使跟踪失败。

图10 5种算法在3个视频序列的跟踪结果比较Fig.10 Comparison of tracking results of 5 algorithms in 3 video sequences

图10（b）为DTB70数据集的RcCar9图像序列中的部分关键图像帧的跟踪结果，视频图像包括视角变化、快速运动、目标旋转和目标模糊等挑战。视频开始，小车沿直线运行，所有算法均能够成功跟踪目标；第10～45帧，目标小车完成第一次转弯，无人机视角和目标外观均发生变化，SRDCF算法跟踪完全失败；第89～124帧，目标小车进入颠簸路段，此时目标模糊且速度快，因而5种算法均发生不同程度的漂移；第140帧，目标小车进入最后一个弯道，DRACF算法和AutoTrack、ARCF算法依旧跟踪相对成功，STRCF算法发生严重漂移，不能完成准确跟踪。可见，DRACF算法在面对较为复杂的低空目标跟踪时，能够较好地完成跟踪。

图10（c）为UAV20L数据集上的Car16图像序列中的部分关键图像帧的跟踪结果，视频图像包含视角变化、尺度变化等挑战。刚开始时，无人机距离目标较远，目标占视野比率较小，但各种算法均能准确跟踪。随着汽车逐渐靠近无人机，目标占视野比率增大，各种算法只中选择目标的一部分在跟踪框内，也造成了目标特征学习的缺失，因此提供更准确的目标特征对跟踪任务尤为重要。第186～251帧，目标尺度发生严重变化，SRDCF、STRCF和ARCF均发生不同程度漂移；在第260～350帧和第1 114～1 260帧，无人机转动视角发生及目标尺度改变，均影响了跟踪效果，在面对多尺度变化问题时，DRACF算法存在一定缺陷，但与对比算法比较仍能保持稳定跟踪，在长时间目标跟踪任务中表现优异。

4.3.3 消融实验

为了验证DRACF算法的合理性和有效性，实验设计了对比基准算法STRCF在局部响应变化约束模块（Local Response Change Constraint，LRC）、次峰响应变化约束模块（Subpeak Response Change Constraints，SRC）作用下的跟踪对比，表3展示了在UAV123数据集上多种组合的实验结果。可以看出，STRCF算法的成功率和精确度均为最低；而当在STRCF基础上分别引入LRC模块和SRC模块时，成功率和精确度较基准算法均有一定程度提升；DRACF算法的成功率和精确度都排名第一，表明同时使用LRC模块和SRC模块可以有效提高无人机的目标跟踪性能。最后，对比4种算法的跟踪速度，DRACF算法最快。

表3 在UAV123数据集上消融实验结果Tab.3 Ablation experimental results on UAV123 dataset

4.3.4 实时性分析

表4为不同算法在DTB70数据库上的跟踪速度对比，所有算法都在相同的实验平台进行仿真。DRACF算法能够满足跟踪实时性需求，具有实际跟踪场景的应用价值。

表4 各算法的跟踪速度Tab.4 Tracking speed of different algorithms

5 结论

本文在STRCF算法的基础上提出了一种双重响应异常约束的无人机跟踪算法。针对无人机跟踪目标易受视角变化、尺度变化等因素影响的问题，通过计算全局响应峰值旁瓣比和局部响应变化在线动态更新空间正则化参数，实现鲁棒的目标跟踪；加入异常峰值判断机制，计算次峰响应系数，并用该系数实时更新时间正则化参数，对异常进行实时监测，有效抑制异常发生，提升了跟踪器处理各种复杂场景的能力。在UAV123、UAV20L、DTB70数据集上评估本文算法的性能，本文算法相对于STRCF、AutoTrack等主流算法均有了一定幅度的提高，精确度达到71.7%，跟踪平均速度达到48.3帧/s，尤其在UAV20L数据集中的长时间无人机目标跟踪任务中表现优异。但当目标出视野时，本文算法跟踪失败，因此未来将进一步优化跟踪模型以及目标重检测机制，提升算法性能，促进目标跟踪技术的发展及其在无人机中的应用。