基于统计局部特征描述与匹配的点云配准算法

王鑫淼， 李新春， 陶志勇

（辽宁工程技术大学 电子与信息工程学院， 辽宁 葫芦岛 125100）

1 引言

随着LiDAR、Kinect等高精度三维扫描设备的飞速发展，获取自扫描设备的点云［1］数据已经成为三维模型的重要表现形式。然而，受限于扫描仪的自身性能以及扫描场景的复杂条件，所扫描的点云数据存在部分点重叠、缺失和噪声干扰等问题，对其后续应用有很大影响。因此，用于改善扫描点云质量的点云预处理技术［2-3］十分重要。点云配准［4］作为一项重要的点云预处理技术，在点云后续的处理过程中起关键作用。点云配准的目的在于在给定的度量空间下，找到变化矩阵以建立某一点云到另外一个点云的对应关系。点云配准的相关技术已经广泛应用到三维重建、文物修复、地图绘制和自动驾驶等领域。

现有的点云配准算法分为迭代最近点（Iterative Closest Point，ICP）［5］及其变种算法和基于传统几何特征的配准算法。点云配准中应用最广泛的ICP算法是由Besl P J等提出的，该算法通过点云之间的最近点距离建立优化模型以建立配准关系。原始ICP算法在初始姿态［6-8］良好对应时可以得到精确的配准结果，否则容易陷入局部最优解。除此之外，该算法还有鲁棒性差和迭代速度慢等缺点。王宾等提出的应用改进迭代最近点算法［9］在精确配准阶段提出基于双向距离比例的 ICP 算法，提高了配准精度。Zhang J等提出的快速鲁棒ICP算法（Fast and Robust Iterative Closest Point，Fast ICP）［10］利用优化最小化（Majorization-minimization，MM）［11］算法对其进行最小化，在鲁棒性及配准速率上均有提高。ICP及其变种算法是基于点距离建立配准关系，这类方法在初始位姿较差时容易陷入局部最优解，对部分数据缺失点云的配准存在较大缺陷，算法的鲁棒性与全局优化能力仍然存在一定限制。

基于传统几何特征的配准算法通过点对间相同的几何特征建立对应关系进行配准。Salti S等提出的方向直方图描述子［12］（ Signature of Histogram of Orientation，SHOT）在查询点处建立局部坐标系，将邻近点的空间位置信息和几何特征统计信息相结合用作特征描述。Yang J等提出的局部特征统计直方图（Local Feature Statistics Histogram，LFSH）［13］是最近提出的一种基于几何特征的方法，该方法将局部深度、点密度和法线夹角特征进行统计加权，更加全面地描述局部形状几何特征。基于传统几何特征的配准算法鲁棒性更强，但是受几何特征稳定性影响较大，点云特征的求取与对应计算使该类方法配准速率较差。李新春等提出的基于邻域特征点提取和匹配的点云配准算法［14］、刘玉珍等提出的改进的基于快速点特征直方图的ICP点云配准算法［15］和李宇翔等提出的基于改进三维形状上下文的点云配准算法［16］通过提取特征点进行配准。特征点提取能够提高配准速率，但对配准精度有较大影响。

综合来看，可以将ICP及其变种算法与基于传统几何特征的配准算法有机地结合在一起，从而有效提高点云的鲁棒性和配准精度。特征描述符的选取以及对应点匹配是这类方法的研究重点，为进一步配准提供了坚实的基础。

本文提出一种基于统计局部特征描述与匹配的点云配准算法，着重选取高效精确的特征描述符、提高对应点匹配的精度和对ICP算法进行改进。在特征描述阶段，用点云局部密度、点云拟合平面距离方差、高斯曲率和平均曲率构建一个四维的统计局部特征描述符（Statistics of Local Feature Descriptor，SLFD）；在特征匹配阶段，计算点对之间的特征差异，剔除错误点对，提高配准精度；在点云配准阶段，使用平均匹配距离（MMD）对ICP算法进行改进，降低初始位姿对点云配准的影响，进一步提高配准精度。

2 特征描述

特征描述符用来描述点云的局部特征，描述子的选取将直接影响配准质量。为提高配准精度，描述子应充分反映采样点的邻域信息且具有旋转不变性和平移不变性。点云特征描述符有很多表现形式，其中包括法向量、曲率、欧式距离等一维特征，也包含几个一维特征相结合的多维特征。单一的特征不能够完整且准确地描述点云特征。因此，本文选取点云局部密度、点云拟合平面距离方差对点云局部分布进行描述，选取高斯曲率和平均曲率对局部范围弯曲程度进行描述，构建一个四维的统计局部特征描述符（Statistics of Local Feature Descriptor，SLFD）实现对点云局部特征的准确描述。

2.1 特征描述子

2.1.1 点云局部密度

点云是随机分布的不规则数据，不同邻域范围内的局部点云密度不同，因此可以通过局部点云密度对该范围内的点云疏密程度进行描述。点云局部密度通过点云各点的距离平均值进行估算，点之间的距离由点云中某一点与其邻域范围内距离该点最近的点的距离表示。平均距离越小，点云分布越密集；平均距离越大，点云分布越分散。如图1所示，在平坦区域，分布较为分散；在弯曲程度较大的区域，分布较为密集。

图1 点云局部密度示意图Fig.1 Schematic diagram of local density of point cloud

假设查询点pi邻域范围内有k个点，采用KD树方法选取查询点pi的邻近点。与最近欧氏距离法相比，K-D树算法具有更高的效率。用dis(p)表示邻域范围内点p与其他点之间的距离，d(p)表示邻域范围内点p与其他点之间的最小距离，则有：

其邻域范围内k个点到pi的点云局部密度可以表示为：

2.1.2 点云拟合平面距离方差

点云分布不止需要考虑疏密程度，还要考虑点云的不规则分布，然而怎样描述点云的不规则分布是点云特征描述符的一大难点。本文通过邻近点到邻域范围的拟合平面距离的方差对该邻域范围内的点云分布进行有效描述。首先，通过邻域内的点得出邻域范围内点云的拟合平面L；然后，计算邻域内各点与L之间的距离l；最后，通过邻域范围内拟合平面距离l的方差描述该邻域范围内点云分布情况。由图2可以看出，拟合平面距离方差较小时，拟合平面符合点云分布情况，点云分布较为平坦；拟合平面距离方差较大时，拟合平面偏离点云分布情况，点云弯曲程度较大。

图2 拟合平面示意图。（a）弯曲部分；（b）平坦部分。Fig.2 Schematic diagram of the fitting plane. （a）Curved part； （b） Flat part.

图3 SLFD的邻域范围Fig.3 Neighborhood range of SLFD

通过邻域半径中的k个点，利用最小二乘法拟合二次曲面。根据最小二乘原理可得：

将式（3）系数求导并使其为0，解出二次曲面系数。将曲面方程写成曲面L参数方程的形式：

此时，拟合平面距离方差为：

其中：lij为邻近点pij到拟合平面的距离为拟合平面距离的平均值。

2.1.3 高斯曲率和平均曲率

在点云特征描述的过程中，常用的点云特征为法向量和曲率。与法向量相比，曲率具有旋转不变性，并且能够更加直观地对点云邻域范围的弯曲程度进行描述。曲率分为主曲率、高斯曲率和平均曲率。主曲率又分为最大主曲率和最小主曲率，分别表示垂直于最小曲率面和最大曲率面的曲率值。高斯曲率K为两个主曲率的乘积，其数值大小与曲面上的距离有关，与曲面嵌入到空间的方式无关，因此高斯曲率表示点云的内部几何特征。曲面的平均曲率H描述一个曲面嵌入周围空间的曲率，用来表示该曲面的外在弯曲程度。因此，高斯曲率和平均曲率相结合可以全面地描绘出该点的局部弯曲程度。

曲面的第一基本公式可表示为：

曲面的第二基本公式可表示为：

高斯曲率为：

平均曲率为：

2.2 统计局部特征描述符

单一的特征描述符在表达查询点局部特征时具有局限性，在特征匹配的过程中存在误差。多维特征描述符在特征描述时更加准确全面，用点云局部密度、点云拟合平面距离方差、高斯曲率和平均曲率构建一个四维的特征描述符，称为局部特征描述符（Local Feature Descriptor，LFD）。将局部特征中的4个描述子分别定义，点云局部密度为参数f1、局部分布特征为参数f2、高斯曲率为参数f3、平均曲率为参数f4，LFD表示形式为(f1，f2，f3，f4)。

在获取三维点云数据时，由于扫描设备的局限性和噪声因素的影响，所扫描的点云数据存在数据偏差和噪声干扰的问题。异常值和噪声会对平面拟合造成影响，从而导致查询点的邻域特征产生偏差。因此，噪声与异常值的存在是点云特征描述的难点。将查询点与其邻近点的特征描述子进行统计加权［17］可以降低邻域范围内异常值和噪声的影响，查询点与邻近点之间距离的倒数作为权值可削弱距离较远的点对查询点邻域特征的影响。通过统计加权可以得到该查询点的统计局部特征描述符（Statistics of Local Feature Descriptor，SLFD）。

SLFD的计算步骤如下：

步骤1：采用K-D树方法选取查询点pi的邻近点。

步骤2：计算查询点pi的点云局部密度、点云拟合平面距离方差、高斯曲率和平均曲率，得到该点的局部特征描述符LFD。

步骤3：将邻近点pij的LFD与查询点pi的LFD进行统计加权，得到该查询点的SLFD：

3 点云配准

点云配准是通过两点云之间相应的点对建立对应关系，从而建立变换模型的过程。基于传统几何特征的配准算法将两个点云中特征一致的点对相对应，然后建立变换模型，以达到点云配准的目的。本文通过计算点对间的特征差异确定对应关系，并使用平均匹配距离［18］（Mean Match Distance，MMD）替换均方根误差（Root Mean Squared Error，RMSE）作为度量，计算两个点云之间的偏差，该算法称为特征一致ICP算法（Feature Consistency Iterative Closest Point，FC-ICP）。

3.1 特征差异

在点云局部特性描述之后，如何找出相应的匹配点对是点云配准过程中的一个难点。通过两点之间的特征差异（Feature Difference，FD）确定对应关系，两个不同点云间的FD［19］如式（11）所示：

其中：pi为源点云中的点，qi为目标点云中的对应点，fa为第a项参数。

FD越小，两个点之间的特征越相近。当FD为0时，两点之间特征相同。为进一步提高相同特征点对匹配的正确率，选取阈值为0.002。当FD超过阈值时，两个点的特征差别较大。

3.2 FC-ICP算法

配准算法的具体流程图如图4所示。

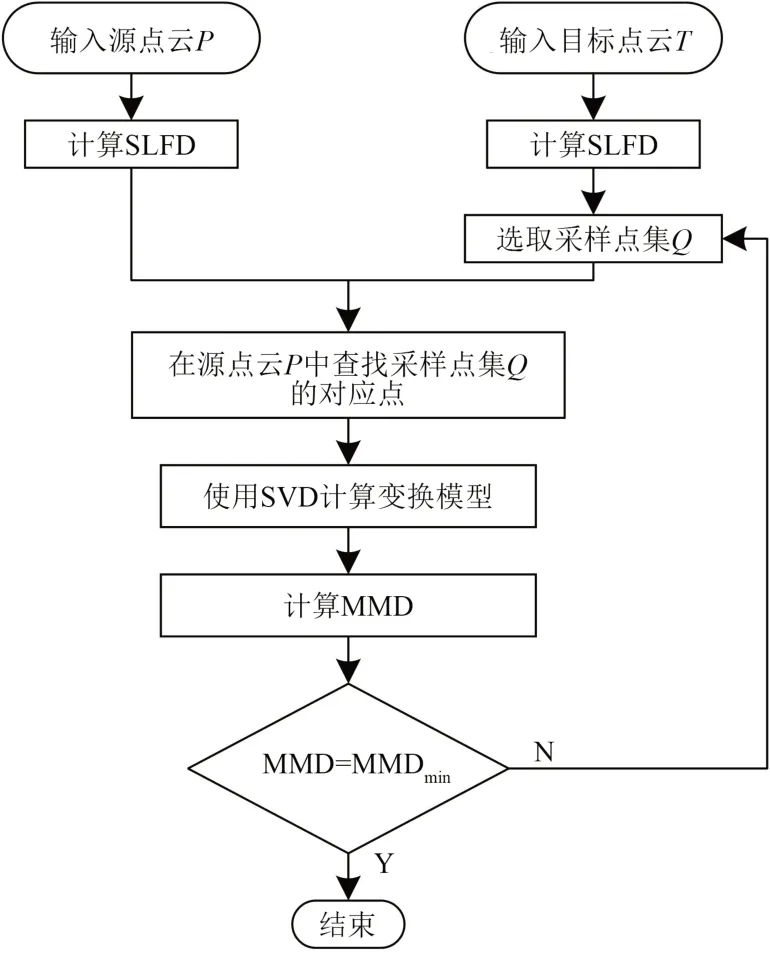
图4 点云配准流程图Fig.4 Flowchart of point cloud registration

点云配准具体实现步骤如下：

步骤1：计算源点云与目标点云的SLFD。

步骤2：使用最远点采样（FPS）［20］的方法从目标点云T中选取m个样本点，将这些点定义为样本点集Q。

步骤3：在源点云P的SLFD中找到与样本点集Q的SLFD相同的点。从点集Q中随机选择一个点作为点云T中样本点的对应，使其FD最小。若FD大于阈值，说明该点不存在对应点，则说明该点邻域内存在噪声和异常值的影响，此时，将点集Q中的该点去除。

步骤4：通过奇异值分解（Singular Value Decomposition，SVD）计算两个点云对应点之间的关系求取源点云到目标点云的变换模型：

其中，b为变换次数。

步骤5：通过计算平均匹配距离MMD度量两个点云之间的匹配程度：

其中：pi为目标点云中的样本点，qi为源点云中SLFH特征与pi相对应的点，u为采样匹配点对数。

步骤6：对上述步骤进行迭代，更新源点云与目标点云之间的变换关系，当MMD达到最小值时，停止迭代。

4 实验与结果

为了验证算法的适用性和可行性，本文在Intel core i5-6200 2.4GHz（CPU） 2G RAM计算机上，通过Visual Studio 2019环境下的C++语言，使用PCL 1.11.0点云公共库进行验证。本文以斯坦福大学点云数据集［21］中的Bunny（35 947个点）、China Dragon（437 645个点）点云模型和Creaform Handy SCAN 700 高精度工业级手持式三维激光扫描仪获得的沐浴露瓶（Bottle）点云［22］（21 469个点）作为实验对象，设置了4组实验。

第一组实验考虑不同初始位姿对点云配准的影响，分别使用初始位姿不同的Bunny模型作为源点云进行配准。第二组实验考虑不同程度数据丢失情况的点云配准，分别选取随机旋转平移变换后点云数据的10%数据缺失情况（32 865个点）、30%数据缺失情况（26 127个点）和50%数据缺失情况（17 325个点）的Bunny模型作为源点云进行配准。第三组实验考虑不同噪声条件的点云配准，使用China Dragon模型，在原始点云旋转后的数据上分别加入标准差为1 mm、2 mm和3 mm的高斯噪声干扰作为源点云进行配准。最后，将实际物品Bottle点云数据进行随机的旋转平移变换、部分数据截取以及加入标准差为2 mm的高斯噪声干扰作为源点云（17 837个点）验证本文算法在实际应用中的效果。

将FC-ICP与ICP算法、基于双向距离比例的 ICP 算法、改进的基于快速点特征直方图的ICP点云配准算法和一种基于改进三维形状上下文的点云配准算法进行对比，验证算法优势。配准时间均由读取点云数据开始，直至配准完成进行计算。将配准后的点云与目标点云之间距离的均方根误差作为点云配准精度评价指标，ξRMSE定义为：

其中，‖R·pi+T-qi‖2表示配准后对应点对之间的欧氏距离。因此均方根误差数值越大，两点云对应点间的距离越大，即点云配准精度越低。

4.1 不同变换状态的点云配准

在三维扫描仪扫描数据的过程中，扫描物品会在不同的环境下产生旋转与位移变化。ICP及其变种算法在初始位姿较差时，容易陷入局部最优解。为分析算法在非理想状况下的配准精度，通过实验对点云进行随机的旋转和平移。将基于双向距离比例的 ICP 算法简写为双向ICP，改进的基于快速点特征直方图的ICP点云配准算法记为Paper1，基于改进三维形状上下文的点云配准记为Paper2。配准情况如图5所示。

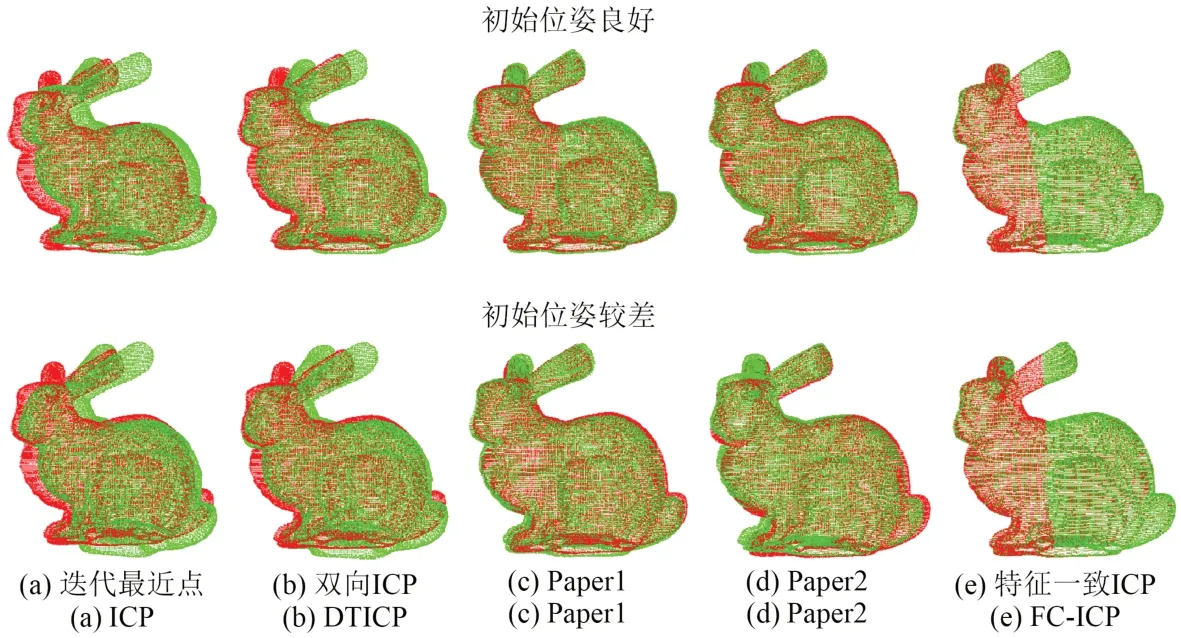
图5 不同变换状态下Bunny模型配准情况Fig.5 Bunny model registration under different transformation states

表1为不同变换状态下Bunny模型的配准数据。由表1可知，ICP和双向ICP算法通过点对间的最小距离进行配准，对初始位姿较差的点云配准精度较差。与两种算法相比，FC-ICP算法精度提高2个量级。与ICP算法相比，FC-ICP算法速率提高25%，与双向ICP算法相比，提升更多。Paper1和Paper2算法通过提取特征点，再通过特征点的局部特征进行对应的方式进行点云配准。特征点提取具有局限性，因此虽然两个算法在初始位姿较差时仍有较好结果，但整体配准精度较差。与Paper1算法相比，FC-ICP算法的配准精度提高93.45%以上，节省24.29%以上的时间。与Paper2算法相比，FC-ICP的配准时间节省24.7%以上，配准精度提高95.29%以上。FC-ICP对整体点云进行特征描述并查找对应点对，由此可见，FC-ICP算法对任意变换状态下的点云均有较好的配准结果。

表1 不同变换状态下Bunny模型配准数据Tab.1 Registration data of Bunny model under different transformation states

4.2 不同程度数据丢失状态的点云配准

在三维扫描仪扫描数据的过程中，遮挡、缺失等环境因素会造成点云数据的不完整。为分析算法在非理想情况下的配准精度，对原始点云数据进行旋转平移变换，再分别选取随机旋转平移变换后点云数据的10%数据缺失情况、30%数据缺失情况和50%数据缺失情况的Bunny模型作为源点云进行配准，对算法进行验证，部分点云配准情况如图6所示。

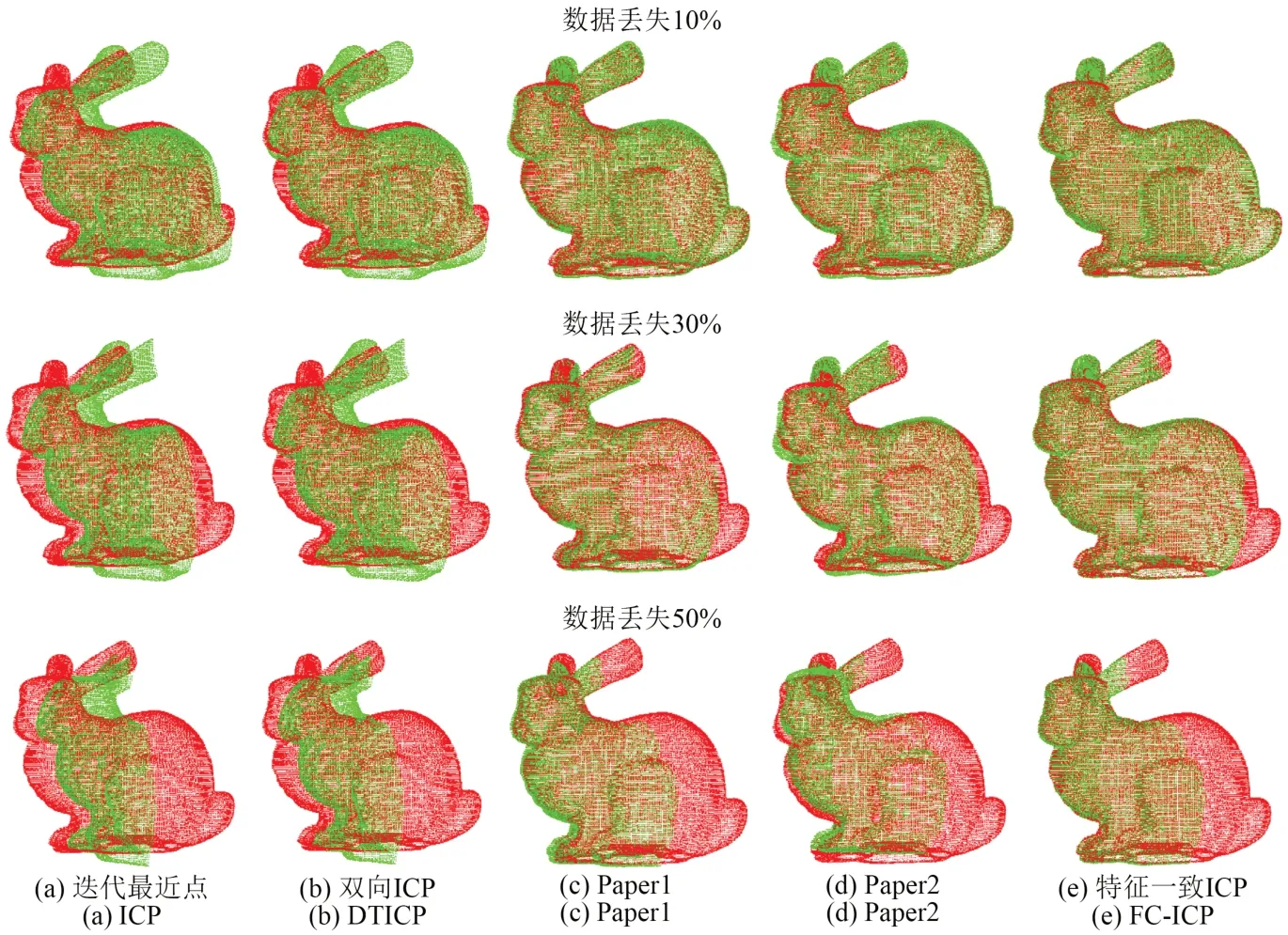
图6 不同程度数据丢失状态下Bunny模型配准情况Fig. 6 Bunny model registration under different degrees of data loss

表2为不同程度数据丢失状态下Bunny模型的配准数据。从表2可以看出，部分数据缺失的点云对于ICP及其变种算法有较大影响，ICP算法和双向ICP算法对于部分点云配准精度较差。FC-ICP配准精度比ICP算法精度提高99.7%以上，节省21.41%以上的时间，比双向ICP算法配准精度提高99.25%，节省更多的时间。部分数据缺失的点云对Paper1和Paper2这类基于传统几何特征的点云配准算法影响较小。与Paper1算法相比，FC-ICP的点云配准精度提高67.33%，速率提高26.1%。与Paper1算法相比，FC-ICP的点云配准精度提高89.11%，速率提高16.3%。FC-ICP算法查找相同的SLFD建立正确的匹配点对，将无法对应的采样点剔除，因此该算法能在点云部分数据缺失的情况下得到更好的配准结果，配准精度有效提高。

表2 不同程度数据丢失状态下Bunny模型配准数据Tab.2 Registration data of Bunny model under different degrees of data loss

4.3 不同程度噪声状态的点云配准

在三维扫描仪扫描数据的过程中，噪声干扰会导致点云数据产生异常。使用China Dragon作为目标点云，对原始点云数据进行随机旋转变换后，分别加入标准差为1 mm、 2 mm和3 mm的随机高斯噪声，对比算法在噪声环境中的配准精度和配准时间，从而验证算法的鲁棒性。从开始读取点云计算时间衡量速率，使用配准前后的均方根误差作为衡量指标。由于China Dragon模型数据量较大，这部分实验时间较长。不同噪声条件下China Dragon模型配准情况如图7所示。

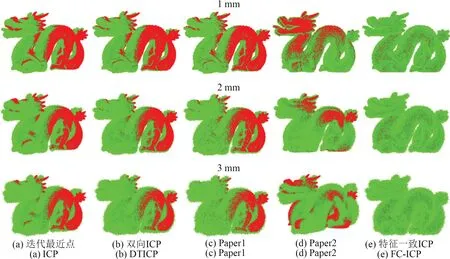
图7 不同噪声条件下China Dragon模型配准情况Fig.7 China Dragon model registration under different noise conditions

表3为不同噪声条件下China Dragon模型配准数据。根据表3可知，FC-ICP在较大噪声情况下，SLFD受噪声影响，点对匹配不准确，点云模型变换迭代次数增多，配准时间增加。ICP算法与双向ICP算法陷入最优解，配准精度较小。由于Paper1和Paper2算法都是通过点云局部特征进行特征点提取，噪声对特征点提取存在较大影响。与Paper1算法相比，FC-ICP的配准精度提高48.95%，速率提高5.24%。Paper2算法受噪声影响较大，鲁棒性较差，FC-ICP的配准精度提高22.75%，配准时间节省6.89%。由此可见，FC-ICP算法在噪声较小时，能够有效完成配准；在噪声较大时，估算点云曲率需对邻域范围进行平面拟合，拟合平面存在偏差，估算曲率误差较大，FC-ICP鲁棒性仍需提高。

4.4 实际物品的点云配准

为了验证FC-ICP在实际应用中的效果，以Creaform Handy SCAN 700 高精度工业级手持式三维激光扫描仪获得的沐浴露瓶（Bottle）点云作为实验数据。为了模拟点云在实际情况下的配准过程，对原始数据进行随机的旋转平移变换，切割部分数据，并且加入均方差为2 mm的高斯噪声。图8为Bottle实物的配准情况，表4为配准误差和配准时间。

表4 Bottle实物的配准数据Tab.4 Registration data of Bottle

图8 实际物品Bottle配准情况Fig.8 Actual registration of Bottle model

结合表4可以看出，在实物配准过程中，ICP算法和双向ICP算法陷入局部最优解。Paper1和Paper2算法受噪声影响，精度较低。与其他算法相比，FC-ICP算法精确度提高70.52%以上，配准速率提高9.92%以上。

5 结论

针对点云配准在初始位姿差、数据缺失和噪声干扰情况下的问题，本文提出一种基于统计局部特征描述与匹配的点云配准算法。通过点云局部密度、点云拟合平面距离方差、高斯曲率和平均曲率构建了一个四维的统计局部特征描述符（Statistics of Local Feature Descriptor，SLFD），更加准确全面地描述点云局部特征。通过点对间的特征差异查找对应点，确定对应关系，使用改进的FC-ICP算法对点云模型进行配准。由斯坦福大学点云数据集和实物数据集的点云配准实验结果可以看出，不存在噪声时，配准精度提高67.33%以上；存在噪声时，配准精度提高22.75%以上。当点云数据较少时，配准速率提高较大，节省16.3%的时间；当点云数据较多时，速率提升5.24%。由此可见，在不同的环境下，本文算法与ICP算法、双向ICP算法、改进的基于快速点特征直方图的ICP点云配准算法和基于改进三维形状上下文的点云配准相比较，具有较高的配准精度和配准速率，鲁棒性更强。由于本文算法需要计算大量局部特征，因此该算法配准速率较慢，时效性差，对大场景点云配准适用性较差。后续需要加快配准速率，使其时效性增强，增加大场景点云配准的适用性。