浅析EEAC法在电网安全稳定控制分析中的应用

芦 飞

（南京南瑞继保工程技术有限公司）

0 引言

提高电网的稳定性可以通过加强网络结构的方式来实现，但是在某些情形下，这样增加巨额的投入并不切合实际；还有一个非常有用且投入不大的方法，是通过安全稳定控制措施来改善系统的稳定性，通过对几种不同类型的稳定性控制方法进行研究，得出了一些有益的结论［1-2］。

1 安全稳定控制系统的决策方式

在地区电力系统安全稳定的应急管理中，所有应急管理工作均需依据决策表进行。如果在当前的决策表格中，假定X代表该制度如何运作，Y代表事件集合，Z代表事件的控制措施，则按照决策表的不同情况，可以将决策划分为以下三类。

1.1 离线决策

该方法在国际和国内上都有普遍的应用。X、Y是无法确定的，为了建立一个判断表格，必须对操作模式及发生的情况进行预测。该方法离线计算量大，自适应差，而且需要较高的专业技术和操作经验，存在不匹配或控制精度低等情况［3］。

1.2 在线预决策

若按照目前的运作模式，即当X确定，只能预见某些事件，迅速作出决定。该方法的假设条件为在几分钟之内不会有较大的改变，从而可以解决条件不匹配的问题。日本CEPCO公司开发的晶闸管投切电容器（Thyristor Switched Capacitor，TSC）稳定控制系统和南京自动控制研究所开发的OPS-1型在线预测控制系统是该领域比较成熟的。该方法涉及到三个关键技术：基于故障扫描的小缺陷筛查、基于精细建模的大缺陷检测和基于并行算法的高效求解［4］。该方法是目前地区电网稳定控制技术的发展方向，也是一个热门课题。

1.3 实时决策

实时决策是最为理想的一种决策方式，也是安全稳定控制的发展方向，它彻底解决了操作条件与失效不匹配的问题。但这意味着它的技术较为复杂，这种决策防控手段只能在短期内发挥作用。需要利用相量测量单元（Phasor Measurement Unit，PMU）来对整个电力系统进行实时的监测，用高速通讯技术传送资料，良好的计算方法可以迅速、准确地对被干扰的体系进行预报和判定。三种控制策略的具体比较见下表。

表 三种控制策略对比表

2 EEAC原理

EEAC方法在多机系统中推广了等面积规则。它的本质是在一定条件下，对于给定的故障，将机组划分为两个互为补充的组，每一个组由单个等值机替代，并将其进一步等值成单机无穷大 （OMIB）系统［5］。利用等面积法则对系统的暂态稳定性进行计算。EEAC方法是目前仅有的一种被严格论证的方法。它的工作原理如图1所示。

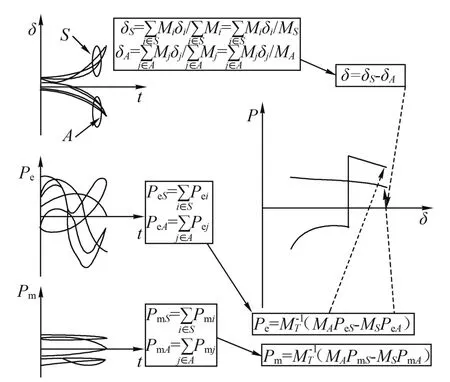
图1 EEAC法示意图

一个带有n个发电机的系统，对于第i个发电机，其动态方程为：

其中，Tji是第i个发电机的惯性时间常数；Pmi是电磁功率；Pei是机械功率。

令Mi＝Tjiωi，则方程（1）可改写为：

在系统不稳定的条件下，该系统共有I＝2n－2种不同的方式，将n台发电机划分成两个非空的互补组，即集合S和A，S、A同时满足以下关系：

对于某个特定的划分，将属于同一群的机组的动态方程相加，结果如下：

上述公式还包括所有n个角的变量，观测起来很不方便，在此将其转化成一个平面的方程组，以便观测。从n机系统到两机系统的映射过程如下：

由此，可把式（4）改写成二元微分方程：

要把EEAC应用于上述的两机体系，需要把这两机体系再映射为OMIB体系。令：

由公式（5）、（6）、（7）可得：

以上过程完成了多机系统到单机无穷大系统的映射，其部分惯性中心可表示为CPOI（n，l）。这种变换保留了多机系统的稳定特性，因而能够用来判断多机系统的稳定性，其证明如下：如果存在两个或更多的不稳定群，则每一个不稳定群的功率角包络间的间隔将趋向无穷大，这种间隔称为无边界功角（UAG）。要观察到UAG，就需要较长的积分时间，实际应用中，通常采用有界门槛值作为是否存在UAG的判断标准，当有功角度的余隙超过临界点，则视为不稳定。在一定的观测时间内，将n台机组按照功角从大到小的顺序来排列，从而产生n－1个不同的功角间隙。每个间隔将整个体系分成两种不同的补充类群，其中最前面的一类称为关键类，即集合S，其余的机组为剩余类，即集合A，因此有n-1种不同的划分方法。对于任何一种划分方式，通过公式（5）计算所得的δS必然大于S群功角的下包络线，δA必然小于A群功角的上包络线，因此δS－δA必然大于该方式下的功角间隙。两互补集合内发电机输出的电功率为：

在EEAC法中，发电机采用经典模型，即发电机直轴瞬态阻抗电势保持不变，因此有Ei（t）＝Ei，Ej（t）＝Ej，利用式（7），并令：

公式（9）可转化成如下公式：

EEAC法中所考虑的两群模式是理想的两群模式，群内各发电机同调，即互补集合内各发电机功角间隙在整个动态过程中保持恒定，所以各受扰轨迹相对于部分惯量中心的偏移角均为常数，由初始工况的潮流计算可得到：

把公式（12）代入到公式（11），可得：

按照从多机系统到两机系统的聚合公式，可得到两机系统的电磁功率表达式，如下：

再利用两机系统映射到OMIB系统的变换公式，可得：

其中，Pc、Pmax、v为等值OMIB系统的结构参数。

如果在动态过程中没有切除发电机，则映射到OMIB系统的机械输入功率为：

把式（16）、（18）代入到式（8）中，即为EEAC法映射到单机无穷大（OMIB）系统的动态方程。由于故障前后的网络结构不同，因此Pe也就不同。经过部分惯性中心CPOI（n，l）映射后，OMIB系统示意图如图2所示。

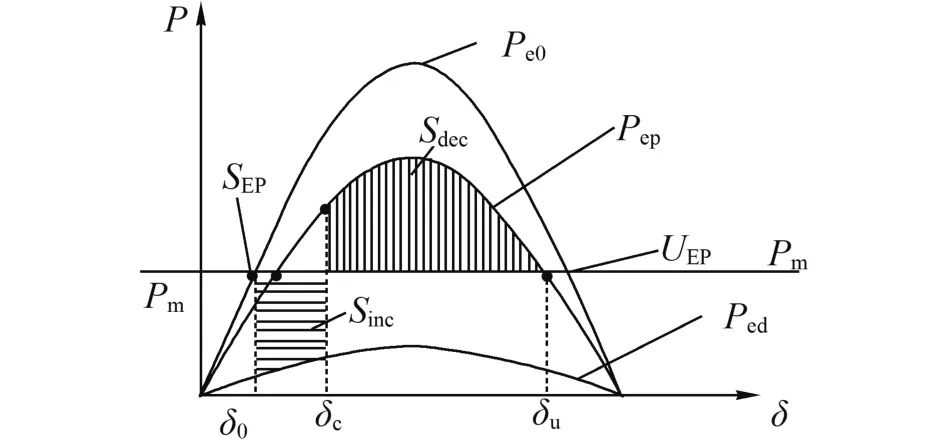
图2 映射后OMIB系统示意图

EEAC的核心是保留原有集成空间的整体结构，只将观测空间解耦为单个机械无穷大系统，同时保留原有机械动力学的稳定性，因此这一变换可用于判断系统的稳定性［6］。

3 EEAC法的优势

（1）计算速度快且精度高，能够提供稳定裕度

目前，国内大多基于电压、频率、n－1功率极限等对电网安全稳定性进行评估的方法虽然较为详细，但耗时较多，其中的各种因素对评估结果的影响较大。EEAC方法最大的优点是可以迅速对故障时的稳定余量和临界切除时间（CCT）进行准确求解，使调度人员可以更好地了解电网的状态，具有更强的针对性。

（2）可主导模式概念的应用

基于EEAC的控制方法，能够辨识各种瞬态功率不稳定模态，将各机组分成不同调的组别。这有助于正确建立电力系统主要网络架构，同时对PMU的布置进行最优化处理，实现了用最小的PMU来描述受多种干扰时的基本动力学特性。

（3）能够全面快速地设置扰动形式

对电力系统的实时稳定性进行了研究与探讨，EEAC法刚好可以迅速地给出全网各点跳闸的故障表，批量地解决了所有问题，求出了整个网络的稳定性余量和CCT值，这样可以迅速地对整个网络进行分析和评估，并形成对应的策略表。利用EEAC方法可以对多摆的稳定状态进行判断，运算耗时短，但在此过程中，还是使用了一个有效的数值来作为状态变量，并且评价的准确性取决于对同调群的辨识准确性。

4 结束语

本文首先阐述了安全稳定控制系统的基本模式和决策方法，在此基础上，对电网的安全性和稳定性进行了深入的研究；其次，深入研究了基于广域测量系统的安全性与稳定性的工作机制，并给出了基于扩展等面积算法的映射实现方案；最后，对广域测量系统与EEAC法在安全与稳定性监控中的优越性及未来发展趋势进行了论述。