基于行波的电力电缆故障测距主要问题研究

陆世进 魏 星 刘 磊

（南通轨道交通集团有限公司运营分公司）

0 引言

随着我国城市化程度越来越高，城市土地可用面积越来越低，传统的架空输电线路无法满足城市化生产、生活所需［1-2］。而交联聚乙烯电缆具有占地面积小、耐腐蚀、负载大等优点，逐渐取代了传统的架空输电线路，成为了城市输送电能的主要方式。交联聚乙烯电缆深埋于地下，当受到雨水、生产工艺、外力破坏等情况时，极易发生绝缘损伤的情况。一般情况下，电缆故障都是渐发性故障，起始阶段会伴随微弱的放电，直到主绝缘彻底击穿才会发生故障跳闸［3］，适用于架空线路的故障测距手段针对于电缆的渐发性故障不一定适用，因此，本文选用在架空输电线路上成熟应用的行波法故障测距进行交联聚乙烯电缆的故障测距。对于影响输电电缆行波法故障测距的因素作出以下总结：（1）在进行行波法故障测距时，对于常见的输电电缆结构（单T接电缆、多T接电缆、电缆转架空）进行了行波传输折反射研究［4-5］；（2）电缆线路波阻抗较大，同时线路杂散电容较大，受到行波的色散效应影响较高，对于电缆采用行波法故障测距进行行波的波速计算时，不同于架空输电线路，不能采用单一固定波速进行电缆的波速确定； （3）由于行波在电缆中传输的关系导致了行波到达监测终端的波头时刻问题，行波波头到达监测终端的时刻直接影响了故障定位精度［6］。

在行波色散方面，昆明理工大学束洪春及哈尔滨工业大学董俊等人提出了一种利用故障频带和TT变换的电缆单端行波故障测距方法，该方法从一定程度上解决了行波在电缆中传输的波速问题，采用了单端行波法进行电缆的故障精确定位，如果利用单端行波法进行故障定位，在监测终端无法监测到故障点的反射波时，一般情况下难以实现故障精确定位［7］。

在电缆故障测距波头时刻检测方面，安徽理工大学韩雅琦提出了一种基于EEMD与小波变换的电缆故障定位方法，利用经验模态分解与小波变换结合的形式提取出了特征电缆故障模态时刻，从而实现了电缆的故障时刻判定，该方法需要通过大量的计算以及反推验证的方法进行电缆故障行波波头的标定，同时小波变换的小波函数及尺度函数都会对行波法故障测距波头时刻产生影响［8］。

本文主要从上述几个方面进行电力电缆行波故障测距研究，对相应的问题提出了一定的见解，为未来行波法电力电缆故障测距提供了理论支撑和研究方向的参考。

1 行波法故障定位基本原理

行波法故障定位于上个世纪被提出，但是受到了当时传感器采集精度、行波波头时刻难以标记的影响，行波法故障测距并没有在输电线路中得到应用。直到20世纪末期，随着高精度的数字化传感器以及小波变换等一系列数字信号处理方法的出现，行波法故障测距得以在输电线路中应用。行波法故障测距基本分为如下几类：A型行波法故障测距（单端行波法故障测距）；B型行波法故障测距 （双端行波法测距）；C型行波法故障测距 （注入式行波法故障测距）；D型行波法故障测距（依赖于GPS的双端行波法测距）［9］。上述经典的行波法故障测距基本可以分为两类，一类为单端行波法故障测距，另一类为双端行波法故障测距。由于单端行波法故障测距受到系统运行方式以及故障点过渡阻抗的影响，因此双端行波法故障测距被广泛应用于输电线路故障测距中，双端行波法故障测距基本原理如图1所示。

图1 双端行波法故障测距基本原理

图1 中，A、B为两变电站；m、n为两行波监测终端；G为输电线路接地点；Xm、Xn分别为故障点和监测终端m、n之间的距离；t1、t2为行波分别到达监测终端m、n的行波波头时刻。

通过行波故障测距基本原理公式（1）～（3）可知，在输电线路中影响行波法故障测距的主要因素为行波在输电线路中传输的波速、以及行波到达监测终端的波头时刻，而双端的对时问题结合现行的北斗GPS系统基本不会对行波法故障测距产生影响。因此分别对影响行波法故障定位精度的因素进行探讨。

式中，L为待监测终端之间的电缆距离；v为行波在电缆线路中传输的波速度。

2 行波在电缆中传输的折反射效应

对于输电线路中单导线对地的等值电路，通过微分的方法可以将单根导线近似成无限个长度为dx的导线组成。假设单位长度的导线dx的电感、电阻、对地电容、对地电导分别为L0、R0、C0、g0，则每个单位长度的导线对应的参数分别为L0dx、R0dx、C0dx、R0dx。以dx长度的导线为例［10］，当单位长度的导线发生故障时，可等效成如图2所示的电路图。

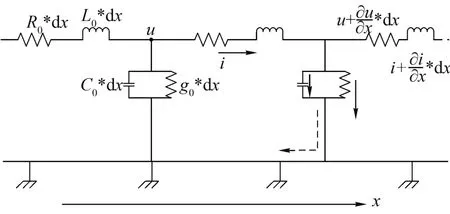
图2 单位长度等效电路图

如图2所示的系统回路中，根据基尔霍夫电流、电压定律可知：

式中，u为图2中测量点电压；i为回路中电流；R0为导线电阻；C0为导体对地导纳；g0为导线对地电导。对上式进行去除二阶无穷小，同时采用拉氏变换可得：

即导线单位长度的波阻抗只与导线单位长度的电感量L0、导线单位长度的电容量C0有关，与其他参量无关，而行波在遇到波阻抗不联系的点会发生折反射，分别讨论行波在通过不同结构的电缆时行波折反射情况。

2.1 电缆T接架空线路

行波在电缆中传输遇到波阻抗不连续的点会发生折反射，现阶段常见的电力电缆线路如图3所示。

图3 电缆T接架空线路结构示意图

如图3所示，该结构为电缆架空混架的情况，从电缆中T接架空线路出来，通过查阅相关文献，电缆线路的波阻抗约为架空线路波阻抗的0.1倍，以图3为例，入射行波电流为I0，设电缆的波阻抗为Z0，则架空线路的波阻抗为10Z0，根据行波的折反射规律，经过架空线路反射之后的行波电流I1为：

经过架空线路折射之后的行波电流I2为：

经过电缆线路折射之后的行波电流I3为：

2.2 电缆T接电缆线路

行波在电缆中传输遇到波阻抗不连续的点会发生折反射，在实际输电电缆系统中常会遇到电缆线路T接电缆线路的情况，如图4所示。

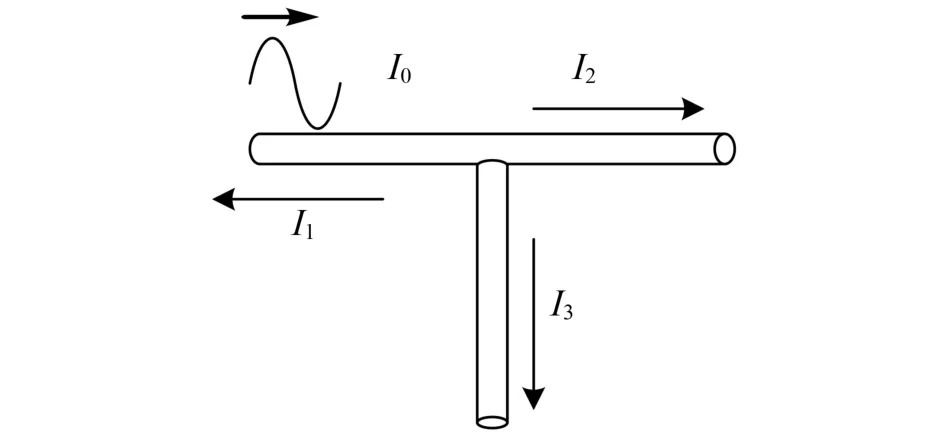
图4 电缆T接电缆线路结构示意图

如图4所示，电缆T接电缆线路为输电电缆线路中较为常见的形式结构，采用同类电缆进行T接，假设主线电缆与T接电缆的材质一致，则主线电缆的波阻抗和支线电缆的波阻抗一致，假设电缆的波阻抗均为Z，依据行波在电缆中传输的折反射规律，经过电缆线路反射之后的行波电流I1为：

经过架空线路折射之后的行波电流I2为：

经过电缆线路折射之后的行波电流I3为：

对上述几种常见的输电电缆T接情况进行了总结归纳，提取了行波传输的折反射规律，利用此规律，在进行输电电缆行波故障测距时，可合理的安装电缆行波故障监测装置，从而实现行波的全方位监测。

3 行波在电缆中传输的波速度

行波是指行走的电磁波，应用于输电电缆线路中，行波基本上以电场能和磁场能相互变换的过程在输电电缆芯线中传播，一般在实际工程应用中，会通过忽略其对地导纳进行行波的波速度计算，行波在输电电缆芯线中传播的波动方程为：

式中，∂u为输电电缆发生故障时故障点电压偏微分值；∂i为输电电缆发生故障时故障点电流偏微分值；∂x2为输电电缆发生故障时故障点距离平方的偏微分值；∂t2为输电电缆发生故障时行波传输时间平方的偏微分值；L为电缆线路故障时线路电感矩阵；C为电缆线路发生故障时电容矩阵。

当电缆线路固定时，一般情况下其相应的参数也是固定的，同时其L、C矩阵参数也是固定的。因此，可以通过式（13）得出行波在线路中传输的波过程只与传输的时间和距离有关，与线路本身参数基本无关。则针对电缆线路进行Clark变换和矩阵解耦，通过解耦之后可得：

式中，L0、C0为解耦后对应的模量单位长度的电感、电容参数。一般情况下，电缆线路铺设完成时，其参数也能够直接确认，则可基本确认电缆线路的行波传播波速。

在电力电缆故障测距实际应用中，行波在电缆中传输波速难以通过上述方法进行精确计算，电缆主体成分不同于架空输电线路，其成分复杂。同时，当电缆线路发生故障跳闸时，故障时刻行波包含了多种频率成分。其中，频率越高的成分传播的速度也越快，其传播的衰减速度也越快，相反，频率越低的成分行波的传播速度越慢，其衰减也越慢。受到了行波色散特性的影响，行波在输电电缆中传输时，行波的波头和相位角都会发生畸变，因此采用架空输电线路固定经验波速法进行行波故障精确定位必然会导致故障点定位出现偏差，如图5所示为电缆故障中行波传输距离的衰减特性。

图5 电缆故障中行波传输随距离的衰减特性

通过收集输电电缆中行波传输的数据集合，仿真电缆故障情况进行速度的标记，结合大量现场数据与仿真情况，进行不同频率的故障行波的传播速度标定，依据中心频谱法对输电电缆行波进行了波速曲线的标定，如图6所示为中心频谱法测定电缆脉宽与波速之间的关系图。

图6 仿真行波脉宽与波速之间的关系图

由图6可知，随着电力电缆中故障行波脉宽的变大，故障时刻行波在电力电缆中传输的波速也逐渐变慢，趋于稳定。行波传感器采用还原度较高的罗氏线圈传感器进行采集，当电缆线路发生故障跳闸时，利用行波脉宽值所对应的波速值进行故障点精确定位，即可缩小由行波传播的波速带来的故障定位误差。

同时，当行波监测装置安装在输电电缆现场时，利用合闸及串入行波结合故障监测装置的距离进行区段电缆的波速校核同样可实现行波波速的核定。进而减小因行波在电缆传播波速原因导致的故障精确定位带来的误差。

4 行波在电缆中传输的波头时刻

由于行波传播的色散原因，故障时刻行波随着传输距离的变化，如图5所示，行波的峰值点与起始点都会发生变化，这导致在确定波头时刻时会出现波头时刻确认出现偏差的情况。此时如果采用传统的小波变换或者希尔伯特-黄变换进行行波的波头故障时刻求解，必然会出现故障测距存在偏差的情况，尤其是系统在高阻接地的情况下，受到系统运行情况的影响较大，根据输电电缆历史故障情况，当故障过渡电阻高于1000Ω时，行波监测装置通常难以识别故障时刻行波波头时刻，进而导致了行波法故障精确定位的失败。由于输电线路电缆故障点产生的行波向两边传播，且向两边传播的行波具有很大程度的相似性，而一般情况下在进行输电电缆行波故障测距时采用双端行波法故障测距，因此针对此种电缆故障测距情况可采用相位平移法进行输电电缆行波故障测距波头识别，具体步骤如下：

（1）对故障时刻行波进行处理，基于故障点产生的行波的相似度较高，利用峰值较大的行波进行峰值对齐；

（2）将双端故障时刻行波放入同一个时间轴坐标中，将对齐峰值的行波电流进行平移，平移对齐第一个行波波峰；

（3）如果出现第一个波峰两监测装置不同的情况，需要将其中一个行波电流波形进行翻转，从而实现对齐；

（4）一般情况下，输电电缆线路故障时其主波波头都难以定量计算，相位平移的方法，主要对齐故障行波上升沿趋势，即波峰前，即可实现行波波头时间差的计算，将其带入式（1） ～（3）中即可实现行波故障点精确定位。

5 结束语

本文从输电电缆行波法故障测距角度出发，对现阶段输电电缆行波法故障测距主要面临的问题进行了总结，同时给出了相应的解决方案。无论是折反射方面，还是行波在电缆中传输的波速以及行波传输的波头时刻都是电缆行波法故障测距所不可避免的问题，针对上述问题提出了相应的解决方案，同时也给行波法输电电缆故障测距提供了相应的研究方向及思路。