基于电压波动下的温控负荷特性及其控制策略

陈 琦 李培强 刁涵彬

（1.福建理工大学 2.湖南大学）

0 引言

随着人民生活水平的提高，大电网负荷侧以空调负荷（air conditioning load，ACL）为主的综合温控负荷所占比例不断增高。据国际能源署预计，2050年全球空调总能耗将等于中国当前各行业的电力需求量之和［1］。全球各种停电事故分析指出负荷特性导致的电网电压稳定性恶化是各项停电事故高发不下最为关键、直接的因素。而在实际应用中，空调负荷密集区域的高压节点一般为高压配电所和变电所，属于重负荷节点，连接着大量的民用、商业和工业用电，一旦发生电压崩溃而停电，将会对日常生活生产工作造成重大影响和经济损失［2］。

目前，国内外学者针对温控空调类负荷的电压稳定特性已开展了一些研究。文献［3］针对空调负荷停机特性、启动特性以及电压扰动特性建立了空调负荷的四种重要运行状态的负荷模型；文献［4］根据统计数据分析得出结论：在空调负荷运行密集的地区更容易发生电网电压延迟恢复现象。但上述研究都未对比不同类型的空调负荷的负荷特性对电网电压稳定性的影响。

本文通过提出改善空调负荷特性的自主控制策略、延迟参考转速恢复时间的控制策略，以提升电网电压稳定性的控制方法。首先，基于温控负荷数学特性，建立定频空调和变频空调电机负荷模型，提出一种基于电网电压陡降情形下转速的自主调速控制策略，同时增设转速恢复缓冲时间以改善温控负荷对电网节点无功功率的冲击，最后，基于Matlab／Simulink对定频空调、传统变频空调以及采用自主控制策略的变频空调进行仿真分析，结果表明该方法是一种有效的、实用的、控制精度较高的温控负荷控制方法。

1 温控空调负荷模型

由于压缩机功率占空调运行总功率的90%以上［5］，因此本文基于压缩机驱动电机的形式研究温控负荷的静态特性和电压动态特性［6］，以市场上常见的空调负荷为例，分别对定频空调和变频空调数学模型进行具体分析。

1.1 定频空调模型

定频空调核心部件压缩机的驱动电机采用三相异步电机，可以得到与定子磁场同步旋转坐标系下的三阶感应电动机方程。

状态方程为：

式中，E′d、E′q分别为感应电动机d、q轴暂态电势；X＝Xr＋Xm为转子开路时的开路电抗；X′＝Xs＋XrXm／（Xr＋Xm）为转子堵转的短路电抗；Id、Iq为d、q轴电流；ωb为定子磁场转速；ωt为转子转速；T0′＝（Xr＋Xm）／（ω0Rr）为暂态开路时间常数；ω为感应电机同步角速度；Te、Tm分别为电磁转矩和机械转矩。

单台空调的输出功率方程为：

式中，Tm为机械转矩；ωm为永磁同步电机同步角速度。

1.2 变频空调模型

由于定频空调只能通过启停控制来实现平均制冷效果，而循环往复的间断工作给空调的温度控制精度带来了很大的局限性，因此目前市场空调占有率主要以变频空调为主，可用电压方程、磁链方程、转矩方程和运动方程四部分来描述变频空调数学模型。

（1）基于坐标系的定子电压方程，基于ABC坐标系的定子电压方程，如式（6）所示：

功率方程为：

式中，m为空调台数；UA、UB、UC为三相定子电压暂态值；iA、iB、iC为三相定子电流暂态值；ψA、ψB、ψC为三相定子磁链暂态值；RA、RB、RC为三相定子电阻暂态值。

将其转化为基于d-q坐标系下转子电压方程，表示为：

（2）关于d-q轴上的磁链方程为：

将式（7）转化为d-q坐标系功率方程：

（3）基于d-q坐标系的转矩方程为：

式中，Te为电磁转矩；P为极对数；ψs为转子磁链；文中采用表凸式转子，Ld＝Lq，因此式（11）化简为：

（4）基于d-q坐标系的机械方程为：

其中，ωr为机械角速度；Te为电磁转矩；TL为负载转矩；J为转动惯量；B为转动摩擦系数，转动摩擦系数较小，在电机实际运行系统中，摩擦损失一般只占电机机械总损耗的1%左右［7］。

2 电压陡降时空调的自主控制策略

已知恒功率负荷是加剧电网电压稳定性进一步恶化的重要因素，而恒阻抗负荷是一种电压敏感型负荷，当电网电压下降时，为了保持阻抗不变，通过负荷的电流也会下降，因此恒阻抗负荷比例的增加也会改善前述不利影响并维持电压稳定性［8］。本文通过合理的控制策略使空调由恒功率特性转变为恒阻抗特性，目的在于改善温控负荷的负荷特性以缓解对电网的冲击。

从机械系统来看：

式中，Ω＝2πn／60为对应于转速n的角速度。

而此时从电气角度来看，考虑将变频空调负荷通过合理的控制策略使其在电压扰动下由恒功率负荷转化为恒阻抗负荷。若在恒阻抗负荷条件下，电网负荷侧的功率应与电压平方成比例关系，而电磁功率PM是电功率转化为机械功率的部分，其中效率η近似为常数，由此建立起了网侧输入功率与机侧输出功率的关系：

式中，U为电网侧输入电压；R为电网侧电阻。

此外,很多学者在多通道人机交互中提出用视线追踪代替鼠标光标移动,用眨眼等视觉行为代替鼠标点击操作,此类概念部分已应用于VR交互设备[16].这些新型交互技术的核心基础是对用户操作行为意图与眼动特征关系的准确把握,因此,基于眼动特征的用户意图感知和行为预测具有重要的研究意义.

联立式（14）、式（15），可得：

整理可得空调负荷解析表达式为：

式中，A＝90η／（πTLR）。

试验表明，当变频空调的功率高于额定功率的20%时，其效率几乎保持恒定［9］，同时压缩机负载TL近似于恒转矩负载，因此对于同一类空调，A为常数。

依据公式（17），可得电压-转速控制策略如图1所示，由于在电力系统正常运行期间，电压出现小幅度波动是正常现象，因此当电压波动范围在±10%内，该自主控制策略不动作，当额定电压为220V，额定转速为1500r／min时，可得出转子速度控制策略如下：

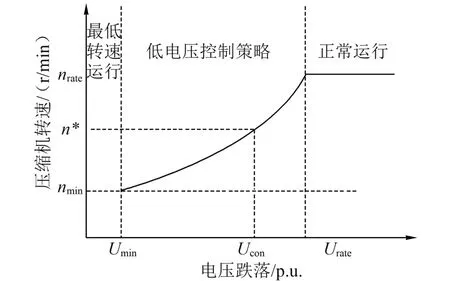
图1 电压-转速理想控制图

当电压差值小于0.1urate时，系统电压处于正常波动范围，空调压缩机维持额定转速；当电压差值大于0.4urate小于0.9urate时，转速根据电压调整；当电压差值小于0.4urate时，转子转速维持在最低值。同时设置输出负载转矩为恒定值，以模拟温控负荷驱动电机的恒转矩特性，对于转速调节采用PI控制，将给定初始转速n0和反馈转速n作差得到误差δ，将差值输入到速度调节器后输出转矩电流i*q，将其与经过坐标变换的电机实际电流iq作差，其值经过电流调节器后，得到d-q坐标系下的q轴电压值，同理采取id＝0的控制方式，得出d轴电压值，通过实时控制励磁电压，进而改变压缩机转速，如图2所示。

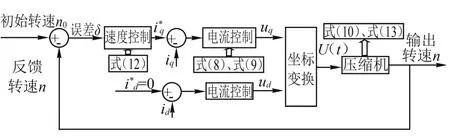
图2 转速PI理想控制图

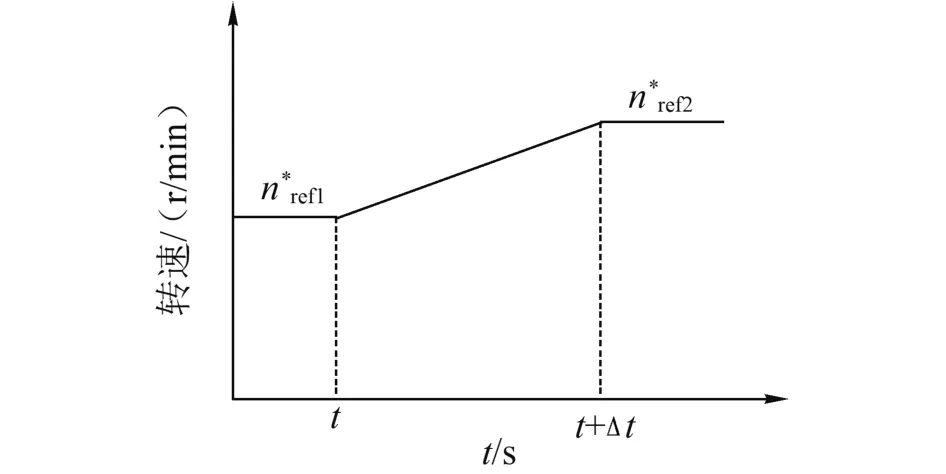
图3 参考转速延迟恢复时间

3 算例分析

3.1 系统参数

采用MATLAB／Simulink环境下搭建的空调数学模型分为电源模块、整流逆变模块、坐标变换模块、自主控制策略模块、SVPWM模块以及PI调节模块。

单台定频空调的压缩机驱动电机采用额定值为220V、50Hz、2kW的三相异步电机，具体参数见表1。

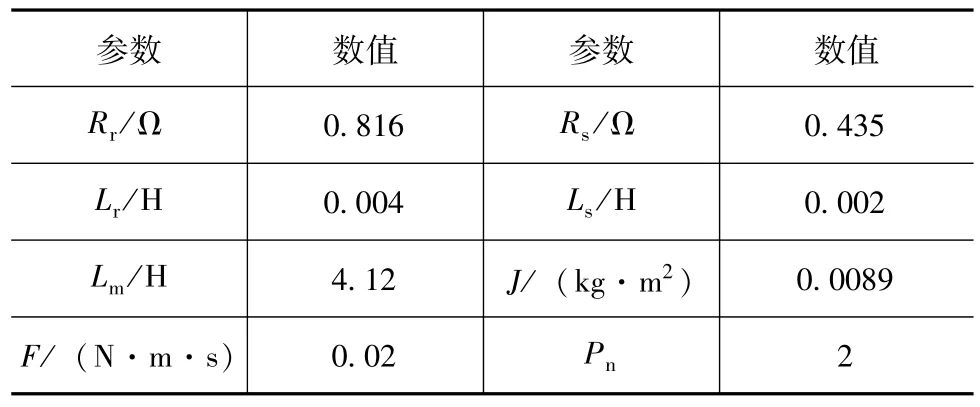
表1 三相异步电机参数

单台变频空调压缩机驱动电机采用额定值为220V、50Hz、2kW 的永磁同步电机，负荷模型参数设置见表2。

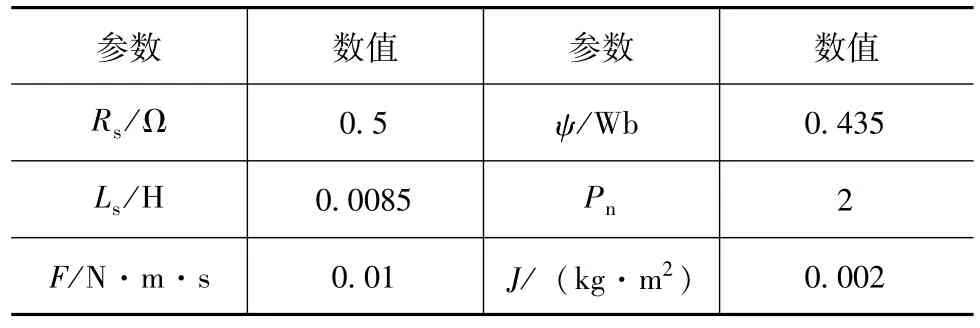
表2 永磁同步电机参数

综合考虑验证控制策略的合理性，本文针对电压幅值和电压跌落时间两个关键参数，电压跌落至原幅值的70%并持续0.5s。本文选取速度外环：d轴电流调节器参数Kp＝13.5，Ki＝125；q轴电流调节器参数Kp＝0.3，Ki＝125。

3.2 算例结果分析

当电压跌落到原电压的70%时（如图4所示），传统定频空调电流瞬时值增至额定电流的1.5倍，当电压恢复瞬间，定频电流瞬时值增大到额定电流的2.4倍，这种电流过大的响应特性容易对电网设备造成冲击。

图4 电压跌落至额定电压的70%并持续0.5s的交流母线电压

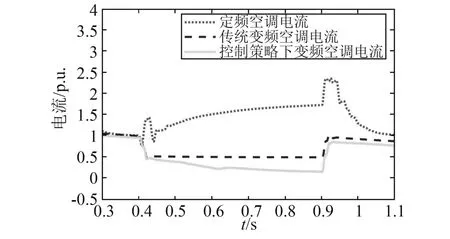
图5 电压跌落至额定电压的70%并持续0.5s的电流

相对于定频，传统变频和自由控制策略下的空调在电压跌落瞬间电流跌落至接近零的某个值，这是因为逆变与整流电路之间存在大电容，自主控制策略的转速下降导致消耗比普通变频消耗更小，因此自主控制策略下的变频空调比传统变频空调二极管关断时间更长，运行时电流更低。在故障切除瞬间，定频空调、传统变频空调以及改进变频空调电流都突增，改进变频空调电流略低于前两者，低压控制策略的变频空调采取了电机转速缓慢恢复的方式，目的是避免过大电流冲击。

从图6可以看出系统电压跌落后，无论是传统变频空调还是自主控制策略下的定频空调，有功功率消耗都明显小于定频空调，自主控制策略下这一优势更明显，同时由于不可控整流器的作用，变频空调有功降为零待解除电压故障后，自主控制策略变频由于转速延迟恢复，有功功率的瞬时冲击远远低于定频空调。

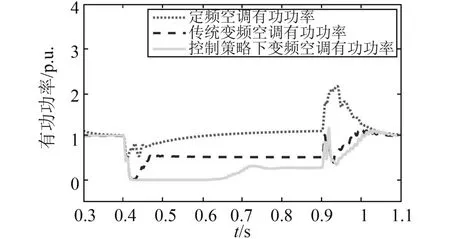
图6 电压跌落至额定电压的70%并持续0.5s的有功功率

由图7可知，无功功率方面变频空调先跌至零，再维持在一个接近于零的常数不变，由于整流桥和逆变器之间存在大电容，当t＝0.4s电网电压下降至额定值的70%时，电容开始放电，直流母线电压开始逐渐降低。此时自主控制策略下电压跌落时变频空调自动降低了电机转速，这种方法可以有效延缓电机失速，从而降低了电机“堵转”的发生率。

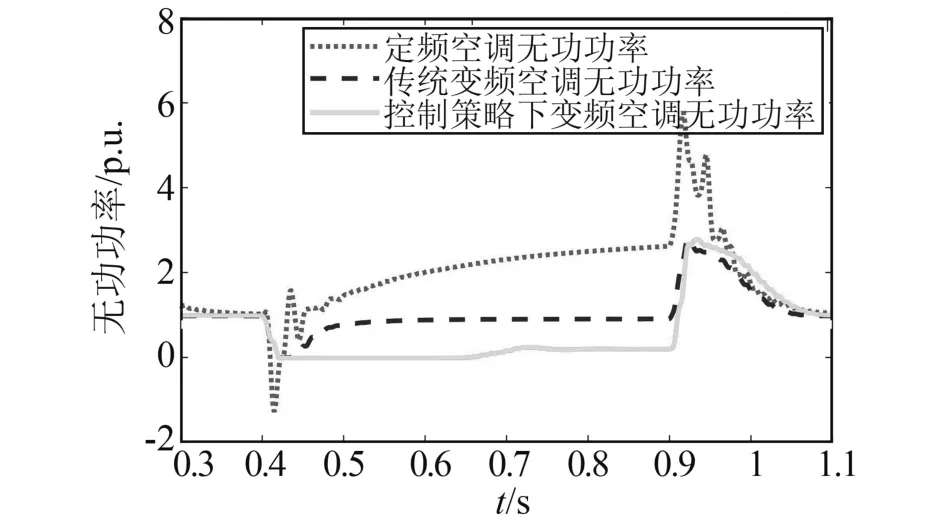
图7 电压跌落至额定电压的70%并持续0.5s无功功率

4 结束语

本文首先对空调负荷运行特性做了深入分析，建立空调负荷等效模型，并系统性提出变频空调在电压跌落以及电压恢复等情况下的自主控制策略，最后在Matlab／Simulink仿真结果表明：自主控制策略下的变频空调无论在电流、有功功率还是无功功率曲线中的动态性能，都好于普通定频空调和传统变频空调的特性曲线性能。本文提出的自主控制策略为研究其他电机驱动类温控负荷及其对电压稳定性的影响奠定了基础，为改善其他负荷特性提供了新思路。