基于挠度影响线差值曲率的简支梁损伤识别研究

李 萌, 张德伟, 刘润州

(安徽建筑大学土木工程学院 安徽 合肥 230601)

0 引言

随着城市交通的发展,桥梁身为城市交通重要基础设施,保证其安全运营是必要的,当桥梁服役达到一定年限时,自身结构会由于材料老化、疲劳效应等一系列因素产生损伤。一旦桥梁发生损坏,将会造成巨大的人员伤亡和经济损失,因此在桥梁的实际运营中进行快速损伤识别和评估是尤为重要的。

现阶段,针对不同桥型的桥梁损伤识别有不同方向的研究。周宇等[1]基于应变影响线差值曲率对无铰拱进行损伤识别。唐盛华等[2]基于支座反力影响线进行曲率差分对梁桥进行损伤识别研究,为桥梁的损伤识别提供了更多的方法和方向。

目前桥梁检测的方式分为两类:利用各种仪器的直接局部观测和采用静动力指标的整体检测,前者为了定位损伤点,往往需要全面检测,工作量大,所以在大中跨桥梁中往往采用整体检测[3],而整体检测中基于频率、振型、模态曲率、柔度矩阵等动力指标的损伤识别[4-6],虽识别精度高,但往往需要大量传感器,布设烦琐。基于影响线的静力指标因少量传感器便可全面反映截面的刚度特性,优势明显,但损伤指标往往难以提取;王新龙[7]对城市简支梁桥损伤识别的挠度影响线法进行探讨和研究;贾亚平[8]利用挠度差值影响线二阶导对连续梁结构进行损伤识别,并通过有损和无损处的曲率比值对损伤程度进行量化;张锦程等[9]通过提出挠度差值影响线二阶导数的连续梁桥损伤识别方法,能够快速识别损伤位置与程度。杜永峰等[10]通过推导挠度随外荷载位置变化的函数在理论上验证并说明了挠度差值影响线用于损伤识别的可行性。

本文推导了梁桥的挠度影响线解析解,在理论上证明了挠度影响线差值曲率(Deflection Influence Line Difference Curvature,DILDC)指标可用于简支梁的损伤识别,并通过数值模拟验证了此指标在工程中的可行性。实际工程中,在梁桥的跨中位置布置传感器或采用非接触式挠度影响线采集仪进行数据采集,对获得的挠度影响线时程响应进行影响线识别,进而获得准静态挠度影响线,可为梁桥的设计计算与健康评估提供理论支撑与思路借鉴。

1 理论推导

简支梁模型如图1所示,基于平衡方程,列出简支梁任意截面的弯矩表达式,由公式(1)可知,梁截面的弯矩表达式与外荷载P的作用位置有关。

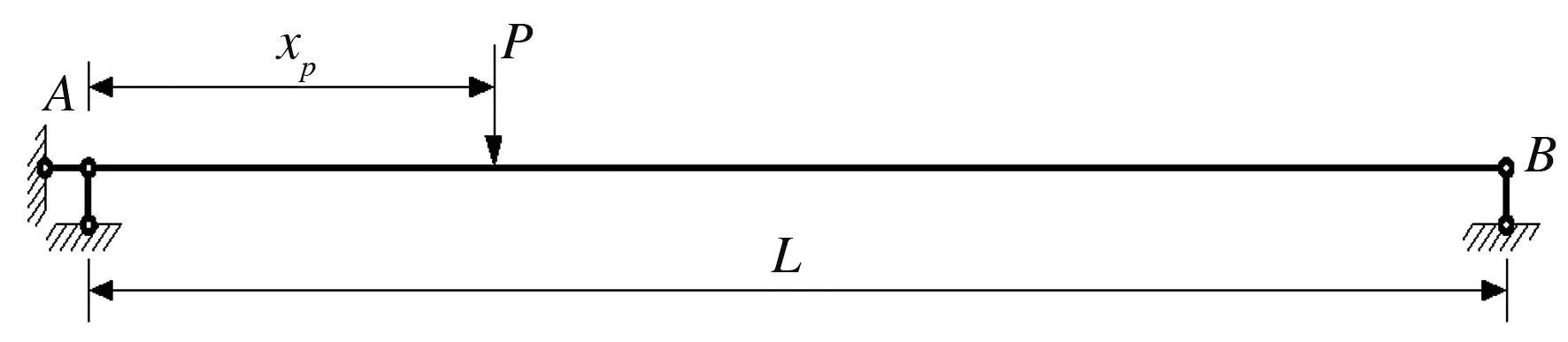
图1 简支梁模型

(1)

由虚功原理可知,在简支梁任意截面处的位移实际上是外荷载所引起的,为表示某一截面处的位移,采用单位荷载法,在此处施加一个向下的单位荷载P=1,并列出对应的内力方程。在此虚设单位荷载作用下简支梁任意截面的弯矩表达式

(2)

其中a为单位荷载到A端的距离,L为简支梁跨长,xp为外荷载到A端的距离。

由莫尔积分公式可知

(3)

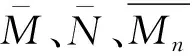
由于弯曲变形在简支梁的位移中占比较大,而剪切变形和扭转变形占比较小,因此剪切变形和扭转变形对位移产生的位移可以忽略不计。

故有简支梁的广义位移公式

(4)

由图2所示,[b-ε,b+ε]区间为损伤区段,当荷载分别作用在简支梁4个部位时,所展现的表达式并不同,因此需要将简支梁分成4段,分段表达。

图2 损伤简支梁模型

由式(1)至式(4)可得,无损简支梁结构的在4个区段的表达式为

当0≤xp≤a时

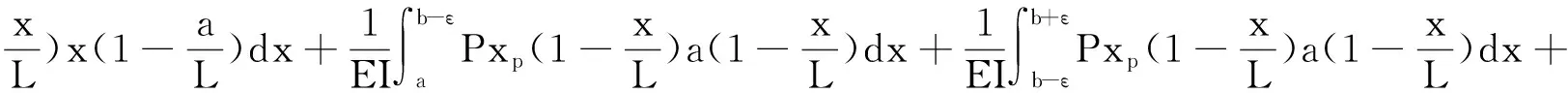
当a≤xp≤b-ε时

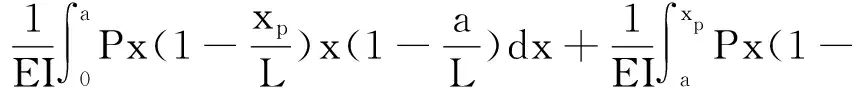
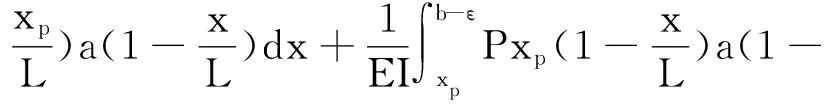
当b-ε≤xp≤b+ε时

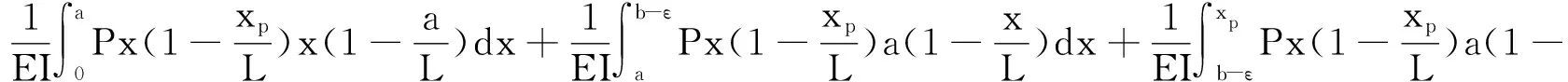
当b+ε≤xp≤L时

当简支梁结构受损时,结构弹性模量降低[11],故将受损区域位移表达中的EI替换为E′I即可表示损伤时简支梁结构不同区段的位移情况,因篇幅限制,则不一一列举。

2 损伤识别

通过对无损结构与有损结构的挠度影响线表达式作差后再求二阶导,得到挠度影响线差值曲率指标,该指标用于反映挠度影响线曲率的变化情况,将挠度影响线差值曲率进行滑动平均处理,可达到放大差异的效果,进而能够实现快速确定损伤位置的目的。有损结构与无损结构的数学表达式差异在系数中体现,因此在简支梁结构上的不同区段具有不同的表达式,运用数学软件将4个区段上挠度影响线作差的表达式积分后进行两次求导,如下式所示。

当0≤xp≤a时

(Δ-Δ′)″=0

当a≤xp≤b-ε时

(Δ-Δ′)″=0

当b-ε≤xp≤b+ε时

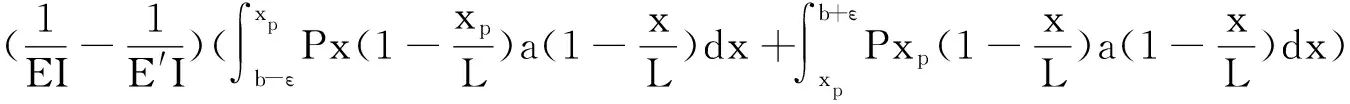
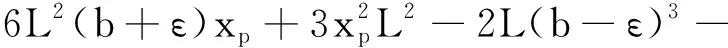
2(b-ε)3xp-2(b+ε)3xp]}

当b+ε≤xp≤L时

(Δ-Δ′)″=0

简支梁结构损伤前后的挠度影响线差值在移动荷载处于无损区段(0≤xp≤a、a≤xp≤b-ε以及b+ε≤xp≤L)时的曲率为0,而当移动荷载处于损伤区段(b-ε≤xp≤b+ε)时的挠度影响线差值曲率不为0,在挠度影响线差值曲线图上会出现突变情况,因此可判断损伤位置。

3 数值模拟

采用MIDAS/Civil建立有限元模型算例,现有简支梁结构如图3所示,材料采用C40混凝土,简支梁跨长L为60 m,划分单元长度为1m,共60个单元。采用降低单元弹性模量的方式模拟单元损伤,通过设置单点损伤和多点损伤工况,进而模拟并验证挠度影响线差值曲率损伤识别效果,采取不同程度的弹性模量降低方式,对20#单元进行不同损伤程度的模拟,测点选取30#单元,具体损伤工况如表1所示。

表1 损伤工况

图3 有限元模型

结果如图4、图5所示,在单点损伤和多点损伤的情况下,挠度影响线差值曲率具有良好的识别效果,在图4中,在20#单元处存在明显的突变现象,在图5中20#和40#单元处存在突变现象,且单点损伤和多点损伤的识别效果均与损伤程度大小有关,损伤程度越高,识别效果越好。

图4 单点损伤

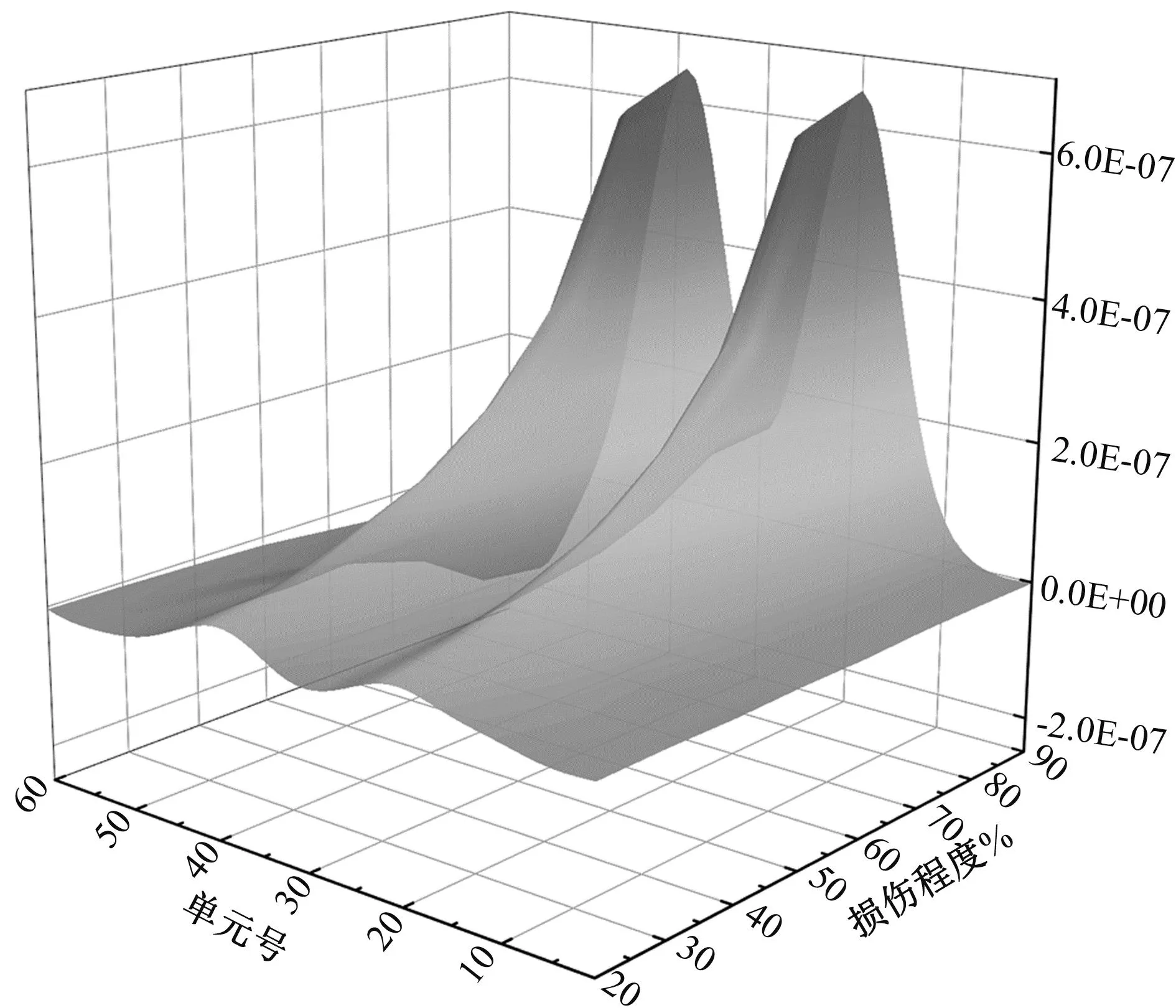
图5 多点损伤

4 结论

本文通过理论推导和有限元验证,说明了挠度影响线差值曲率可以准确定位损伤位置,在桥梁健康监测中具有工程实用价值。

(1)通过滑动平均法处理有限元模型模拟出的数据,可以达到一定程度的消波作用,处理后的数据生成的图像突变更加明显,从而方便找出损伤位置。

(2)挠度影响线差值曲率对简支梁结构的损伤具有较好的识别效果,并且损伤程度越大,损伤识别的效果就越好,因此挠度影响线差值曲率指标具有工程实用价值。

(3)在桥梁结构健康监测中,挠度测量相对容易,数据获得较为便利,通过位移长期监测系统或者借助非接触式挠度测量仪均可获取,并且可以通过单个测点对全桥进行监测,操作方便且较为经济。

(4)通过理论公式推导出无损伤时简支梁桥结构的挠度影响线,与实测桥梁挠度影响线作差后求二阶导,可通过峰值所在位置确定损伤位置。