倒U型双塔连体结构地震反应数值模拟分析

朱伟杰,雷庆关

(安徽建筑大学土木工程学院 安徽 合肥 230601)

在当下经济飞速发展的时代,人们对建筑的造型提出了更严格的要求,除了满足使用需求外,人们更关注建筑的整体效果。高层建筑以独特的造型和功能而受到人们的推崇,然而,目前许多高层建筑仍存在着一些问题。建筑形状不规则而结构复杂的建筑是当代建筑发展的新趋势。但是地震对高层建筑物的震害研究表明不规则的结构形式在面对地震时更容易遭到破坏,且损坏较为严重[1-3]。目前国内外对于单平面不规则形式结构研究颇多且应用广泛,对于双塔连体结构研究较少,因此本文利用SAP2000 软件分别建立了加入X型支撑的两种模型,对其采用了模态、反应谱和时程分析,得出了该模型固有的动力特性,分析了该模型抵抗地震作用影响的能力,为今后的设计提供一定的理论基础[4]。

1 模型建立

本文建立的模型是12层倒U型混凝土双塔结构,每层楼高是3.3 m,共36.3 m,楼面板厚是100 mm,材料是C30混凝土,钢梁采用 Q235钢。结构的水平横向有8跨,竖向有3跨。楼层荷载: 恒载 4.0 kN/m2,活载2.0 kN/m2。地震烈度为8度(0.20 g),地震最大影响系数取为0.16,阻尼比取为0.05,场地的类别是Ⅱ类,设计的地震分组为第二组,特征周期值取0.40 s,抗震等级为Ⅱ级。

用SAP2000 软件建立模型,首先是不加入支撑的原模型A(如图1),第二个是在竖向3跨的中跨位置加入X型支撑的模型B(如图2),第三个是将支撑设置在竖向3跨的两边跨位置的模型 C(如图3 )。

图2 模型B加入X型支撑模型

图3 模型C加入不同位置X支撑模型

2 地震反应分析

2.1 模态分析

模态分析在振动领域应用较为广泛,在模态分析中,一方面,它可以得出结构的相关参数,另一方面,也能准确地对结构做出评估,从而了解结构在地震作用下的响应,方便更好地采取措施来增强结构的稳定性能。特征向量法和Ritz向量法最为常见,其中特征向量法往往会忽略结构的荷载,导致模型精度不高,故本文使用Ritz向量分析法[5]。通过模态分析得出模型A、B、C的前15阶自振周期、质量参与系数,进一步分析结构的各项特性是否符合规定要求。用SAP2000对模型A、B、C进行模态分析后得到前15阶自振周期和质量参与系数,所得数据见表1至表3。

表1 模型A的自振周期、质量参与系数

《建筑抗震设计规范》[6]指出,结构的第一、第二以及第三阶振型最重要,为分析结构的平动、扭动属性,本文取用前三振型的质量参与系数并对其进行分析和判定(见表1至表3),得出如下结论:(1)结合表1数据分析可知,模型A的振型: 第一振型主要是沿着Y方向的平动(UY=0.795),第二振型主要是沿着X方向平动(UX=0.801) ,第三振型主要是沿Z方向的扭动(RZ=0.797)。 (2)结合表2数据分析可知,模型B的振型: 第一振型是沿着Y方向平动(UY=0.790) ,第二振型是沿着X方向的平动(UX=0.800) ,第三振型是绕着Z方向的扭动(RZ=0.790)。 (3)结合上表3列出的数据分析可知,模型C的振型: 第一振型是沿着Y方向的平动(UY=0.790) ,第二振型是沿着X方向平动(UX=0.790),第三振型是沿着Z方向的扭动(RZ=0.790)。 (4)《建筑抗震设计规范》[6]规定了结构的质量参与系数之和应不小于90%。由表1至表3可得出原模型的Sum(UX)和Sum(UY)为0.999和0.999,而模型B、C的Sum(UX)和Sum(UY)均为1,均符合要求。

表2 模型B的自振周期、质量参与系数

表3 模型C的自振周期、质量参与系数

2.2 反应谱分析

反应谱分析指的是先用动力学的分析方法对线性结构进行地震响应分析,后借助统计学的方法画出反应谱,再对线性结构进行分析,最后再用静力学的计算方法来分析结构的地震响应和动力性能[7]。使用SAP2000 对3个模型进行反应谱分析,得到3种模型的楼层位移和层间位移角数据,整理后的数据见表4、图4及图5。根据表4及图4、图5可得出以下结论。

表4 反应谱下3种模型的楼层位移和层间位移角

图4 反应谱下3种模型层间位移

图5 反应谱下3种模型层间位移角

(1) 由表4数据可知,模型A的最大楼层位移是30.118 mm,在顶层,最大层间位移角为1 /899,在第三层; 模型B的楼层最大位移是24.458 mm,相比模型A降低了18.79% ,最大层间位移角为1/1163,在第三层; 模型C最大位移为20.452 mm,相比模型A降低了32.09% ,最大层间位移角为1 /1376,在第四层; 由规范[6]可得,高层结构位移角限值为1/550,3个模型的最大位移角都不大于1 /550,所以符合要求。

(2) 由图4和图5可知,3个模型的层间位移整体都是上升趋势,不同的是它们上升的幅度各不相同。原模型A上升最快,位于3条曲线的最上方,其次为加入X型支撑的模型B ,模型B的层间位移效果与模型C相似,但是模型C上升最慢。3个模型的层间位移角表现出先局部上升,后一直下降的趋势,在前3层上升较快,其中,原模型A的层间位移角上升速度最快,增设X支撑后的模型B、C的各楼层的层间位移角有明显降低,B、C的位移角较为接近且都小于模型A的位移角,说明结构的稳定性得到了提高。

3 时程分析

时程分析法是计算时程波中的不同质点在不同时刻下的s、v以及a来显示出荷载的方向和产生的影响,它是一种直接对动力进行计算的一种方法[8-9]。一般情况下通过分析,时程分析在计算过程中比反应谱计算的结果更为准确、误差更小,能够较为精确地校核结构较为薄弱的那层[10-11],以此来防止结构在地震作用下发生损伤和破坏,使用SAP2000进行时程分析时,本文选用了3种地震波来检测结构的抗震性能,它们是:Taft波(峰值175.9,步长0.02 s) 、Tangshan波(峰值55.49,步长0.01 s)、Lanzhou波(峰值196.2,步长0.02 s)。通过时程分析法,得出3种模型的层间位移和层间位移角(见表5至表7)。

表5 Taft波下3种模型的楼层位移和层间位移角

表6 Tangshan波下3种模型的楼层位移和层间位移角

表7 Lanzhou波下3种模型的楼层位移和层间位移角

(1)由表5至表7可知,3种模型在Taft波下各楼层最大位移分别为22.304 mm、19.617 mm、16.812 mm,最大层间位移角分别为 1/918、1/1569、1/1465,3种模型在Tangshan波下各楼层最大位移分别为58.887 mm、38.006 mm、38.540 mm;最大层间位移角分别为1/553、1/798、1/715;3种模型在Lanzhou波下各楼层最大位移分别为20.239 mm、9.090 mm、7.195 mm;最大层间位移角分别为1/1355、1/798、1/3107,均满足规定。

(2)由图6至图11得,3种模型在Taft波、Tangshan 波和Lanzhou波下的各楼层最大位移都呈上升趋势,模型A的层间位移最大,但在加了支撑之后,层间位移都明显减小,说明结构的稳定性得到了提高,模型B和模型C虽然改变了加入支撑的数量和位置,但是他们的最大位移相差不大。

图6 Taft波下3种模型层间位移

图7 Taft波下3种模型层间位移角

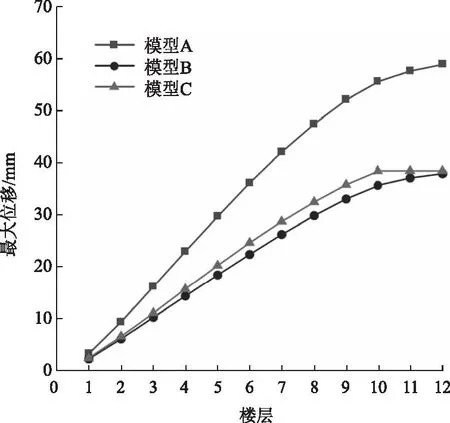
图8 Tangshan波下3种模型层间位移

图9 Tangshan波下3种模型层间位移角

图10 Lanzhou波下3种模型层间位移

图11 Lanzhou波下3种模型层间位移角

(3)由图6至图11得,3种模型在Taft 波、Tangshan波和 Lanzhou 波下的各楼最大层间位移角呈先上升后下降的趋势,其中在Taft波和Tangshan波下,模型B的位移角略小于模型C的位移角,在 Lanzhou波下,模型B的位移角微大于模型C的位移角,从位移角图中可以看出,加了支撑的模型的位移角明显减小,即有支撑体系的模型能有效降低结构的层间位移角,具有良好的抗震效果,但是在Taft波下的模型B的位移角在8到10层发生了突变,位移角值大于模型A,分析导致突变的原因可能是刚度的提高。

4 结论

本文通过使用SAP2000建立模型对倒U型双塔连体结构进行了模态分析、反应谱分析以及时程分析,通过分析得出如下结论:

(1)通过模态分析,3个模型的第十五振型的累计质量参与系数都是大于90%,符合要求。

(2)在反应谱分析中,原模型A的楼层的最大位移和位移角都相对较大,增设X支撑后,它的楼层最大位移和层间位移角都发生了显著的下降,但是改变加入支撑的数量和位置之后,他们的最大位移和位移角相差不大,实际工程可以综合考虑成本等因素去选择加入支撑。

(3)对3个模型的时程分析结果进行对比后发现,在对结构加入X型支撑后,在不同地震波作用下各楼层的层间位移均发生了明显减少,但是它们的层间位移角图有稍微差别,尤其在Taft波下,层间位移角有略微的波动,因此在实际项目中应该尽量多地去选取时程曲线进行计算分析,以此来保证建筑物结构的安全性与稳定性。