基于SLP和遗传算法的车间布局优化

冷护基, 单 恒, 孙 艳, 郑博文

(安徽工业大学管理科学与工程学院 安徽 马鞍山 243032)

设施布局规划是企业发展的重要部分,布局规划的优劣会对企业的生产效率、物料周转效率、工厂设备利用率和物料处理成本等产生重大影响。因此,科学合理的设施布局在车间物料搬运的整体管理成本方面可以减少10%～30%[1]。如果能通过科学合理的设施布局,大幅降低这一成本,就相当于为企业创造利润,从而促进企业的长期发展[2]。

目前,针对车间设备布局有两大主流方法,系统布局规划 (SLP) 和遗传算法。美国工业工程师缪瑟提出的SLP法被广泛应用于汽车制造和其他制造企业的生产研究[3]。一些国外学者对SLP和物料处理分析(SHA)方法应用过程中产生的岗位相互关系图和物料处理图进行了广泛的研究[4-6]。邓兵等人将SLP和遗传算法相结合来优化设备布局模型,该方法降低了材料处理成本,提高了生产车间的利用率[7]。琚晶晶等人开发了一种基于人机工程学的车间布局优化模型,使用传统的SLP和遗传算法对模型进行优化和求解,并通过实例进行了验证[8]。大量研究表明,SLP是较为成熟的解决仓储中心布局的方法,但该法具有主观性,易受研究人员经验的影响,所以需要与其他优化算法结合做定量分析。本文通过将SLP法与遗传算法相结合对A公司车间布局做优化研究,实现了二者间的优势互补,使得车间设备布局更具实用性。

1 SLP求解生产车间的初始布局

1.1 A公司激光切割机生产车间简介

A公司主要生产流程分为生产阶段、正式生产阶段、生产完成和质检包装4个阶段。

正式生产过程在生产作业区进行,包括4个阶段:机床钢板焊接、机床整体加工、主要部件组装、质量检验和包装。车间原始布局图见图1。

图1 车间原始布局图

1.2 物流关系与非物流关系分析

车间物流强度由工艺路线和物流量决定。根据作业单位间的运输频率,将物流关系强度划分为5个等级,运输频率越高,物流关系程度等级越高,常用A、E、I、O、U表示,其程度由强到弱。根据A公司激光切割机生产车间各作业单位间的物流距离和物流强度,得到作业单位间物流关系(见图2)。

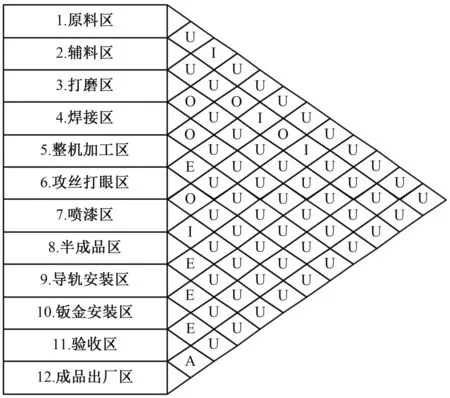
图2 作业单位间物流关系图

在规划车间设施布局时,不仅要考虑物流关系的影响,也要考虑非物流关系对生产的影响,主要包括作业流程的连续性、物料搬运的重量、搬运方便、管理方便等,以此确定作业单位的非物流关系(见图3)。

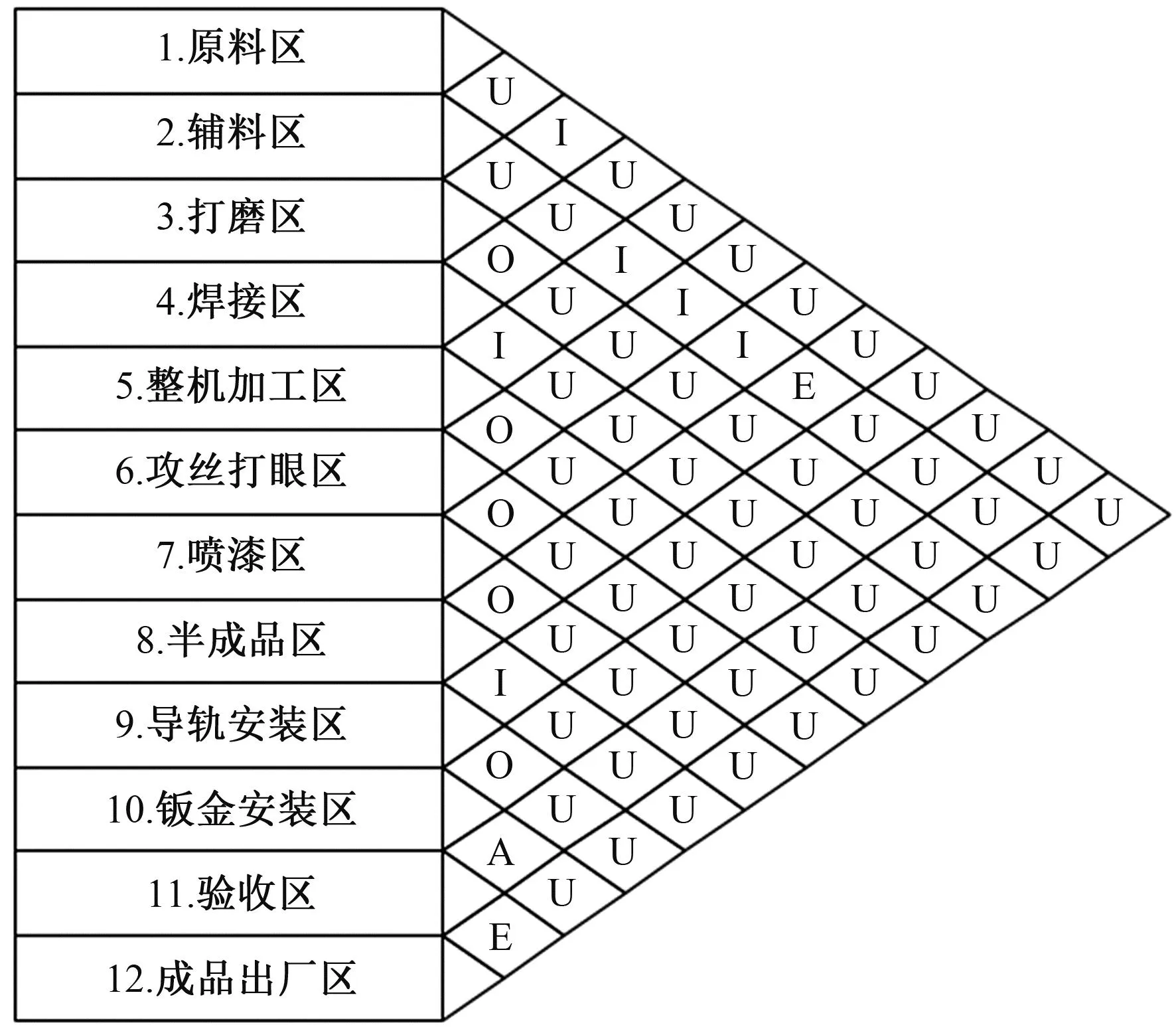
图3 作业单位非物流关系图

1.3 综合关系和初始车间布局

在分析了 A 公司生产车间内各操作单元之间的关系后,需确定它们之间的综合相互关系。步骤为:

(1) 确定物流和非物流关系的权重比。物流关系和非物流关系的权重比通常在1/3到3之间,既要考虑物流关系,也要考虑作业单元之间的非物流关系。因此,本文选取的权重比为m∶n=1∶1。

(2)量化紧密程度。为了量化紧密程度,我们指定每个级别对应的比例。

(3)计算综合相互关系值。用Di和Dj代表任意一对经营单位,用MLij和NLij代表物流关系和非物流关系的量值,综合相互关系密切程度值TLij=mMLij+nNLij。

(4)确定综合相互关系的密切程度。在求出TLij的值后,我们用各层次的比例来确定经营单位之间的综合关系水平。

综合关系分析是对车间作业单位间物流关系和非物流关系进行加权计算,利用数值大小表示两者对车间的综合影响程度。取物流因素和非物流因素比重为1∶1。A、E、I、O、U对应值分别为4、3、2、1、0,加权计算得到作业单位综合相互关系图和初步布局图(见图4和图5)。

图4 作业单位综合相互关系图

图5 生产车间布局图

2 基于SLP和遗传算法的车间布局优化

在设备布局应用中,通过SLP法对车间物流和非物流因素的定性分析,对生产线的物流状态做出系统性的分析,从而得到较为合理的初步布局方案。SLP法注重工艺的连续性和车间布局的合理性,对车间设备布局优劣性的判断过于依赖设计人员的经验,缺乏对车间的定量分析,导致无法直观、科学地判断出布局是否最优。因此,建立加工车间数学模型,以物流成本最低和非物流关系密切程度最大为目标,设计遗传算法,通过MATLAB进行编写求解,促进公司的长期可持续发展。

2.1 A公司激光切割机生产车间问题的数学模型

2.1.1 模型假设

本文旨在优化A公司生产车间的布局,最大限度地提高操作单元的效率,同时使物料搬运成本最小化。为了实现这一目标,根据设施布局理论和这两个目标建立了一个布局优化模型。模型假设为:

(1)为了简化生产车间的面积,采用已知长度和宽度的矩形块结构,坐标系的原点为车间的左下角。X轴正半轴作为工厂的长边方向,Y轴正半轴作为工厂的宽边方向;

(2)所有工作单元都位于同一平面上;

(3)将各单元都简化为矩形,其边分别与X轴和Y轴平行;

(4)每个单元的中心点作为其入口和出口点;

(5)不同作业单元之间的单位运输成本大致相等。

通过使用这个模型优化生产车间的布局, A公司可以改善作业单元之间的非物流关系,使材料处理成本最小化。A公司生产车间布局坐标见图6。

图6 生产车间布局坐标图

2.1.2 构建目标函数

基于A公司激光切割机生产车间布局实际情况,目标函数的对象为物流成本最小和非物流关系最大。

设i和j为布局方案中的作业单位,d为两个作业单位之间的距离,f为两个作业单位之间的搬运量,C为单位物流成本,则物料搬运成本函数的表达式

(1)

对于非物流函数,以非物流等级为权重引入距离关联量化因子,得到非物流关系函数表达式

(2)

C1表示非物流关系总值,T代表非物流关系强度等级,b代表关联因子。

其中关联因子量化值如表1所示。

表1 关联因子量化值

其中,dmax指的是生产中心规划区域长和宽的长度之和。

为了求解方便,将其转化为单目标函数。根据布局侧重点,确定函数的赋权值V,函数赋权值为V1,函数赋权值为V2,其中V值固定为1,V1值为2/3,V2值为1/3。

V=V1+V2=1

(3)

所以最终的目标函数是

minC=V1C′1-V2C′2

(4)

2.1.3 约束条件

车间布局的设计通常是在车间的特定区域内进行。在设计过程中,要考虑到各种因素,如实际条件和公司要求。该生产中心的约束条件和设计要求如下。

(1) 作业单位不重叠

(5)

(6)

(2) 边界限制

(7)

(8)

其中,L和W分别代表生产车间面积的长与宽,Li和Wi分别代表作业单位i的长和宽,同理Lj和Wj代表作业单位j的长和宽,Δxij和Δyij分别代表作业单位i和j之间的横向距离和纵向距离。以上约束条件将在遗传算法中利用惩罚函数等策略加以限制。

2.1.4 初始化群体

在开始计算之前,遗传算法需要生成一定数量的种群,以方便后续操作。在种群智能算法中,种群太多会导致计算时间增加,收敛不稳定,效率降低;而种群太少会导致种群内缺乏多样性,导致次优的结果。为了防止这种情况,可以通过将SLP法得到的初始布局规划方案与随机生成的个体相结合,手动调整初始种群,创造一个多样化的最佳初始种群。

2.1.5 适应度函数

适应度函数,也被称为评价函数,适应度值越高,个体被选作父母的机会就越大,存活下来,并将其有利的特质传给后代,适应度值较低的个体被淘汰的可能性就大。这个过程确保了理想的性状不断被继承,最终形成最佳的个体解决方案。在该案例设施布局过程中,出现了数个约束以及目标函数,根据数学模型,并利用取倒数法形成适应度函数。

本文研究的是最小值问题,采用第一种处理方式,所以目标函数为

(9)

其中,

f(x)=C′1-C′2

(10)

G=1000

(11)

G为惩罚函数,1000为惩罚因子。

2.1.6 交叉与变异

遗传算子是遗传算法的一个重要组成部分,它模仿自然选择来选择最合适的个体。它由4个基本操作组成:选择、交叉、突变和变异。本文用了实数编码方式,选择部分交叉和单点变异。部分交叉是指叉点选取一部分基因相互交换;单点变异是指个体基因序列中每一个基因进行变异,以某一个小概率来代替个体基因对上的原基因。

2.2 模型算法求解

通过MATLAB编写和运行遗传算法程序,部分代码如图7所示,运行结果如图8所示。

图7 部分代码图

图8 粒子迭代过程

从图8可以看出,最优作业单位坐标分别为 (44,26)、(44,14)、(55,23.5)、(55,16.5)、(58.5,7)、(41.5,4.5)、(23.5,4.5)、(28.5,23.5)、(10.5,16.5)、(10.5,23.5)、(8,7)。

根据最优单位坐标和面积要求画出优化后的布局图(如图9所示)。

图9 优化布局图

3 结果分析

为检验设施布局优化后的效果,A公司车间布局优化前后作业单元距离及运量如表2所示。

表2 作业间物流关系

由表2可知,优化前的总物流距离和为294 m,优化后的总物流距离和为244 m。优化前的总物流量距积和为7483,而优化后的总物流量距积和为6545。优化后的方案总物流距离和减少了50 m,优化比例约为17%;总物流量距积和减少了938,优化比例约为12.5%。

4 结论

本文以A公司的生产车间为研究对象,通过SLP法制定了车间布局的初步改进方案,并结合遗传算法对初始车间布局方案进行了优化。结果表明新的方案不仅降低了物流和运输成本,而且还改善了运营单位之间的密切关系,能够有效帮助A公司提高生产车间的效率。