基于TLS-ESPRIT算法和选择模态法的模型降阶研究

付江涛, 杨毅强, 蒲 维, 宋 弘

(1.四川轻化工大学自动化与信息工程学院 四川 自贡 643000;2.人工智能四川重点实验室 四川 自贡 643000; 3.阿坝师范学院 四川 阿坝 623002)

0 引言

目前,高增益励磁系统在电力系统中应用广泛,但随之出现的低频振荡也成为电力系统稳定运行的一大瓶颈,设计合适的阻尼控制器是提升系统稳定性的重要措施[1]。广域测量系统(WAMS)的发展为广域阻尼控制器(wide area damping control,WADC)的设计提供了基础。WADC与传统的PSS相比,可以在宏观上对系统进行控制,脱离本地信号的局限。为设计合适的阻尼控制器,需要全面了解系统的动态特性。但在实际的电力系统中,系统的全阶模型难以得到,而且模型的阶数较高,容易出现“维数灾”问题,也不利于后续的分析与设计[2]。故在辨识模型与系统主模态相同的条件下,如何设计一个低阶系统与待辨识系统有着同样的频率响应特性,如何在确保模型精度的情况下实现系统降阶仍需深入研究[3]。

系统辨识的主要思想是通过传递函数来对系统进行表征[4]。在研究系统的过程中,准确的系统辨识有着举足轻重的地位。1950年便出现了最早的系统辨识,但由于理论不成熟,仅在线性系统中适用,对于非线性系统的适用性较差[5]。近年来,随着计算机的性能以及优化算法、遗传算法等概念的发展,许多系统辨识的方法在非线性系统中也受到青睐。

在系统辨识的过程中,模型的阶数过高会增加系统的复杂度和计算难度。为了更准确地进行系统辨识、简化后续分析的难度,对模型进行降阶处理是很有必要的。目前,常见的模型降阶方法有:(1)奇异值分解(singular value decomposition,SVD)方法、平衡截断法(balanced truncation,BT)和交替方向隐式(alternating direction implicit,ADI)截断法,BT方法在中小模型应用较多[6-7];(2) Krylov子空间类似方法:理克雷洛夫算法(rational Krylov,RK)和迭代有理克雷洛夫算法(iterative rational Krylov algorithm,IRKA)[6];(3)模态选择法:通过识别系统的模态,并且将系统的主导模态保留下来的方法[6]。文献[8]和[9]采用模态选择法对系统模型进行降阶处理。文献[6]和[10]分别采用了平衡截断法和交替方向隐式平衡截断法对并网系统和风电场系统进行模型降阶研究。文献[11]和[12]通过使用Krylov子空间方法对高阶系统模型进行降阶。文献[13]和[14]采用特征值分析方法对电机组模型降阶分析。以上的方法从多个角度对模型进行降阶研究,但这些方法存在着计算效率低及降阶模型的变量缺乏实际的物理意义等问题[9]。

针对存在的不足之处,本文通过TLS-ESPRIT算法和选择模态法[15]来对系统进行辨识和降阶处理,将辨识得到的留数和极点重新构成系统传递函数,将系统传递函数进行降阶,使其降阶为低阶系统。在单机系统及IEEE四机系统出现低频振荡的场景下,通过对比系统降阶前后的功率以及角速度的仿真波形的吻合情况,验证方法的合理性和有效性,为后续阻尼控制器的设计奠定基础。

1 系统传递函数的辨识

1.1 TLS-ESPRIT算法

TLS-ESPRIT算法是在ESPRIT算法的基础上进行改进,是用来谐波恢复、衰减振荡信号参数估计的工具[16-17]。与Prony算法相比,该算法在抗噪方面效果显著[18]。此外,TLS-ESPRIT算法在生物信号处理、雷达阵列信号及语音信号等场合也得到了广泛的使用。

假设x(n)是一组正弦信号和噪声信号的组合,正弦信号的幅值是按指数规律变化的,在时刻n,其表达式为

(1)

其中,Ts为采样周期;阶数p为信号实际含有的正弦分量个数的2倍;ci=Aiejθi,Ai、ωi、θi、σi分别表示第i个模态的幅值、角频率、相位和衰减因子;w(n)为噪声信号。

通过采样数据序列x(0),x(1),…x(N-1)可以构成Hankle矩阵

(2)

式中,L>p;M>p;L+M-1=N。

对矩阵X奇异值分解可得

(3)

(2)将M可以划分成4个p×p的矩阵。

(4)

(5)

(4)在得到采样信号中各个分量的频率和衰减因子,通过最小二乘法来解出幅值和初始角信息。对于N点的采样信号

Y=λc

(6)

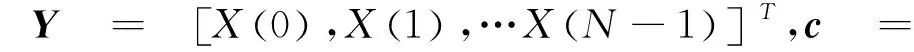
(5)采用最小二乘法可以得到解为留数c=(λHλ)-1λHY,可以得到信号中各个分量的幅值和初始角信息分别为

Ap=2|cp|

(7)

φp=arg(cp)

(8)

(6)通过采用(3)中的λi,可以得到由系统的传递函数的特征值(极点)构成的向量为

P=log(λi)/T

(9)

其中,T为采样时间,i=1,2,…,p。

1.2 系统辨识

假设系统是可控可观测的,状态方程为

(10)

式中,x表示状态向量;y表示输出向量;u表示输入向量;A表示状态矩阵;B表示控制矩阵;C表示输出矩阵。

与之相对应的传递函数为

(11)

式中,Λ=ΨTAΦ是由特征值组成的对角矩阵,对角元素为特征值;Φ为右特征向量矩阵;Ψ为左特征向量矩阵。因为Λ是对角矩阵,因此可以化为

(12)

将TLS-ESPRIT中给出的系统传递函数的留数和极点代入式(12)中,得到系统的传递函数表达式。

2 系统降阶

对于小型的电力系统所得的传递函数相对简单,但是对于大型的电力系统来说,所得到的传递函数阶数高,主导模态可能会被次要模态掩盖,给后期的使用和运算带来许多不便,因此需要在保留主要特征的情况下,将系统的阶数降到一个合理的数值。

2.1 模型降阶的基本条件

在模型降阶的时候,必须满足以下条件:

(2)降阶系统要保留原系统的性质,如稳定性和无缘性;

(3)降阶的算法或者程序简单方便[7]。

2.2 模态降阶法[9]

2.2.1 选择主导模态

模态降阶法首先需要找到主导极点或者主导特征值。主导模态的判别标准为:在复平面中距离虚轴最近的极点为主导模式极点,若存在距离相近的状态,则通过比较阻尼比,阻尼比小的为主导模态。

2.2.2 确定相关状态

采用参与矩阵来表示模态与状态变量的关系,矩阵中的元素Pki=ukivki为参与因子,用来表示第i个模态与第k个状态变量之间的参与程度。

(13)

2.2.3 构造降阶系统

设系统状态方程为

(14)

(15)

其结构框图如图1所示。其中,实线框为相关状态子系统,虚线框为不相关状态子系统,对于不相关的子系统可以表示为

图1 动态系统结构图

(16)

从图1中可以得出,相关状态子系统表达式为

(17)

当t≥t0时,不相关状态变量x2的表达式为

(18)

则相关状态变量x1可以采用主导模式进行表示。

(19)

式中,λi表示主导模式;vi表示对应的特征向量(vi只是相关状态变量的部分);li为常数。将(19)式代入(18)中,可以得出不相关状态表达式为

(20)

不相关状态子系统输出的表达式为

(21)

(22)

式中,M满足以下条件

M*[v1,v2,…,vh]=[H(λ1)v1,H(λ2)v2,…,
H(λi)vi]

(23)

综上可以得出,不相关状态子系统对于相关状态的响应表达式为

yx2=Mx1

(24)

但是需要注意的是,M的存在需要满足条件Vh为满秩矩阵,只有Vh为满秩矩阵时候,M才有唯一的解。如果矩阵不是满秩,则会存在多重解,可以通过附加条件对其进行消除。将式(24)代入式(17)中,可以得出最终的降阶系统

(25)

以上就是系统的降阶模型的全过程,对于输入-输出系统来说,可以对其进行以下的分区操作。

(26)

类似于上述推导构造过程中Ar的降阶方法,可以得出系统降阶后的模型(Ar,Br,Cr,Dr)。其中,

(27)

采用选择模态进行系统降阶主要有两个优点:一方面是降阶后的模型与原系统模型的主导模态保持一致;另一方面是降阶后模型的各个状态变量的物理意义得到了保留,同时也是该方法与平衡截断法等Gramian算法的优势所在。

2.3 本文的总体流程

本文总体的流程可以分为两大部分:系统辨识及系统降阶。具体通过TLS-ESPRIT算法对模型辨识,采用模态降阶法将高阶系统转化为低阶系统,具体流程如图2所示。

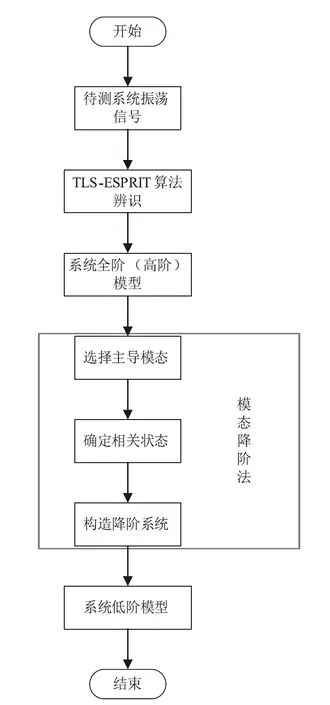
图2 本文总体流程图

3 算例分析

为了验证所提方法的合理性和可行性,分别对单机无穷大系统以及IEEE四机二区域系统进行仿真验证;对于模式未知的模型,对比原模型与辨识后模型的时域仿真波形[20]。

3.1 单机无穷大系统

采用单机无穷大系统,系统由发电机、励磁系统、PSS和无穷大母线组成,阻尼控制器一般以转子角速度差值Δω作为反馈信号,PSS的输出作为励磁调节器的控制信号。将整个单机系统看成黑盒,由小扰动信号作为输入信号,角速度差值Δω作为输出信号构成的单输入单输出系统,单机系统结构如图3所示,其中虚线框中的部分为所需要辨识的部分。

图3 单机系统结构

设置采样频率为50 Hz,通过使用第1节的辨识方法得到一个高阶系统模型,利用模态降阶法将高阶模型转化为低阶模型。为验证降阶后的模型与原来的模型具有相同的动态特性,对单机系统施加扰动信号,大小设置为0.01倍参考电压Vref。原系统与辨识降阶后系统的时域响应如图4所示。由图4可知,辨识降阶后的系统与原系统的动态特性几乎一样,即便存在误差,其量级也很小,说明了辨识后的系统可以代替原来的高阶系统,简化了后续的计算与研究。

图4 单机系统辨识结果

3.2 四机二区域系统

IEEE的四机二区域系统主要由2个区域组成,区域1由发电机G1和发电机G2组成,区域2由发电机G3和发电机G4组成,四机系统的结构如图5所示。通过系统辨识和模态降阶法来对四机系统进行辨识和降阶,本文主要分析区域间功率ΔPe和区域间的转速偏差Δω,原系统与辨识后的系统的时域响应如图6所示。

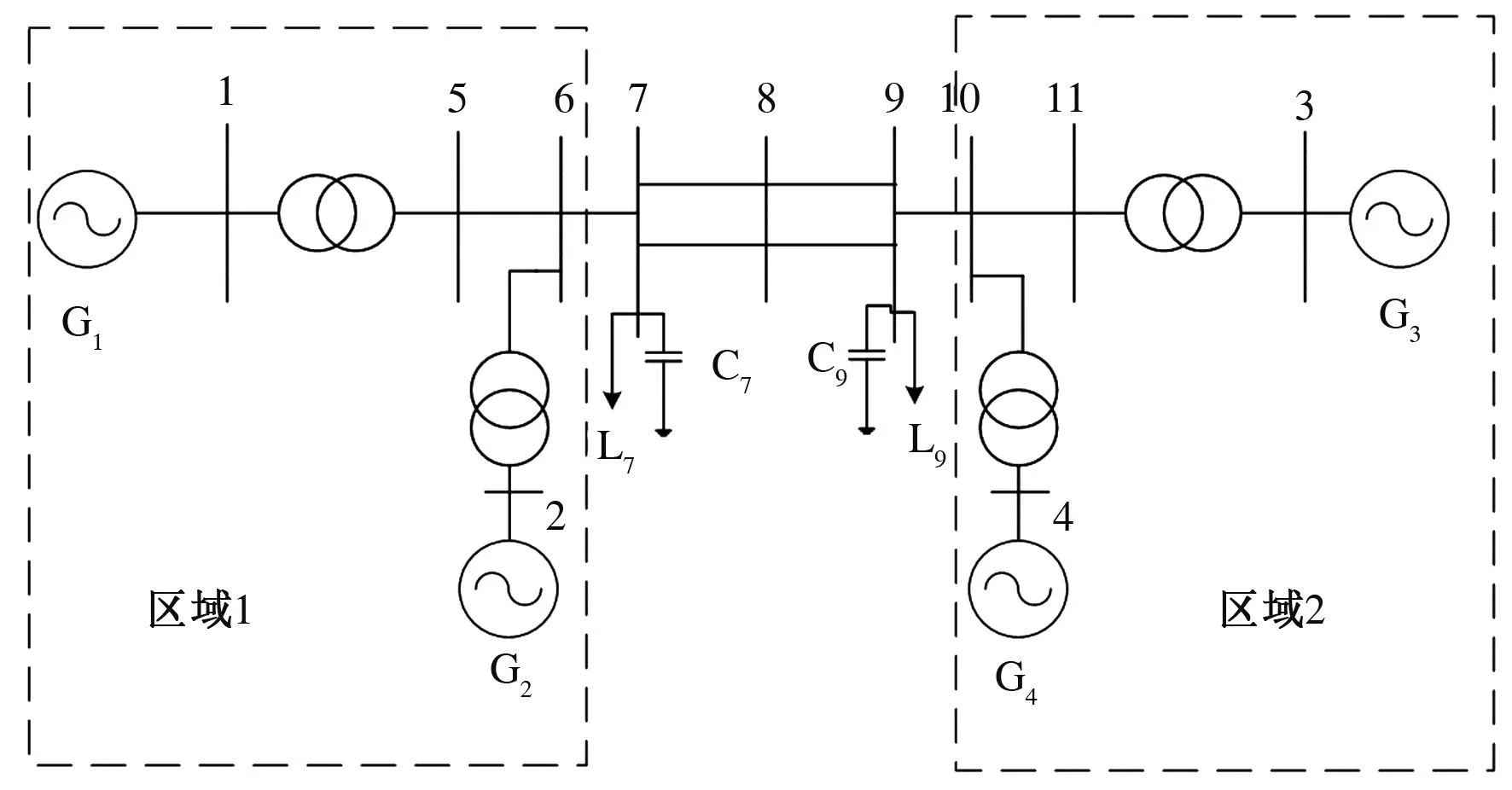
图5 四机系统结构图

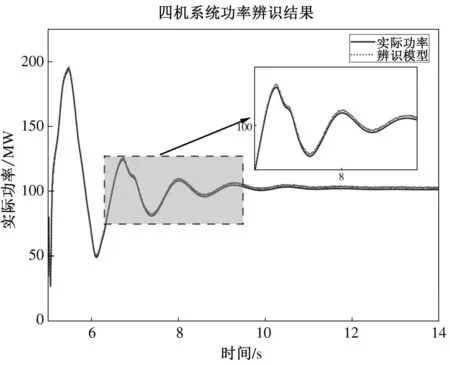
(a) 功率辨识结果

由图6可知,系统原模型的稳态功率为101.5 MW,降阶后的模型稳态功率为102.1 MW,稳态功率之间的误差仅为0.5%。转速偏差也是与之类似,误差较小。原系统与降阶后的系统转速差和功率的曲线几乎相同,也就是说,动态响应误差在可接受的范围之内。误差的主要原因可能是在对非线性系统的线性化和系统降阶过程中存在一定的误差。仿真实验结果表明,降阶后的模型可以较为准确地还原出原系统的稳态和暂态行为,其中所存在的误差在实际工程中是在可接受范围之内的。

3.3 不同方法的ITAE指标比较

采用时间乘绝对误差积分(ITAE)作为衡量降阶系统精度的指标。对于连续的系统来说,ITAE公式为

(28)

由图7可以得出,本文采用的方法精度较高,对于电力系统中的两种不同的电力系统模型,均优于Prony方法和BT方法。对系统的辨识和降阶有着良好的辨识精度,同时也简化了后续研究的运算难度。

图7 ITAE指标对比

4 结论

随着电力系统的不断发展,构建合适的电力系统仿真模型对电力系统的运行有着重大意义。但是对于规模日益增大的电力系统来说,辨识得到的全阶模型对于后续的研究是较为困难的,所以需要对得到的高阶模型进行降阶处理,在保证稳态和暂态行为不变的情况下简化后续的分析。本文提出了基于TLS-ESPRIT算法辨识和选择模态降阶的方法对单机无穷大系统和四机二区域系统进行辨识和降阶分析,仿真分析结果表明:

(1)TLS-ESPRIT算法可以通过系统的输出信号辨识得出系统模型的传递函数,为后续的系统模型降阶奠定了基础。

(2)基于模态选择法降阶后的模型相比于全阶模型,具有相同的稳态和暂态行为,且与其他方法相比,精确度较高。