低碳视角下冷链配送路径优化

闵 聪,桂海霞

(安徽理工大学经济与管理学院 安徽 淮南 232001)

0 引言

2030年实现碳达峰、2060年实现碳中和的目标对高碳行业施加了更多碳排放限制,促使其加大技术改进和科技创新,向低碳经济转型。这一政策对于生鲜品冷链物流这一高耗能、高碳排放的行业尤为重要。如何实现冷链物流运输过程中的节能减排成为了一个亟待解决的行业难题。

生鲜冷链配送路径优化问题可以归结为车辆路径问题(VRP)。目前,学者们从模型和算法两个角度对VRP问题进行了深入研究。张念等[1]构建了约束条件下多车场配送模型,首先使用聚类算法对客户群划分,然后使用改进遗传算法进行仿真求解,降低了总体的配送成本。王力峰等[2]在对冷链物流配送求解时对客户价值等级进行了分类,对客户价值高的优先进行配送。使用遗传算法进行模型求解,降低配送成本,提高客户的满意度。杨柳等[3]对鲸鱼优化算法进行适当改进,并应用于冷链配送模型仿真求解,既实现了低碳配送又降低了配送成本。王智忆[4]等使用蚁群算法构建了以碳排放量最小和总配送路径最短为目标的模型,进一步提高企业的经济和社会效益。张晓凤等[5]详细阐述了灰狼优化算法的搜索机制和实现过程,整理归纳了多位学者的研究方法,并分析了多种改进灰狼算法的特点。康凯等[6]提出了一种结合2-opt局部搜索机制的改进蚁群算法,并用实例验证了模型及算法的有效性。李常敏等[7]在城市物流配送网络模型中以碳排放量、行驶距离和使用车辆数最小为目标建立模型,改进了传统遗传算法求解。李伯棠等[8]利用具有不同重要性和优先级的模糊目标规划法,以物流成本、碳排放量和响应能力为目标,建立了一个闭环物流网络模糊混合线性规划模型。杨玮等[9]结合我国关于碳排放的相关政策,以企业总成本最低为目标,设计并改进了麻雀搜索算法,为冷链物流企业库存-配送优化问题提供了一种新型的解决方法。黄梦涛等[10]用二叉排序树代替传统ARA*算法中用来存储节点信息的线性表,减少算法执行的时间。在路径优化问题求解上,蚁群算法、遗传算法等出现较早,改进算法种类也较多。本文选取的灰狼算法是一种模拟大自然中灰狼群合作狩猎的元启发式算法,算法的优化过程相对较快,在众多领域都有所应用。

针对冷链运输综合配送成本考虑不全面的问题,学者们通常以生鲜度、客户满意度、车辆运输成本最低等为优化目标。虽然部分学者也将碳排放成本作为目标函数的一部分,但大部分只考虑了燃油消耗产生的碳排放成本,而忽略了制冷剂产生的碳排放成本。本文在冷链配送模型中考虑了车辆荷载和装卸时的能源消耗和碳排放,在已有研究的基础上,提出了以碳排放量最低为目标的冷链路径优化模型,并对传统灰狼算法进行了适当的改进,使用python编程软件对冷链配送模型进行仿真求解,对算法和模型的合理有效性进行测验,为冷链物流路径优化的研究提供了新的思路。

1 模型的构建

1.1 问题描述

本文在一定配送条件下,构建以碳排放量最小为目标的冷链配送路径优化模型。碳排放量最小的车辆路径优化问题涉及一个物流配送中心和多辆配送车辆,且满足多个客户的不同需求。研究的目标是寻找碳排放量最低的车辆行驶路径,并尽可能使用较少的车辆。冷链配送车辆较为特殊,在进行配送任务时制冷剂的消耗在装卸货物时有所变动,载重量不同时油耗也有所不同,所以对于碳排放量最小的求解并不是对配送路径最短问题的求解,需要根据构建的模型进一步计算。冷链配送模型有以下假设:只有一个物流配送中心;配送中心和客户需求节点的位置已知;配送中心备货可以满足每个客户的需求量,不考虑缺货情况;车辆在对客户进行配送时不得超过其装载量;每个客户的需求必须得到满足;配送车辆为一种车型,且装载量相同;每个客户只能且必须访问一次;碳排放量与车辆的燃油消耗量成正比,车辆燃油消耗量与车辆行驶距离和载货量有关,随着载货量的变化,单位吨位的货物燃油消耗也不同。

1.2 模型建立

车辆的碳排放量与油耗存在线性关系[3]。冷链配送过程中的碳排放主要包括配送车进行配送活动时燃油和制冷剂消耗产生的碳排放。运输时的碳排放量与油耗成正比关系,碳排放量为车辆负载燃油消耗量与燃油二氧化碳排放系数的乘积。制冷剂的碳排放包括了车辆运输行驶过程中和货物装卸时的碳排放量之和。具体计算公式为

(1)

其中,μ1表示燃油消耗碳排放系数,γ1表示车辆满载耗油量,γ0表示车辆空载耗油量,L表示车辆最大载重,qij表示车辆运输从客户需求点i到j时的载重,μ2表示车辆运输制冷时的碳排放系数,μ3表示车辆装卸制冷时的碳排放系数。

模型的约束条件分析如下。

配送车辆都有额定载重,在执行配送任务时车辆不可超载,表示为

(2)

为了达到节能减排的目的,交叉配送增加能源消耗,所以配送车辆对客户需求点进行配送时只能由一辆车送货且只能一次性完成配送任务,表示为

(3)

配送车辆行驶路径需要从配送中心出发且最终回到配送中心,表示为

(4)

一共有n个客户需要进行冷链配送服务,表示为

(5)

未知参数取值为0或1,表示为

综上所述,建立了以下目标函数为低碳排放量的配送模型。

(i=1,2,…,n;j=1,2,…,n)

2 模型算法设计

2.1 灰狼算法

Mirjalili等人受到了大自然中灰狼群狩猎行为的启发,在2014年提出了基于群体智能的灰狼算法(Grey Wolf Optimizer, GWO)。该算法将优化问题看作是灰狼群体的寻食过程,通过模拟灰狼个体之间的协作和竞争关系来寻找最优解。

每个灰狼个体的位置和速度都不同,位置表示个体的解向量,速度表示个体在解空间中的搜索方向。通过灰狼之间的协作和竞争关系,每个灰狼个体可以根据自身的经验和周围群体的信息调整自己的位置和速度,以便达到更好的解。在灰狼算法中,alpha灰狼、beta灰狼和delta灰狼是3个关键角色,它们代表了群体中的最优解。每个灰狼个体位置和速度的更新都是根据这3种灰狼之间的协作和竞争关系来进行的。

2.1.1 包围猎物

灰狼在狩猎过程中包围猎物,数学建模上可以表示为

(6)

(7)

2.1.2 狩猎

灰狼能识别猎物位置并围攻,α带领β和δ指挥狼群。假设α、β和δ为当前最优解决方案,与猎物距离较近,利用它们的位置确定猎物位置,指挥其他灰狼个体更新位置,并逐步接近猎物。

以下是描述灰狼个体跟踪猎物位置的数学模型。

灰狼与猎物距离更新公式

(8)

(9)

(10)

灰狼位置移动更新公式

(11)

(12)

(13)

(14)

2.1.3 攻击猎物

2.2 算法改进

群体智能优化算法可通过多种方式进行改进,其中常用的策略主要集中于两方面。一方面是改进种群初始化策略,采用更加合理的映射方式降低随机初始化种群分布不均所带来的影响,使种群在初始化阶段尽可能均匀地分布在搜索空间内。这种改进策略有助于种群在进行全局搜索的初期遍历所有搜索空间,从而避免算法遗漏全局最优解。另一方面是针对个体搜索方式和进化策略的改进,标准仿生优化算法的个体搜索策略往往使用相同或线性变化的搜索步长,其缺陷为容易陷入局部最优解,且固定或线性递减的搜索步长无法帮助个体跳出局部极值,从而导致种群出现进化停滞的现象。因此,同时对种群初始化策略和个体搜索策略进行改进可有效提高算法性能。本文采用两种改进策略同时对灰狼算法进行改进。

2.2.1 初始化种群

在群体优化算法中,通常使用伪随机数对种群进行初始化,但这种方法可能会导致种群分布不均,从而降低种群的多样性和寻优速度。标准的灰狼算法通常采用随机方式产生初始化种群,这种方法难以维持灰狼种群的多样性,并且在算法搜索初期难以遍历全部搜索空间,容易陷入局部最优解。为了解决这个问题并保证算法具有全局搜索能力,可以采用混沌映射的方法初始化种群,使初始种群均匀分布在搜索空间内。Logistic和Tent混沌映射方法在种群初始化方面使用较多。本文采用均匀性和迭代速度更为优秀的Tent混沌映射改进标准灰狼算法随机初始化种群的方式。Tent初始化种群可以产生分布较为均匀的初始值,增加初始种群接近最优解的概率,从而加快算法收敛,缩短搜索个体寻找最优解的时间。

(15)

2.2.2 改良收敛因子

WGO的收敛因子由距离控制系数a决定。随着迭代次数的增加,控制系数呈线性递减趋势,这对算法后期的狼群多样性和全局搜索能力有严重影响。为了避免种群被困在局部极值区域,本文对收敛因子进行改进,在算法迭代过程中利用指数函数来衰减a。改进后的收敛因子为

由上式可知,收敛因子a随迭代次数的增加呈非线性动态变化,使用改进的非线性收敛因子可平衡算法的全局和局部搜索能力。前期递减速度慢,有利于全局探索;后期递减速度变快,提高了局部最优解的搜索能力,促进算法收敛。这有助于发现更多全局最优解,提高算法的效率。

2.3 改进灰狼算法

改进灰狼算法步骤如下:

步骤一:初始化搜索个体种群xi(i=1,2,…,n)、a、A和C的值;

步骤二:根据式(15)利用Tent混沌映射结合优化参数的上下界初始化灰狼群位置;

步骤三:计算每一个搜索个体的适应度,xα为最优搜索个体,xβ为第二优搜索个体,xδ为第三优搜索个体;

步骤四:当t小于最大迭代次数时,每一个搜索个体根据式(14)更新位置,更新a、A和C的值,重新计算每个搜索个体的适应度,更新xα、xβ和xδ的值;

步骤五:达到循环迭代次数时,返回xα最优搜索个体。

3 仿真与分析

为了验证算法的有效性,本文模拟冷链配送活动,选取1个配送中心和20个客户需求点。该配送中心为20个门店、超市提供冷链服务。模型中的参数设置如下:冷藏车载重量为7 t,行驶速度为50 km/h,满载耗油量25 L/100 km,空载耗油量15 L/100 km;车辆行驶过程中燃油消耗碳排放系数为3 kg/L,制冷过程中制冷剂消耗碳排放系数为2.5 kg/L。客户点具体地址、需求量和需求时间如表1所示。配送中心序号为0,客户需求点依次排序(1,2,…20)。

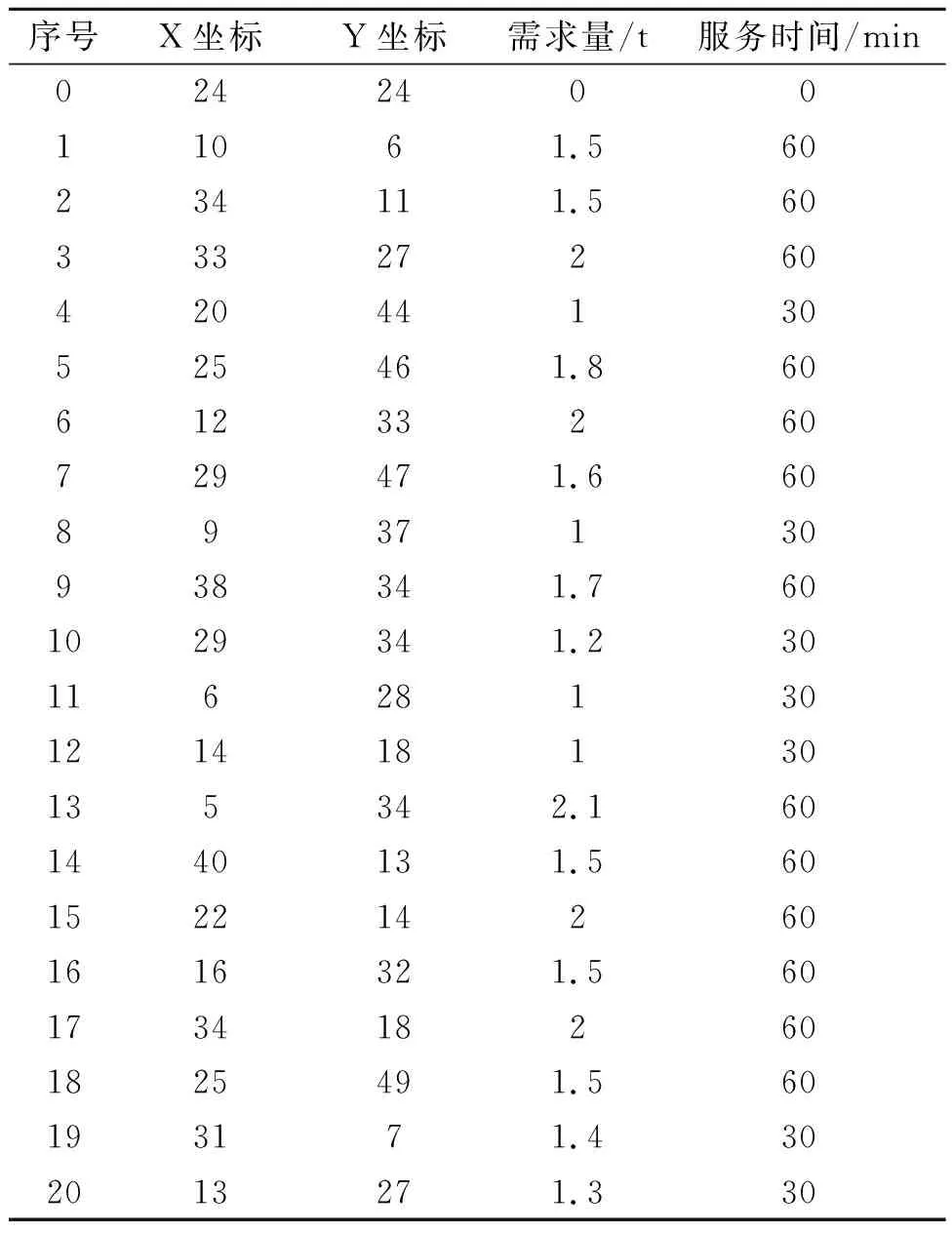
表1 客户信息表

根据上述算法和参考数据对仿真模型进行求解运算。在python程序上使用原始灰狼算法和改进灰狼算法对冷链配送模型各运行30次。两种算法的迭代图分别如图1和图2所示。迭代进化趋势表明:在开始阶段,两种算法优化速度都较快,随着迭代次数的增加,适应度的下降速度逐渐变缓。传统灰狼算法在前25代迅速迭代,在50～70代再次进一步寻优,在70代左右开始收敛,寻优结果逐渐逼近110左右,随后截止。改进灰狼算法在前25代寻优速度明显快于传统算法,而在40代左右改进灰狼算法开始收敛,寻优结果达到109左右,之后在150代跳出极值点,进一步优化,寻优结果逼近100。对比结果表明改进灰狼算法会朝着更优的方向前进,逐渐接近最优解,在取得最优解的同时避免了传统灰狼算法早熟收敛的问题。

图1 传统灰狼算法迭代图

图2 改进灰狼算法迭代图

传统灰狼算法求解结果使用6辆冷链车配送,配送路径分别为:0-4-5-18-7-0,0-17-14-2-19-0,0-12-11-6-20-0,0-3-9-10-0,0-13-8-16-0,0-15-1-0。改进灰狼算法求解结果使用6辆冷链车进行配送,配送路径分别为:0-20-11-8-13-0,0-16-6-4-0,0-5-18-7-0,0-10-9-3-0,0-17-14-2-0,0-15-19-1-12-0。最优解的配送路线如图3和图4所示。

图3 传统灰狼算法路径图

图4 改进灰狼算法路径图

对以上模型求解结果如表2所示。改进灰狼算法平均配送距离为288.49 km,最优配送距离达到284.71 km ,平均碳排放量103.24 kg,最优解碳排放量达到98.25 kg,整个过程需要6辆冷链配送车作业,每辆车配送路线如表2所示。原始灰狼算法平均配送距离为320.56 km, 最优配送距离达到312.83 km,平均碳排放量117.57 kg,最优解碳排放量达到111.21 kg,6辆配送车路线如表2所示。改进灰狼算法对于模型的求解结果总体要优于原始灰狼算法,平均配送距离上优化了10%,碳排放量减少了12.19%。综上所述,改进灰狼算法在冷链配送模型中有较好的表现,可以计算出更优配送路径,减少碳排放。

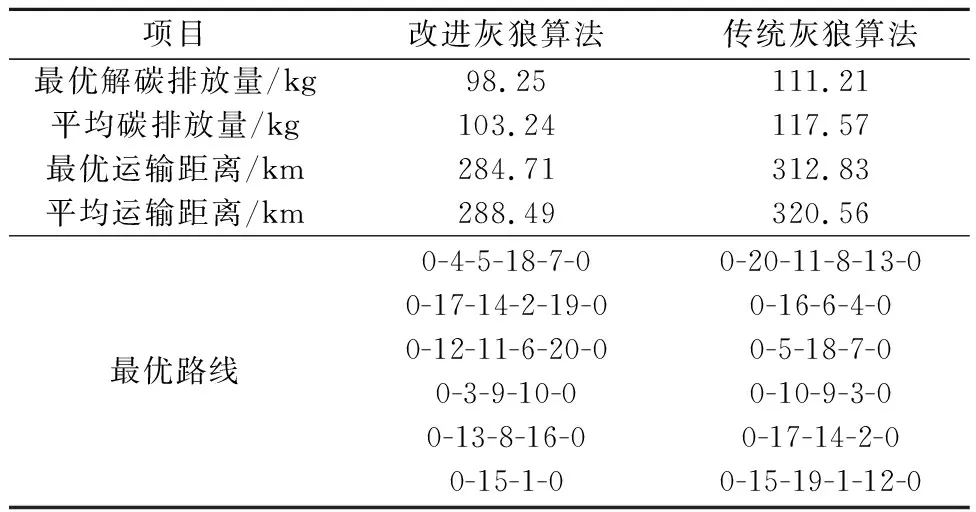
表2 算法求解结果比较

4 结论

低碳视角下促进冷链物流发展是为了更好地保护生态环境,同时也是为了满足日益增长的市场需求。在这个过程中,实现企业经济效益与生态环境效益的统一,不仅可以提高企业的竞争力,还可以为社会创造更多的价值。本文研究了基于节能减排视角下的冷链配送模型,该模型以碳排放量最小为目标,考虑满足客户需求和车辆载重等约束条件。为了进一步优化灰狼算法的优化速度并避免种群被困在局部极值区域等问题,提出了改进方法,并对仿真模拟模型进行了求解。结果表明:改进算法可以取得更优配送路径,降低碳排放量,为企业寻求发展和落实绿色物流概念提供了方法依据。