洪涝灾害下考虑需求紧迫度的应急物资配送研究——以安徽省为例

徐超毅, 刘晓絮

(安徽理工大学经济与管理学院 安徽 淮南 232001)

0 引言

近年我国洪涝灾害频发,2022年6月上中旬珠江流域暴雨洪涝灾害,6月份闽赣湘三省暴雨洪涝灾害,7月中旬四川暴雨洪涝灾害,8月上旬辽宁暴雨洪涝灾害,洪涝灾害造成巨大社会经济损失和大量人员伤亡,使人们生产生活受到严重影响。《第十四个五年规划和2035年远景目标纲要》提出要完善国家应急管理体系,提高防灾减灾抗灾救灾能力,加强核心应急救援能力建设。如何将应急物资合理快速地送往灾区是当前应急管理体系面临的重要问题。

在洪涝灾害背景下应急物流问题研究中,王付宇等[1]针对突发灾害情况下需求不确定的选址问题,构建最小化经济成本和最大化满意度的应急物资中心选址模型。对应急物资需求量进行模糊需求预测并设计改进灰狼优化算法求解问题。胡忠君[2]改进动态预测模型结合库存管理方法构建应急物资动态需求预测模型,建立目标函数为运输费用总成本最小化与救灾时间满意度最大化应急救灾物资模型。设计粒子群优化算法实现正向物流及逆向物流的应急物资分配与运输决策。贺锦等[3]运用紧迫度系数对需求满足率进行校正,解决了各求点因需求差异对公平分配造成的影响。刘欣等[4]运用层次分析法、加权综合评价法等方法,评价扬州市暴雨洪涝灾害风险水平并划分风险区域等级。王婷婷等[5]为精准预测雨灾洪涝背景下应急物资需求量,考虑灾情动态演变性并结合无偏优化和等维信息处理理论,构建改进的灾民数量动态预测方法。王伟等[6]构建城市防汛应急物资调配的多目标优化模型,采用基于Pareto概念的进化算法,用逼近理想解的排序方法得到优化结果。彭琪[7]采用间接预测的方法预测洪涝灾害下应急物资量,运用层次分析法对洪涝灾害应急物资需求紧急度的影响因素进行权重分析,以考虑配送中心运输时间周转量最小和受灾点需求满足率最大为目标,构建了多配送中心、多受灾点、多物资的大型洪涝灾害应急物资分配模型,最后利用遗传算法对模型求解。江辉仙等[8]采用动态最优路径搜索算法研究洪涝灾害约束条件下的动态优化最优转移路径,提出准动态最优路径搜索算法,计算洪涝演进过程中人员物资转移路径最优解。王泽健[9]以传统物流车辆路径问题为基础,构建了多目标的应急车辆配送路径优化模型,采用带精英策略的非支配排序遗传算法求解模型。薛书琦等[10]建立相应的心理焦虑量化函数,以最小化物流成本和心理焦虑成本为目标,构建突发洪涝灾害背景下的多周期应急物资调度模型,并通过快速非支配排序遗传算法对模型进行求解。刘明菲等[11]基于Logistic曲线建立了城市洪涝灾害应急物流能力演化模型。

为此,本文考虑在应急物资配送过程中存在受灾点对物资的需求程度和时间窗约束的情况,并且考虑到应急物资运输车辆行驶速度受天气差异影响而发生变化,拓宽了创新思路,是对现有应急物流车辆路径优化问题的进一步扩展。

1 问题描述与假设

1.1 问题描述

洪涝灾害危害性大,突发性强,很大程度上影响社会经济和人们生活。发生洪涝灾害时,合理规划应急物资运输路径,较短时间内将应急物资运往灾区,将有效促进洪涝救灾工作开展,提高救援效率。本文所研究的问题可以描述为:利用熵权-TOPSIS评价法求出洪涝灾区对应急物资的需求紧迫度,以总成本最低为目标构建考虑洪涝灾区对应急物资的需求程度约束和软时间窗约束的路径优化模型,并考虑到应急物资运输车辆行驶速度受天气差异的影响,建立晴天、雨天、阴天不同车速模型,设计混合遗传算法求解。

1.2 问题假设

为解决本文所提出的问题,特提出以下假设:(1)应急物资配送中心有着足够的应急物资和应急车辆,并且车辆类型相同;(2)应急物资配送车辆都从配送中心出发,在完成应急物资配送后,全部返回配送中心;(3)在应急物资的配送过程中,应急车辆都是保持同一个已知速度做匀速运动;(4)灾害发生时,有可能会出现道路堵塞等情况,针对应急物资配送车辆,排除此种情况,假设道路都是顺通的;(5)每个受灾点的应急物资由应急车辆配送,一辆应急车辆可以配送多个受灾点的应急物资;(6)每个受灾点的应急物资需求量是静态的,一旦确定后不会变化;(7)灾害发生时,存在一定的风险,应急配送车辆尽可能少;(8)应急物资配送过程中,只考虑车辆行驶时间,不考虑应急物资的装卸时间。

2 受灾点应急物资需求紧迫度分析

发生洪涝灾害后,为顺利开展高效紧急救援任务,不能将各个灾情点等同对待,应充分考虑受灾点对应急物资的需求程度大小。

2.1 评价指标

本文研究的是受洪涝灾害影响,相关防洪应急物资的救援配送。结合现实背景,本文采用全年降水量、水资源总量、防护林面积、常住人口、地质灾害防治投资作为评价指标。

2.2 评价方法

本文选用熵权-TOPSIS评价方法分析受灾点需求紧迫度。熵权-TOPSIS法是熵权法和TOPSIS的组合评价方法,熵权法具有客观性,能够降低因主观权重赋值所带来的误差,TOPSIS法是多目标决策分析方法。采用该方法分析受灾点需求紧迫度的思路是先用熵权法对评价指标赋权,然后用TOPSIS法分析计算各受灾点与最优解的接近度,其值便是受灾点的需求紧迫度,并进行排序[12]。

3 路径优化模型构建

本文研究的是区别于普通商业物流的应急物流车辆路径问题,以减少物资送达时间和损失最小化为最终目的。本文建立以损失最小化为目标的路径优化模型。

3.1 符号及参数变量设置

N:N={i,j|i,j=0,1,…,n}表示该区域中所有目标点的集合,其中0为配送中心,其他为受灾点;K:K={k|k=1,2,3,…,m}表示所有配送车辆的集合;k0:表示车辆的载重限制;qi:表示受灾点对于应急物资的需求量;dij:表示应急物资车辆将物资从点i配送至点j的距离;tij:车辆将物资从点i配送至点j的时间;Ti:表示应急物资配送车辆行驶至点i的时间;T0=0;Lti:表示受灾点i可以接受的最晚送达时间;φi:表示受灾点的需求紧迫度;G:表示所有使用的应急物资配送车辆的总固定成本;V:表示所用配送车辆的总行驶成本;C:表示所用配送车辆的总延误惩罚费用;S:表示所用配送车辆的总奖励费用;H:表示所用配送车辆的总成本;g:表示单个应急配送车辆的固定成本;v:表示单位距离内配送车辆的行驶成本;c:表示配送车辆的单位惩罚费用;s:表示配送车辆的单位奖励费用;xik、yijk、αi:表示0,1变量。

3.2 延误惩罚成本函数

大多数路径优化模型中会设置最早送达时间窗和最晚送达时间窗,但面对应急事件,提前将应急物资送达并不会产生等待成本,相反能够更好地体现出配送的高时效性。因此,本文仅设置最晚送达时间窗Lti,如果应急车辆将物资送到受灾点时间超过最晚送达时间,说明配送延误,产生惩罚成本。函数表达式为

(1)

3.3 行驶成本函数

将单位距离内车辆的行驶成本设为一个定值v,车辆行驶成本和行驶距离呈正相关。函数表达式为

(2)

3.4 固定成本函数

车辆的消耗费用(维修、保险、保养)和司机的工资等,这些统称为固定成本。固定成本仅与车辆数目有关,函数表达式为

(3)

3.5 奖励函数

如果车辆在受灾点的最晚送达时间之前将物资送到,给予奖励,奖励大小与需求紧迫度呈正相关。函数表达式为

(4)

3.6 总成本函数

总成本为延误惩罚费用、行驶成本、固定成本之和再扣除奖励,函数表达式为

H=C+V+G-S

(5)

3.7 目标函数

总目标函数为总成本函数。综上,考虑需求紧迫度的应急物资配送路径优化模型为

(6)

(7)

(8)

minZ=minZ1+minZ2+minZ3

(9)

约束条件为

(10)

(11)

(12)

(13)

(14)

(15)

其中:式(9)表示总目标函数;式(10)表示车辆不能超载;式(11)表示所有的受灾点都要被配送物资且一个受灾点只能由一辆车配送;式(12)表示所有车辆都从配送中心出发,在完成物资配送后返回配送中心;式(13)、(14)表示车辆将物资送到受灾点完成配送后离开受灾点;式(15)表示车辆到达受灾点j的时间。

4 求解算法

本文创建的是应急物资的配送路径优化模型,在几种常见算法中选择将遗传算法进行优化,并与模拟退火算法组合,将两种算法组合运用求解模型。

4.1 算法介绍

遗传算法从名字来看,该算法与遗传有关,它模仿的是生物学的有关理论,其实现过程和自然界生物进化相似。该算法首先进行编码,将基因型和表现型之间的相互映射关系展示出来;其次,将种群初始化;然后,对种群进行解码操作,并使用适应度函数对种群中每个个体进行适应度评判;接下来,种群根据选择函数选择优秀个体,并变异,继续产生下一代;最后留下优秀的子代。遗传算法鲁棒性好、可扩展性强、操作简单,在大规模求解组合问题上具有优势,也可用于求解多目标问题。但遗传算法需要对染色体编码进行求解并对接结果进行解码,编程相对复杂,容易早熟,陷入局部最优。

模拟退火算法模仿的是固状物质退火的一个过程。该算法首先为大环境设置初始温度和初始解,随着温度的下降,每一个温度状态下,通过解的变换生成新解。如果解的目标函数值小于前一个解,接受当前解;否则,以概率接受新解,最终的解是迭代寻优的结果。模拟退火算法从高温开始,根据温度参数慢慢降低本身温度,在降温的同时,通过概率特征跳出局部最优,在合适解集中找出全局最优解。该算法运行效率高,但是收敛速度较慢,计算执行时间较长,对参数设置相对敏感。两种算法对比如表1所示。

表1 算法对比

4.2 算法设计

(1)基本算法流程

首先,结合模型的特点设计组合算法的相关参数值大小,按照一定的编码规则构造初始种群。其次,开始种群的迭代:(1)考虑种群的适应度,本模型的适应度取值为总目标函数的倒数;(2)完成遗传算法的选择、OX交叉、变异、重新插入等运算;(3)进入模拟退火,把经过邻域结构后生成的新解与当前解加以对比,若新解好,则新解替换当前解,同样总成本也按新解计算,若新解不好,根据退火准则,得到同意更换新解为当前解的概率p,此时随机生成一个[0,1]区间的数,若该数比p小,那么同上将更换新解为当前解,并更新当前解的成本;(4)将全局最优解与当前解进行比较,若全局最优解没有当前解效果好,则当前解取代全局最优解,同时更新全局最优解总成本。最后,根据上述迭代过程,算法持续循环,当种群迭代到算法初始设置的迭代次数时,结束循环,输出最优解。

(2)关键参数设置

算法中关键参数的设置如表2所示。

表2 参数设置

5 实证分析

本文选取安徽省作为研究对象。研究当安徽省遇到洪涝灾害时,应急车队如何合理高效地配送物资。

5.1 受灾点需求紧迫度算例分析

5.1.1 数据准备

通过查找2022安徽省统计年鉴,获取了安徽省16个市有关数据(如表3所示)。

表3 受灾点具体数据

续表3 受灾点具体数据

5.1.2 过程及结果分析

通过熵权法,首先计算这5个评价指标的权重,然后根据权重对数据进行二次加权(如表4所示)。

表4 熵权法计算权重结果

再对上述重新生成的数据进行TOPSIS分析:对常住人口、全年降水量、水资源总量、防护林面积和地质灾害防治投资这5个指标进行TOPSIS评价,评价对象为安徽省的16个市,该评价结果的接近程度值便是本文各受灾点的需求紧迫度。最后对其进行排序,得到安徽省16个市的需求紧迫度排序结果(如表5所示)。

5.2 路径优化算例分析

5.2.1 数据准备

配送中心与需求点:本算例的配送中心选择位于合肥市瑶海工业园区的百大物流园,此物流园位于新海大道(物流大道)与当涂北路交叉口,占地面积100亩,总建筑面积47000 m2。需求点为安徽省的16个市,配送中心编号为0,16个区的编号分别为1至16。

物资需求量:本算例的应急物资为医疗药品,物资需求量根据每个地区的常住人口进行计算,具体数据由表3可知,假设一个人需要1 g的医疗药品,计算得出每个受灾点的物资需求量(见表6)。

表6 受灾点具体数据

最晚送达时时间:需求紧迫度与最晚送达时间呈反比例关系,规定需求紧迫度最小的受灾点最晚送达时间为2,公差为0.04,按照等差数列依次设置最晚送达时间(见表6)。

车辆行驶速度:此次应急运输车辆为中卡货车,考虑车辆行驶速度会在一定程度上受天气影响,卡车在不同天气下有不同的速度。参考朱凯家[13]的速度模型,得到运输车辆在晴天、中雨天、小雨天和阴天的平均行驶速度(见表7)。

表7 车辆行驶速度

需求点之间的距离:根据地图,在道路通畅的情况下,得到配送中心和每个受灾点的距离。

在此模型中还有一些其他数据,具体数据如表8所示。

表8 其他相关数据

5.2.2 结果分析

按照上述数据和参数,基于Matlab R2021b平台,对此模型进行仿真求解,得到在4种不同天气下考虑需求紧迫度的洪涝灾害路径优化结果如表9、图1至图4所示。然后将模型中各受灾点需求紧迫度设为0,得到在4种不同天气下不考虑需求紧迫度的洪涝灾害路径优化结果如表10、图5至图8所示。将考虑受灾点需求紧迫度和不考虑需求紧迫度的模型进行对比。

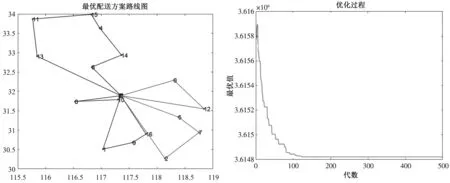
图1 晴天考虑需求紧迫度车辆配送路径

图2 小雨天考虑需求紧迫度车辆配送路径

图3 中雨天考虑需求紧迫度车辆配送路径

图4 阴天考虑需求紧迫度车辆配送路径

图5 晴天不考虑需求紧迫度车辆配送路径

图6 小雨天不考虑需求紧迫度车辆配送路径

图7 中雨天不考虑需求紧迫度车辆配送路径

图8 阴天不考虑需求紧迫度车辆配送路径

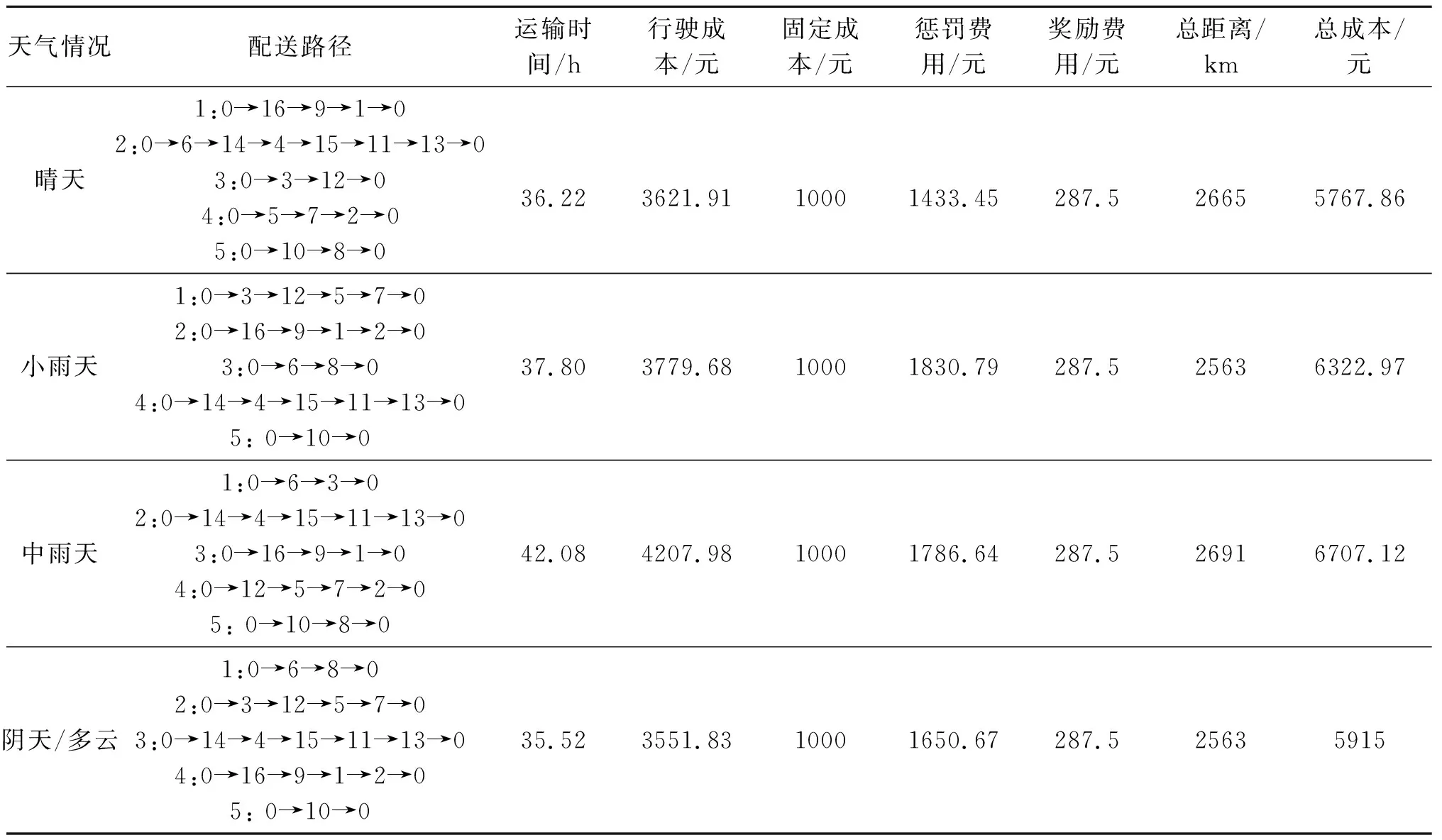
表9 考虑需求紧迫度结果

表10 不考虑需求紧迫度结果

由图1至图8及表9、表10可知,(1)考虑需求紧迫度和不考虑需求紧迫度的路径优化模型最优解均使用了5辆车,两模型的固定成本相同;(2)考虑需求紧迫度模型中的4种不同天气下的最优配送车辆路径总成本和配送时间均要低于不考虑需求紧迫模型。其中,晴天时考虑需求紧迫度模型的总成本比不考虑需求紧迫度模型的总成本减少了5.86%;小雨天考虑需求紧迫度模型的总成本比不考虑需求紧迫度模型的总成本减少了4.55%;中雨天考虑需求紧迫度模型的总成本比不考虑需求紧迫度模型的总成本减少了4.29%;阴天考虑需求紧迫度模型的总成本比不考虑需求紧迫度模型的总成本减少了4.43%;(3)图1至图8中可以看出,迭代开始阶段,两种模型直线大幅度快速下降,说明算法优化速度快,但随着迭代次数的增加,线性变化逐渐趋于平缓,考虑需求紧迫度模型较早找到最优值。混合算法可以在保证收敛速度较快的前提下,较好地实现搜索全局最优的目标,能够弥补两种算法本身的不足,验证了模型的有效性。

6 结论

本文在洪涝灾害背景下针对应急物流的路径优化问题进行了研究,以安徽省为算例背景:

(1)建立受灾点对物资的需求紧迫度评价体系,采用熵权-TOPSIS法分析得出了受灾点的需求紧迫度。

(2)研究基于软时间窗下的应急物流路径优化问题,建立了以损失最小化为目标的路径模型,将需求紧迫度引入模型,并考虑运输车辆的行驶速度会受天气影响而发生变化,针对模型特点设计并改进混合遗传算法进行求解。

(3)结合实例进行仿真试验,结果表明,本文设计的算法在求解面对洪涝灾害应急物流路径优化问题时比传统未改进算法更具有明显优势,缩短物资运输时间,减少损失,有较好的稳定性,能够相对有效解决应急物流路径优化问题。

(4)注重灾区实际需求,引入受灾点需求紧迫度,根据实际情况考虑车辆行驶速度受天气影响,大力提高应急工作救援效率。

(5)着重体现应急管理部门在突发灾害时对应急物资配送的时效性、经济性和公平性要求,为应急部门提供具有一定参考价值的决策方案,为大型洪涝灾害后的应急救援行动提供一定帮助。