基于数字化技术的甲供材合理超供方案设计
——以南京地铁项目为例
周明月 李蕾蕾 苏诗玮 李洁(.南京地铁建设有限责任公司,江苏 南京 007;.南京林业大学土木工程学院,江苏 南京 0037)
0 引言
在地铁工程项目建设过程中,涉及的材料、设备种类繁多。业主方为了保证全线路的质量和装修风格统一,通常对防水材料(如防水卷材)、装饰材料(如外墙砖)及内置固定构件(如盾构管片)等采用甲供模式。但是,在实际项目建设中,甲供材的用量大、不确定因素多,其数量往往难以确定。因此,在甲供材使用过程中,经常出现甲供材超供现象,即材料实际使用量超过经计算的理论用量。
通常情况下,人们直观认为甲供材超供是由承包商造成,如材料浪费、利用甲供材价格优势赚取差价、擅自更改甲供材范围超领材料等[1]。上述现象虽然存在,但是,项目复杂多变的特点使得甲供材超供存在一定的合理性,如甲供材计划不准确、工程变更不及时申报、业主需求变化等。本文将这种非承包商恶意原因,由不确定因素引起的超供现象称为合理超供。
现阶段,甲供材超供往往采取“一刀切”的管理方法,忽视了甲供材合理超供的需求,导致管理混乱,阻碍了工程的顺利进行。因此,科学的甲供材预测对避免甲供材超供十分重要。目前,已有部分学者研究了甲供材合理超供影响因素。王永胜[2]提出,设计变更、供应范围调整等造成的甲供材超供现象是合理的,需要对甲供材合同清单数量进行动态调整,但未深入研究如何有效解决甲供材合理超供问题。傅道友[3]指出,工程设计变更会导致甲供材供货与现场实际需求不匹配,提出建立甲供大宗材料数据平台,实现设计变更数据反馈,进行甲供材增补。但是,该做法属于滞后补偿,未能从本质上解决甲供材合理超供管控问题。
为了制订合理的甲供材供应计划,本文通过文献研究与调查法识别甲供材合理超供的主要影响因素,设计甲供材合理超供方案,建立经粒子群算法优化的最小二乘支持向量机预测模型,以获取甲供材合理超供范围,从而实现地铁项目甲供材合理超供的范围管控。
1 研究方法概述
1.1 最小二乘支持向量机
支持向量机(Support Vector Machines,SVM)是Vapnik等根据统计学理论提出的一种新型学习算法[7],而最小二乘支持向量机(LSSVM)作为标准SVM的一种扩展与改进算法,具有算法简单、稳定性强、准确性高等优点。对于解决甲供材合理超供的多因素、非线性、不确定性等问题具有明显优势,且不受样本容量限制。为保证LSSVM模型的参数最优、预测精度更高,本文采用粒子群(Particle Swarm Optimization,PSO)算法优化的最小二乘支持向量机(PSO-LSSVM)作为甲供材合理超供预测工具。
假设训练样本集D={(xi,yi),i=1,2,…,n},xi∈Rd,yi∈Rd。其中,xi为输入向量,yi为输出向量。LSSVM的核心思想为使用非线性映射φ(xi)将输入集Rd映射到高维特征空间,构造出最优线性回归函数,公式如下
f(x)=ω×φ(x)+b
(1)
式中,ω和b分别表示回归函数的权值向量和偏差量。根据结构风险最小化原则,确定ω值和b值。同时,建立Lagrange函数用于调节经验风险和模型复杂度之间的关系,求得参数,得到LSSVM预测模型,公式如下
(2)
式中,K(x,xi)为核函数;α为Lagrange乘子。利用最小二乘法求解得到α和b。
1.2 粒子群算法
LSSVM模型通常采用交叉验证法对其参数进行寻优,但效率低、精准性不高[8]。因此,结合粒子群算法进行优化参数设置,以优化预测结果。粒子群是一种利用个体之间的协作实现整个群体从无序到有序的演化运动过程,是寻求最优解的一种全局最优化算法[9]。在PSO算法中,由m个粒子组成的群体对d维空间进行搜索,粒子位置和速度分别表示为xi=(xi1,xi2,…,xid),vi=(vi1,vi2,…,vid),粒子寻优方式如下
(3)
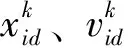
2 地铁项目甲供材合理超供影响因素分析
2.1 影响因素识别
目前,甲供材用量一般通过套取定额计算获得,其定额不仅包含净用量,还包含材料损耗量。但是,定额中规定的材料损耗量是按照国家建筑行业平均水平确定的,随着项目、技术复杂性的提高,难以完全涵盖实际地铁项目中的损耗量,这也成为甲供材合理超供现象的主要原因之一。此外,定额计算中仅考虑的工艺性损耗因素无法完全满足全面的甲供材合理超供需求,如管理不善导致的非工艺性损耗等因素也是甲供材合理超供的原因之一。
为了获取影响甲供材合理超供的主要指标,本文通过文献梳理与调查法,归纳得出各方主体影响甲供材超供的因素。从合理超供概念出发,与主体责任承担相结合,作为甲供材超供合理性判定的标准,筛选出甲供材合理超供影响因素。判定标准包括:不属于非承包商引起的恶意超耗;由各方主体甲供过程的不确定性引起;归属于各方主体的承担责任,而非个人责任;合理超供因素之间无重叠性。
2.2 影响因素确定
采用问卷调查法邀请相关专家根据自身经验对各指标进行打分。调查问卷主要由两部分组成,第一部分涵盖被调查者的专业背景信息及经验,第二部分主要通过李克特5级量表对甲供材合理超供影响因素进行评估,数值越大,代表指标影响越大。共收到来自业主、承包商、造价单位、监理单位的23名专家的有效反馈,确定4个甲供材合理超供重要影响因素(分值超过3分),分别为材料损耗计取、工程变更、施工操作损耗和施工管理水平。为了将甲供材合理超供按照不同种材料进行区别,增加材料类别,最终确定5个甲供材合理超供影响因素,见表1。
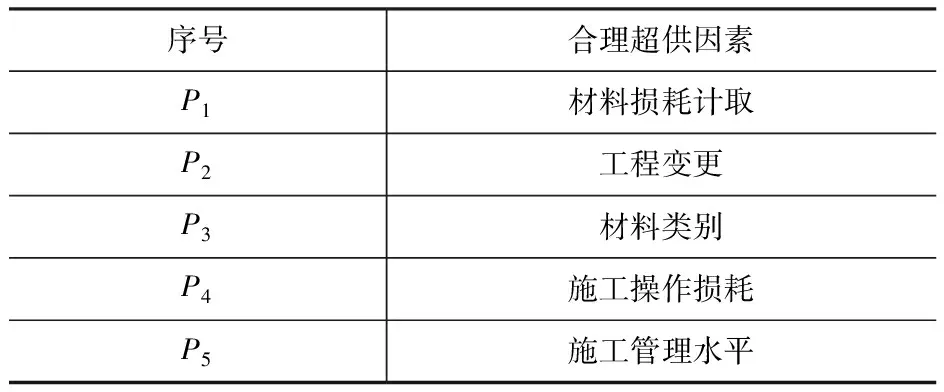
表1 甲供材合理超供影响因素
3 基于PSO-LSSVM的甲供材合理超供预测模型
3.1 模型适配性
甲供材合理超供受多种因素影响,具有非线性特征。因此,甲供材合理超供预测的实质是分析甲供材合理超供与其影响因素之间的统计关系,属于被解释变量与多个解释变量的非线性回归问题,难以通过一般的数学方法统计分析。而PSO-LSSVM预测模型的核心思想是使用核函数将输入变量映射到高维特征空间,将非线性问题转换为最优线性回归问题,并由核函数与参数相结合的预测模型输出预测量。因此,该模型适用于甲供材合理超供分析预测过程,具有极高的适配性。
基于PSO-LSSVM甲供材合理超供预测模型,在一定样本数据训练下,将合理超供影响因素作为模型的输入指标,将实际供应量作为已知输出变量,经过参数优化的核函数映射后,分析各影响因素与合理超供量之间的关系,输出合理超供预测值。基于PSO-LSSVM的甲供材合理超供预测模型示意图如图1所示。
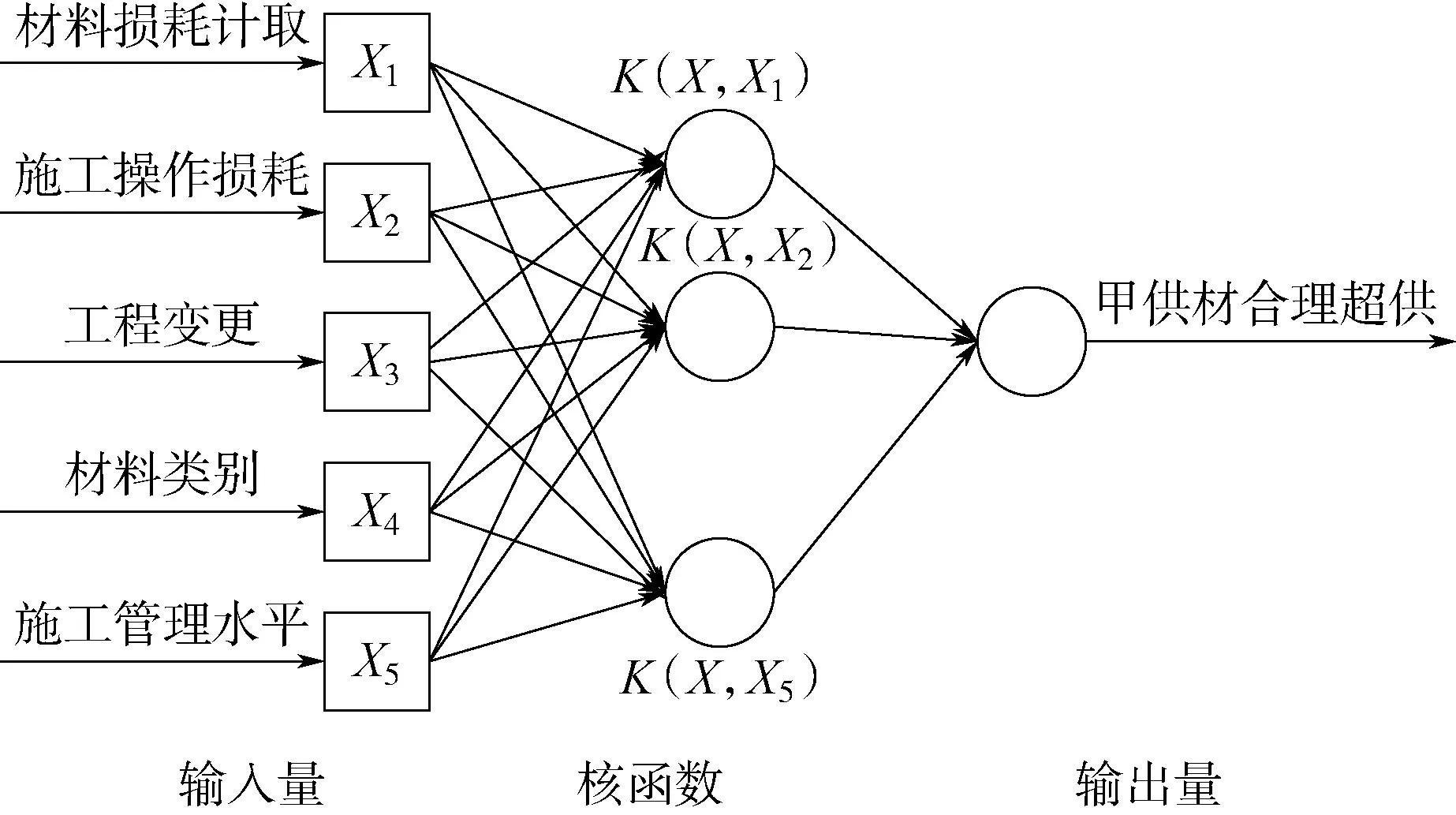
图1 基于PSO-LSSVM的甲供材合理超供预测模型示意图
3.2 模型构建与优化
3.2.1 建立预测模型
不同的核函数会形成不同的预测模型,LSSVM常用的核函数有径向基核函数、多项式函数、线性函数等[10]。径向基核函数具有较强的泛化能力,训练误差和检验误差较小。因此,本文将其作为核函数,建立基于PSO-LSSVM的甲供材合理超供预测模型。公式如下
(4)
式中,α和b分别为最小二乘法求解得到的乘子和偏差量;xi为输入向量;σ为核参数,其值过小容易欠拟合,过大则容易过拟合[11]。
3.2.2 构建合理区间
为了获取更加准确的甲供材合理超供预测区间,基于区间估计原理,在点估计的基础上加减标准误差,给出总体参数估计的区间范围,将个体预测转化为区间预测。

3.3 样本数据的规范化处理
首先,对定性指标进行量化。工程变更指标的量化采用无量纲处理:有工程变更为1,无工程变更为2。材料类别的量化方法为:防水材料为1,装修材料为2,内置固定构件和外置槽道为3。施工管理水平的量化按照优、良、中、差4个级别分别量化为1、2、3、4。甲供材合理超供预测指标取值见表2。
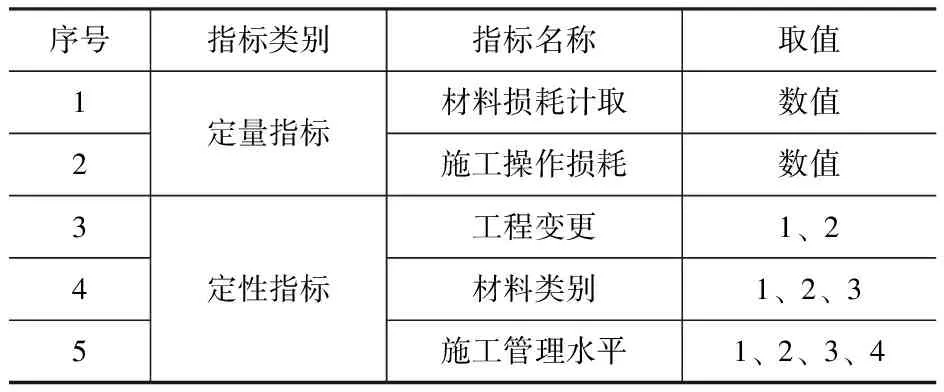
表2 甲供材合理超供预测指标取值
为消除量纲对数据分析的影响,提高输入与输出数据的精度与收敛性,对样本数据进行归一化处理。归一化公式为
(5)
式中,x、xi分别为归一化处理后和归一化处理前的值;xmax、xmin分别为所属预测指标下的最大值和最小值,进行归一化后的数据压缩至[0,1]。
3.4 参数优化及预测流程
为使误差保持在最小范围内,参数应通过训练样本集进行训练优化选取。PSO算法能快速对参数进行全局寻优。基于PSO-LSSVM的甲供材合理超供数量预测流程图如图2所示。
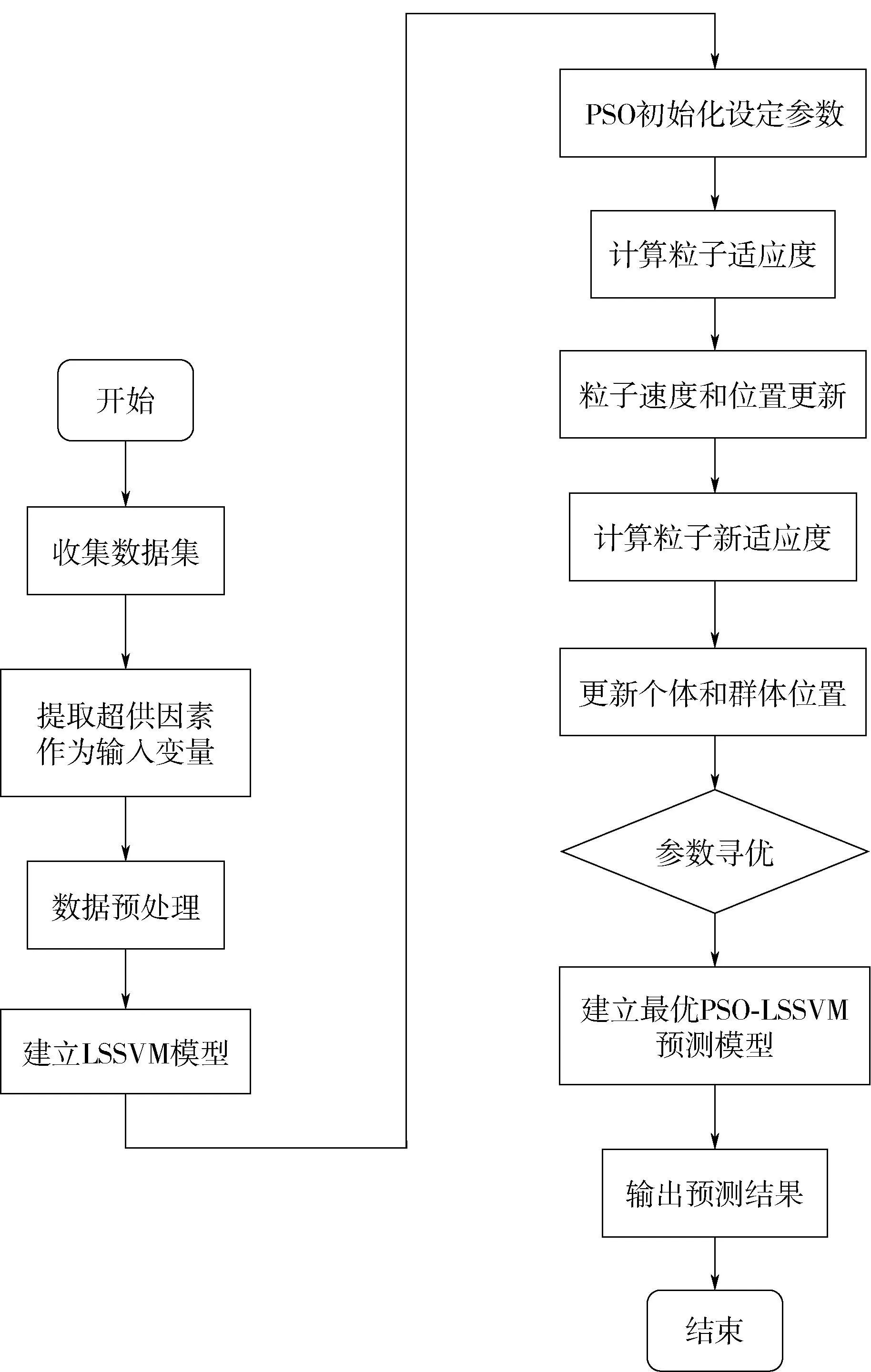
图2 基于PSO-LSSVM甲供材合理超供数量预测流程图
4 案例分析
4.1 数据样本选择
选取南京地铁1号线北延工程、南京地铁2号线西延工程、南京S8线南延工程三个项目的甲供材超供数据信息,包含防水材料、装修材料、内置固定构件和外置槽道三大类,共129条样本数据,涉及数十家承包单位。搜集并整理材料损耗计取、施工操作损耗、工程变更、材料类别、施工管理水平5项指标数据,及各项甲供材实际供应数量(Y)作为甲供材合理超供数量预测的样本数据,见表3。

表3 南京地铁建设项目甲供材样本数据
4.2 预测模型训练与检验
为验证PSO-LSSVM模型进行甲供材合理超供数量预测的有效性和准确性,采用Matlab软件将其与LSSVM模型的预测结果进行对比。在两种模型预测过程中,共选取129组数据作为数据样本,训练样本与测试样本之比设置为0.9。步骤如下:
(1)LSSVM预测模型将参数C和σ初始设置为1,采用交叉验证法在训练集中对参数寻优,输出预测结果。
(2)PSO-LSSVM预测模型在LSSVM预测模型的基础上增加PSO优化算法,其参数初始化设置见表4。
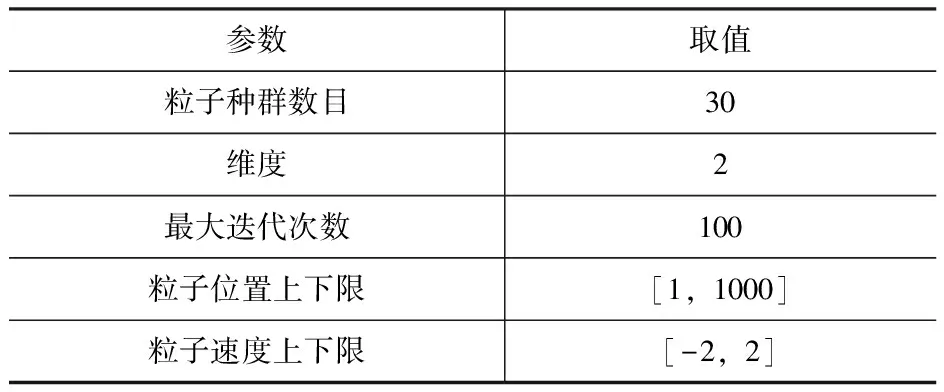
表4 PSO-LSSVM预测模型参数初始化设置
(3)为对两种预测模型的精确度进行直观评价,通常采用均方根误差(RMSE)与决定系数(R2)进行分析。RMSE越小,预测精度越高;R2越接近1,拟合效果越好。计算公式如下
(6)
(7)
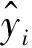
4.3 预测对比分析
采用LSSVM和PSO-LSSVM两种预测模型分别对南京地铁建设项目甲供材相关数据进行仿真预测,两种预测结果对比如图3和图4所示。

图3 基于LSSVM的甲供材合理超供数量训练集预测结果对比

图4 基于PSO-LSSVM的甲供材合理超供数量测试集预测结果对比
通过上述公式,计算得到基于两种模型的南京地铁建设项目甲供材合理超供预测数量评价结果,结果对比见表5。
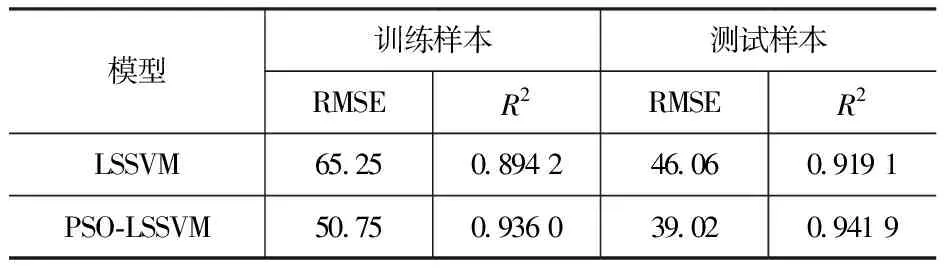
表5 基于LSSVM和PSO-LSSVM的甲供材合理超供数量预测结果对比
从两种预测模型的误差计算可知,相比LSSVM预测模型,PSO-LSSVM预测模型的RMSE更小,仅为39,且R2更接近1,说明PSO-LSSVM预测模型的预测性能更优。
4.4 预测区间分析

以装修材料样本数据之一的某LED双头格栅筒灯数据为例,其基于PSO-LSSVM的甲供材合理超供预测模型的输出预测值为517.158,因此,合理超供区间为[440.68,593.64]。此样本实际值为458,处于预测超供数量区间内,验证了该预测模型的有效性。由此可见,基于PSO-LSSVM的甲供材合理超供预测模型为甲供材合理超供控制提供了新方法。
5 结语
针对地铁项目甲供材合理超供现象难以管控的问题,本文设计了基于数字化技术的甲供材合理超供方案,即在影响因素分析的基础上建立一种基于PSO-LSSVM的甲供材合理超供预测模型,并应用于南京地铁建设项目进行实验验证。主要结论如下:
(1)通过调查法获取地铁项目中甲供材合理超供的重要影响因素,并以此构建预测指标,提高预测模型在实际应用中的指导意义和实践价值。
(2)PSO算法优化了LSSVM预测模型中的参数,降低了预测误差,在整体上与原数据拟合程度高,具有较高的有效性和可行性。
(3)本文的预测实验研究存在一些不足之处,部分相关问题仍需要进一步分析和验证。如针对材料类别这一预测指标,可以根据不同材料型号和规格进行细化,以提升实验的精确性。

