基于HMM 的逆雷达辐射源状态识别推理方法

朱梦韬，张露瑶，李瑞，杨静

（1.北京理工大学 信息与电子学院, 北京 100081；2.电子信息系统复杂电磁环境效应国家重点实验室, 河南, 洛阳471003；3.电磁空间认知与智能控制技术实验室, 北京 100191）

近年来，随着人工智能等先进技术在雷达对抗场景中的雷达方和干扰方系统中获得越来越多应用，对抗双方系统的精准对抗博弈能力不断提升.通过引入机器学习类算法模型，干扰方可以对多功能雷达（multi-function radar, MFR）的工作状态以及动态特性实现快速准确识别与估计，用以支撑后续干扰效果评估和自适应干扰决策[1].典型研究如基于观测雷达状态序列构建反映雷达各层次行为特征的状态识别模型，如隐马尔可夫模型（hidden Markov models，HMM），深度学习模型等，实现对雷达行为意图的识别与动态特性估计[2-11]；雷达方则往往基于机器学习框架构建各类神经网络模型实现对复杂干扰信号的高效精准识别，从而有效提高抗干扰性能[12-18].对抗双方系统都亟须寻求根据所掌握先验信息及部分可观测结果获取更丰富和更准确的对手系统信息的技术手段，以便在对抗博弈过程中取得优势.因此，针对无法直接观测得到的对手系统内部细节信息（如干扰方状态识别的性能）进行逆向推理技术研究开始进入研究者的视线.

针对对手系统的逆向推理研究是一个逐步扩展深入的过程.最初是根据给定的系统结构及决策（控制）策略逆向分析出反映系统动作的最优性能指标值[19].随后研究者开始关注从对手系统外在动作层面对其内部系统信号处理环节状态进行推理，有研究假设在对抗场景中的我方状态转移概率模型及给定对方策略下的我方观测到动作概率模型、对方观测似然概率模型均已知，并据此假设通过已知的我方系统信息及可观测的对方系统信息逆向分析得到对方对我方的估计结果[20].同样基于上述概率模型均已知的假设条件下，最近扩展到了更深层次的控制策略（目标函数）[21]的逆向推理，即针对对方系统中效用函数进行逆向分析的研究.李瑞等[22]构建了雷达对抗场景中的逆向推理总体框架，并展现了涵盖双方系统各级功能模块的逆向分析交互过程.

针对自主系统的逆向推理实现方法研究方面，KRISHNAMURTHY 等[20]学者将具有认知能力的无人机或雷达系统作为对手，提出利用逆滤波方法估计对方系统在观测条件下对我方系统状态的后验分布，并根据估计结果设计了有效对抗自主系统的反自主系统.MATTILA 等[23]基于构建的隐马尔可夫模型结合贝叶斯滤波器输出的后验分布序列，采用逆滤波方法逆向推理出对方传感器精度及所观测序列.文献[24 - 26]引入在针对智能体行为（策略）逆向推理中广泛应用的逆强化学习技术，利用所观测到的智能体行为轨迹或决策策略逆向分析智能体效用函数.KRISHNAMURTHY 等[27]从干扰方角度结合显示偏好理论证明了利用逆滤波方法能够估计雷达方的估计结果和传感器精度以达到有效逆跟踪的目的.

综上所述，逆向推理技术具有在非合作条件下分析发觉对手系统内部更多有效信息的潜力，但已有研究[20]需假设非合作系统内部的各个处理环节已知，从而逆向推理技术转变为根据观测对非合作系统中变量节点的后验计算问题.本文从提升雷达系统抗干扰能力出发，考虑干扰方具备根据观测得到的雷达信号序列进行雷达工作状态识别及预测，并基于识别预测结果调整其干扰动作的能力.由于非合作系统内部处理环节[20]实际对我方未知，本文将考虑通过构建隐变量的方式，从可观测雷达和非合作方交互序列入手，设计了对干扰系统对我方雷达辐射源状态识别结果的逆向估计方法，从而获取干扰方状态识别模块对我方雷达状态识别的准确度.该逆向分析结果也可用于辅助对未来时刻干扰方动作的预测等后续任务.雷达对抗仿真实验结果验证了所提方法的可行性和准确性.

1 雷达对抗场景中的逆状态识别模型

本文结合文献[22]中构建的雷达对抗场景下的逆向推理框架，以及文献[2 - 11]中干扰方基于观测雷达信号序列对雷达工作状态进行识别的研究成果，从雷达方视角对逆信号处理模块中逆辐射源状态识别问题进行建模与求解.基于MFR 前后工作状态间高度相关性使得干扰方对雷达工作状态识别的结果序列前后状态间也具有潜在相关性的时序特性，雷达方可将干扰方用来控制干扰发射信号的干扰方对雷达方真实状态的识别结果变量视为服从马尔可夫过程的隐变量，将雷达方对干扰方通过工作状态识别后采取的干扰样式输出动作的识别结果作为雷达方可观测变量.由此雷达可构建干扰系统内部的“雷达状态识别结果（隐藏层）-雷达观测干扰动作（观测层）”的HMM 模型.具体的，雷达方对干扰方辐射源状态识别环节逆向推理任务图如图1 所示.

图1 雷达方对干扰方辐射源状态识别逆向推理任务图Fig.1 Flow chart of inverse inference for radar to recognize the jammer emitter work mode

上述干扰方和雷达方之间的交互过程的概率模型如下：

式中：k=1,2,···,N表示离散化时间；p(·)表示条件概率密度函数或条件概率质量函数； ～表示服从的分布.其中k时刻MFR 信号对应的真实工作状态为qk，在干扰方视角通常假定qk的转移具有一阶马尔可夫性.干扰方基于观测信号yk完成对k时刻MFR 的真实工作状态的识别，为识别结果.由干扰方的状态识别模型决定，为服从某种概率分布的算子,该概率密度分布对应了状态识别模型的混淆矩阵性质.例如在现有典型干扰方研究中[2-11]，干扰方状态识别模型输入雷达脉冲序列，输出识别得到的雷达工作状态概率分布，此时.为描述简便，本文建模时不考虑干扰方机动对我方雷达状态切换的影响,该假设对本文提出的方法没有影响.

本文设计的逆状态识别过程不需要P,E,G的先验知识，通过对离散的和构建离散隐变量状态空间HMM 模型，利用隐变量和状态转移矩阵、观测矩阵分别表征交互过程中的中间变量和条件概率分布，凭借观测数据学习参数P,E,G,具体如下：

设定n为时间序列长度，雷达通过对干扰方实施的真实干扰样式动作序列U={u1,u2,···,un}进行干扰样式识别后得到的动作观测序列O={o1,o2,···,on}估计干扰方对雷达真实工作状态序列Q={q1,q2,···,qn}的识别结果，得到逆状态识别序列

针对上述逆状态识别问题，构建雷达方基于HMM的逆辐射源状态识别模型，该HMM 记为λ={A,B,π}，其中：

（2）雷达方所观测到的干扰样式数目为M，干扰样式集合记为V={V1,V2,···,VM}.

（3）干扰方状态识别模型中的状态转移概率矩阵为A=[aij]，其中aij=,i,j=1,2,···,N，用于描述干扰方对MFR 工作状态识别模型中估计得到的各雷达状态间的转移概率.

（4）观测特征概率分布矩阵为B=[bij],bij=P(ok==Si),i=1,2,···,N,j=1,2,···,M，用于在干扰方状态识别结果条件下雷达观测到干扰样式ok的概率.

（5）初始状态概率分布为π=[πi] ,πi=,i=1,2,···,N表示初始时刻干扰方状态识别结果的概率分布.

此外，记真实MFR 工作状态集合为D={D1,D2,···,DN}，雷达采取的抗干扰措施序列为Z={z1,z2,···,zn}，其中z∈W，W={W1,W2,···,WL}为雷达抗干扰措施集合，L为抗干扰措施总数.

2 HMM 模型下的逆状态识别推理算法

本节基于上述逆辐射源状态识别HMM 模型，设计对应的模型参数初始化和模型训练方法，以及基于该模型的逆状态识别任务求解方法.首先运用自适应粒子群优化（adaptive particle swarm optimization,APSO）算法获取HMM 模型的初始参数λ0={A0,B0,π0}.然后通过多观测序列的Baum-Welch 算法训练得到最优参数λ*={A*,B*,π*}，使得HMM 模型在该给定参数 λ*的条件下，出现观测干扰样式序列O的概率P(O|λ*)最大.最后利用对数Viterbi 算法解决雷达方在已知模型最优参数 λ*和观测干扰序列O的情况下，得到可解释该观测干扰序列O的干扰方识别结果的逆状态识别序列

2.1 基于自适应粒子群算法的HMM 参数初始化

HMM 模型的初始参数λ0={A0,B0,π0}会直接影响模型的训练结果.其中A0和 π0对模型训练结果影响较小，可采用均匀分布或平均分布取值[28].对B0，本文采用自适应粒子群优化（APSO）算法进行参数初始化.

为解决带有等式约束的HMM 初始参数优化问题，本文采用罚函数法[29]，增加惩罚项后适应度函数表示为

式中：函数f(x)即由前向-后向算法所得的P(O|λ) ，σ为惩罚因子；P(x)为整体惩罚项.

为计算P(x)将等式约束条件转换为不等式约束，有

其中， ε为等式约束容忍度值.

整体惩罚项P(x)为

式中：Lk表示每个约束惩罚项的权重；ek(x)=max(0,|gk(x)|-ε).

2.2 基于多观测序列HMM 参数优化的逆状态识别

2.2.1 多观测序列的HMM 参数优化

考虑截获到多条独立同分布的观测干扰样式序列，记为O′={O(1),O(2),···,O(K)}，其中K为观测序列总数.本节基于多观测序列Baum-Welch 算法和初始化后的HMM 参数λ0={A0,B0,π0}进行模型参数的优化训练，具体如下：

记第k个观测序列为O(k)=，其长度为nk.模型训练的目标函数为

其中，将已知参数λ={A,B,π}时第k个干扰样式观测序列出现的概率P(O(k)|λ)记为Pk.将不同观测序列频率累加可得修正后的重估公式[30]为

2.2.2 基于对数Viterbi 算法的隐状态估计

雷达方对干扰方辐射源状态识别环节的逆向推理是状态估计问题，因此在训练观测序列O′={O(1),O(2),···,O(K)}上进行参数估计获得最佳模型 λ*后，针对测试观测序列需要估计出对应的干扰方辐射源状态识别结果序列.本文采用对数Viterbi 算法避免由于输入的观测序列较长，计算所得概率过小导致的数值下溢问题[31].

针对单观测序列O={o1,o2,···,on}，定义变量χt(i)为式(12)，表示在已知HMM 参数λ={A,B,π}的条件下，到t时刻为止观测序列为O={o1,o2,···,ot}情况下，出现概率最大的系统隐状态序列，且=Si.

χt+1(i)可通过式(13)迭代得到.

3 仿真验证

3.1 仿真场景设置

本文所用仿真场景如图2 所示，雷达方为地基多功能相控阵雷达，干扰系统包括远距支援和自卫干扰两部分，可在对多功能雷达状态进行识别后进行干扰决策，执行相应干扰样式.

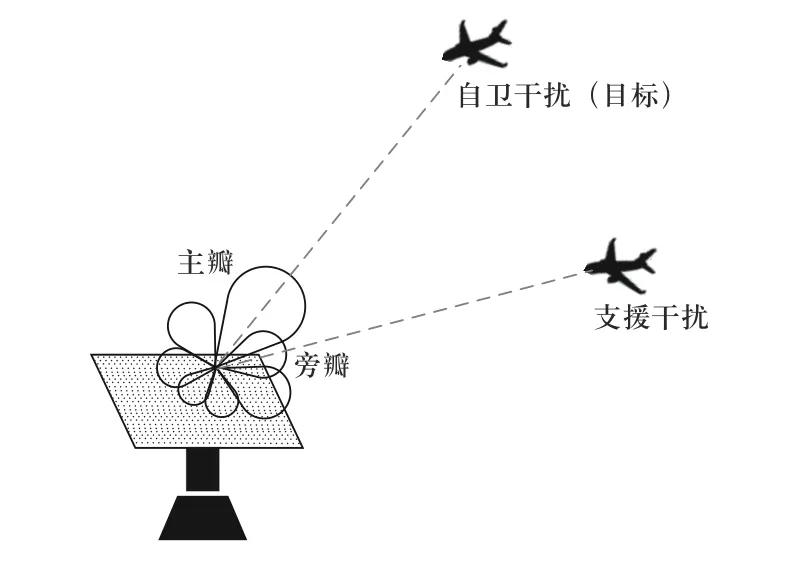
图2 “空对地”干扰场景示意图Fig.2 Diagram of "air-to-ground" jamming scenario

设置仿真场景中，干扰方有3 种干扰措施分别为密集假目标、噪声压制和拖引干扰；雷达方的4 种工作状态为搜索、确认、跟踪和识别；雷达方可采取的4 种抗干扰措施为无抗干扰措施、频率捷变、旁瓣匿影和记忆波门跟踪.对应地，逆状态识别HMM模型中的干扰样式个数M=3，隐状态个数N=4，抗干扰措施集数L=4.表1 为专家经验指导下的雷达双方干扰与抗干扰措施设置.

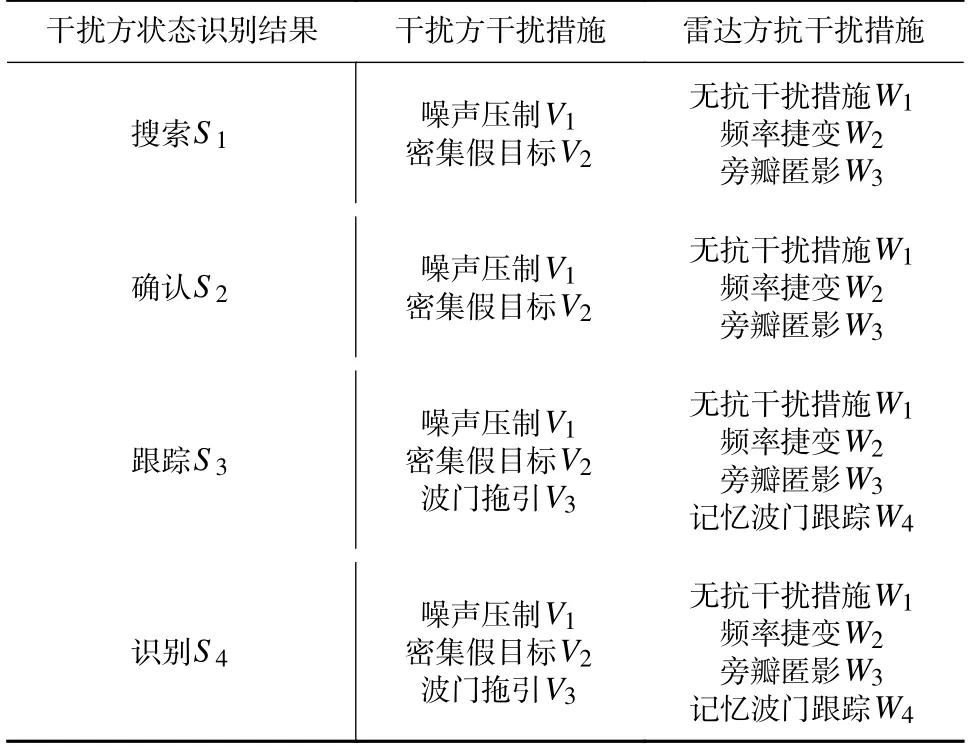
表1 雷达对抗双方的干扰与抗干扰措施设置Tab.1 Jamming and anti-jamming measures setting for both sides of radar countermeasure

3.2 仿真数据生成

本文依照第1 节中的交互模型基本思想，设计采用如图3 所示流程产生仿真所需真实雷达状态序列Q、干扰方对MFR 工作状态识别结果序列、干扰方真实干扰样式序列U及雷达方观测干扰样式序列O，用于模型训练与测试.

图3 仿真序列生成关系示意图Fig.3 Diagram of simulation sequence generation

为了简便，本文假设观测干扰样式序列O与干扰方真实干扰样式序列U相同.

3.2.1 真实观测特征概率分布矩阵生成方法

本节介绍真实观测特征概率分布矩阵Br=[bri j]N×M的仿真方法，即brij=P(uk=Vj|qk=Di,zk=Wl).该矩阵的设置目的是为了仿真验证本文的方法，该矩阵的不同设置实现方法对本文的逆状态推理方法无影响，本文考虑如下仿真方法.采用如表2 所示的0～9 区间标度对不同干扰样式的有效程度进行定量化干扰效果评估，标度值越大表示干扰样式越有效，干扰方就越可能选取该干扰样式.

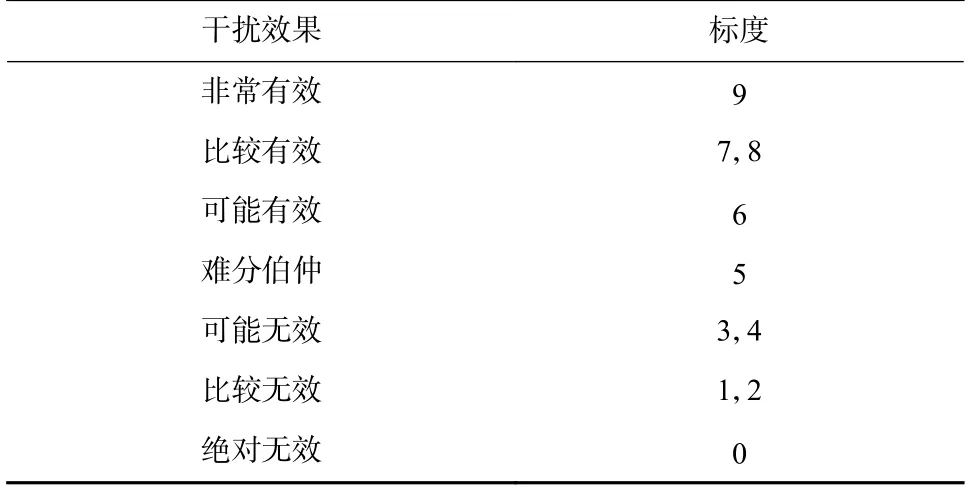
表2 干扰有效性标度定义Tab.2 Jamming effectiveness scale definition

干扰方首先对不同雷达状态、抗干扰措施下，各干扰样式进行有效性标定，记雷达真实状态为Di，抗干扰措施为Wl时，干扰样式Vj的有效性标度为dVj|Wl,Di，选择该干扰样式Vj的概率为

为简化问题，本文假设干扰方认为雷达在当前状态下按照表1 等概率选取对应抗干扰措施，如当雷达处于搜索状态时，雷达抗干扰措施为无措施、频率捷变或旁瓣匿影的概率均为1/3.雷达状态为Di时采取抗干扰措施Wl的概率为pWl|Di，由全概率公式可得Br=[bri j]N×M为

1）搜索状态干扰样式概率.

当雷达处于搜索状态时，干扰有效性如表3 所示.

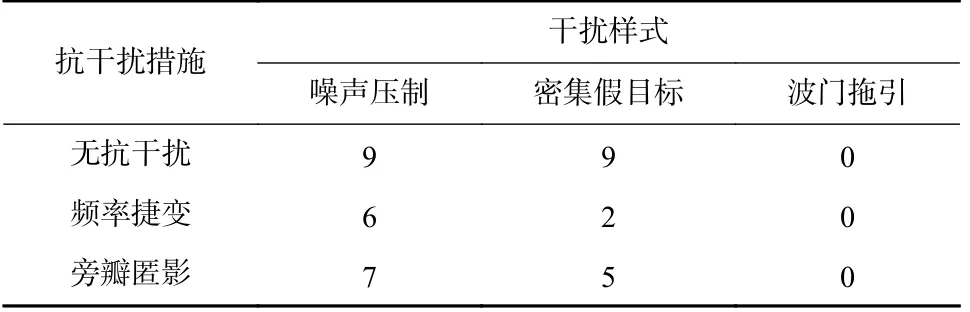
表3 雷达搜索状态下干扰有效性表Tab.3 Jamming effectiveness under radar search mode

根据式(15)、(16)可算得当干扰方认为雷达在搜索状态的条件下，选取噪声压制、密集假目标和波门拖引干扰的概率br11～br13分别为0.611、0.289 和0.

2）确认状态干扰样式概率.

雷达处于确认状态时，使用大能量波束在目标的小区域内照射，可使目标回波信号强度增大.压制类干扰效果比搜索状态时所有降低，而密集假目标干扰效果受影响较小.综上，确认状态的干扰有效性如表4 所示.

表4 雷达确认状态下干扰有效性表Tab.4 Jamming effectiveness in radar confirmation mode

计算可得干扰方状态识别结果为确认状态的条件下，干扰样式选取噪声压制、密集假目标干扰和波门拖引干扰的概率br21～br23分别为0.546、0.454 和0.

3）跟踪/识别状态干扰样式概率.

雷达跟踪和识别状态下的干扰有效性类似，均如表5 所示.

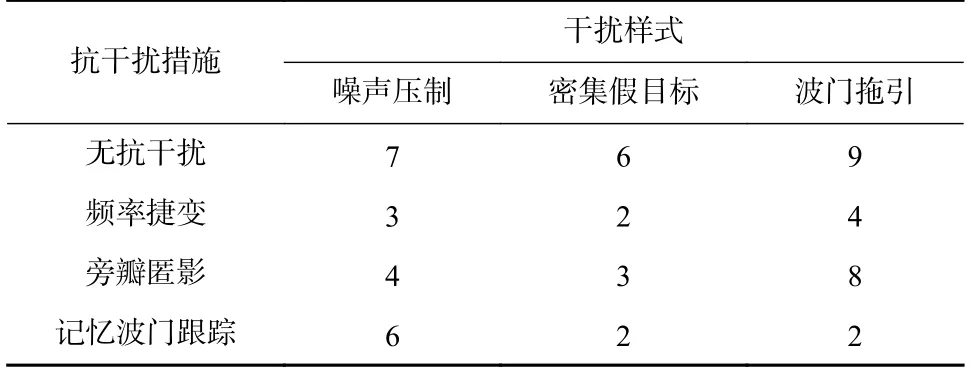
表5 雷达跟踪/识别状态下干扰有效性表Tab.5 Jamming effectiveness in radar tracking / recognition mode

计算可得干扰方状态识别结果为跟踪/识别状态的条件下，干扰样式选取噪声压制、密集假目标干扰和波门拖引干扰的概率分别为0.38、0.224 和0.396.

至此，用于生成干扰方真实干扰样式序列U和雷达方观测干扰样式序列O的真实观测特征概率分布矩阵如下：

3.2.2 真实雷达状态转移概率矩阵生成方法

本节介绍真实雷达状态转移概率矩阵Ar=[ari j]N×N的仿真方法.同3.2.1 节，该矩阵的仿真实现仅为一个实例，不影响本文的方法.根据雷达状态工作原理，有如图4 所示的雷达状态转换图.与用于生成干扰样式序列的真实观测特征概率分布矩阵类似，雷达各工作状态间的转移概率受干扰方干扰和雷达方抗干扰措施间的相互作用影响.

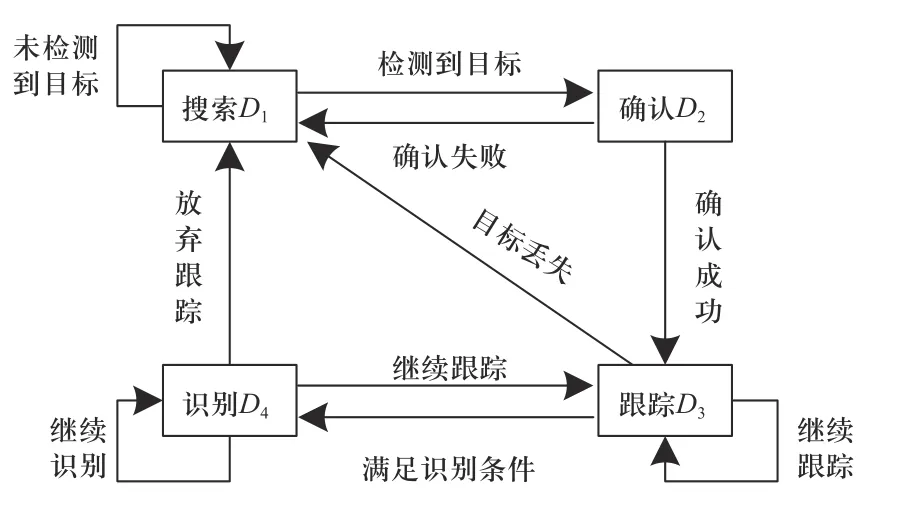
图4 雷达工作状态转移示意图Fig.4 Diagram of radar work mode transition

真实雷达状态转移概率矩阵记为Ar=[ari j]N×N,ari j=P(qk+1=Dj|qk=Di)，则有

与干扰样式序列生成中抗干扰方式设置相似，则上式可写为

其中,P(qk+1=Dj|zk=Wl,ok=Vm,qk=Di)表示观测干扰方干扰样式和雷达方抗干扰措施条件下的雷达状态转移概率.下面以跟踪/识别状态下的状态转移概率为例进行求解.

跟踪和识别状态可转移至搜索、跟踪或识别3种状态，与搜索和确认状态相同，转为搜索状态的概率与干扰有效性标度呈正相关，如式(20)所示.当干扰有效性标度大于5 时，从跟踪/识别状态转移至跟踪状态的概率应大于转移至识别状态的概率，当有效性标度小于5 时，则相反，具体如下:

其中， λ为可调参数，当干扰有效性标度dVj|Wl,Di＞5时，λ=0.6，否则λ=0.4.表6 所示为跟踪/识别状态转移概率.

表6 雷达跟踪/识别状态转移概率表Tab.6 Transition probability in radar tracking / recognition mode

根据雷达方在每种状态下等概率选取表1 中设置的抗干扰措施，并将表6 所示的状态转移概率带入式(19)可得真实雷达状态转移概率矩阵为

3.2.3 干扰方的雷达状态识别结果序列生成方法

干扰方状态识别结果序列Qˆ的生成是在真实雷达状态序列Q的基础上假定干扰方状态识别算法存在一定概率识别错误.即若序列长度为nk，干扰方状态识别准确率为 γ，则干扰方状态估计结果序列和真实雷达状态序列在同一时刻相同的时刻数目为nk·γ，其余时刻的雷达状态被干扰方识别错误为其他状态.

3.3 仿真验证分析

1）HMM 参数初始化算法分析.

本节仿真通过对比逆状态识别准确率 ζ，观察不同参数初始化算法对模型估计准确率的影响，其中ζ为

以前向-后向算法输出的P(O|λ)作为适应度函数，算法迭代次数上限为500，在初始化过程中PSO 和APSO 优化算法的适应度值变化情况如图5 所示.

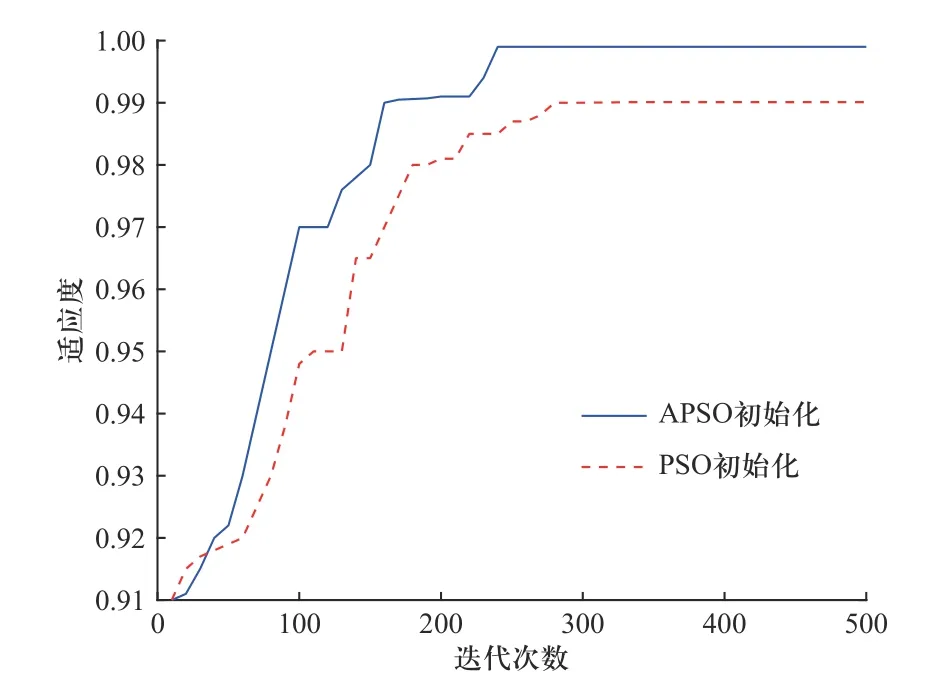
图5 HMM 参数初始化适应度变化曲线图Fig.5 Fitness change curve of HMM parameter initialization

由图5 可知，在基于PSO 和APSO 算法的HMM参数初始化过程中，适应度值随着算法迭代次数增加而增长并逐渐趋于平稳，其达到平稳的时间可表示算法收敛速度.故APSO 算法初始化方法的收敛速度快于PSO 算法，且APSO 算法的适应度值在收敛后更接近于最优值1.综上所述，基于APSO 算法的HMM 参数初始化方法的全局寻优能力更好.随后利用随机参数初始化、PSO 和APSO 算法初始优化后的参数分别作为HMM 模型训练的起始参数，按本文所提方法完成逆状态识别.

训练所需样本数据根据3.2 节所设置矩阵生成.其中生成的干扰方状态识别结果准确率均匀分布在区间70%～100%.仿真产生训练数据序列为50 组，每组序列长度为50.测试样本与训练样本的生成方法相同，序列长度设置为100.对同一测试样本基于不同参数初始化方法进行逆状态识别的准确率如表7 所示.

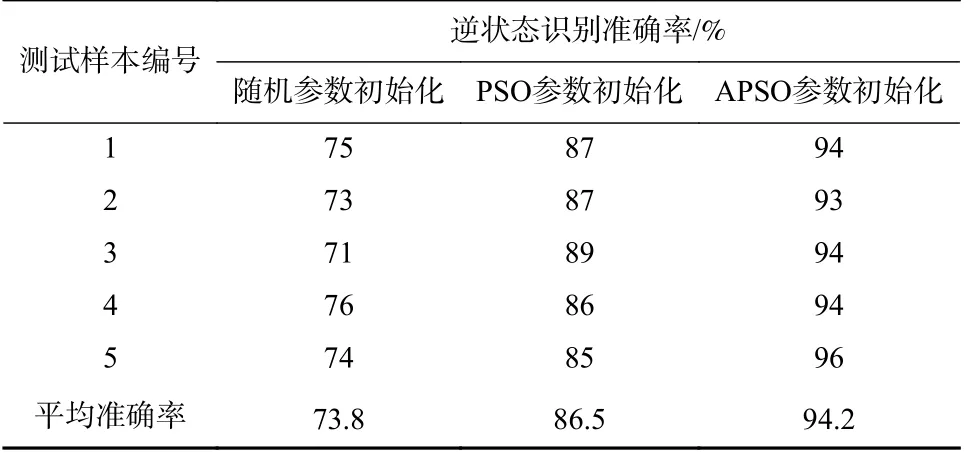
表7 基于不同参数初始化方法的逆状态识别准确率Tab.7 Inverse mode recognition accuracy of different parameter initialization methods

由表7 可知，对于同一测试样本，采取随机参数、PSO 和APSO 算法初始化方法实现的逆状态识别准确率依次提升.且从平均水平角度观察，APSO 算法参数初始化方法也优于另外两种算法.

2）HMM 模型参数优化先验知识分析.

采用较优的APSO 算法进行参数初始化后，为分析HMM 模型参数优化训练对先验知识的需求，利用Baum-Welch 算法模型训练开展HMM 参数优化实验.训练样本集与1）中所用的样本集相同.参数优化完成后，将1）中生成的测试样本输入到训练完成的逆状态识别HMM 模型中进行隐状态估计，逆状态识别准确率随训练样本数变化曲线如图6 所示，图中准确率为对多组测试序列进行逆状态识别后的平均准确率.

图6 不同训练样本数下逆状态识别准确率变化曲线图Fig.6 Inverse mode recognition accuracy change curve under different training sample amounts

由图6 可知，训练样本数在0～15 阶段，随着训练样本数的增加，逆状态识别准确率迅速提升，当训练样本数到达15 时，逆状态识别准确率可达90%以上.当训练样本数达到约25 时，准确率可达到约94%，随着训练样本数进一步增加，逆状态识别准确率趋于平稳.仿真结果表明在先验知识较少的情况下，HMM 模型参数优化训练能够较准确地对干扰方状态识别结果进行估计，且参与HMM 参数优化训练的样本数量越多，雷达方对干扰方多功能雷达工作状态识别的逆向推理准确率越高.

3）HMM 模型逆状态识别稳定性分析.

本验证基于APSO 算法进行HMM 参数初始化，并利用30 组样本训练后的模型参数作为最终的逆状态识别HMM 模型，将干扰方对MFR 状态识别准确率为70%～100%下生成的测试样本分别输入HMM，可得如图7 所示的实验结果.

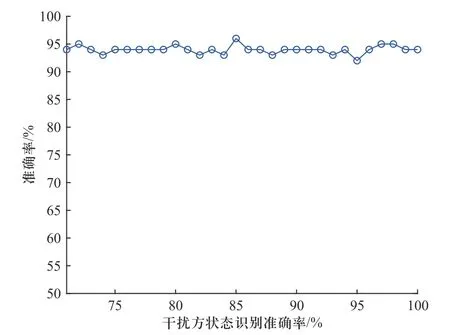
图7 不同干扰方状态识别准确率下逆状态识别准确率变化曲线图Fig.7 Inverse mode recognition accuracy change curve under different jammer mode recognition accuracy rates

由图7 可知，在训练样本数为30 的条件下，当干扰方状态识别准确率变化时，雷达方对干扰方状态识别结果估计的准确率仍稳定在约94%，说明针对MFR 辐射源工作状态识别的逆向推理方法不会受干扰方状态识别准确率的影响，有较好的稳定性.

4 结 论

本文针对对抗场景中提升雷达系统抗干扰能力的实际需求，研究了一种基于隐马尔可夫模型对干扰方的雷达状态识别结果实现逆向推理的方法.雷达方可以利用推理得到的干扰系统内部信号处理节点信息，优化调整雷达工作状态对应的发射波形方案，也可以基于所得HMM 参数，实现对干扰方后续干扰动作的预测，提升系统主动抗干扰的能力.设定雷达对抗场景中的逆状态识别仿真实验，验证了本文任务驱动下模型的可行性及相应算法性能的稳定性.