基于优化支持向量机的土石坝安全监测研究

王 剑，李峰森，周志美

(1.江西省水利科学院，江西 南昌 330029；2.抚州港辉水利建筑有限公司，江西 抚州 334000)

近年来，我国水利事业得到快速发展，尤其近30年来兴建了一批大中型水利工程，如三峡、二滩等水电站[1-2]。这些水利工程在供水、发电及防洪等方面发挥着重要的作用，产生巨大的社会和经济效益[3]。给人们带来巨大便利的同时，水利工程管理不到位也给人民带来了诸多的威胁，如发生溃坝事件，可能对人们群众的生产财产安全带来巨大的损失。因此，水库大坝安全的重要性不容忽视。

对水库大坝的运行进行监测，根据其运行的实际情况和特点设置监测项目，收集大坝运行的监测数据，以此推测大坝的运行规律及存在的安全隐患，便于及时制定相对应的措施，预防安全事件的发生就具有较强的现实意义[4-5]。因此，应建立完善的大坝安全监测体系，以保障大坝的安全运行并充分发挥工程效益。因此，本文基于上述背景，采用优化的支持向量机方法和博弈理论建立科学的土石坝安全监测体系，以期为我国土石坝安全检测工作提供借鉴。

1 构建土石坝安全监测模型

1.1 支持向量机原理

支持向量机算法是基于结构风险最小化思想来解决统计学习问题，主要是通过将原始数据进行映射在高维特征空间来实现对数据的分类和回归。支持向量机算法主要思想是寻找样本距离与最优分类面距离最小的算法。

设存在{(xi，yi)i=1，2，3，…n}，其中x和y分别表示输入和输出数据，n为样本量。其中，输入与输出数据的回归函数为：

f(x)=ωΦ(x)+b

(1)

式中，f(x)—预测值；Φ(x)—映射函数；ω、b—适应系数。

为了方便求解，引入拉格朗日函数，并进行求解，求得最终函数表达式为：

f(x)=ω*Φ(x)+b*

(2)

式中，αi—拉格朗日系数；K(xi，x)—核函数。

由于支持向量机算法具有求解和训练复杂程度比较高，进而选择最小二乘支持向量机算法，具体约束优化模型如下：

(3)

条件为：yi=ωΦ(xi)+b+ei其中，i=1，2，…n

式中，R—损失函数；C—惩罚函数；ei—误差值。

引入拉格朗日函数，并进行求解，得出最终的回归函数表达式：

(4)

1.2 土石坝安全监测模型

土石坝安全监测模型主要包括土石坝位移模型和渗流模型。土石坝位移受诸多因素的影响，最重要的因素包括时效、温度变化及水压，即时效分量、温度分量和水压分量[6-7]。

在位移模型中，水压分量表达式为：

(5)

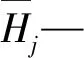
温度分量表达式为：

(6)

式中，t—坝体监测累计天数；t0—自建模资料开始至监测基准日的累计天数；b1i、b2i—温度因子回归系数。

时效分量表达式为：

δθ=c1(θ-θ0)+c2(lim-lnθ0)

(7)

式中，θ—位移监测累计天数除以100；θ0—建模资料开始时累计监测天数除以100；c1、c2—时效因子回归系数。

因此，土石位移统计模型为：δ=δH+δT+δθ。

在渗流模型中，水压分量与时效分量表达式与唯一模型中相同，降雨分量表达式为：

(8)

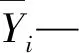
1.3 人工蜂群算法

人工蜂群算法是一种寻找最优资源的随机搜索算法，能够解决数值优化方面的问题，即蜂群采蜜过程就是寻找最优解的过程。

首先，应先确定各参数值及蜜蜂的数量并计算出最初资源适应度值：

uij=uimin+rand(0，1)(ujmax-ujmin)

(9)

式中，rand—区间内随机数；u—变量的边界。

第一阶段为雇佣蜂阶段，在此阶段产生一个食物源：

uij=uij+θij(uij-ukj)

(10)

其中，k和j是随机选取的，θij为区间内的任意数。

第二阶段为跟随蜂阶段，在此阶段选择食物源，并计算适应度值：

(11)

式中，fiti—适应度值，本过程将不断重复，直至得到最优参数。

1.4 基于ABC-SVM模型的建立

其步骤包括4步：

(1)输入数据。包括位移影响因素，如水压、温度和时效；渗流影响因素，如时效、水压和降雨。

(2)数据处理，对数据进行归一化处理，则有：

X′=0.1+0.8×(X-Xmin)/(Xmax-Xmin)

(12)

(3)对支持向量机模型的核函数参数进行优化。

(4)建立基于ABC-SVM的土石坝安全监测模型，将原始数据带入模型。

2 基于博弈理论的土石坝安全性态模糊评价

2.1 拟定监控指标

设定监控模型为：

(13)

则监控指标可以表示为：

(14)

式中，[y]—监控指标边界；x1，x2，…xn—影响监控的环境因素变量；ε—置信带半款。

2.2 建立评判等级

由于目前尚无安全监测指标的统一评判标准，本文根据研究需要以及指标特点，建立了四级评判等级，见表1。

表1 监测指标评判等级

2.3 确定指标权重

本文分别采用层次分析法和熵权法求得指标的主客观权重，并引入博弈理论思想求得综合权重，其步骤如下所示：

(1)假设某大坝监测点有n个，测点权重集为：

W1=(w1，w2，…wn)

(15)

(2)引入系数α1，则综合权重为：

(16)

(3)采用博弈论引入下式求解组合系数α1：

(17)

(4)对上式求解并进行归一化处理，可得：

(18)

(5)则可得出权重最优组合：

(19)

3 安全评价模型应用

3.1 项目概况

江西省宜黄县凤冈惠民水库为烟草行业水源援建项目，位于宜黄县凤冈镇澄源村沙下组，距宜黄县城8.0km，坝址座落在抚河流域临水支流胥坊水上。水库坝址以上控制径流面积17.7km2，水库按50年一遇洪水设计，500年一遇洪水校核，工程等别为Ⅳ等，主要建筑物为4级，次要建筑物为5级，多年平均来水量1822万m3，总库容563.3万m3，兴利库容462.4万m3，正常蓄水位146.0m，校核洪水位为148.20m，死水位为118.0m，是一座以灌溉为主，兼顾供水等综合利用的小(1)型水利枢纽工程，设计灌溉面积0.75万亩，供水人口1.2万人。

为了保证坝体的安全运行，实时监测坝体的状态，该水库设置了完善的监测体系，包括上下游水库水位、降雨量等常规监测项目和内外部变形监测，渗流监测等项目[8-9]。

3.2 基于ABC-SVM模型监测

选取大坝589m高程马道(坝下0+0.39.7m)的D5-7、D9-4、D11-1为位移监测点。以1周为1个监测周期，对3个测点2020年7月1—2022年7月1日共计120组数据进行分析和预测，结果见表2。求得均方差结果见表3。

表2 ABC-SVM模型预测结果 单位：nm

表3 测点预测均方差结果

可以看出，采用ABC-SVM模型进行预测的预测值与实测值非常接近，相对误差较小，预测的平均相对误差低于2%，说明该模型的预测效果较好，在土石坝安全监测中具有适用性和准确性。

3.3 安全性态模糊评价

首先，确定监控指标。对于该水库土石坝下游坝壳选取8个测点，分别为F2、F3、F4、F7、F8、F9、F11、F13。拟定的监控指标见表4。

其次，确定隶属度矩阵。该水库土石坝各测点监控指标评价集模糊隶属度及隶属函数见表5。

通过计算，得出隶属度矩阵：

最后，确定权重。计算得出最优组合权重为：

计算坝体渗流安全等级：

B=W×R=(0.659，0.261，0.061，0.019)

根据计算结果可以看出，该水库土石坝渗流安全评价等级为正常，该结果与其定检报告的结果一致，说明该方法具有准确性和适用性。

4 结语

本文讨论了支持向量机理论在土石坝安全监测中的应用，采用人工蜂群算法对其参数进行了优化，基于博弈理论和主客观赋权法建立土石坝安全性态模糊评价体系，构建了土石坝安全监测系统，不仅为我国土石坝安全监测工作提供了便利，对推动我国水库安全管理起到积极作用，对大坝的安全运行情况能够做出准确的预测，有利于水库安全管理的可持续发展。同时，在对其进行安全性态模糊评价时，采用了较为传统的数学方法拟定监控指标，指标数量不够全面，还应考虑更为科学的方法确定指标，以期得出更为的客观和准确的结果。