低复杂度永磁同步电机双矢量模型预测控制策略
杨狂彪, 陈鼎新, 石 坚
(广州大学 机械与电气工程学院,广东 广州 510006)
0 引言
永磁同步电机因其结构简单,控制便捷,效率高等优点被广泛应用于伺服控制系统中。随着电子器件的快速发展,许多计算量较大的控制算法也逐渐被应用到电机控制领域。由于现代微处理器计算能力的提高,模型预测控制(Model Predictive Control,MPC)已成为磁场定向控制和直接转矩控制的主要竞争对手。MPC的优点是概念直观、动态响应快以及不同约束组合灵活[1-4]。利用电压源逆变器的离散特性,有限控制集MPC(Finite Control Set Model Predictive Control,FCS-MPC)的工作原理是运用适当的电压矢量,使预定义的代价函数最小化[5-7]。传统的FCS-MPC在一个控制周期内采用单个电压矢量。由于有源电压矢量的幅值和相位角是固定的,因此不可避免地降低了电路的工作性能。此外,遍历所有可能的电压矢量也不可避免地增加了计算量[8-9]。
许多研究试图解决FCS-MPC中存在的上述问题。为了提高稳态性能,引入了一种扩展控制集的模型预测转矩控制(Model Predictive Torque Control,MPTC)方法来最小化转矩脉动[10-12],利用有效电压矢量合成的虚拟电压矢量来扩展控制集。另一种通过划分基本扇区来产生更多无谐波的候选电压矢量[13-14],以提高五相永磁电机的运行性能。文献[15-16]中通过增加虚拟电压矢量或候选电压矢量来提高运算性能,但同时也增加了算法的复杂度。文献[17-18]提出了基于占空比的MPC方法,在一个控制周期内,将有效电压矢量与零电压矢量相结合。但由于相位角是固定的,这两种方法都不能达到满意的工作性能。文献[19-20]提出了一种广义的基于两矢量的MPTC方法,该方法通过将电压矢量松弛组合为两个任意电压矢量,获得了较好的工作性能,但由于存在大量不同的电压矢量组合,使得对最优电压矢量的确定十分复杂。
基于以上研究,本文提出了一种双矢量低复杂度模型预测控制策略。此策略避免了遍历所有可能的电压矢量。只有三次代价函数预测计算[21]。根据三个代价函数值的关系确定两个最优有效电压矢量,利用dq轴电压差的作用时间计算方法[22],计算出两个最优有效电压矢量的作用时间。因此,可以降低计算量和电流波动,改善转矩脉动。
1 传统模型预测电流控制
1.1 永磁同步电机数学模型
本文以表贴式永磁同步电机为研究对象,由两电平三相逆变器提供电机驱动电压。在同步旋转坐标系(d-q)下,表贴式永磁同步电机定子电流的交直轴分量分别为
(1)
式中:id、iq分别为电机d、q轴电流分量;Ld、Lq分别为电机d、q轴电感;ud、uq分别为电机d、q轴电压分量;Rs为电机定子电阻;ωe为转子的电角速度;ψf为永磁体磁链。
为计算下一个采样时刻的电流预测值,用欧拉法可近似得到离散d、q轴预测电流分别为
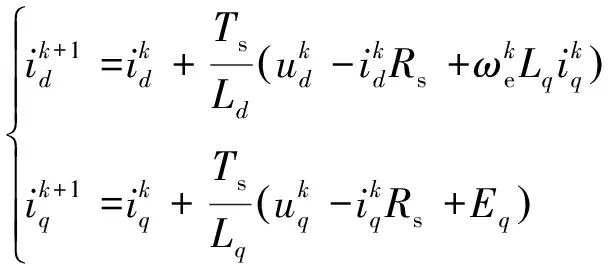
(2)
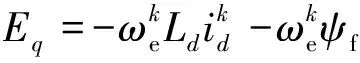
(3)

1.2 占空比模型预测电流控制
占空比模型预测电流控制是在传统有限控制集模型预测电流控制的基础上引入占空比控制,即计算被代价函数选择出的最优电压矢量的作用时间,让最优电压矢量只作用采样周期的一部分,其余时间由零电压矢量作用。
1.3 双矢量模型预测电流控制
双矢量模型预测电流控制是在传统有限集模型预测电流控制选择出最优电压矢量uopt1的基础上,再进行一次电压矢量选择来确定第2个最优电压矢量uopt2。在选择uopt2时,将最优电压矢量uopt1和6种有效电压矢量分别组合,采用q轴电流无差拍,计算出预先分配每个组合中两个电压矢量的作用时间,根据式(2)得到预测电流,然后依次代入式(4),选择出代价函数值最小的组合,即可确定第2个最优电压矢量uopt2。
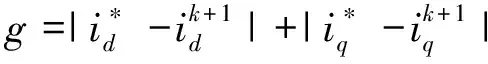
(4)
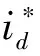
2 低复杂度双矢量模型预测电压控制
传统占空比模型预测电流控制和双矢量模型预测电流控制的代价函数均以电流误差为基准,需经式(4)将电压矢量转化为d、q轴电流,然后代入代价函数,计算量较大。本文所提的低复杂度双矢量模型预测控制策略是在双矢量控制原理的基础上,将式(2)和(3)代入式(4)中,得到以电压误差为基准的代价函数,如式(5)所示。直接用候选的电压矢量与参考电压矢量进行比较,减小了计算量,同时通过高效电压矢量快速选择出所需的两个相邻最优有效电压矢量,无需遍历所有电压矢量,然后引入dq轴电压差的作用时间计算方法,计算最优有效电压矢量作用时间,去控制合成期望电压矢量的幅值大小,以降低计算量。
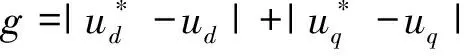
(5)
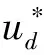
所提的低复杂度双矢量模型预测控制策略结构框图如图1所示。
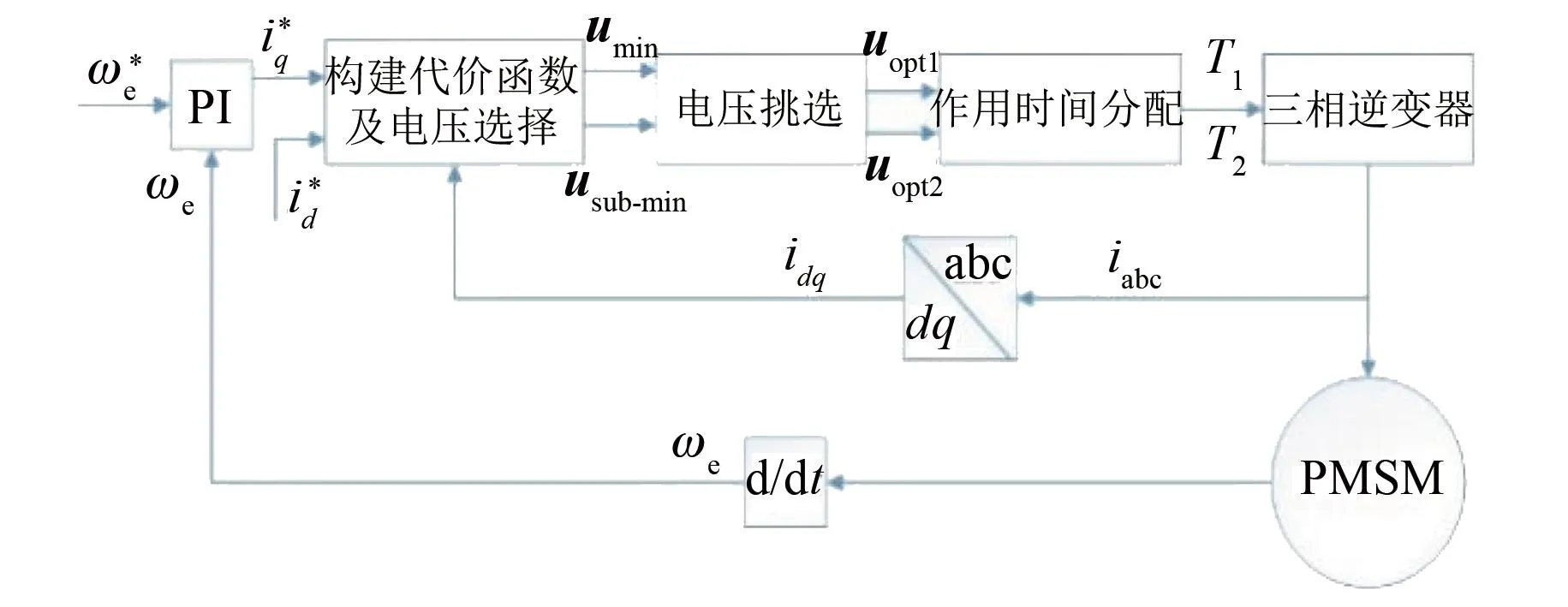
图1 系统控制框图
2.1 最优有效电压矢量的选择
最优有效电压矢量的选择方法无需遍历所有电压矢量,而仅需遍历三个矢量,分别是u1=[1 0 0]、u3=[0 1 0]和u5=[0 0 1]。通过遍历这三个电压得到这三个电压矢量对应的代价函数值g1、g3和g5。根据代价函数g1、g3和g5的大小关系选出代价函数值最小的对应电压矢量umin和代价函数值次小的对应电压矢量usub-min。umin和usub-min的选定如表1所示。

表1 umin和usub-min的选定
两个相邻最优有效电压矢量uopt1和uopt2是由umin和usub-min的位置决定的。uopt1和uopt2的选定方法如表2所示。
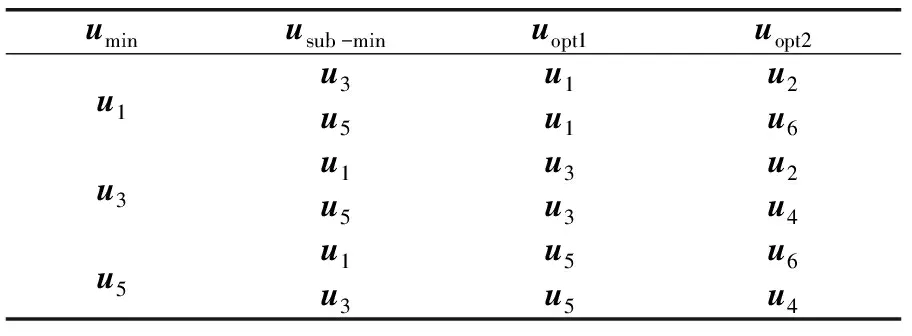
表2 相邻最优电压选定方法
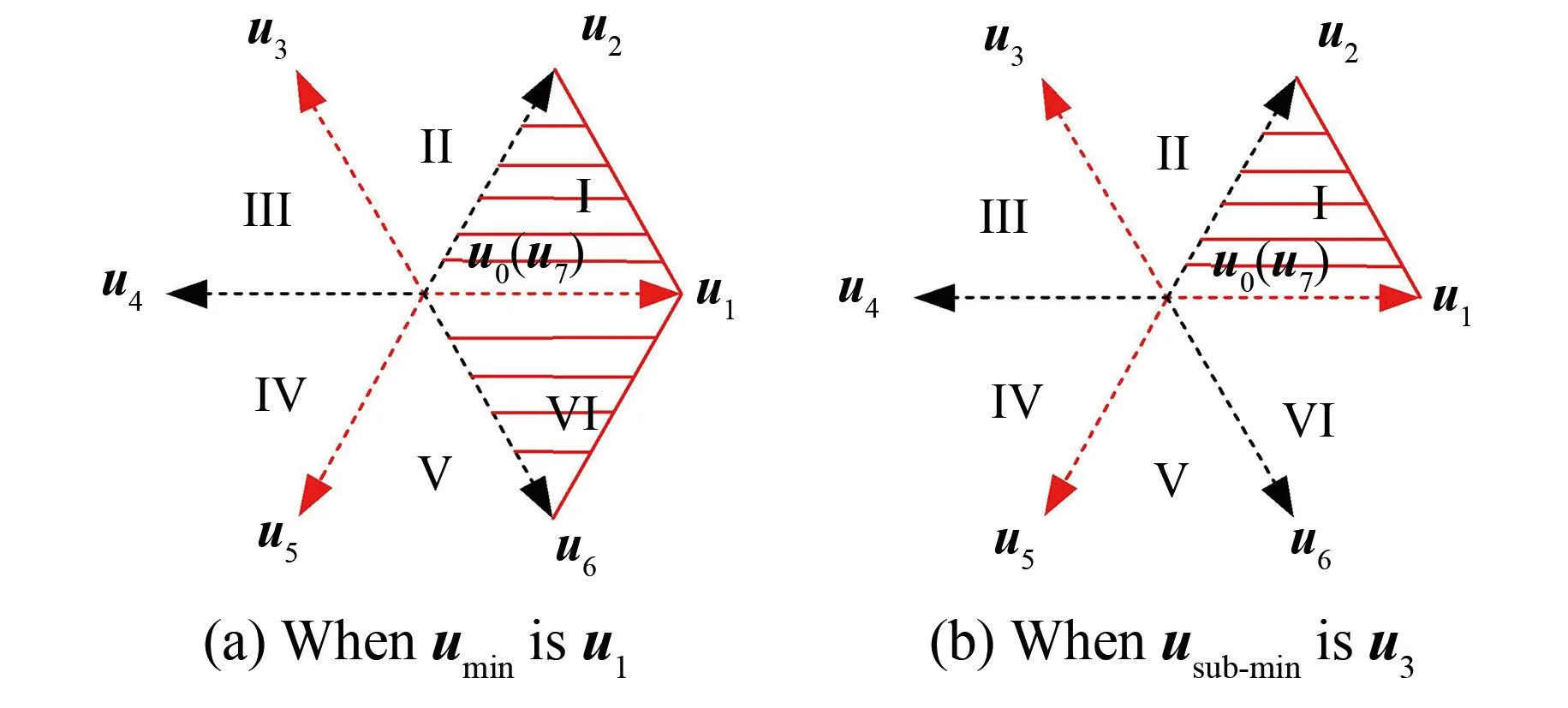
两个最优有效电压矢量的选择过程如图2所示。假定umin是u1,则最优化的期望电压在扇区1或者扇区6中,uopt1就等于u1;uopt2的值取决于usub-min的位置,如果u3是usub-min,那么uopt2就等于u2;如果u5是usub-min,那么uopt2就等于u6。
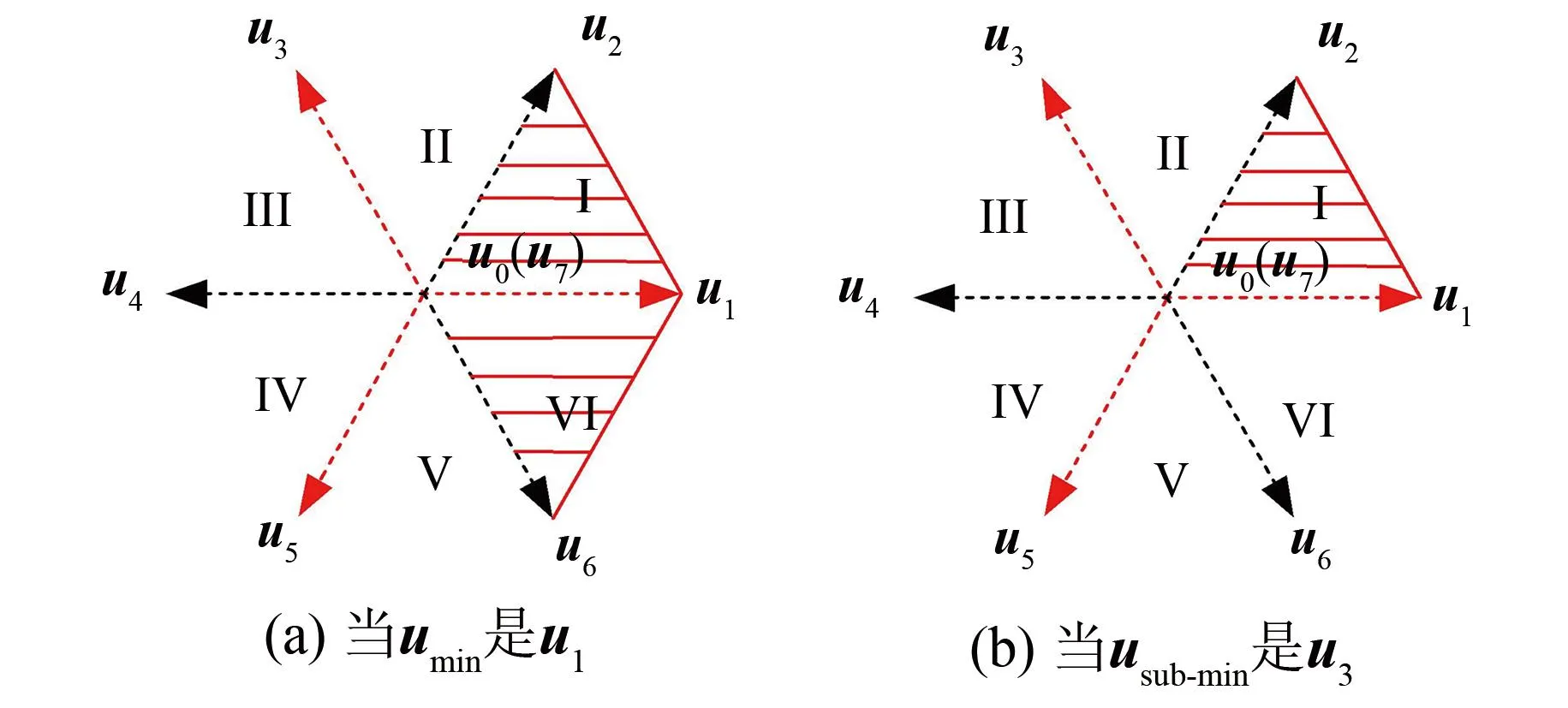
图2 电压矢量选择过程
两个相邻最优有效电压矢量uopt1和uopt2经过三次代价函数预测计算挑选得到,可以高效地选择相邻电压矢量的所有组合,减小计算量。
2.2 电压矢量作用时间的计算
在计算电压矢量的作用时间时,要求作用时间必须恒为正值,所选取的最优有效电压矢量在一个周期内实际作用效果如图3所示。

图3 有效电压矢量作用图
在理想最优有效电压作用下,d、q轴的电压误差为零,但实际应用中,电压误差不可能为零。因此每个最优有效电压矢量产生的d、q轴电压误差分别为
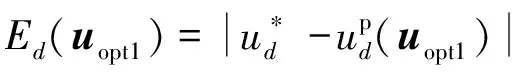
(6)
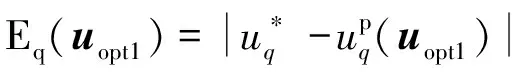
(7)
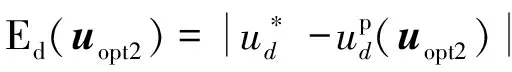
(8)

(9)
综合考虑d、q轴的电压误差,可建立计算持续时间的方程如下:
T1[Ed(uopt1)+Eq(uopt1)]+
T2[Ed(uopt2)+Eq(uopt2)]=δ
(10)
T1+T2=Ts
(11)
式中:T1和T2分别为uopt1和uopt2的持续时间;δ是一个变量,表示一个控制周期后的d、q轴的电压误差。
联立式(10)和(11),解得
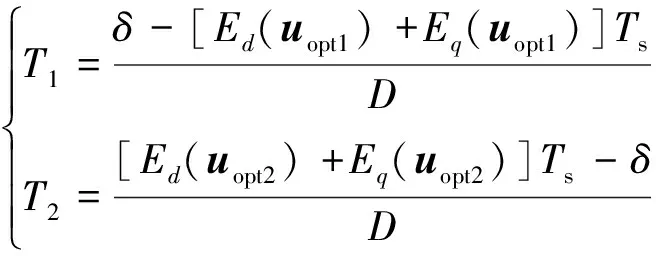
(12)
式中:D=Ed(uopt1)+Eq(uopt1)-Ed(uopt2)-Eq(uopt2)。
可见T1和T2的大小与变量δ有关,所以为了保证T1和T2的值同时大于零,必须对δ的大小进行分析。由于中间变量D的表达式中不包含变量δ,所以可从中间变量D的表达式入手,分两种情况讨论。
第一种是D大于零的情况,此时满足:Ed(uopt1)+Eq(uopt1)>Ed(uopt2)+Eq(uopt2)。
此时若要保证T1和T2都大于零,则δ的取值范围为
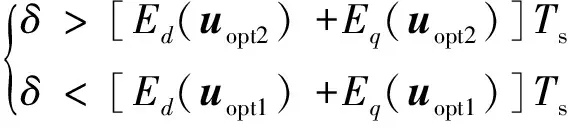
(13)
第二种是D小于零的情况,此时满足:Ed(uopt1)+Eq(uopt1) 此时若要保证T1和T2都大于零,则δ的取值范围为 (14) 综上,δ的取值范围为 gminTs<δ (15) 式中:gmin和gmax分别为两个最优电压矢量对应的电压差型代价函数的最小值和最大值。 选择合适的δ之后,电压矢量的持续时间就恒大于零,经多次验证,变量δ取值为 (16) 式中:gopt1和gopt2分别为最优电压矢量uopt1和uopt2对应的电压差型代价函数值。 根据上述控制原理,对占空比、双矢量以及低复杂度双矢量三种控制策略在矢量数目、预测次数、电压矢量选择范围及矢量作用时间计算方法等方面进行对比分析,其结果如表3所示。 从表3中可以看出占空比控制策略需要经过6次在线电流预测,在6个有效电压矢量中选择出一个最优电压矢量,但选择的电压矢量只能在基本电压矢量方向上,有局限性。而双矢量控制策略需要在线进行12次预测,在选择出第一个最优电压矢量uopt1的基础上,再进行一次电压矢量选择来确定第2个最优电压矢量uopt2,虽然电压矢量选择时方向和幅值是任意的,但两个有效矢量作用时间的计算是采用q轴电流无差拍方法,计算量较大。低复杂度双矢量策略选择电压矢量方向任意,幅值任意,相比于双矢量控制策略,在线预测次数仅为3次,即可选择出2个最优有效电压矢量,同时代价函数采用以电压误差为基准,不需要进行电流预测,并采用基于dq轴电压误差方法计算电压矢量作用时间,极大地减小了计算量。 表3 三种控制策略比较 为了验证本文所提策略的有效性,基于Matlab/Simulink平台构建了永磁同步电机低复杂度双矢量模型预测控制系统的离散仿真模型。分别对占空比控制策略、双矢量控制策略和本文所提的低复杂度双矢量控制策略,在空载起动、突加负载运行以及转速突增三种情况下进行仿真。仿真中,采样频率均为10 kHz,采用定步长计算,使用ode4求解算法。使用的永磁同步电机的参数如表4所示。 表4 永磁同步电机参数 对仿真系统做空载起动时的测试。永磁同步电机以给定转速为800 r/min空载起动,对动态响应速度,dq轴电流波动进行分析。空载起动到达稳定后,三种控制策略下对应的id和iq电流仿真结果分别如图4和图5所示。 图4 转速为800 r/min空载起动时三种控制策略下id电流波形 从图4可知,占空比策略下id上下波形值为1.150 854 A,双矢量控制策略下为0.951 523 A,而低复杂度双矢量控制策略下为0.500 706 A。相较于占空比策略,双矢量策略电流波动分别减少了56.492%,47.378%。 由图5可知,占空比控制策略下iq上下波形值为0.830 328 A,双矢量控制策略下为0.658 095 A,而所提的低复杂度双矢量控制策略下为0.639 641 A。相较于占空比策略,双矢量策略电流波动分别减少了20.742%,2.804%。 图5 转速为800 r/min空载起动时三种控制策略下iq电流波形 电机在给定转速为800 r/min空载起动时,对a相定子电流进行FFT分析,如图6所示。结果表明,频率相同时,相较于广义双矢量控制策略和占空比控制策略,所提的低复杂度控制策略下的直轴电流波动确实有所降低。 进一步对仿真系统做突加负载测试。永磁同步电机设定转速为800 r/min,0.02秒时突加5 N·m的负载,对电磁转矩Te、转速Nr进行分析,其结果分别如图7和8所示。 图6 转速为800 r/min空载起动时三种控制策略下a相定子电流与FFT分析 图7 转速为800 r/min突加负载时三种控制策略下的Te 图8 转速为800 r/min突加负载时三种控制策略下的Nr 由图7可知,在突加负载情况下,低复杂度双矢量控制策略下转矩脉动为11.16%;双矢量策略下转矩脉动为15.53%;占空比策略转矩脉动为18.50%。可见,低复杂度双矢量策略能够更好地改善系统稳定性,降低转矩脉动。 由图8可知,相比于占空比控制和双矢量控制,低复杂度双矢量控制策略能更快达到稳定状态,且稳态转速波动较小。 对仿真系统做给定转速突增测试。永磁同步电机初始转速为400 r/min,0.02 s时突增为800 r/min,对q轴电流波动进行分析,电流仿真结果如图9所示。 图9 0.02 s转速突增为800 r/min时三种控制策略下的iq电流波形 由图9可见,转速在0.02 s从400 r/min突增为800 r/min时,占空比控制策略下iq上下波形值为0.949 884 A,双矢量控制策略下其为0.587 871 A,而低复杂度双矢量控制策略下仅为0.539 854 A。相较于占空比控制策略,双矢量策略电流波动分别减少了43.166%和8.167%。 同时,对仿真程序运行时间进行对比分析。在同等设备,同等情况下电机设定800 r/min空载起动时三种控制策略下的仿真程序运行时间如表5所示。可见在本文所提的低复杂度双矢量控制策略下,由于程序优化,其运行时间略大于占空比控制策略。但相较于传统双矢量控制策略运行时间节约很多。 表5 三种控制策略下的仿真程序运行时间 本文提出了一种低复杂度双矢量模型预测电压控制策略。该策略以电压误差为基准,通过三次代价函数计算,选择出两个相邻最优有效电压矢量。并引入dq轴电压差作用时间计算方法,计算最优有效电压矢量作用时间,以降低计算量。仿真结果表明,相较于占空比策略和传统双矢量策略,所提策略可有效减小电流波动和转矩脉动,提高系统稳态性能,证明了所提策略的优越性。 Low Complexity Dual Vector Model Predictive Control Strategy for Permanent Magnet Synchronous Motor YANG Kuangbiao, CHEN Dingxin, SHI Jian* (School of Mechanical and Electrical Engineering, Guangzhou University, Guangzhou 510006, China) Keywords: permanent magnet synchronous motor; model predictive control; cost function; low complexity;dqaxis voltage difference In order to solve the problems of large computation and current fluctuations in the model predictive current control of permanent magnet synchronous motor, a low complexity dual vector model predictive voltage control strategy is proposed. This method predicts and evaluates three non-adjacent effective voltage vectors only through cost functions, and two adjacent optimal effective voltage vectors can be determined accurately and quickly based on the relationship between the values of three cost functions, without traversing all the voltage vectors. The selection of two optimal effective voltage vectors is shown in Fig.1. Assuminguminisu1, the best expected voltage is in sector 1 or sector 6, whereuopt1is equal tou1, and the value ofuopt2depends on the position ofusub-min. Ifu3isusub-min, thenuopt2is equal tou2; Ifu5isusub-min, thenuopt2is equal tou6. The optimal and effective voltage vector selection can reduce the prediction calculation, and thedqaxis voltage difference action time calculation method is introduced to calculate the optimal effective voltage vector action time in order to reduce the calculation. A permanent magnet synchronous motor driven by a two-level three-phase inverter is simulated using the Matlab/Simulink simulation software platform in this paper. Through simulation analysis, compared to the duty cycle strategy and the traditional dual vector model predictive current control strategy, the proposed low complexity permanent magnet synchronous motor control strategy can effectively reduce the computational complexity and current fluctuation and improve the torque ripple on the basis of ensuring the steady-state and dynamic performance of the system. Although this method requires additional running time during the optimization process compared to the duty cycle strategy, considering the improvement of system performance, the additional time is acceptable. Simulation analysis proves the superiority of this method. Fig.1 Voltage vector selection process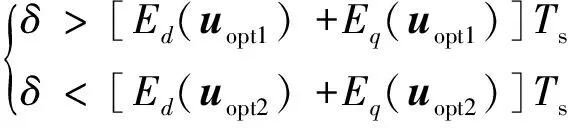

2.3 三种控制策略对比分析

3 仿真分析

4 结语